Похожие презентации:
Дедуктивний умовивід
1. Дедуктивний умовивід
2. ПЛАН
1. Категоричний силогізм.2. Умовиводи зі складними судженнями.
3. 1. Категоричний силогізм.
Силогізм (syllogismos) перекладається згрецької як збірка логосів, тобто
суджень.
Категоричний силогізм – це дедуктивне
міркування, в якому з двох категоричних
суджень виводиться третє - нове
категоричне судження.
4. 1. Категоричний силогізм. Структура категоричного силогізму
Терміни силогізму – це поняття Засновки – ісходні(S, P, М), що входять в засновки категоричні судження, з яких
та висновок силогізму
виводиться нове судження
Більший термін (Р) - предикат
висновку
Середній термін (М) - поєднує
засновки, але відсутній у
висновку
Менший термін (S) - суб’єкт
висновку
Більший засновок – це
судження, в яке входить
більший термін
Менший засновок - це
судження, в яке входить
менший термін
5. 1. Категоричний силогізм.
Категоричний силогізм – це умовивід про відношеннядвох крайніх термінів на підставі їх відношення до
середнього терміну.
Правильність силогізму не залежить від його
змісту, а залежить лише від його форми.
Наприклад:
Будь-який злочин – суспільно-небезпечне діяння.
Пограбування – це злочин.
Отже, пограбування – це суспільно-небезпечне
діяння.
6. 1. Категоричний силогізм. АКСІОМА КАТЕГОРИЧНОГО СИЛОГІЗМУ
Все, що стверджується або заперечуєтьсяпро весь клас предметів, стверджується або
заперечується щодо кожного предмета
даного класу (екстенсіональне
формулювання).
Ознака ознаки речі є ознакою самої речі; те,
що суперечить ознаці речі, суперечить
самій речі (інтенсіональне формулювання).
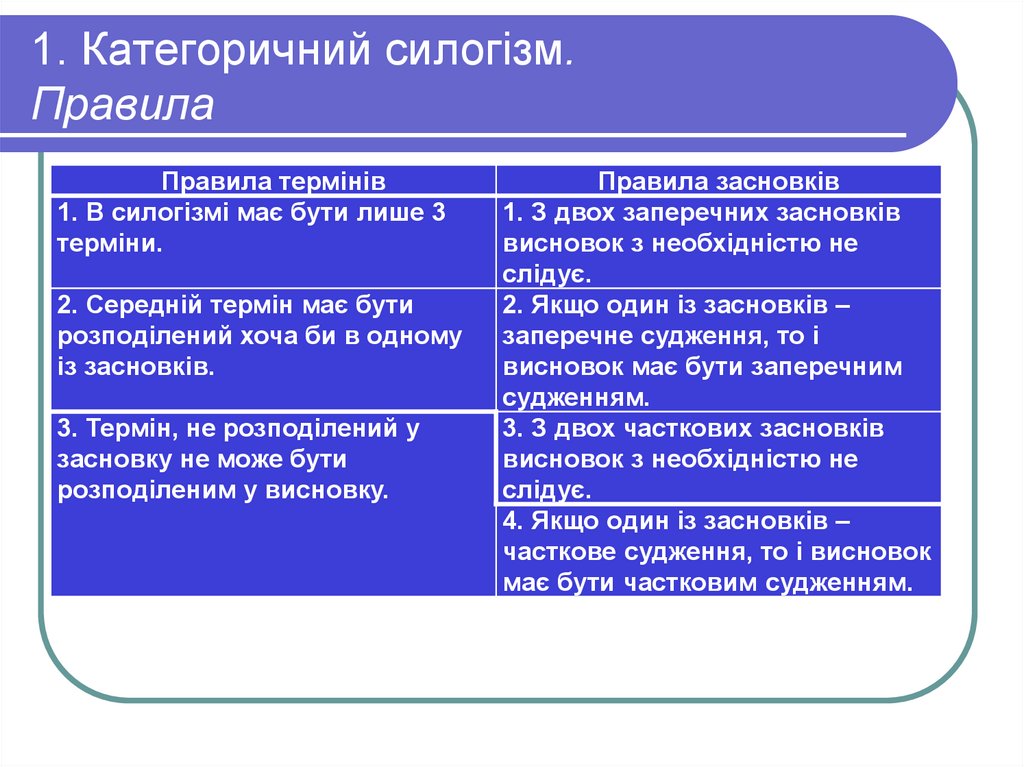
7. 1. Категоричний силогізм. Правила
Правила термінів1. В силогізмі має бути лише 3
терміни.
2. Середній термін має бути
розподілений хоча би в одному
із засновків.
3. Термін, не розподілений у
засновку не може бути
розподіленим у висновку.
Правила засновків
1. З двох заперечних засновків
висновок з необхідністю не
слідує.
2. Якщо один із засновків –
заперечне судження, то і
висновок має бути заперечним
судженням.
3. З двох часткових засновків
висновок з необхідністю не
слідує.
4. Якщо один із засновків –
часткове судження, то і висновок
має бути частковим судженням.
8. 1. Категоричний силогізм. ФІГУРИ ТА МОДУСИ КАТЕГОРИЧНОГО СИЛОГІЗМУ
Фігури силогізму – Модусице різновиди
силогізму - це
силогізму, що
різновиди
відрізняються
силогізму, що
положенням
відрізняються
середнього
кількістю та
терміну в
якістю засновків
засновках
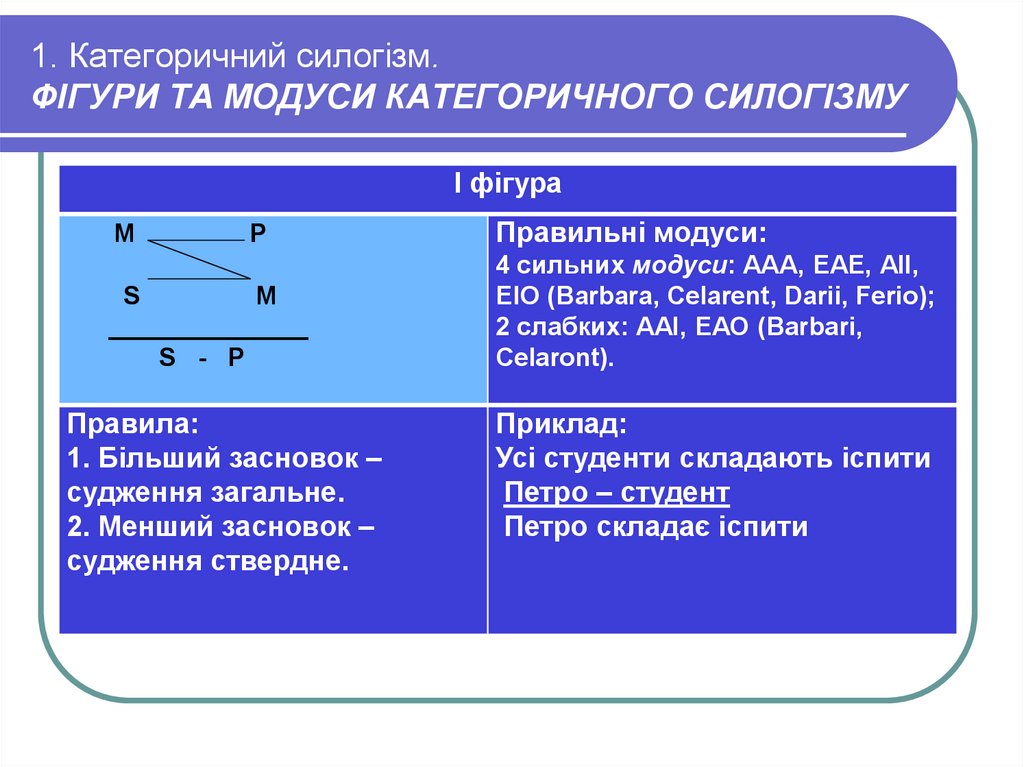
9. 1. Категоричний силогізм. ФІГУРИ ТА МОДУСИ КАТЕГОРИЧНОГО СИЛОГІЗМУ
І фігураM
P
S
M
______________
S - P
Правила:
1. Більший засновок –
судження загальне.
2. Менший засновок –
судження ствердне.
Правильні модуси:
4 сильних модуси: ААА, ЕАЕ, АІІ,
ЕІО (Barbara, Celarent, Darii, Ferio);
2 слабких: ААІ, ЕАО (Barbari,
Celaront).
Приклад:
Усі студенти складають іспити
Петро – студент
Петро складає іспити
10. 1. Категоричний силогізм. ФІГУРИ ТА МОДУСИ КАТЕГОРИЧНОГО СИЛОГІЗМУ
ІІ фігураР
М
S
M
______________
S - P
Правильні модуси:
4 сильних: EAE, AEE, EIO, AOO
(Сesare, Camestres, Festino,
Baroco);
2 слабких: EAO, AEO (Cesarо,
Camestrо).
Правила:
Приклад:
1. Більший засновок –
Усі студенти складають іспити
судження загальне.
Петро не складає іспити
2. Один із засновків – судження Петро – не студент
заперечне.
11. 1. Категоричний силогізм. ФІГУРИ ТА МОДУСИ КАТЕГОРИЧНОГО СИЛОГІЗМУ
ІІІ фігураМ
Р
М
S
______________
S - P
Правила:
1. Менший засновок –
судження ствердне.
2. Висновок - судження
часткове.
Правильні модуси:
АAІ, ІАІ, АІI, ЕАО, ОАО, ЕІО (Darapti,
Disamis, Datisi, Felapton, Bocardo,
Ferison)
Приклад:
Усі студенти складають іспити
Деякі студенти - майстри спорту
Деякі майстри спорту складають
іспити
12. 1. Категоричний силогізм. ФІГУРИ ТА МОДУСИ КАТЕГОРИЧНОГО СИЛОГІЗМУ
ІV фігураP
M
М
S
______________
S - P
Правила:
Правильні модуси:
5 сильних: AAI, AEE, IAI, EAO, EIO
(Bramantip, Camenes, Dimaris,
Fesapo, Fresison)
1 слабкий: AEO (Сamenоs).
Приклад:
1. Якщо більший засновок −
Усі студенти складають іспити
судження ствердне, то менший −
Дехто з тих, хто складає
загальне.
іспити – майстри спорту
2. Якщо один з засновків −
Деякі майстри спорту є
судження заперечне, то більший −
студентами
загальне.
Запам’ятайте, що по четвертій фігурі
ніколи не буде загальноствердних
суджень у висновку.
13. Приклади завдань з ЗНО
Прочитайте наведені тексти в формі тестовихзавдань, з'ясуйте їх структуру, проаналізуйте
відповіді до кожного тесту й обгрунтуйте серед
наведених правильну.
1. Методист: Жоден зі студентів, які вивчають право,
не вивчає математики, проте деякі студенти, які
вивчають математику, вивчають мистецтво. Окрім
того, жоден студент, який вивчає літературу, не
вивчає математику.
Яке з наведених нижче суджень логічно випливає з
наведеного твердження?
14. Приклади завдань з ЗНО
А Деякі студенти вивчають одночасно і мистецтво, іправо.
Б Є студенти, які вивчають мистецтво, проте не
вивчають права.
В Жоден зі студентів, які вивчають літературу, не
вивчає мистецтва.
Г Є студенти, які вивчають літературу й не вивчають
права.
Д Жоден зі студентів, які вивчають літературу, не
вивчає права.
15. Приклади завдань з ЗНО
2. Біолог: Для характеристики котів прийняті категорії«Добрий мисливець» і «Поганий мисливець». Добрий
мисливець може впіймати жертву вагою до половини
ваги власного тіла. Усі добрі мисливці мають високий
МЖ-показник (МЖ–показник дорівнює відношенню
маси мускулів до маси жиру). Більшість диких котів є
добрими мисливцями, разом з тим деякі домашні коти
також є добрими мисливцями.
Якщо наведені вище твердження істинні, яке з
наведених нижче тверджень також має бути
істинним?
16. Приклади завдань з ЗНО
А Усі коти з високим МЖ-показником можуть пійматижертву вагою до половини ваги власного тіла.
Б Усі коти з високим МЖ-показником є добрими
мисливцями.
В Порівняно з дикими котами менша кількість
домашніх котів має високий МЖ-показник.
Г Усі коти, які є поганимимисливцями, мають низький
МЖ-показник.
Д Деякі коти з високим МЖ-показником є домашніми.
17. 2. Умовиводи зі складними судженнями. Суто умовний силогізм
Простим умовним (суто умовним) силогізмомназивається дедуктивний умовивід, засновки і
висновок якого є умовними (імплікативними)
судженнями. Структура такого силогізму:
а b
b с
а с
Висновок у чисто умовному силогізмі ґрунтується на
правилі: наслідок наслідку є наслідком підстави.
((а → b) (b → c)) → (a → c) в класичному розумінні є
законом логіки.
18. 2. Умовиводи зі складними судженнями. Суто умовний силогізм
Наприклад:Якщо громадянин дотимується закону, то він –
законослухняний.
Якщо він законослухняний, то він має
правосвідомість.
Якщо громадянин дотримується закону, то він має
правосвідомість.
19. Приклади завдань з ЗНО
Не може бути індивідуальної свободибез верховенства закону, оскільки не
може бути індивідуальної свободи без
соціальної справедливості, як і не може
бути високої якості життя без соціальної
справедливості.
За умови істинності якого з поданих
нижче тверджень наведена вище теза є
логічно обґрунтованою?
20. Приклади завдань з ЗНО
А Не може бути соціальної справедливостібез верховенства закону.
Б Не може бути високої якості життя без
верховенства закону.
В Соціальна справедливість можлива тільки
за панування індивідуальної свободи.
Г Не може бути верховенства закону без
індивідуальної свободи.
Д Не може бути верховенства закону без
соціальної справедливості.
21. 2. Умовиводи зі складними судженнями. Умовно-категоричний силогізм
Умовно-категоричним силогізмом називаєтьсядедуктивний умовивід, у якому один з засновків є
судженням умовним, а другий засновок і висновок
– категоричними.
Розрізнюють два модуси умовно-категоричного
силогізму: ствердний (modus ponens) та
заперечний (modus tollens).
22. 2. Умовиводи зі складними судженнями. Умовно-категоричний силогізм
В структурі modus’а ponens перший засновок – це умовнесудження, в другому засновку стверджується причина, а у
висновку стверджується наслідок першого засновку.
Схема:
а b, a
b
Наприклад:
Якщо позов подано неповнолітньою особою (а), то суд залишає
позов без розгляду (b).
Позов подано неповнолітньою особою (a).
Отже, суд залишив позов без розгляду (b).
23. 2. Умовиводи зі складними судженнями. Умовно-категоричний силогізм
При наявності заперечних суджень вструктурі умовиводу порядок
ствердження (від підстави до наслідку)
не змінюється.
Схеми:
а b, а
а b, а
а b, а
b
b
b
24. 2. Умовиводи зі складними судженнями. Умовно-категоричний силогізм
В структурі modus’a tollens перший засновок – це імплікативнесудження, в другому засновку заперечується наслідок
імплікативного засновку, а у висновку заперечується його
підстава.
Схема:
a → b, b
a
Наприклад:
Якщо позов подано неповнолітньою особою (а), то суд залишає
позов без
розгляду (b).
Позов не залишили без розгляду ( b).
Отже, позов не був поданий неповнолітньою особою ( а).
25. 2. Умовиводи зі складними судженнями. Умовно-категоричний силогізм
Загальне правило умовно-категоричного силогізму:Ствердження імплікації відбувається від підстави до
наслідку, але не навпаки. Заперечення імплікації
відбувається від наслідку до підстави, але не
навпаки.
Порушення цього правила призведе до логічної
помилки.
В умовно-категоричному силогізмі можлива помилка,
яка називаться псевдопричинний зв’язок. Якщо події
ідуть одна за одною в часі, то може здаватися, що
вони пов’язані причинно-наслідковою зв’язкою, але це
не завжди так.
26. 2. Умовиводи зі складними судженнями. Еквівалентно-категоричний силогізм
Еквівалентно-категоричний силогізм – це вид складногосилогізму, в якому перший засновок є еквівалентним судженням,
а другий засновок і висновок є категоричними.
Еквівалентно-категоричний силогізм має два ствердні і два
заперечні модуси. Порядок ствердження і порядок заперечення
може бути вільним – або від підстави до наслідку, або від
наслідку до підстави.
Схеми ствердних модусів:
1) a b, a
2) a b, b
b
a
Наявність заперечних суджень у структурі даного силогізму не
впливає на порядок підтвердження.
27. 2. Умовиводи зі складними судженнями. Еквівалентно-категоричний силогізм
Приклади:1) Якщо і тільки якщо людина не має ознак
життя ( a), то вона померла (b).
П. не має ознак життя ( a).
Отже, П. помер (b).
2) Якщо і тільки якщо людина не має ознак
життя ( a), то вона померла (b).
П. помер (b).
Отже, П. не має ознак життя ( a).
28. 2. Умовиводи зі складними судженнями. Еквівалентно-категоричний силогізм
Схеми заперечних модусів:1) a b, a
2) a b, b
b
a
Наявність заперечних суджень у структурі даного силогізму не
впливає на порядок заперечення.
Приклади:
1) Якщо і тільки якщо людина не має ознак життя ( a), то вона
померла (b).
П. має ознаки життя (a).
Отже, П. не помер ( b).
2) Якщо і тільки якщо людина не має ознак життя ( a), то вона
померла (b).
П. не помер ( b).
Отже, П. має ознаки життя (a).
29. 2. Умовиводи зі складними судженнями. Розділово-категоричний силогізм
Назва «розділово-категоричний» тежвідбиває склад цього дедуктивного
умовиводу: перший засновок −
судження розділове, другий засновок і
висновок – судження категоричні.
Розділово-категоричний силогізм має
два правильних модуси: стверднозаперечний і заперечно-ствердний.
30. 2. Умовиводи зі складними судженнями. Розділово-категоричний силогізм
Модус ствердно-заперечний (modus ponendo tollens, MPT)будується від ствердження одного диз’юнкта в другому засновку
до заперечення інших диз’юнктів у висновку.
Схема:
a b. a
b
Наприклад:
Завтра я або залишуся в Харкові (a), або поїду в Полтаву о 8-й
годині ранку (b).
Я вирішив залишитись у Харкові (а).
Отже, невірно, що я поїду в Полтаву о 8-й годині ранку ( b).
31. 2. Умовиводи зі складними судженнями. Розділово-категоричний силогізм
Модус заперечно-ствердний (modus tollendo ponens, МТР)будується від заперечення диз’юнктів у другому засновку до
ствердження одного з диз’юнктів у висновку.
Схема:
a b. a
b
Наприклад:
Завтра я або залишуся в Харкові (a), або поїду в Полтаву о 8-й
годині ранку (b).
Я вирішив не залишатись у Харкові ( а).
Отже, я поїду в Полтаву о 8-й годині ранку (b).
32. 2. Умовиводи зі складними судженнями. Розділово-категоричний силогізм
Правила розділово-категоричного силогізму:1. Розділове судження повинно бути сильною
диз’юнкцією.
2. У розділовому судженні повинні бути
враховані всі можливі диз`юнкти.
При порушенні правил розділовокатегоричного силогізму виникають логічні
помилки.
33. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Умовно-розділовий силогізм містить упершому засновку судження умовне, а в
другому — судження розділове (диз’юнкція).
Умовно-розділовий силогізм називають
лемою (від лат. lemma — припущення), або
лематичним умовиводом. В залежності від
числа припущень (імплікацій) в більшому
засновку, леми поділяються на: дилеми − два
припущення, трилеми — три припущення,
полілеми — більше ніж три припущення.
34. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Правила умовно-розділового силогізмупоєднують правила умовно-категоричного та
розділово-категоричного силогізмів:
1. Ствердження імплікації відбувається від
підстави до наслідку, але не навпаки.
Заперечення імплікації відбувається від
наслідку до підстави, але не навпаки.
2. У розділовому судженні (при сильній
диз’юнкції) повинні бути перелічені усі
диз`юнкти.
35. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
ВИДИ ЛЕМ:дилема
—
умовнорозділовий
силогізм,
розділовий
засновок
якого
містить дві
альтернати
ви
трилема — умовно- полілема — умовнорозділовий силогізм, розділовий
розділовий засновок силогізм,
якого містить три розділовий
альтернативи
засновок якого
містить більше ніж
3 альтернативи
36. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Види дилем.За кількістю (причин і наслідків в імплікації)
дилеми поділяються на прості і складні.
За якістю (ствердження або заперечення)
дилеми поділяються на конструктивні та
деструктивні.
37. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Проста конструктивна дилема Проста деструктивна(а b)
дилема
(с b)
(а b)
а с
(а с)
b
b с
Формула:
а
((а b) (с b) (а с))→b – Формула:
закон логіки
((а b) (а с) ( b с))→ а –
закон логіки
38. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Складна конструктивна дилема Складна деструктивна дилема(а b)
(а b)
(с d)
(с d)
а с
b d
b d
а с
Формула:
Формула:
((а b) (с d) (а с))→(b d) – ((а b) (с d) ( b d))→( а с)
закон логіки
– закон логіки
39. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Приклади:Якщо людина є крадієм (a), то вона скоює злочин (b);
якщо людина є
вбивцею (c), то вона скоює злочин (b).
П. − крадій (a) або вбивця (c).
П. скоїв злочин (b).
Якщо правитель мудрий (a), то країна багатіє (b);
якщо правитель пройдисвіт (c) – країна бідніє (d).
Правитель буває мудрим (a) або пройдисвітом (c).
Країна може або багатіти (c), або бідніти (d).
40. 2. Умовиводи зі складними судженнями. Умовно -розділовий силогізм
Приклади:Якщо людина скоїла злочин (a), то вона порушила закон (b);
якщо людина скоїла злочин (a), то вона повинна нести
кримінальну відповідальність (c). П. не порушував закон ( b) та
не повинен нести кримінальної відповідальності ( c).
_____________________________________________
П. не скоював злочин ( a).
Якщо людина при пожежі стрибне з вікна (a), то вона може
отримати забиття (b); якщо ж людина спробує пройти сходами
(c), то вона може отримати опіки (d).
П. не отримав ані забиття ( b), ані опіків ( d).
П. не стрибав з вікна ( a) та не йшов сходами ( c).
41. 2. Умовиводи зі складними судженнями. Скорочені силогізми (ентимеми)
У міркуваннях ми використовуємо як повні силогізми, так ісилогізми, де пропущений (мається на увазі) один з засновків
або висновок. Такі силогізми називаються скороченими, або
ентимемами (із грец. «у думці»).
Види ентимем. У категоричному силогізмі виділяють три види
ентимем: із пропущеним більшим засновком, із пропущеним
меншим засновком і з пропущеним висновком.
Приклади:
1. «Харків» – це власне ім’я
Тому «Харків» пишеться з великої літери.
2. Всі власні імена пишуться з великої літери.
Тому «Харків» пишеться з великої літери.
3. Всі власні імена пишуться з великої літери.
«Харків» − це власне ім’я.
42. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
Послідовність силогізмів, з’єднаних улогічно пов’язане міркування, називається
полісилогізмом або складним силогізмом.
Структура полісилогізму. Елементарний
полісилогізм складається з двох силогізмів.
Силогізм, що надає підставу для засновку
наступного силогізму, називають
просилогізмом. Силогізм, у якому засновок
виявляється висновком попереднього
силогізму, називають епісилогізмом.
43. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
В залежності від порядку логічного зв’язку між судженнямирозрізняють два види полісилогізмів.
1. Прогресивний − якщо висновок попереднього силогізму стає
більшим засновком для наступного. В даному разі міркування
йде від більш загальних за обсягом понять до понять менших за
обсягом.
Схема:
a є b − просилогізм.
cєa
cєb
c є b − епісилогізм.
dєc
dєb
44. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
Наприклад:Кожен громадянин (a) повинен дотримуватись законів
своєї держави (b).
Всі юристи (c) – громадяни (a).
Всі юристи (c) повинні дотримуватись законів своєї
держави (b).
Всі судді (d) – юристи (c).
Всі судді (d) повинні дотримуватись законів своєї
держави (b).
45. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
2. Регресивний − якщо в ньому висновокпопереднього силогізму стає меншим засновком
наступного силогізму.
Схема:
a є b − просилогізм.
cєa
cєb
d є c − епісилогізм.
cєb
bєd
46. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
Приклад:Кожен громадянин (a) повинен дотримуватись законів
своєї держави (b).
Всі юристи (c) – громадяни (a).
Кожен юрист (с) повинен дотримуватись законів своєї
держави (b).
Адвокати (d) – це юристи (c).
Кожен юрист (с) повинен дотримуватись законів своєї
держави (b).
Дехто з тих, хто повинен дотримуватись законів своєї
держави (b), є адвокатами (d).
47. 2. Умовиводи зі складними судженнями. Полісилогізми. Сорит і епіхейрема
Полісилогізми можуть приймати скороченіформи.
Сорит – це полісилогізм, що складається зі
скорочених силогізмів (від грецьк. soritos —
купа). Він складається з декількох силогізмів і
має дві форми − прогресивний і регресивний
сорити.
Бувають складноскорочені силогізми, в яких
кожний засновок є висновком ентимеми.
Такий силогізм називається епіхейремою.
48. Приклади завдань з ЗНО
1. Проректор: Ми завжди маємо діяти, але лише в тому разі, якщо ми нерозгубилися. Тому нам зараз не варто зупинятися і чекати на вказівки.
Ректор: Той факт, що ми розгубилися, якраз і означає, що нам потрібно
зупинитися.
У наведеному діалозі слова ректора спрямовані на те, щоб:
А погодитись з істинністю умови міркувань проректора й не коментувати
його висновок.
Б заперечити висновок проректора, не обґрунтовуючи своєї позиції.
В заперечити неявну умову в міркуваннях проректора, що спростовує
обґрунтованість його висновку.
Г зробити висновок про хибність міркувань проректора, погоджуючись з
істинністю умови й заперечуючи висновок.
Д надати контрприклад до узагальнення, запропонованого
проректором.