Лекция Булевы алгебры Нормальные формы

1.

Алгебра Буля
И БУЛЕВЫ АЛГЕБРЫ

2.

Множество истинностных значений высказываний - {0,1}
Формула X определяет на множестве {0,1} унарную
операцию F F X (x), которая обозначается символом x и
называется отрицанием или дополнением переменной х.
Формулы X Y, X Y определяют на множестве {0,1}
бинарные операции F FX Y ( x, y) , F FX Y ( x, y ), которые обозначаются
соответственно символами x y, x y и называются дизъюнкцией и
конъюнкцией переменных х,y. Операция x y иногда называется
также объединением или суммой переменных х,y и обозначается
соответственно через x y или х+у. Операция x y иногда
называется также пересечением или произведением переменных
х,y и обозначается соответственно через x yили x y .
Алгебра B=({0,1}, , , ) впервые была введена в 19-ом веке
английским математиком Дж.Булем. Поэтому эта алгебра
называется алгеброй Буля.

3.

Теорема 1. Алгебра Буля B=({0,1}, , , ) удовлетворяет
свойствам:
1. a (b c) (a b) c,
a (b c) (a b) c
–
ассоциативность дизъюнкции и конъюнкции;
2. a b b a , a b b a– коммутативность дизъюнкции и
конъюнкции;
3. a a a , a a a – идемпотентность дизъюнкции и
конъюнкции;
a (b c) (a b) (a c)
4. a (b c) (a b) (a c) ,
–
дистрибутивность соответственно конъюнкции
относительно дизъюнкции и дизъюнкции
относительно конъюнкции;
5. (a ) a – идемпотентность дополнения;

4.

6.(a b) a b , (a b) a b – законы де Моргана;
7. a (a b) a ,a (a b) a – законы поглощения;
8. a a 1 , a a 0– характеристическое свойство
дополнения,
9. a 1 1 , a 1 a – характеристическое свойство
наибольшего элемента 1,
10. a 0 a , a 0 0 – характеристическое свойство
наименьшего элемента 0.

5.

Булевы алгебры
В общем случае алгебры типа ={ , , ,1,0}, где
, – символы бинарных операций конъюнкции
и дизъюнкции, – символ унарной операции
дополнения и 1,0 – символы 0-арных операций
фиксирования выделенных элементов 1,0,
удовлетворяющие перечисленным в теореме
свойствам, называются булевыми алгебрами.

6.

Примеры таких алгебр
n-ые декартовы степени Bn=({0,1}n; , , ) алгебры Буля B с
покомпонентно определенными для их элементов a (a1 ,..., an ) ,
b (b1 ,...,bn ) операциями дизъюнкции a b (a1 b1 ,..., an bn ) ,
конъюнкции a b (a1 b1 ,..., an bn ) и отрицания a (a1 ,..., an )
Алгебра P(X)=(P(X), , , ,X, ) всех подмножеств непустого
множества X с теоретико-множественными операциями
объединения , пересечения , дополнения и фиксирования
выделенных элементов X, .

7.

Булевы многочлены и
булевы функции
ЛЕКЦИЯ 8

8.

Булевы многочлены
Для описания алгебраических свойств булевых
алгебр используются формулы, которые
называются булевыми многочленами и которые
образованы из булевых переменных
x,y,…(принимающих значения 0,1) и символов
булевых операций +, , по следующим правилам:
все булевы переменные x,y,… и символы 0,1 – булевы
многочлены;
если p и q – булевы многочлены, то таковыми являются
выражения p q , p q , p .

9.

При этом скобки в многочленах используются для
указания порядка выполнения операций над
переменными и по возможности опускаются с учетом
следующего приоритета выполнения булевых
операций: , ,+.
Пример. Булев многочлен x y x можно
записать в виде x y x .
Если булев многочлен p образован с помощью
переменных x1 ,..., xn , то он называется булевым
многочленом от n переменных и обозначается
символом p( x1 ,..., xn ) .
Множество всех булевых многочленов от n
переменных обозначим через Pn

10.

Булева функция
Если в булев многочлен p( x1 ,..., xn ) вместо
переменных x1 ,..., xn подставить произвольные
значения a1 ,..., an из множества B и для полученного
выражения p(a1,..., an ) произвести все вычисления в
булевой алгебре B по правилу построения исходного
булева многочлена, то в результате получится
некоторый элемент p(a1,..., an ) алгебры B.
Значит, каждый булев многочлен p( x1,..., xn ) определяет
отображение p : Bn B , которое каждому
упорядоченному набору (a1 ,..., an ) Bn n элементов
множества {0,1} ставит в соответствие элемент p(a1,...,an )
этого же множества {0,1}. Такое отображение p
называется булевой (полиномиальной) функцией,
определяемой булевым многочленом p.

11.

Пример
Булев многочлен p x y x определяет булеву
полиномиальную функцию p со значениями:
p 0,0 0 0 0 1 0 1,
p 0,1 0 1 0 0 0 0,
p 1,0 1 0 1 0 1 1,
p 1,1 1 1 1 0 1 1.

12.

Эквивалентные булевы многочлены
Булевы многочлены p, q Pn называются
эквивалентными, если они определяют одну и ту же
булеву полиномиальную функцию, т.е. выполняется
равенство p q.
Это записывается формулой p ~ q или просто p q.
Замечание. Бинарное отношение ~ является
эквивалентностью на множестве Pn , которое разбивает это
множество на классы эквивалентности p {q Pn : p ~ q} ,
порождаемые элементами p Pn и образующие фактормножество Pn / ~ { p : p Pn }.
Полные системы представителей фактор-множества Pn / ~
называются системами нормальных форм булевых
многочленов.

13.

СДНФ и СКНФ
Для булевой переменной x и значения {0,1} введем обозначение:
x, если 1,
x
x , если 0,
которое называется литерой. Литера или конъюнкция
(соответственно, дизъюнкция) литер называется конъюнктом
(соответственно, дизъюнктом).
Конъюнкт (дизъюнкт) называется совершенным, если он содержит
все булевы переменные рассматриваемой формулы.
Дизъюнт или конъюнкция (совершенных) дизъюнктов называется
(совершенной) конъюнктивной нормальной формой. Для названия
таких форм используются сокращения КНФ и СКНФ,
соответственно.
Конъюнкт или дизъюнкция (совершенных) конъюнктов называется
(совершенной) дизъюнктивной нормальной формой.
Для названия таких форм используются сокращения ДНФ и СДНФ,
соответственно.

14.

Теорема 2
Любая булева функция f:Bn B является булевой
функцией следующих булевых многочленов:
pf
qf
1
n
f
,...,
x
...
x
1 n 1 n
1 ,..., n B n
1
n
(
f
,...,
x
...
x
1
n
n )
1
1 ,..., n B n

15.

Следствие 3
Если булева функция f:Bn B не равна тождественно нулю, то она является
булевой полиномиальной функцией следующей совершенной дизъюнктивной
нормальной формы
pf
x1 ...x n
1
n
1 ,..., n B n ,
f 1 ,..., n 1
которая называется совершенной дизъюнктивной нормальной формой
(сокращенно СДНФ) функции f .
Если булева функция f:Bn B не равна тождественно единице, то она является
булевой полиномиальной функцией следующей совершенной конъюнктивной
нормальной формы
1
n
qf
(
x
...
x
n )
1
1 ,..., n B n ,
f 1 ,..., n 0
которая называется совершенной конъюнктивной нормальной формой
(сокращенно СКНФ) функции f .
В силу свойств булевых операций СДНФ (соответственно, СКНФ) функции f
определяется однозначно с точностью до порядка составляющих эту форму
конъюнктов (соответственно, дизъюнктов) и порядка литер в этих конъюнктах
(соответственно, дизъюнктах).

16.

Алгоритм нахождения СДНФ и СКНФ
функции f:Bn B:
1.
2.
3.
Составить таблицу значений функции f и добавить к
ней два дополнительных столбца с заголовками
«Совершенные конъюнкты» и «Совершенные
дизъюнкты».
Если при значениях x1 k1,..., xn kn значение функции f
равно 1, то в соответствующей строке таблицы в
столбце «Совершенные конъюнкты» записать
конъюнкт x1k1 ...xnk n и в столбце «Совершенные
дизъюнкты» сделать прочерк (при этом x1 x и x 0 x ).
Если при значениях x1 m1,..., xn mn значение функции f
равно 0, то в соответствующей строке таблицы в
столбце «Совершенные дизъюнкты» записать
дизъюнкт x1m1 ... xnmn и в столбце «Совершенные
конъюнкты» сделать прочерк.

17.

Совершенные
конъюнкты
…
Совершенные
дизъюнкты
…
1
x1k1 ...xnk n
–
...
…
…
…
mn
...
0
–
x1m1 ... xnmn
…
...
…
…
…
x1
…
xn
...
f x1 ,..., xn
…
…
…
...
…
k1
…
kn
...
…
…
…
m1
…
…
…
k
k
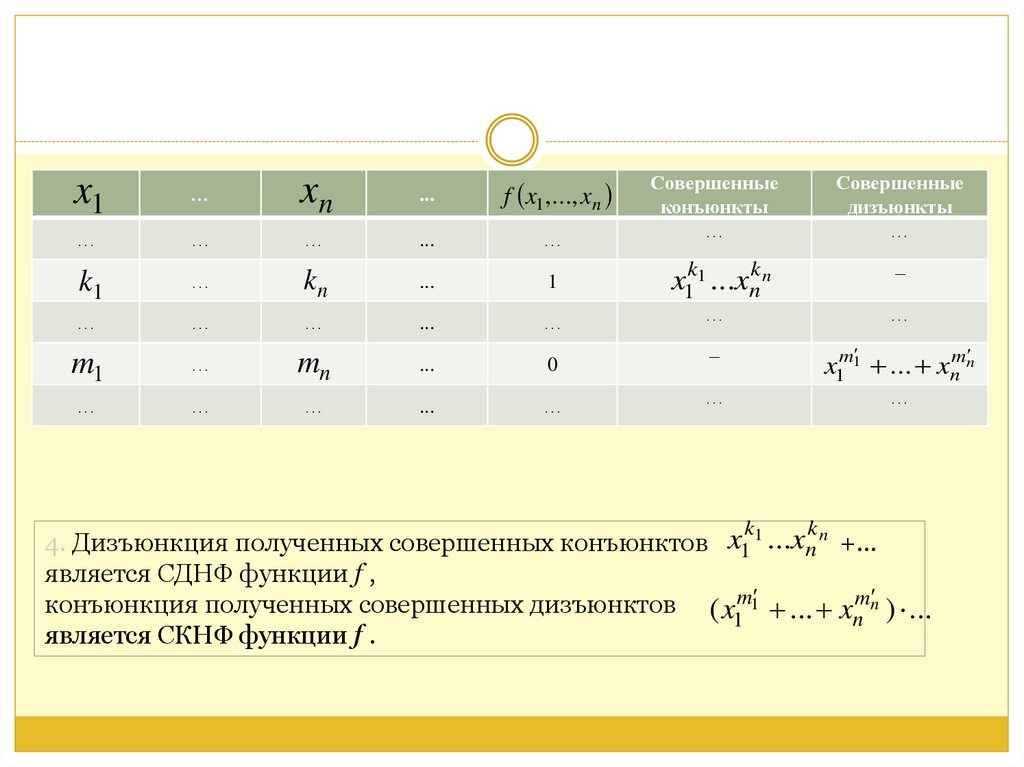
4. Дизъюнкция полученных совершенных конъюнктов x1 1 ...xn n +…
является СДНФ функции f ,
конъюнкция полученных совершенных дизъюнктов ( x m1 ... xnmn ) ...
1
является СКНФ функции f .