Beamer__Module_2__Lesson_11_1

1.

Планиметрия
Модуль 2. Занятие 11.1
Wild Mathing
25 июня 2024 г.
Wild Mathing
Планиметрия

2.

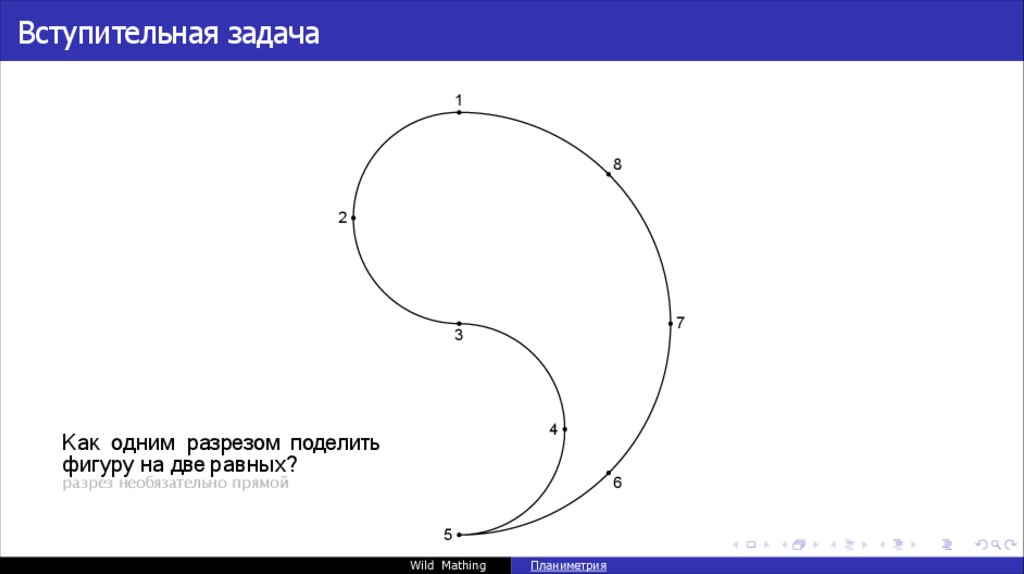
Вступительная задача
Как одним разрезом поделить
фигуру на две равных?
разрез необязательно прямой
Wild Mathing
Планиметрия

3.

Вступительная задача
1
8
2
7
3
4
Как одним разрезом поделить
фигуру на две равных?
разрез необязательно прямой
6
5
Wild Mathing
Планиметрия

4.

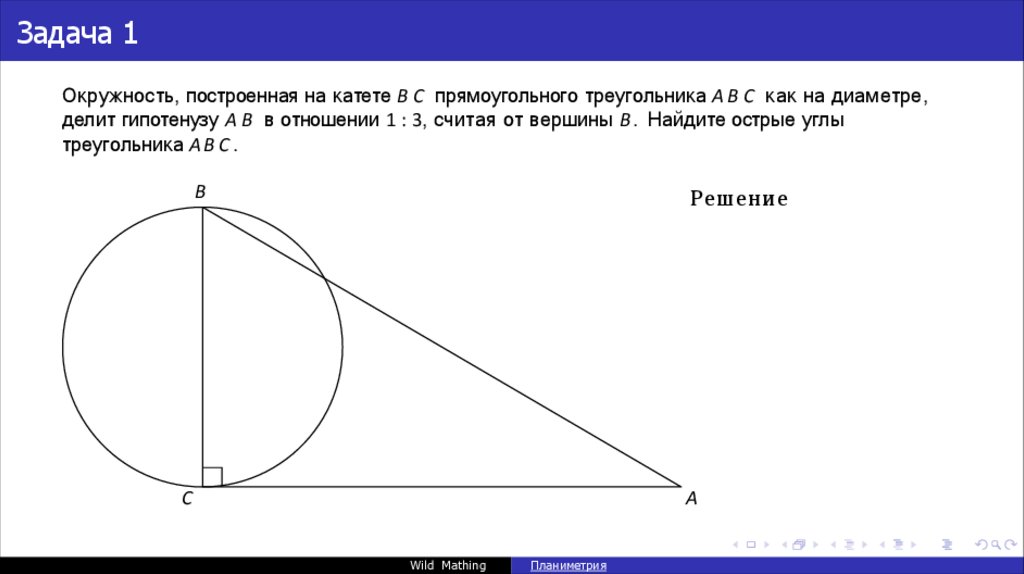
Задача 1
Окружность, построенная на катете B C прямоугольного треугольника A B C как на диаметре,
делит гипотенузу A B в отношении 1 : 3, считая от вершины B . Найдите острые углы
треугольника A B C .
B
Решение
C
A
Wild Mathing
Планиметрия

5.

Полезный факт
Свойство высоты тр-ка, проведенной из вершины прямого угла
Высота прямоугольного треугольника, проведенная из вершины прямого угла, равна
среднему геометрическому отрезков, на которые делит гипотенузу.
B
Доказательство
β
Пусть C H — высота треугольника A B C с прямым
углом при вершине C , ∠ B A C = α, ∠ A B C = β.
H
α
C
A
Wild Mathing
Планиметрия

6.

Задача 2
Найдите площадь треугольника, если две его стороны равны 27 и 29, а медиана, проведённая к
третьей, равна 26.
B
Решение
Пусть A M = 26 — медиана треугольника A B C , в
котором A B = 27, A C = 29.
M
A
C
Wild Mathing
Планиметрия

7.

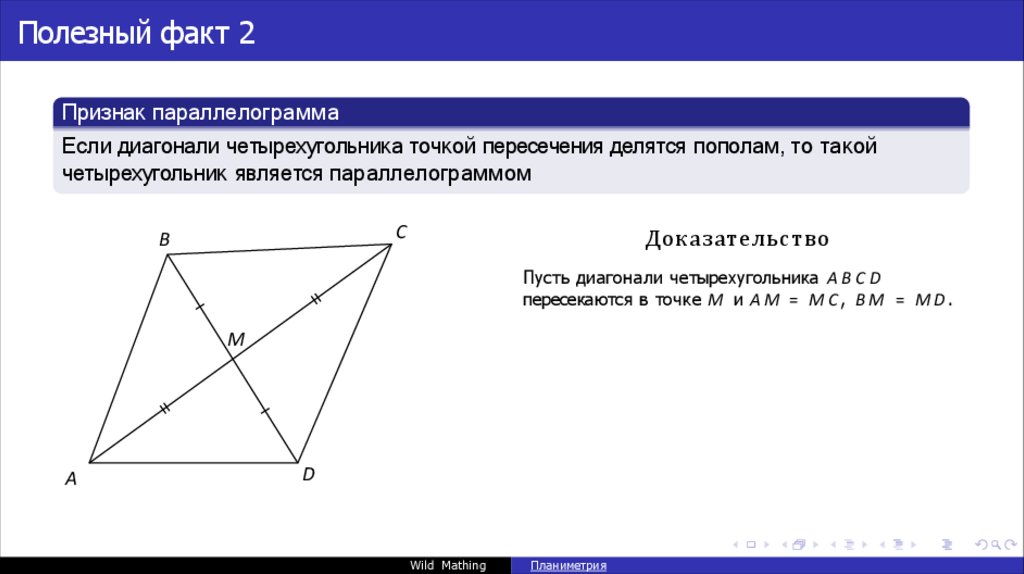
Полезный факт 2
Признак параллелограмма
Если диагонали четырехугольника точкой пересечения делятся пополам, то такой
четырехугольник является параллелограммом
C
B
Доказательство
Пусть диагонали четырехугольника A B C D
пересекаются в точке M и A M = M C , B M = M D .
M
A
D
Wild Mathing
Планиметрия

8.

Задача 3
В треугольнике A B C известны стороны B C = a, A C = b, A B = c. Найдите длину медианы m a ,
проведенную из вершины A.
B
Решение
Пусть точка A ′
симметрична точке A от-но M .
Тогда четырехугольник A B A ′ C — параллелограмм
по соответствующему признаку.
M
A
C
Wild Mathing
Планиметрия

9.

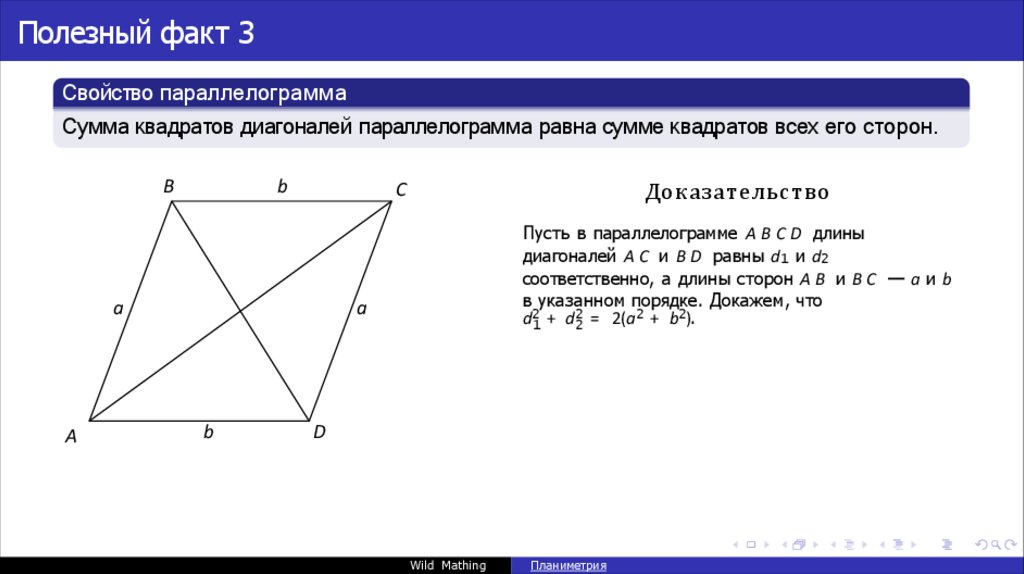
Полезный факт 3
Свойство параллелограмма
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
B
b
a
A
Доказательство
C
Пусть в параллелограмме A B C D длины
диагоналей A C и B D равны d1 и d2
соответственно, а длины сторон A B и B C — a и b
в указанном порядке. Докажем, что
d21 + d22 = 2(a2 + b2).
a
b
D
Wild Mathing
Планиметрия

10.

Задача 4
В равнобедренной трапеции основания равны 40 и 24, а её диагонали взаимно перпендикулярны.
Найдите площадь трапеции.
B
C
Решение
Пусть в трапеции A B C D с основаниями A D = 40
и B C = 24 диагонали взаимно перпендикулярны.
A
D
Wild Mathing
Планиметрия

11.

Полезный факт 4
Свойство медианы тр-ка, проведенной из вершины прямого угла
Если медиана прямоугольного треугольника проведена из вершины прямого угла, то она
равна половине гипотенузы.
A
Доказательство
Пусть C M — медиана прямоугольного
треугольника A B C , проведенная из вершины
прямого угла C .
M
C
B
Wild Mathing
Планиметрия

12.

Задача 5
Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
B
C
Решение
Пусть в трапеции A B C D основания B C и A D
равны 14 и 40 соответственно, а радиус описанной
около нее окружности с центром O равен 25.
O
A
D
Wild Mathing
Планиметрия

13.

Задача 5. Случай 2
Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
B
C
Решение
Пусть в трапеции A B C D основания B C и A D
равны 14 и 40 соответственно, а радиус описанной
около нее окружности с центром O равен 25.
A
D
O
Wild Mathing
Планиметрия

14.

Полезный факт 5
Свойство равных хорд окружности
Равные хорды окружности стягивают равные дуги.
B
C
Доказательство
Пусть A B и C D — равные хорды
окружности с центром O.
O
A
D
Wild Mathing
Планиметрия

15.

Спасибо за занятие!
Смело пишите вопросы в комментариях
Wild Mathing
Wild Mathing
Спасибо за занятие!

16.

Ответы на вопросы
Wild Mathing
Спасибо за занятие!