Решение геометрических задач при подготовке к ЕГЭ

1. Решение геометрических задач при подготовке к ЕГЭ

2. Содержание

1. Справочная информация.
2. Задания диагностических работ по типу ЕГЭ:
- 1;
- 1 для самостоятельного решения
- 2;
- 2 для самостоятельного решения
- 3;
- 3 для самостоятельного решения
- 2 часть;
- 2 часть для самостоятельного решения

3. СПРАВОЧНАЯ ИНФОРМАЦИЯ

4. СПРАВОЧНАЯ ИНФОРМАЦИЯ

треугольники
четырехугольники
правильные
многоугольники
окружность
векторы

5.

Справочные сведения
Треугольники
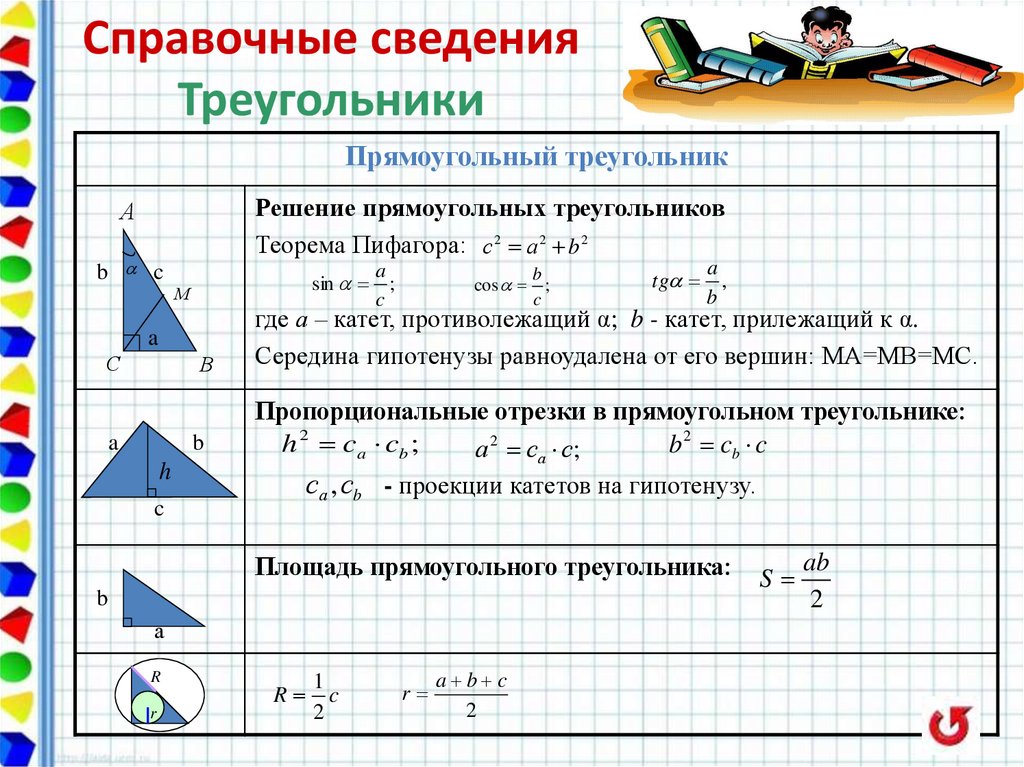
Прямоугольный треугольник
Решение прямоугольных треугольников
Теорема Пифагора: с 2 а 2 b 2
А
b c
sin
М
a
С
В
a
b
h
c
a
;
c
b
cos ;
c
tg
a
,
b
где а – катет, противолежащий α; b - катет, прилежащий к α.
Середина гипотенузы равноудалена от его вершин: МА=МВ=МС.
Пропорциональные отрезки в прямоугольном треугольнике:
h 2 ca cb ;
b 2 cb c
а 2 са с;
са , сb - проекции катетов на гипотенузу.
Площадь прямоугольного треугольника:
b
а
R
r
R
1
c
2
r
a b c
2
S
ab
2

6.

Справочные сведения
Треугольники
Равнобедренный треугольник
h
Медиана, биссектриса и высота,
проведённые к основанию, совпадают.
Высоты, проведённые к боковым сторонам,
равны;
медианы, проведённые к боковым сторонам,
равны;
биссектрисы углов при основании равны.

7. Справочные сведения Треугольники

Произвольный треугольник
Площадь треугольника:
с
b
S
h
1
a b sin ;
2
S
S = p ∙ r;
abc
;
4R
S p ( p a) ( p b) ( p c) ,
S
1
a h
2
где р – полупериметр
a
0
Сумма углов в треугольнике: А В С 180
a
b
c
Теорема синусов:
А
b
c
C
sin A
a
B
R
r
sin B
sin C
2
2
2
Теорема косинусов: с a b 2ab sin
R
abc
4S
r
2S
p

8.

Справочные сведения
Треугольники
А
С
В
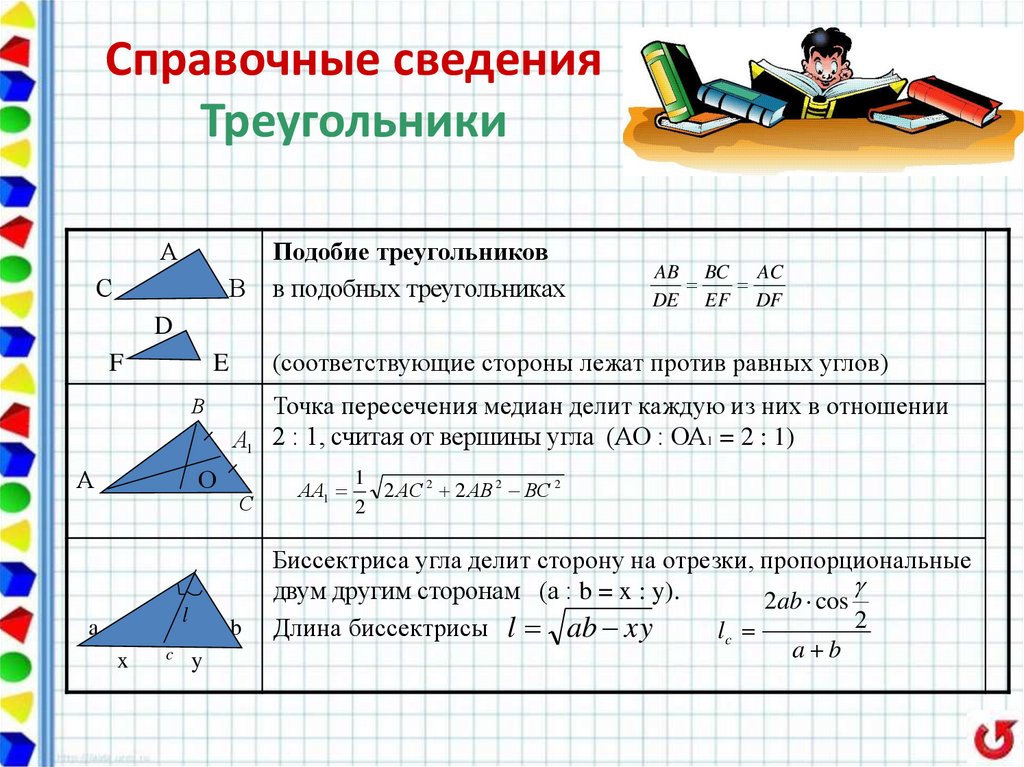
Подобие треугольников
в подобных треугольниках
AB BC AC
DE EF DF
D
F
В
А
О
l
a
x
(соответствующие стороны лежат против равных углов)
E
c
Точка пересечения медиан делит каждую из них в отношении
А1 2 : 1, считая от вершины угла (АО : ОА1 = 2 : 1)
С
b
y
АА1
1
2 АС 2 2 АВ 2 ВС 2
2
Биссектриса угла делит сторону на отрезки, пропорциональные
двум другим сторонам (а : b = x : y).
2ab cos
2
Длина биссектрисы l ab xy
lc
a b

9.

Справочные сведения
Четырехугольники
Параллелограмм
Свойства
ABCD – параллелограмм
С AB CD, BC AD, AB = CD, BC = AD,
В
A C , B D
О
A B B C C D A D 1800 ,
φ
α
A
AO = OC, BO = OD,
D
2 ( AB 2 BC 2 ) AC 2 BD 2 .
Признаки
AB CD, BC AD ABCD – параллелограмм;
AO = OC, BO = OD ABCD – параллелограмм;
AB = CD, BC = AD ABCD – параллелограмм;
AB = CD, AB CD ABCD – параллелограмм;
BC = AD, BC AD ABCD – параллелограмм
Площадь:
1
S aha ;
2
S ab sin ;
S
1
d 1 d 2 sin
2

10.

Справочные сведения
Четырехугольники
Прямоугольник
В
С
О
A
D
Свойства
ABCD – прямоугольник
AB CD, BC AD, AB = CD, BC = AD;
А С В D 900 ;
AO = BO = CO = DO
(О – центр описанной окружности, ОА = R).
Признаки
ABCD – параллелограмм, АС = BD ABCD – прямоугольник.
ABCD – параллелограмм, А 90 0 ABCD – прямоугольник.
Площадь
S ab
S
1 2
d sin
2

11.

Справочные сведения
Четырехугольники
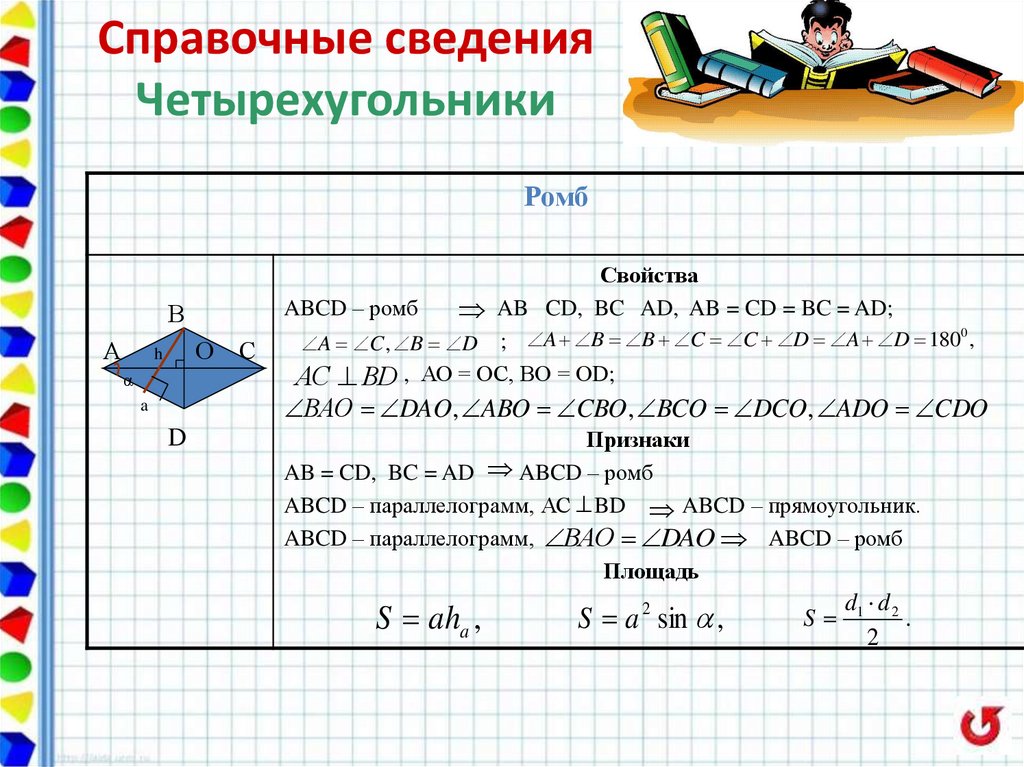
Ромб
В
А
О
h
α
С
Свойства
ABCD – ромб
AB CD, BC AD, AB = CD = BC = AD;
0
A C , B D ; A B B C C D A D 180 ,
АС ВD , АО = ОС, ВО = ОD;
ВАО DAO, ABO CBO , BCO DCO, ADO CDO
a
D
Признаки
AB = CD, BC = AD ABCD – ромб
ABCD – параллелограмм, АС BD ABCD – прямоугольник.
ABCD – параллелограмм, ВАО DAO ABCD – ромб
Площадь
S aha ,
S a 2 sin ,
S
d1 d 2
.
2

12.

Справочные сведения
Четырехугольники
Квадрат
Свойства
С ABCD – квадрат AB CD, BC AD, AB = CD = BC = AD;
А С В D 900 ; АС ВD , AO = BO = CO = DO;
В
а
О
ВАО АВО СВО ВСО DCO CDO ADO DAO 450
d
A
D
Признаки
ABCD – прямоугольник, AB = CD = BC = AD ABCD – квадрат;
0
ABCD – ромб, А 90 ABCD – квадрат.
Площадь
2
S a
2
d
S
2

13.

Справочные сведения
Четырехугольники
Произвольная трапеция
B
C
O
φ
A
D
Треугольники AOD и СОВ подобны.
Треугольники АОВ и DOC равновелики (их площади равны)
1
S d1d 2 sin
Площадь трапеции:
2
a
m
h
Площадь трапеции:
b
c
Средняя линия трапеции:
S
m
a b
2
a b
h m h
2
Вписанная в окружность трапеция – равнобедренная.
В описанной около окружности трапеции:
высота равна диаметру: h = 2 r;
b
сумма оснований равна сумме боковых сторон: a + b = c + d;
r
d
полусумма боковых сторон равна средней линии: c + d = m;
a
(боковая сторона равнобедренной трапеции равна средней линии).

14.

Справочные сведения
Четырехугольники
Равнобедренная трапеция
В
С
A
Углы при оснований равны: А D, B C
D
B
C
O
A
D
B
C
h
m
A
H
Диагонали равны: АС = ВD;
отрезки диагоналей равны: АО = DO, BO = CO;
углы, образованные основанием и диагоналями, равны:
CAD ADB , DBC ACB
Основание высоты, проведённой к большему основанию, делит основание
на отрезки, равные a b и a b
(если ВН – высота, то DH = m, где m –
2
2
средняя линия).
D
Если в равнобедренной трапеции диагонали перпендикулярны, то высота,
проведённая к основанию, равна средней линии: h = m. В этом случае
площадь трапеции можно найти по формуле: S h 2 m 2

15.

Справочные сведения
Правильные многоугольники
Сумма углов многоугольника
В выпуклом многоугольнике сумма углов равна 1800 (т 2),
где n – число сторон (вершин) многоугольника.
Свойства правильного многоугольника
Все стороны равны, все углы равны,
О – центр вписанной и описанной окружностей,
R – радиус описанной окружности, лежит на биссектрисе угла,
r – радиус вписанной окружности, лежит на серединном
перпендикуляре к стороне.
О
R
r
A
B
1 3600 : n,
1
2
3
Центральный угол:
0
Внутренний угол: 2 180 (n 2) ,
n
Внешний угол равен центральному углу: 3 360 0 : n.
a2 3
S3
4

16.

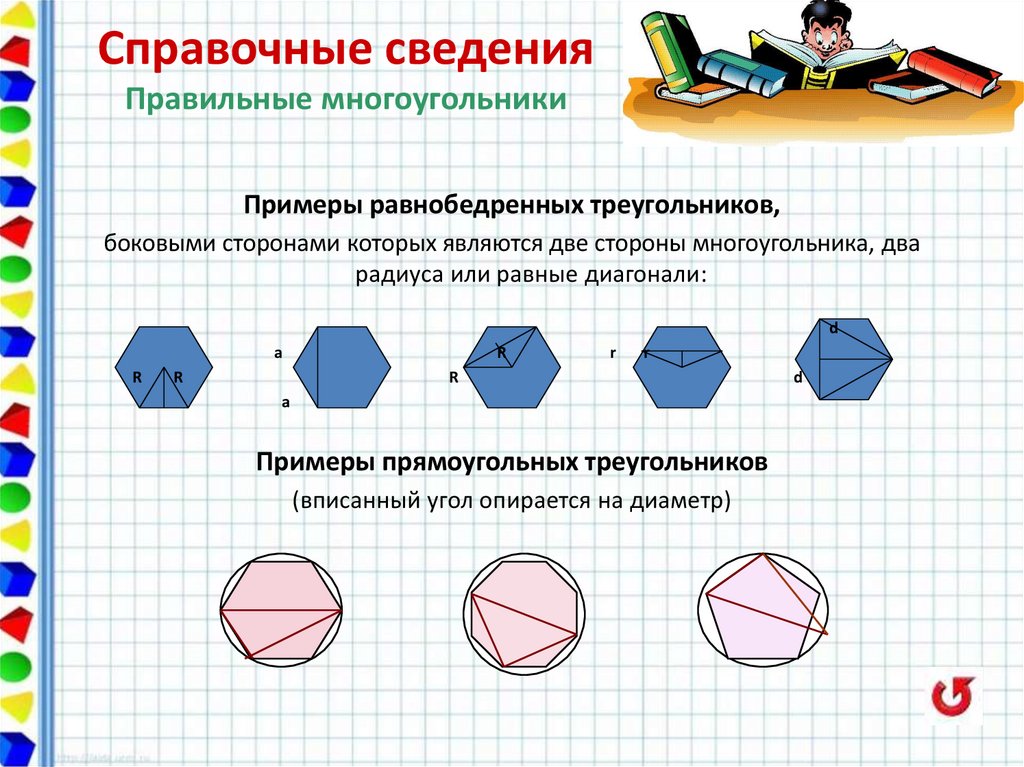
Справочные сведения
Правильные многоугольники
Примеры равнобедренных треугольников,
боковыми сторонами которых являются две стороны многоугольника, два
радиуса или равные диагонали:
d
a
R
R
R
r
r
R
a
Примеры прямоугольных треугольников
(вписанный угол опирается на диаметр)
d

17.

Справочные сведения
Окружность
Окружность и её элементы
.
Радиус, проходящий через середину хорды, перпендикулярен
этой хорде.
Радиус, перпендикулярный хорде, делит её пополам.
.
Радиус, проведённый в точку касания, перпендикулярен
касательной.
.
Отрезки касательных, проведённых из одной точки, равны.
Центр окружности лежит на биссектрисе угла, образованного
касательными, проведёнными из одной точки.
.
.
Вписанный угол, опирающийся на диаметр, равен
90
0

18.

Справочные сведения
Окружность
Окружность и её элементы
Градусная мера центрального угла равна градусной мере дуги,
на которую он опирается.
m
m
n
Вписанный угол измеряется половиной дуги, на которую он
опирается.
n
Вписанные углы, опирающиеся на одну дугу, равны.
Если две хорды окружности пересекаются, то произведение
отрезков одной хорды равно произведению отрезков другой
хорды.

19.

Справочные сведения
Окружность
Окружность, вписанная в треугольник
Отрезок, соединяющий центр окружности и точку её
касания со стороной, перпендикулярен этой стороне.
Отрезки двух соседних сторон от общей вершины до
точек касания равны между собой.
Центр вписанной окружности лежит на биссектрисе
угла, образованного двумя сторонами.

20.

Справочные сведения
Окружность
Окружность, описанная около треугольника
Центр описанной окружности лежит на серединном
перпендикуляре к любой из сторон треугольника.
Если прямоугольный треугольник вписан в
окружность, то его гипотенуза является диаметром
окружности.
Угол вписанного в окружность треугольника в 2 раза
меньше центрального угла, опирающегося на ту же
дугу, и равен любому другому вписанному углу,
опирающемуся на ту же дугу.

21.

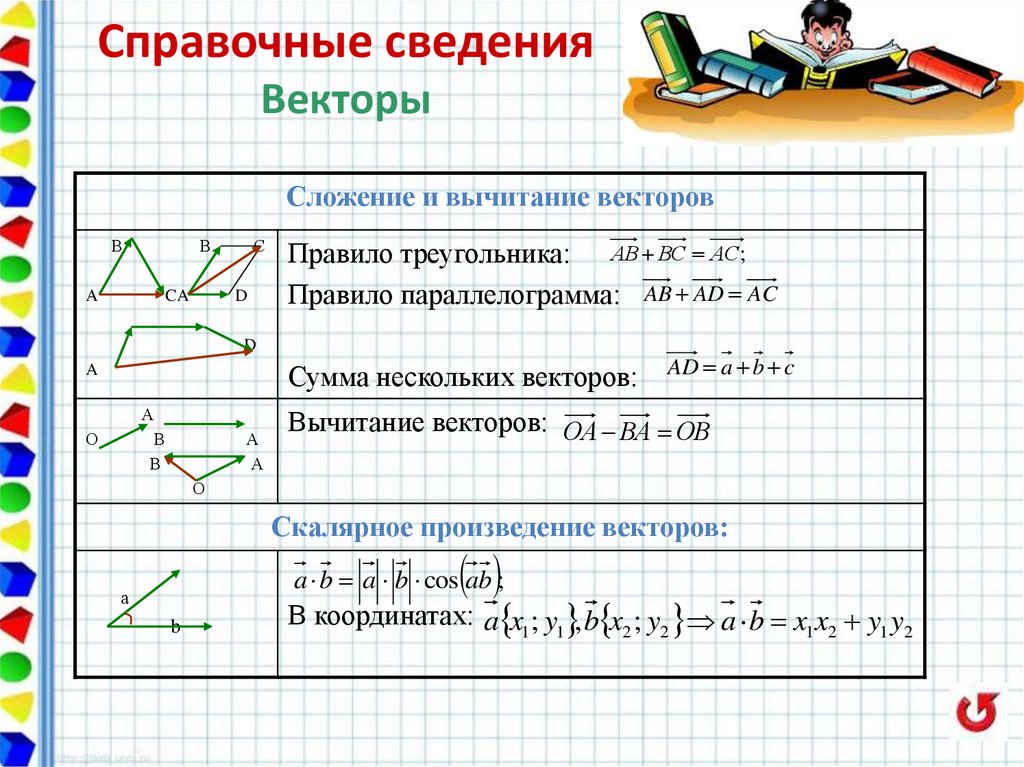
Справочные сведения
Векторы
Сложение и вычитание векторов
В
В
A
CA
С
D
Правило треугольника: АВ ВС АС;
Правило параллелограмма: AB AD AC
D
Сумма нескольких векторов:
A
А
В
В
О
А
А
AD a b c
Вычитание векторов: ОА ВА ОВ
О
Скалярное произведение векторов:
a b a b cos ab ;
а
b
В координатах: a x1; y1 , b x2 ; y2 a b x1 x2 y1 y2

22. Треугольники

Диагностическая работа ЕГЭ
1. В треугольнике АВС С 90, 0
АВ= 30, АС 3 19 . Найдите sin А.
А
2. В треугольнике АВС С 90
,0
20
АВ =29,cos B
. Найдите АС.
А
ВС АВ 2 АС 2 30 2 (3 19 ) 2 27
30
3 19
С
В sin A
20
29
BC 20
BC BC
cos B
AB 29
cos B
29
29
cos B
20
29
С
АС 29 2 20 2 9 49 21.
В
С
3. В треугольнике АВС АС=ВС,
3
tgA
АВ = 8,
. Найдите высоту СН.
4
3
4
CH 3
CH
CH
CH
tgA
AH 0,5 AB
4
tgA
tgA
В
4. В равнобедренном треугольнике АВС
с основанием АС боковая сторона АВ =
10, а высота, проведённая к основанию,
равна 2 21 . Найдите косинус угла А.
8 Н
3
4
В
10
А
АН АВ 2 ВН 2 10 2 (2 21) 2 4
cos A
2 21
?
А
BC 27
0,9
AB 30
Н
С
АH 4
0,4
AB 10

23. Треугольники Диагностическая работа ЕГЭ задания для самостоятельного решения

5. В равнобедренном треугольнике АВС с основанием АС боковая
8
сторона АВ = 17, cos A
. Найдите высоту, проведённую к
17
основанию.
15
6. В треугольнике АВС С 90 , АВ= 14, АС = 7 3 .
Найдите sin А.
0,5
7. В равнобедренном треугольнике АВС с основанием АС боковая
сторона АВ = 10, а высота, проведённая к основанию, равна 19 .
Найдите косинус угла А.
0,9
0
8. В треугольнике АВС
Найдите АВ.
С 900 , sin A
8
, AC 2 17 .
9
18

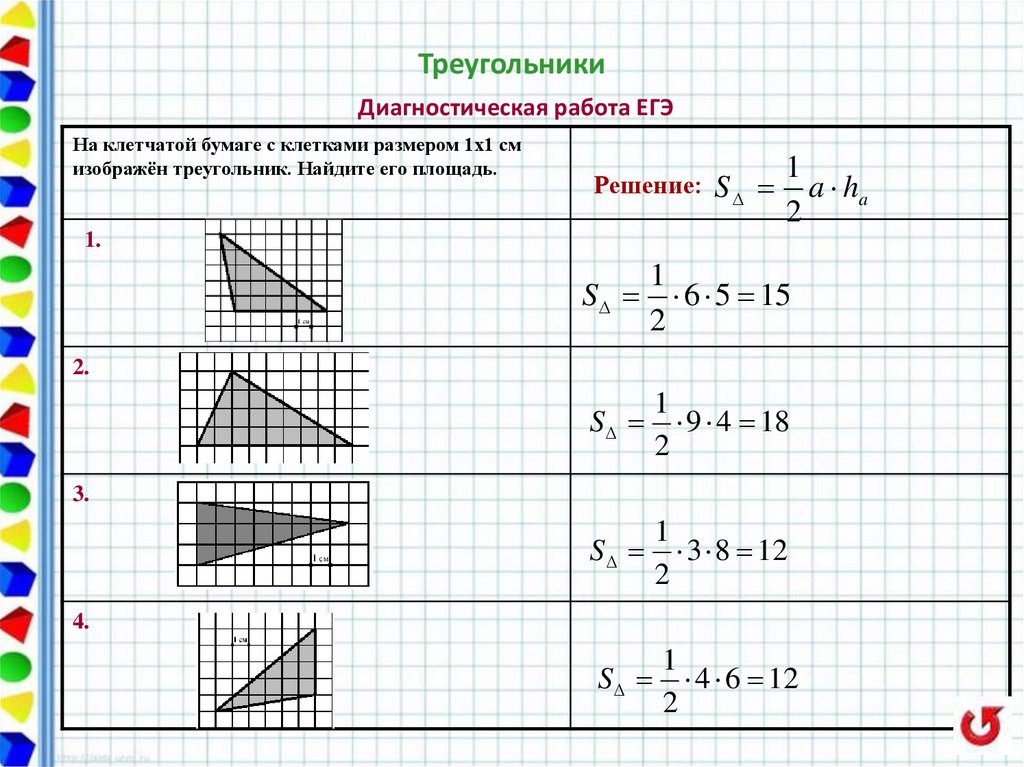
24. Треугольники Диагностическая работа ЕГЭ

На клетчатой бумаге с клетками размером 1х1 см
изображён треугольник. Найдите его площадь.
Решение: S
1
a ha
2
1.
S
1
6 5 15
2
S
1
9 4 18
2
S
1
3 8 12
2
S
1
4 6 12
2
2.
3.
4.

25. Треу0гольники Диагностическая работа ЕГЭ

На клетчатой бумаге с клетками размером
1х1 см изображён треугольник. Найдите его
площадь.
5.
Решение
S S1 S2
S2
1
6 6 18
2
1
S 2 2 ( 5 1) 1 6
2
S1
S1
S 18 6 12
S S1 S2
6.
1
6 4 12
2
1
S2 6 2 6
2
S1
S1
S2
S 12 6 6
7.
S2
S1
S S1 S2
S1
1
6 6 18
2
1
S 2 2 ( 5 1) 1 6
2
S 18 6 12

26. Треугольники Диагностическая работа ЕГЭ

Найдите площадь треугольника, изображённого на
рисунке.
8.
1
a ha
2
У
5
2
1
4 3 6
2
S
1
5 3 7,5
2
S
1
6 3 9
2
6
У
2
0
S
Х
0
10.
S
5
2
9.
Решение:
Х
1
6
У
4
1
0
1
3
9
Х

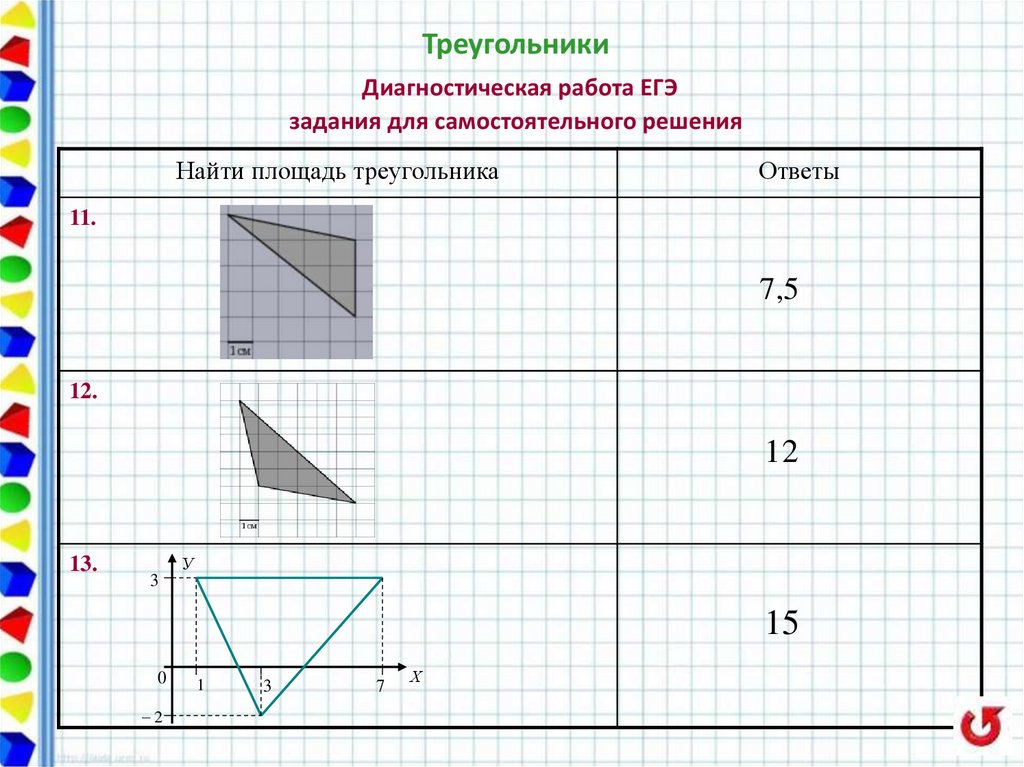
27. Треугольники Диагностическая работа ЕГЭ задания для самостоятельного решения

Найти площадь треугольника
Ответы
11.
7,5
12.
12
13.
У
3
15
0
2
1
3
7
Х

28. Треугольники

1. Площадь параллелограмма АВСD равна 16, диагональ АС равна 2, ACD 45 0.
Найдите сторону ВС.
Решение:
1. SACD = 0,5∙SABCD = 0,5∙16 = 8
1
2
2
2
СD
8
CD
8
:
8 2.
В
С
0
2
2
2
SACD = 0,5∙AC∙CD∙sin 45
45
2
0
8 2
А
D
2. По свойству параллелограмма: ВC = AD
AD 2 AC 2 DC 2 2 AC DC cos C
По теореме косинусов:
AD 2 2 2 (8 2 ) 2 2 2 8 2 cos 45 0
AD 2 4 128 32
AD 2 100
AD 10
AD 10
-10 не удовлетворяет смыслу задачи.
Ответ: 10.

29. Треугольники Задачи 11 для самостоятельного решения

1. Точка О является центром окружности, описанной около треугольника
АВС. Найдите площадь треугольника АОС, если известно, что ВС = 6,
АСВ 150 , САВ 300.
(Ответ: 18)
2. В равнобедренный прямоугольный треугольник с катетом, равным 1,
вписан квадрат, имеющий с треугольником общий прямой угол.
Найдите периметр квадрата.
(Ответ: 2)
3. В равнобедренном треугольнике синус угла при основании равен 0,8, а
радиус вписанной окружности равен 6. Найдите периметр данного
треугольника.
(Ответ: 64)
4. В равнобедренном треугольнике АВС, с основанием АС медиана ВМ и
высота СН пересекаются в точке К. Найдите площадь треугольника АВС,
если известно, что СК = 1, а косинус угла при вершине В равен 0,8.
(Ответ:2,7)

30. Диагностическая работа ЕГЭ

С -2.1 В прямоугольном параллелепипеде ABCDA1В1C1D1, у которого AB = 6,
BC = 6, CC1 = 4, найдите тангенс угла между плоскостями АCD1 и А1В1С1.
D1
С1
А1
В1
Решение:
1) Вместо плоскости А1В1С1 возьмём параллельную ей
плоскость АВС.
4
D
С
Е
А
6
В
6
2) Пусть Е – середина АС.
D1 E AC, DE AC DED1
3) Из прямоугольного треугольника D1DE находим:
Ответ: 2 2
.
3
- линейный угол искомого угла.
tg DED1
DD1
4
2 2
.
DE 3 2
3

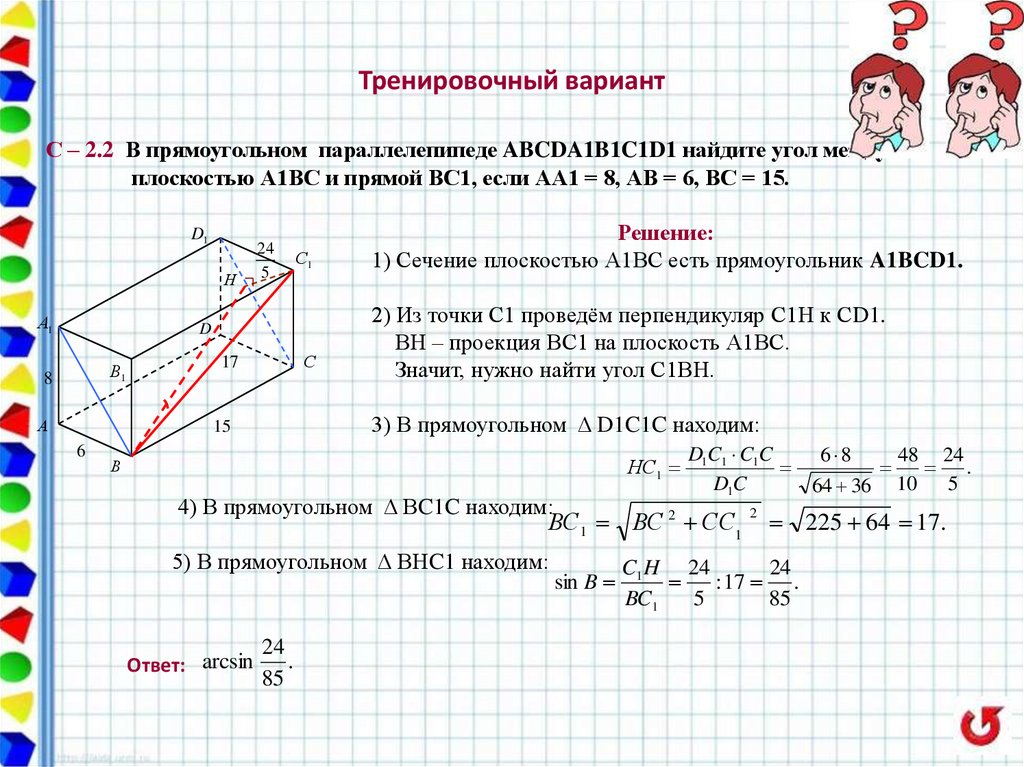
31. Тренировочный вариант

С – 2.2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между
плоскостью А1ВС и прямой ВС1, если АА1 = 8, АВ = 6, ВС = 15.
D1
Н
А1
24
5
С1
D
В1
8
А
С
17
2) Из точки С1 проведём перпендикуляр С1Н к СD1.
ВН – проекция ВС1 на плоскость А1ВС.
Значит, нужно найти угол С1ВН.
3) В прямоугольном Δ D1C1C находим:
15
6
Решение:
1) Сечение плоскостью А1ВС есть прямоугольник A1BCD1.
НС1
В
4) В прямоугольном Δ ВC1C находим:
D1C1 C1C
6 8
48 24
.
D1C
64 36 10 5
ВС 1 ВС 2 СС1
5) В прямоугольном Δ ВНC1 находим:
Ответ: arcsin
24
.
85
sin B
2
225 64 17.
C1 H 24
24
: 17 .
BC1
5
85

32. Диагностическая работа ЕГЭ

С – 2.3 В кубе ABCDA1B1C1D1 все рёбра равны 1. Найдите расстояние
от точки С до прямой АD1.
С1
D1
А1
А
Решение:
1) Построим отрезки СD1 и АС.
2
H
2
2) Искомое расстояние равно длине
D
С
2
перпендикуляра СН, проведённого к прямой АD1.
В
Этот перпендикуляр является медианой
равностороннего треугольника АСD1 со стороной
В1
АС АВ 2 ВС 2 1 1 2.
3)
2
2
1
3
6
2
2
2
СН АС АН 2
0,5 6.
2
2
2
2
Ответ:
0,5 6.

33. Треугольники Диагностическая работа ЕГЭ задания для самостоятельного решения

2.4 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между
плоскостью АА1С и прямой ВА1 , если АА1 = 3, АВ = 4, ВС = 4.
Ответ:
arcsin
2 2
.
5
2.5 В кубе ABCDA1B1C1D1 все рёбра равны 1. Найдите расстояние от точки С до
прямой ВD1.
Ответ:
6
.
3
2.6 В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB = 4,
BC = 6, CC1 = 4, найдите тангенс угла между плоскостями CDD1 и BDA1.
3 2
Ответ: 2

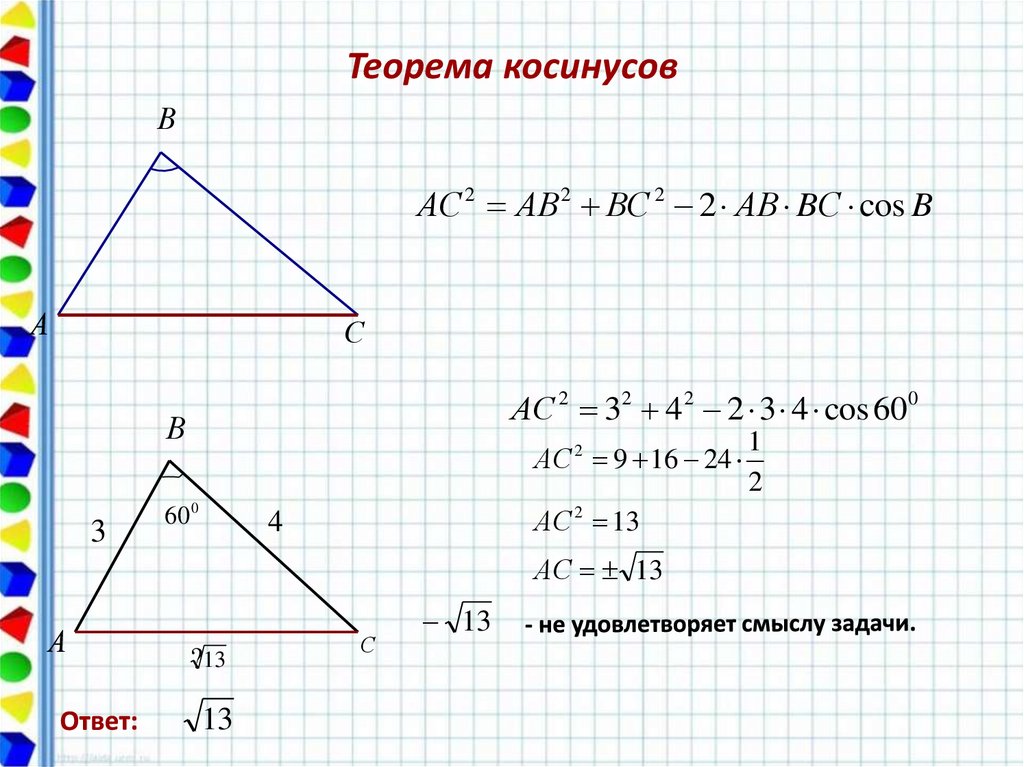
34. Теорема косинусов

В
АС 2 АВ 2 ВС 2 2 АВ BС cos B
А
С
АС 2 32 4 2 2 3 4 cos 600
В
3
АС 2 9 16 24
60 0
АС 2 13
4
АС 13
А
?13
13
С
13
1
2

35.

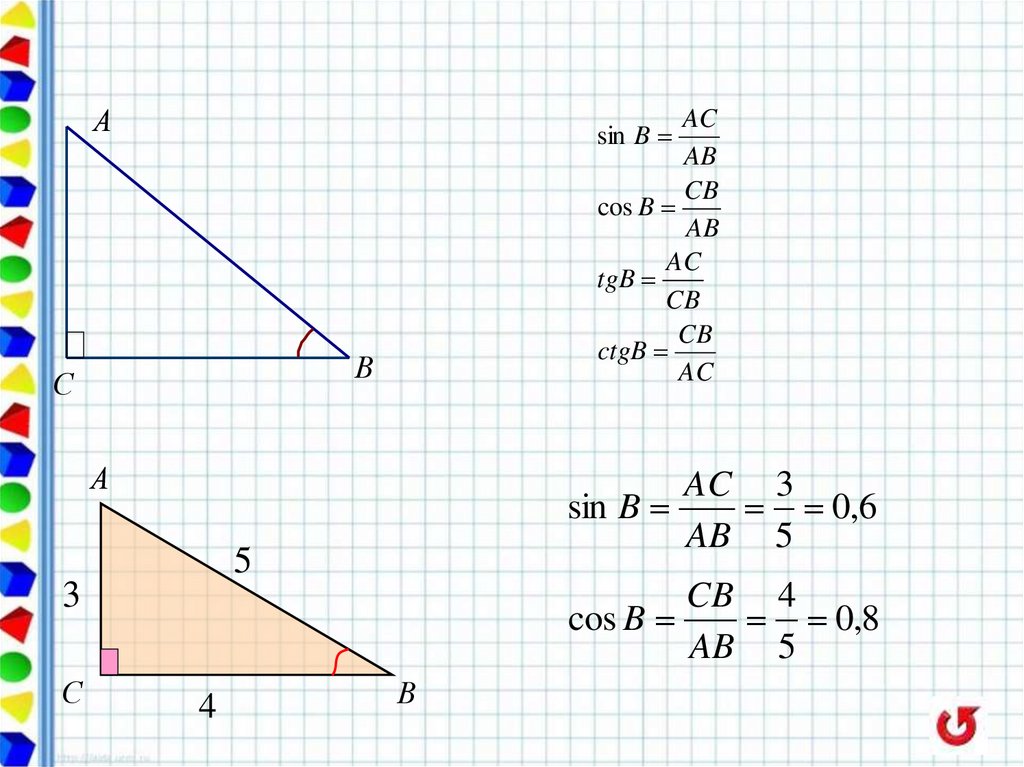
А
AC
AB
CB
cos B
AB
AC
tgB
CB
CB
ctgB
AC
sin B
В
С
А
AC 3
sin B
0,6
AB 5
5
3
С
CB 4
cos B
0,8
AB 5
4
В

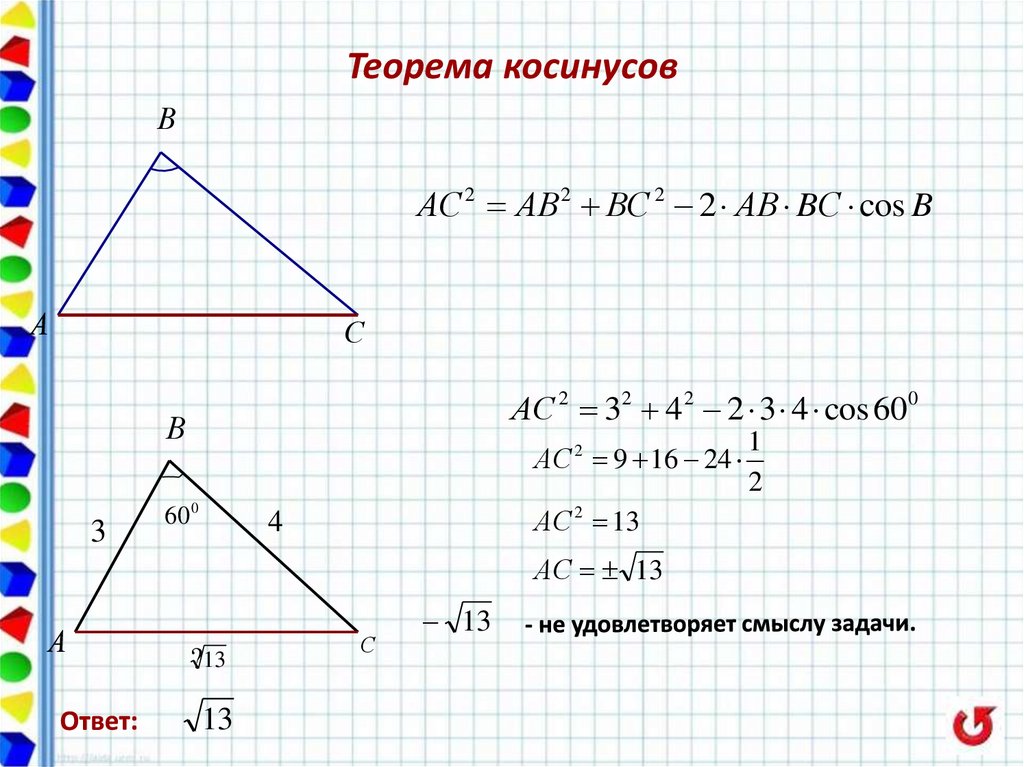
36. Теорема косинусов

В
АС 2 АВ 2 ВС 2 2 АВ BС cos B
А
С
АС 2 32 4 2 2 3 4 cos 600
В
3
АС 2 9 16 24
60 0
АС 2 13
4
АС 13
А
?13
13
С
13
1
2

37.

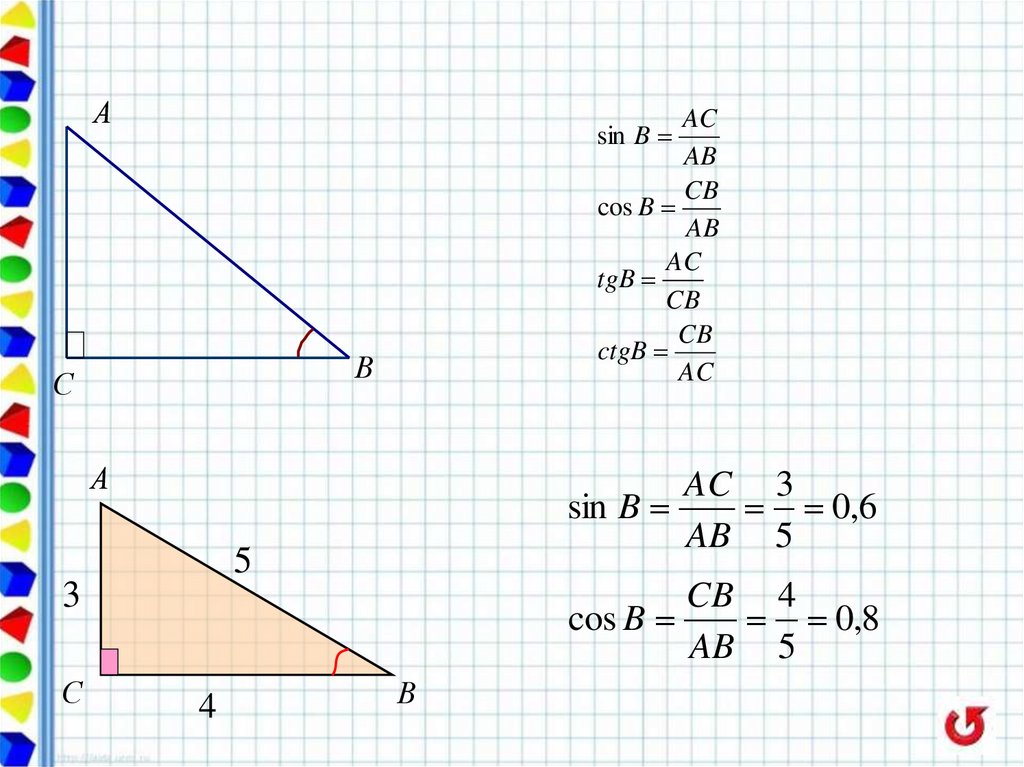
А
AC
AB
CB
cos B
AB
AC
tgB
CB
CB
ctgB
AC
sin B
В
С
А
AC 3
sin B
0,6
AB 5
5
3
С
CB 4
cos B
0,8
AB 5
4
В

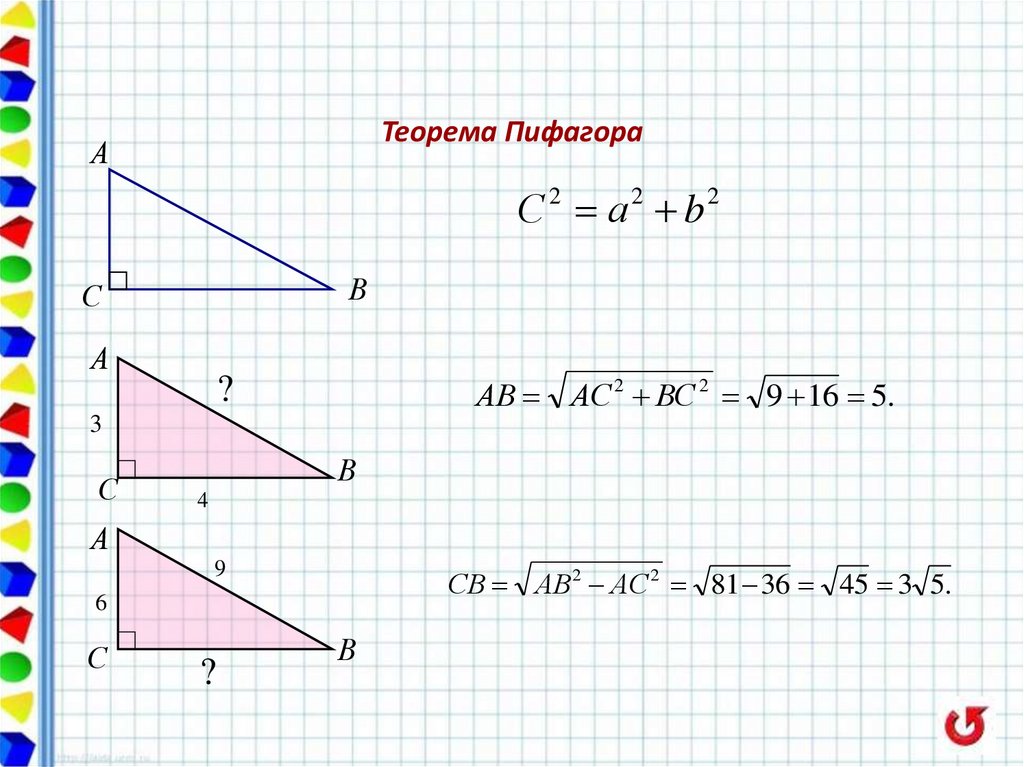
38. Теорема Пифагора

А
С 2 а2 b2
В
С
А
АВ АС 2 ВС 2 9 16 5.
?
3
С
В
4
А
9
СВ АВ2 АС 2 81 36 45 3 5.
6
С
?
В

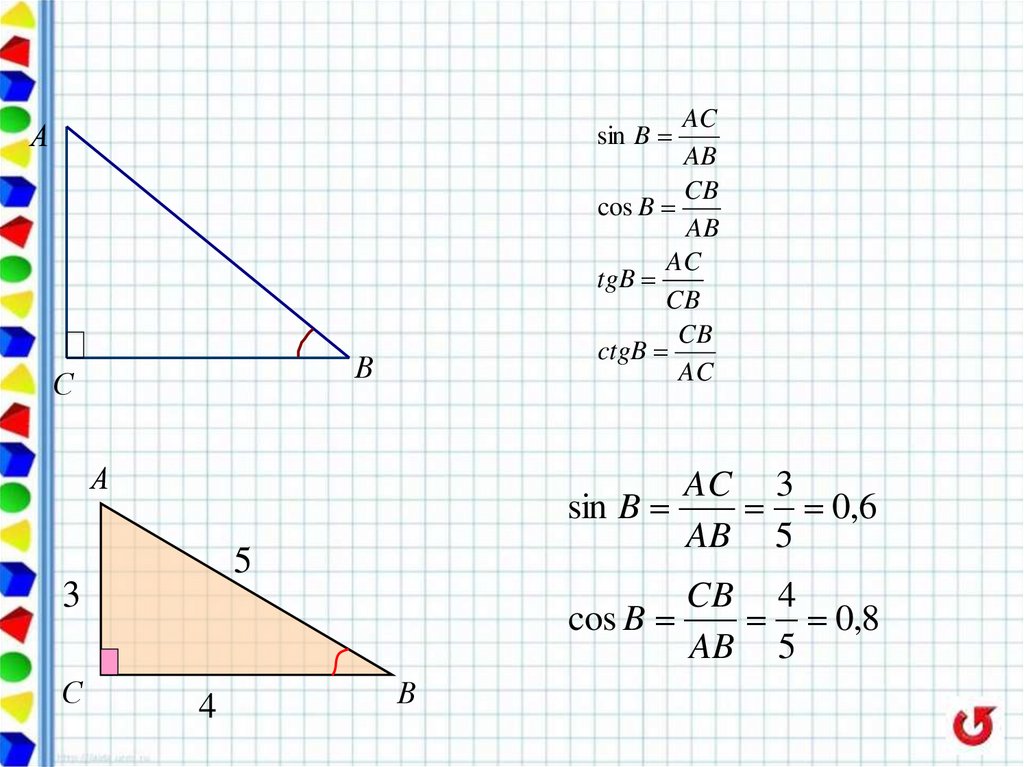
39.

AC
AB
CB
cos B
AB
AC
tgB
CB
CB
ctgB
AC
sin B
А
В
С
А
AC 3
sin B
0,6
AB 5
5
3
С
CB 4
cos B
0,8
AB 5
4
В