Похожие презентации:
Элементы теории вероятностей. Решение текстовых задач на геометрическую вероятность
1.
Элементы теориивероятностей
Решение текстовых задач на
геометрическую вероятность
2.
Задача 1. Выберем на географической карте мира случайнуюточку (например, зажмурим глаза и покажем указкой). Какова
вероятность, что эта точка окажется в Казахстане?
Число исходов бесконечно.
Вероятность будет зависеть от размера карты
(масштаба).
3.
Задача 1. Выберем на географической карте мира случайнуюточку (например, зажмурим глаза и покажем указкой). Какова
вероятность, что эта точка окажется в Казахстане?
S ( A)
P( A)
?
S ( )
Очевидно, для ответа на вопрос нужно знать, какую часть всей
карты занимает Казахстан.
Точнее, какую часть всей площади карты составляет Казахстан.
Отношение этих площадей и даст искомую вероятность.
4.
Общий случай: в некоторой ограниченной области случайновыбирается точка. Какова вероятность, что точка попадет в
область А? На прямую L?
S ( A)
P( A)
S ( )
L
А
0
S ( L) 0; P( L)
0
S ( )
5.
Вероятность попадания точки на территорию Казахстана:Р(А) =
площадь Казахстана на карте .
площадь карты
Вероятность попадания точки на Гринвичский меридиан:
Р(А) =
площадь меридиана = 0.
площадь карты
6.
Геометрическое определение вероятностиЕсли предположить, что попадание в любую точку области
равновозможно, то вероятность попадания случайной точки в заданное
множество А будет равна отношению площадей:
S ( A)
P( A)
S ( )
Если А имеет нулевую площадь, то вероятность попадания в А равна
нулю.
Можно определить геометрическую вероятность в пространстве и на
прямой:
V ( A)
L( A)
P( A)
; P( A)
V ( )
L ( )
7.
№1. Дано: АВ=12см, АМ=2см, МС=4см. На отрезке АВ случайным образомотмечается точка Х. Какова вероятность того, что точка Х попадет на отрезок:
1) АМ; 2) АС; 3)МС; 4) МВ; 5) АВ?
А
М
С
В
Решение.
1) A={точка Х попадает на отрезок АМ}, АМ=2см, АВ=12см,
P ( A)
AM
2 1
AB 12 6
2) В ={точка Х попадает на отрезок АС}, АС=2см+4см=6см,
P( B)
AC 6 1
AB 12 2
3) С ={точка Х попадает на отрезок МС}, МС=4см, АВ=12см,
P (C )
MC
4 1
AB 12 3
4) D={точка Х попадает на отрезок МВ}, МВ=12см–2см=10см,
P( D)
MB 10 5
AB 12 6
5) Е={точка Х попадает на отрезок АВ},
P ( A)
AB
1
AB
8.
№2. Случайным образом выбирают одно из решений неравенства х 1 2Какова вероятность того, что оно являетя и решением неравенства х 0,5 ?
Решение:
1) х 1 2
1;3
длина отрезка 1;3 равна 4.
2) х 0,5
0,5;0,5
длина отрезка 0,5;0,5 равна 1.
1
Р А 0,25
4
Ответ : 25%
9.
№3 На рисунке изображена цель, состоящая изконцентрических кругов с радиусами 1, 3 и 5. Если
известно, что наудачу выстреленная стрела из лука
попадет в эту цель, то найдите вероятность того, что она
попадет в область:
а) закрашенную в красный цвет;
б) закрашенную в зеленый цвет;
в) закрашенную в синий цвет
10.
Решение:2
Площадь большого круга R=5, S R 25
2
среднего круга R=3,
S R 9
2
S R
малого круга R=1,
1
a ) P A
0,04 4%
25 25
9
8
b) P A
0,32 32%
25
25
25 9 16
c ) P A
0,64 64%
25
25
11.
№4. В квадрат со стороной 4 см «бросают» точку. Каковавероятность, что расстояние от этой точки до ближайшей
стороны квадрата будет меньше 1 см?
Закрасим в квадрате множество точек, удаленных от
ближайшей стороны меньше, чем на 1 см.
Площадь закрашенной части квадрата
2 – 4см2 = 12см2.
16см
12 3
P( A) 0,75
Значит,
16 4
12.
№5. Округлите до сотых и используйте 3.14 для π.a.Найдите площадь круга.
b.Найдите площадь квадрата.c.Найти вероятность того, что
брошенный дротик случайно попадет в круг. Дайте ответ в виде
дроби, десятичной дроби и процента.
13.
Решение:a ) S R 3 9
2
2
b) S кв 6 36
2
9 9 3,14 28,26
0,785 78,5%
с ) P A
36
36
36
14.
№6. Прямоугольный треугольник ABC вписан в круг. Известно,что AC = 26, BC = 24, AB = 10. Найти вероятность того, что
случайно брошенный дротик не попадет в треугольник. Дайте
ответ в виде дроби, десятичной дроби и процента.
15.
Решение:2
26
S круга R 169
2
2
1
S треуг 24 10 120
2
Р А
169 120 530,66 120 410,66
0,774 77,4%
169
530,66
530,66
16.
№7. Оконная решетка состоит из клеток со стороной 20см. Врешетку 100 раз бросили наугад один и тот же мяч. В 50
случаях он пролетел через решетку не задев ее. Оцените
приближенно радиус мяча.
Решение.
NA
50
1
P ( A)
N
100
2
S мяча
R 2
P ( A)
S кв
400
R 2
1
400
2
400
200
2
R
2
200
2
R
10
4,5(см)
17.
Рефлексия: оцените свои знания по теме«Геометрическая вероятность» попаданием в цель.
Наклейте стикер на соответствующую область














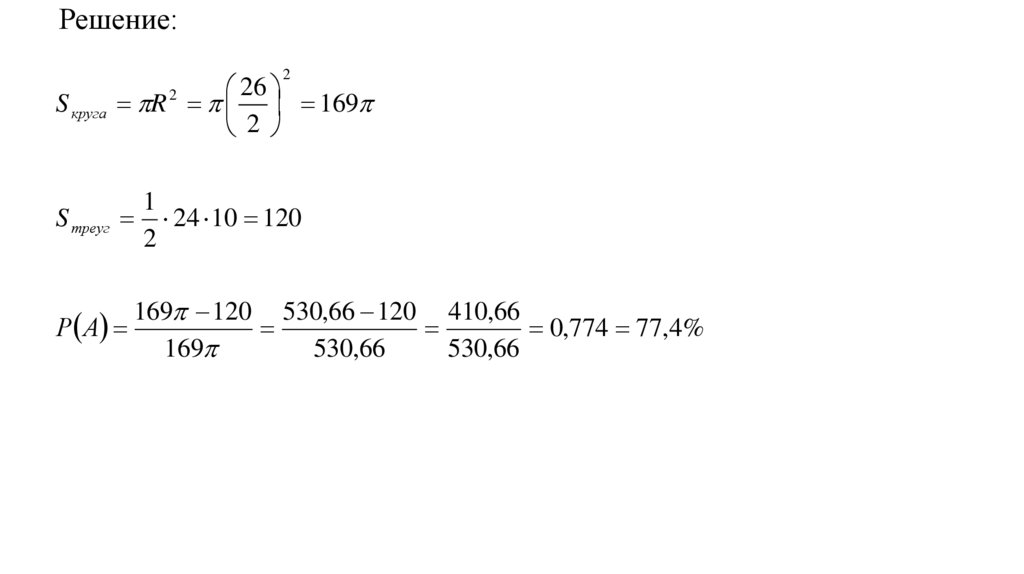


 Математика
Математика








