ec17f2219f7845628824d8fafcc466fc

1.

2.

Геометрическая
вероятность

3.

Закрепление материала
по теме :
«Геометрическая
вероятность».

4.

Повторение понятий
Закрепление материала
решением задач
Тест
Задачи повышенной сложности
Домашняя работа

5.

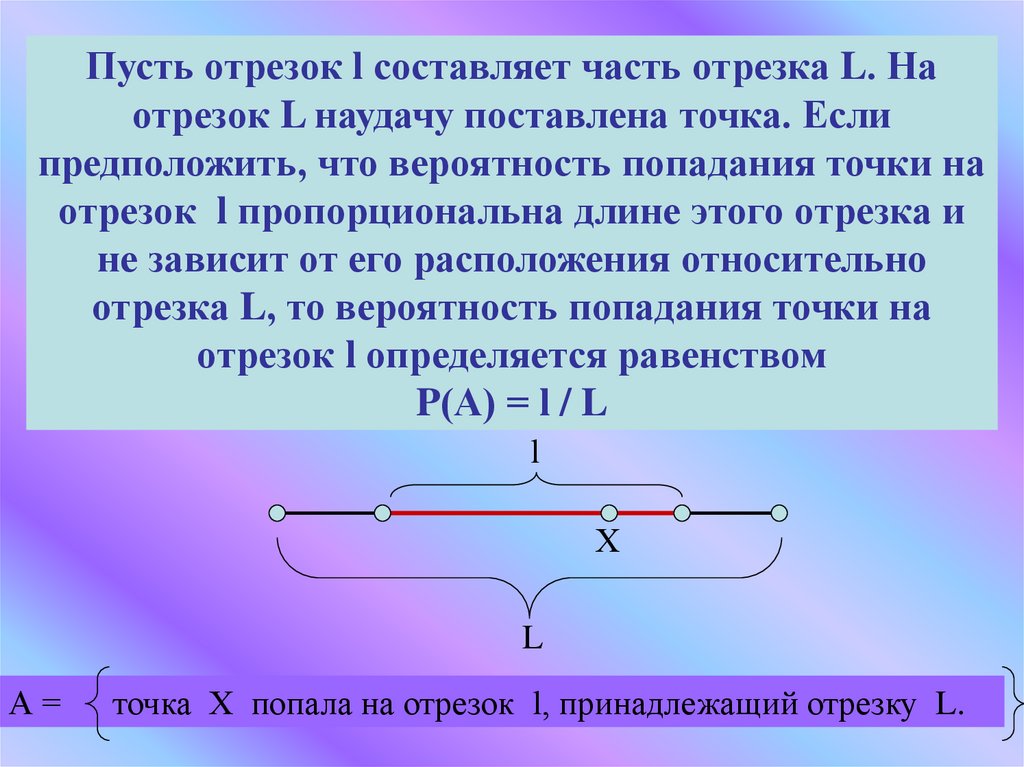
Пусть отрезок l составляет часть отрезка L. На
отрезок L наудачу поставлена точка. Если
предположить, что вероятность попадания точки на
отрезок l пропорциональна длине этого отрезка и
не зависит от его расположения относительно
отрезка L, то вероятность попадания точки на
отрезок l определяется равенством
P(А) = l / L
l
Х
L
А=
точка Х попала на отрезок l, принадлежащий отрезку L.

6.

Пусть плоская фигура g составляет часть плоской
фигуры G. На фигуру G наудачу брошена точка.
Если предположить, что вероятность попадания
брошенной точки на фигуру g пропорциональна
площади этой фигуры и не зависит ни от ее
расположения относительно G, ни от формы g, то
вероятность попадания точки в фигуру g
определяется равенством
Р(А) = S g / S G
G
Х
g
А = точка Х попала на фигуру g ,
составляющую часть плоской фигуры G.

7.

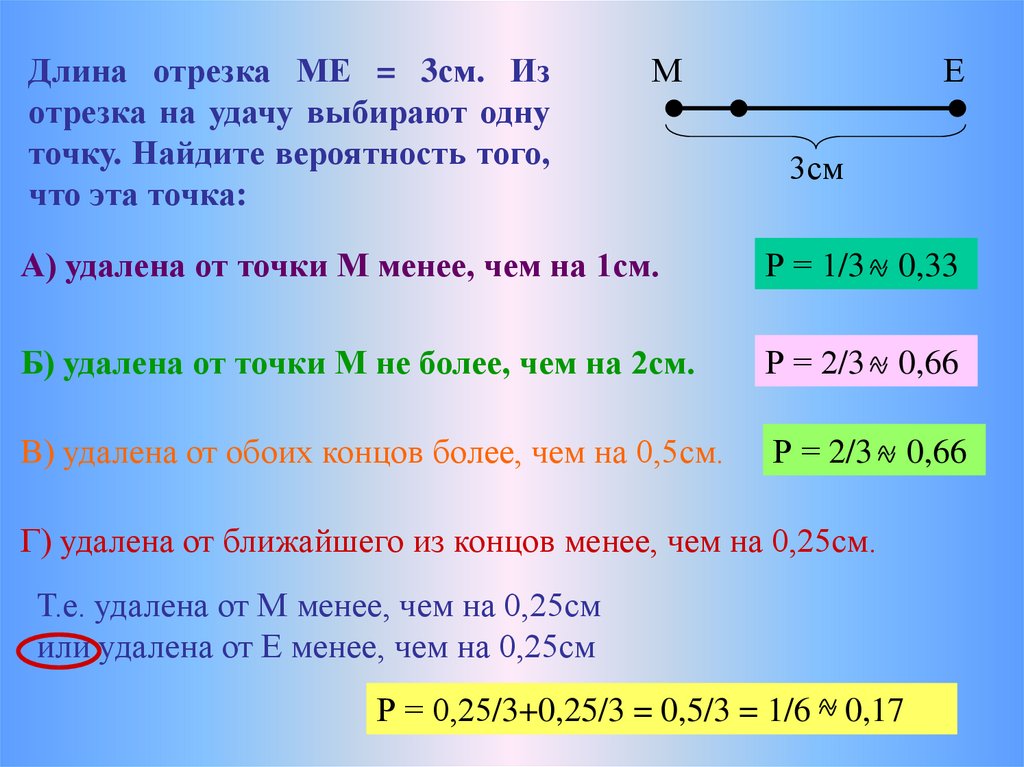
Длина отрезка МЕ = 3см. Из
отрезка на удачу выбирают одну
точку. Найдите вероятность того,
что эта точка:
М
Е
3см
А) удалена от точки М менее, чем на 1см.
Р = 1/3 0,33
Б) удалена от точки М не более, чем на 2см.
Р = 2/3 0,66
В) удалена от обоих концов более, чем на 0,5см.
Р = 2/3 0,66
Г) удалена от ближайшего из концов менее, чем на 0,25см.
Т.е. удалена от М менее, чем на 0,25см
или удалена от Е менее, чем на 0,25см
Р = 0,25/3+0,25/3 = 0,5/3 = 1/6 0,17

8.

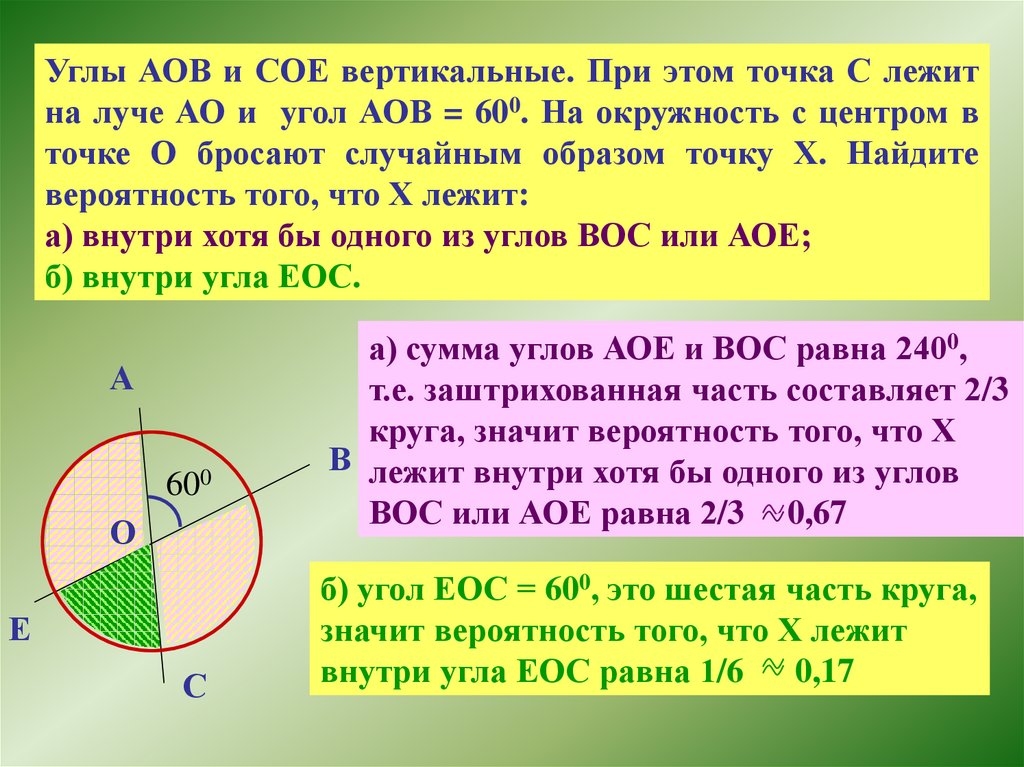
Углы АОВ и СОЕ вертикальные. При этом точка С лежит
на луче АО и угол АОВ = 600. На окружность с центром в
точке О бросают случайным образом точку Х. Найдите
вероятность того, что Х лежит:
а) внутри хотя бы одного из углов ВОС или АОЕ;
б) внутри угла ЕОС.
А
600
О
Е
С
а) сумма углов АОЕ и ВОС равна 2400,
т.е. заштрихованная часть составляет 2/3
круга, значит вероятность того, что Х
В лежит внутри хотя бы одного из углов
ВОС или АОЕ равна 2/3 0,67
б) угол ЕОС = 600, это шестая часть круга,
значит вероятность того, что Х лежит
внутри угла ЕОС равна 1/6 0,17

9.

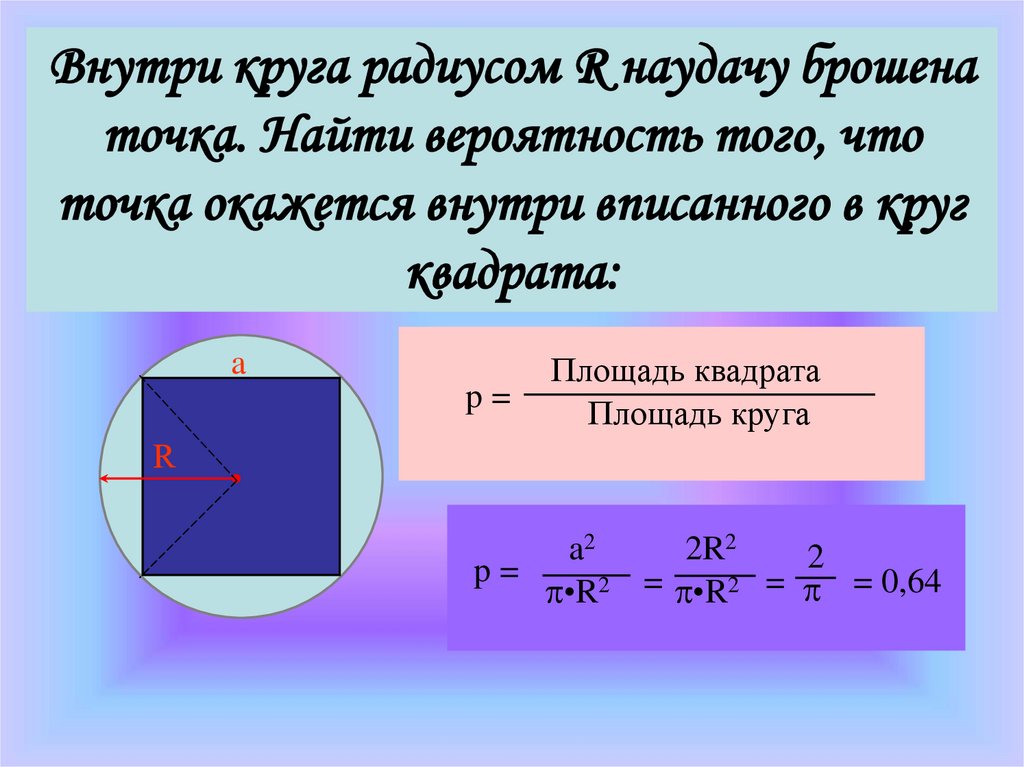
Внутри круга радиусом R наудачу брошена
точка. Найти вероятность того, что
точка окажется внутри вписанного в круг
квадрата:
a
p=
Площадь квадрата
Площадь круга
a2
2R2
2
p=
•R2 = •R2 = = 0,64

10.

В прямоугольник случайным образом бросается точка.
Найдите вероятность события:
а) А={точка принадлежит ромбу, вершинами которого
служат середины сторон прямоугольника},
б) В={точка принадлежит треугольнику, вершинами
которого служат две соседние вершины прямоугольника и
точка пересечения его диагоналей}.
Х
а) Р(А) = 0,5
Х
б) Р(В) = 0,25

11.

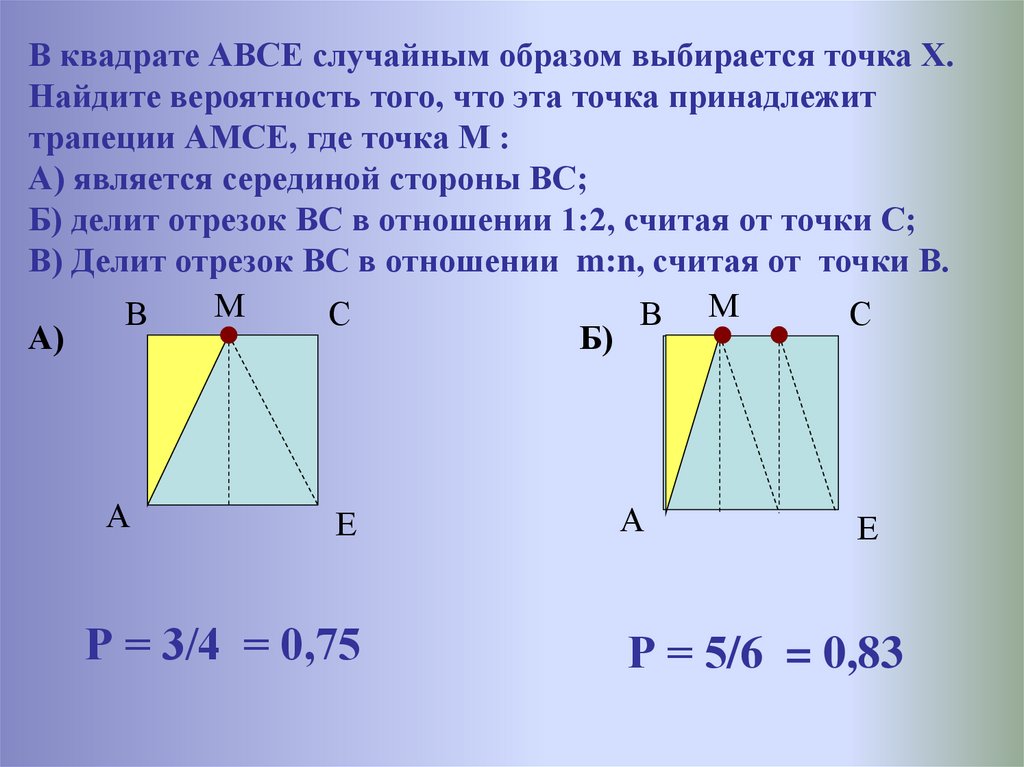
В квадрате АВСЕ случайным образом выбирается точка Х.
Найдите вероятность того, что эта точка принадлежит
трапеции АМСЕ, где точка М :
А) является серединой стороны ВС;
Б) делит отрезок ВС в отношении 1:2, считая от точки С;
В) Делит отрезок ВС в отношении m:n, считая от точки В.
М
В
С
В М
С
А)
Б)
А
Е
Р = 3/4 = 0,75
А
Е
Р = 5/6 = 0,83

12.

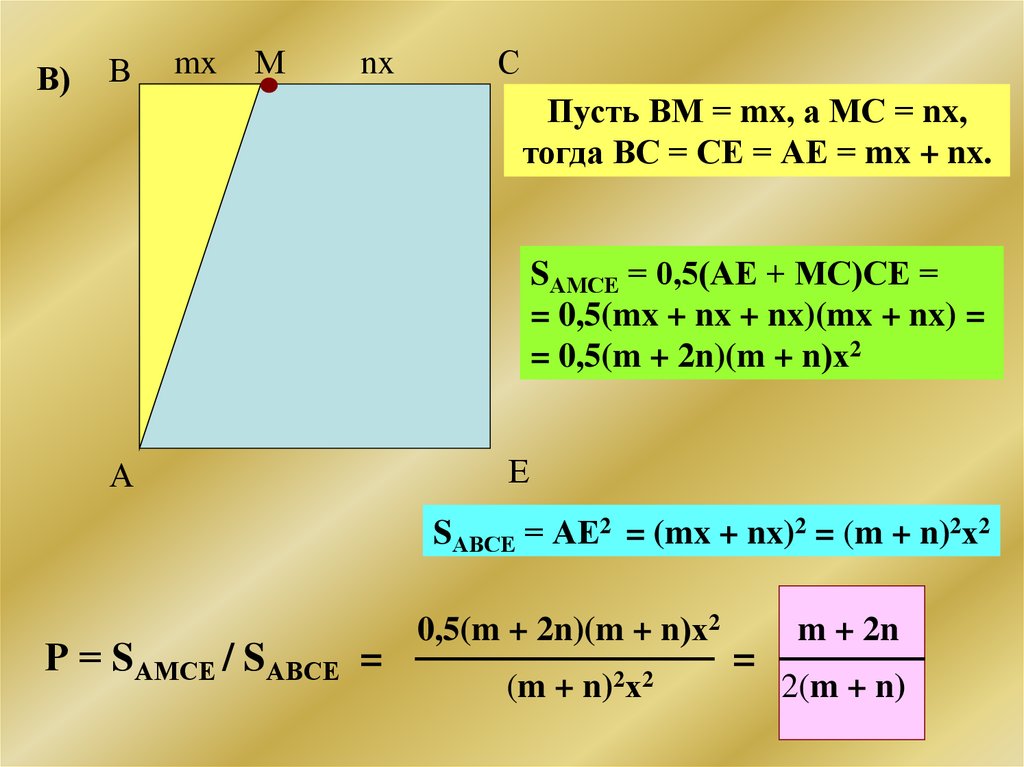
В)
В
mx
М
nx
С
Пусть ВМ = mx, а МС = nx,
тогда ВС = СЕ = АЕ = mx + nx.
SАМСЕ = 0,5(АЕ + МС)СЕ =
= 0,5(mx + nx + nx)(mx + nx) =
= 0,5(m + 2n)(m + n)х2
А
Е
SАВСЕ = АЕ2 = (mx + nx)2 = (m + n)2х2
Р = SАМСЕ / SАВСЕ =
0,5(m + 2n)(m + n)х2
(m + n)2х2
=
m + 2n
2(m + n)

13. Поговорим немного о здоровье

• Человек,
заботящийся
о
своем
здоровье обязательно выполняет все
правила дорожного движения
• Вспомним о правилах перехода через
улицу

14.

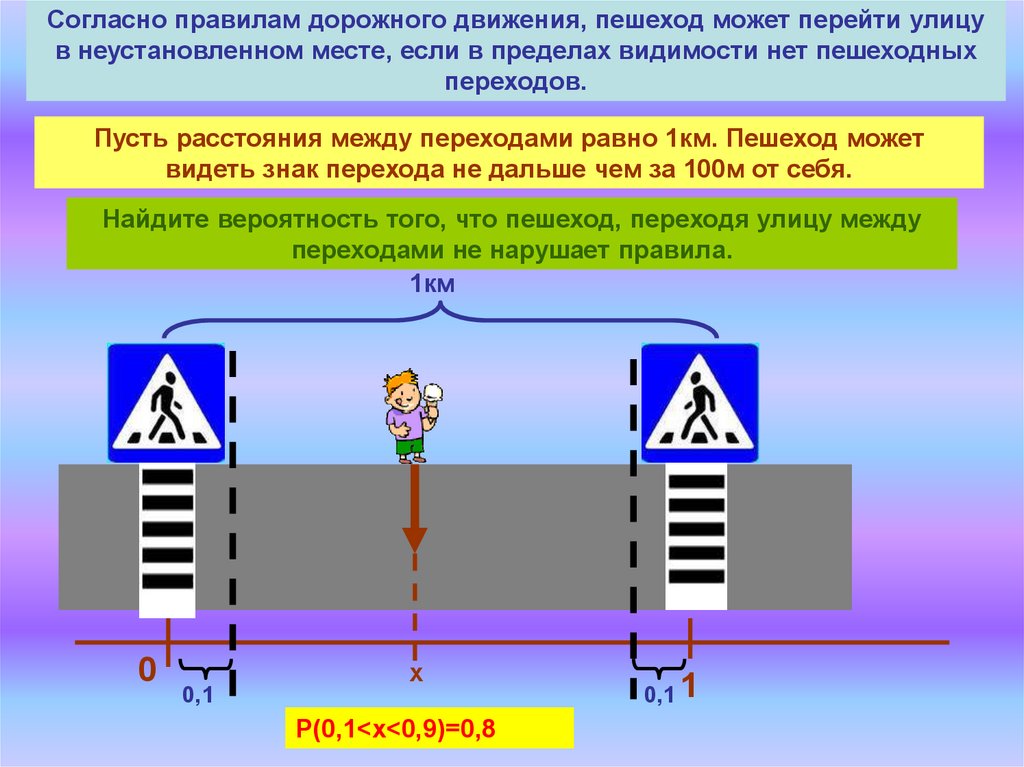
Согласно правилам дорожного движения, пешеход может перейти улицу
в неустановленном месте, если в пределах видимости нет пешеходных
переходов.
Пусть расстояния между переходами равно 1км. Пешеход может
видеть знак перехода не дальше чем за 100м от себя.
Найдите вероятность того, что пешеход, переходя улицу между
переходами не нарушает правила.
1км
0
0,1
х
Р(0,1<х<0,9)=0,8
0,1 1

15.

16.

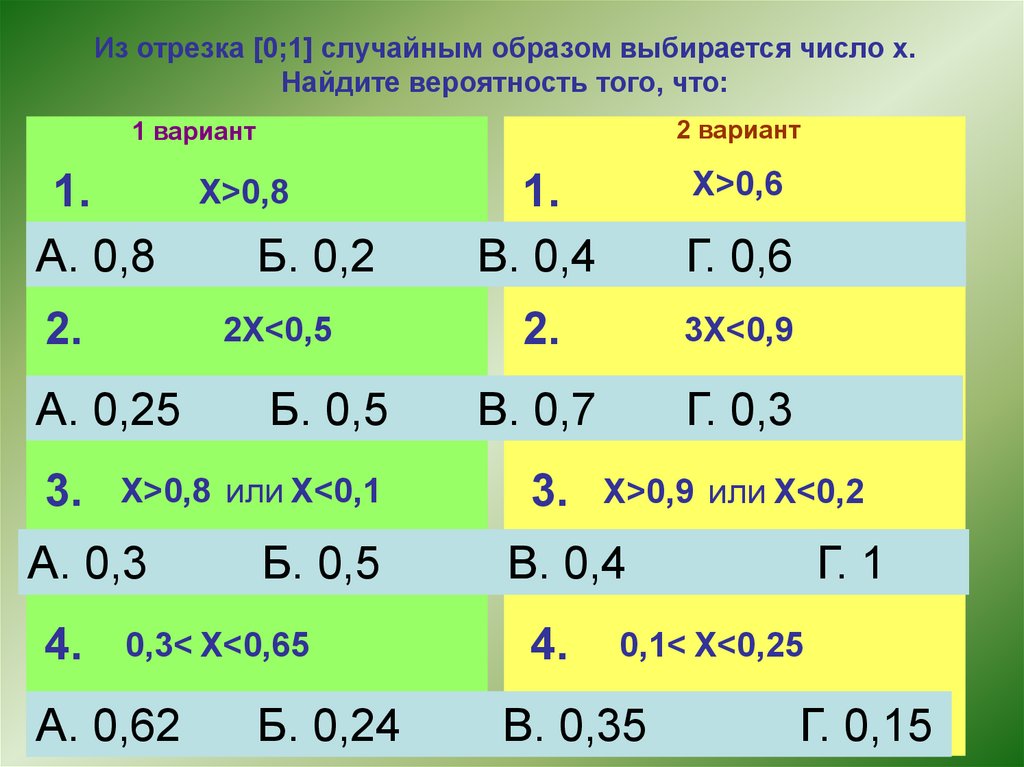
Из отрезка [0;1] случайным образом выбирается число х.
Найдите вероятность того, что:
2 вариант
1 вариант
1.
А. 0,8
А. 0,25
Б. 0,5
Х>0,8 или Х<0,1
А. 0,3
4.
Б. 0,2
2Х<0,5
2.
3.
Х>0,8
Б. 0,5
0,3< Х<0,65
А. 0,62
Б. 0,24
Х>0,6
1.
В. 0,4
Г. 0,6
2.
3Х<0,9
В. 0,7
Г. 0,3
3.
Х>0,9 или Х<0,2
В. 0,4
4.
Г. 1
0,1< Х<0,25
В. 0,35
Г. 0,15

17.

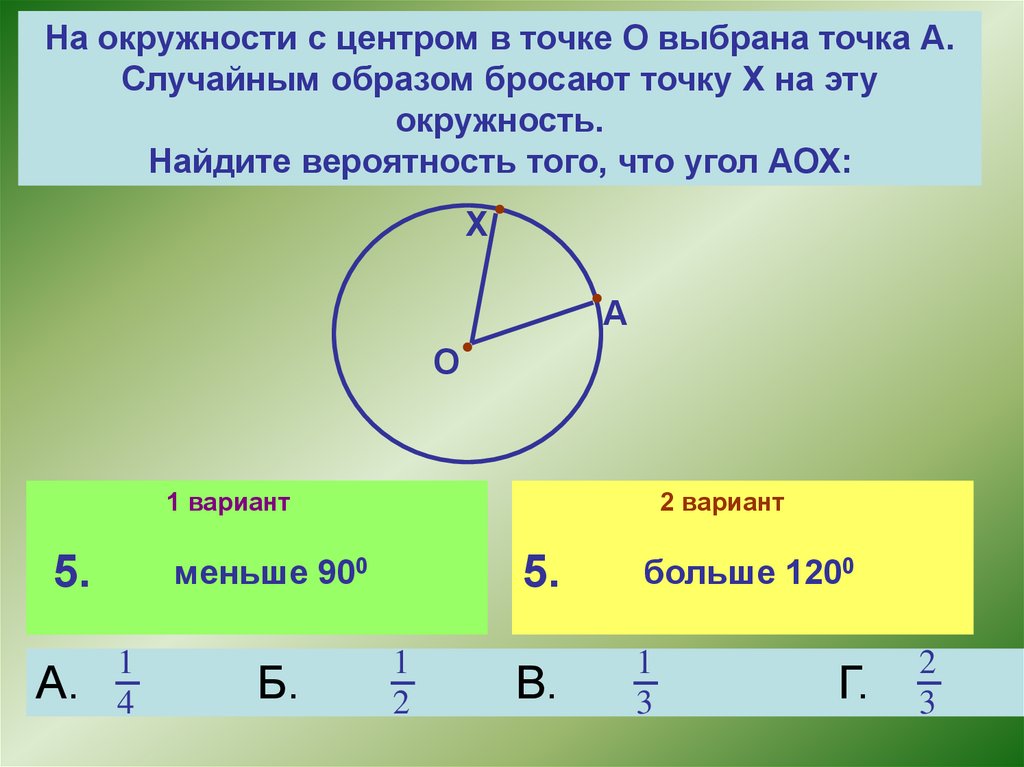
На окружности с центром в точке О выбрана точка А.
Случайным образом бросают точку Х на эту
окружность.
Найдите вероятность того, что угол АОХ:
Х
А
О
1 вариант
меньше 900
5.
А.
2 вариант
1
4
Б.
1
2
5.
больше 1200
В.
1
3
Г.
2
3

18.

Буратино посадил в центре прямоугольного листа
размером 20см на 25см круглую кляксу радиусом 1 см.
Сразу же после этого Буратино посадил еще одну такую
же кляксу, которая также целиком оказалась на листе.
Найдите вероятность того, что эти две кляксы не
соприкасаются.

19.

Для этого центр
второй кляксы
должен находиться
внутри круга с
центром первой
кляксы и радиусом
2см.
Что бы найти
вероятность этого
события, нужно
площадь круга
разделить на площадь
всего листа бумаги
p=
•R2
ab
•22
= 20•25 = 125
Будем решать задачу от обратного.
Найдем вероятность того, что
кляксы будут соприкасаться.
2см
1см
Тогда вероятность того, что
кляксы не будут
соприкасаться равна
1- 125 = 0,98

20.

В круг радиуса R вписан правильный треугольник. Внутрь
круга наугад брошены четыре точки. Найти вероятности
следующих событий:
а) все четыре точки попадут внутрь треугольника;
б) одна точка попадет внутрь треугольника и по одной точке
попадет на каждый «малый сегмент».
Решение:
а) Найдем вероятность попадания всех точек в треугольник.
a
R=
3
Sтреугольника =
Sкруга=
а2
3
4
П R2
3R2 3
=
4
Вероятность
Sтреугольника
попадания одной точки
3R2 3
Р = Sкруга =
в треугольник равна:
4П R2
Вероятность попадания четырех
точек в треугольник равна:
(
3 3
4П
=
)4
3 3
4П
0,41
0,029

21.

б) Найдем вероятность, что одна точка
попадет внутрь треугольника и по одной
точке попадет на каждый «малый сегмент».
Вероятность попадания одной точки 3 3
4П
в треугольник равна:
Sсегмента= (Sкруга- Sтреугольника)/3= (
П R2 -
3R2
3 )/3=
4П R2 -3R2
0,41
3
4
12
Вероятность попадания одной точки в сегмент равна:
4П R2 -3R2 3
4П - 3 3
Sодного сегмента
Р = Sкруга
=
=
0,2
2
12 П
12 П R
Вероятность попадания по одной точке на каждый
сегмент равна:
Искомая вероятность Р = 3!
3 3
4П
4П - 3
4П - 3
( 12 П )
0,008
3 3
( 12 П )
3 3
0,02

22.

На отрезке АО длины
L числовой оси Ох наудачу
поставлены две точки: В(х) и С(у). Найти вероятность того,
что из трех получившихся отрезков можно построить
треугольник.
того чтобы из трех отрезков
у
Решение: Для
можно было построить треугольник,
L
D
каждый из отрезков должен быть
меньше суммы двух других.
Сумма всех трех отрезков равна L,
поэтому каждый из отрезков должен
быть меньше L/2.
М(х ; у)
О
L
Введем в рассмотрение прямоугольную
систему координат хОу. Координаты любых
двух точек В и С должны удовлетворять
х двойным неравенствам:
0 < х < L,
0 < у < L.
Этим неравенствам удовлетворяют координаты любой точки М(х ; у),
принадлежащей квадрату ОLDL. Таким образом этот квадрат можно
рассматривать как фигуру G, координаты точек которой представляют все
возможные значения координат точек В и С.

23.

L
0
В(х) С(у)
ОВ < L/2,
ВС < L/2,
СА < L/2.
или
А
1. Пусть точка С расположена
правее точки В.
Как указано выше должны
х выполняться неравенства:
х < L/2,
у – х < L/2,
L - у < L/2.
или
х < L/2,
у < х + L/2,
у > L/2.
L
0
С(у) В(х)
ОС < L/2,
ВС < L/2,
ВА < L/2.
или
А
х
у < L/2,
х – у< L/2,
L - х < L/2.
2. Пусть точка С расположена
левее точки В.
Тогда
должны
выполняться
неравенства:
или
у < L/2,
у > х - L/2,
х > L/2.

24.

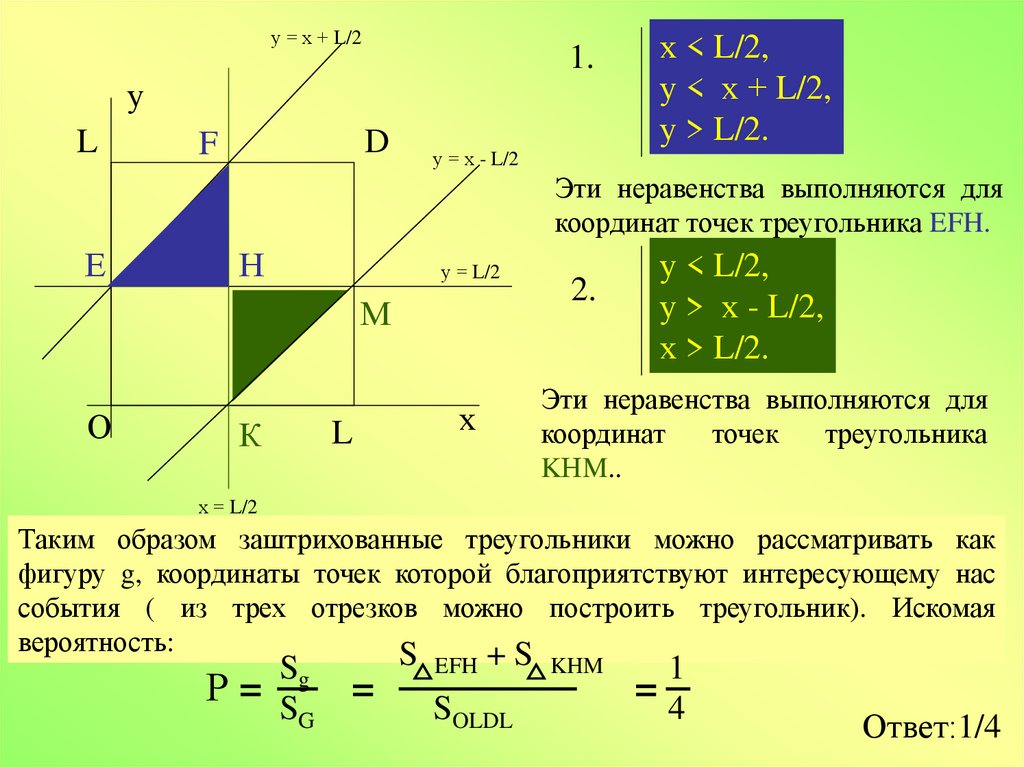
у = х + L/2
1.
у
L
D
F
х < L/2,
у < х + L/2,
у > L/2.
у = х - L/2
Эти неравенства выполняются для
координат точек треугольника EFH.
Е
Н
у = L/2
М
О
К
L
х
2.
у < L/2,
у > х - L/2,
х > L/2.
Эти неравенства выполняются для
координат
точек
треугольника
KНM..
х = L/2
Таким образом заштрихованные треугольники можно рассматривать как
фигуру g, координаты точек которой благоприятствуют интересующему нас
события ( из трех отрезков можно построить треугольник). Искомая
вероятность:
S
+S
S
Р = Sg
G
=
EFH
SOLDL
KHM
1
=4
Ответ:1/4

25.

№2
В сигнализатор поступают сигналы от двух устройств, причем
поступление каждого из сигналов равно возможно в любой момент
промежутка времени длительностью Т. Моменты поступления сигналов
независимы один от другого. Сигнализатор срабатывает, если разность
между моментами поступления сигналов меньше t (t < T). Найдите
вероятность того, что сигнализатор срабатывает за время Т, если каждое
из устройств пошлет по одному из сигналов.
Обозначим моменты поступления сигналов
первого и второго устройств через х и у
соответственно. В силу условия задачи:
Решение:
у
Т
0 < х < Т,
0 < у < Т.
А
Введем в рассмотрение прямоугольную систему
координат хОу. Точки квадрата ОТАТ удовлетворяют
данным неравенствам. Этот квадрат можно
рассматривать как фигуру G, координаты точек
которой представляют все возможные значения
моментов поступления сигналов.
О
Т
х

26.

Сигнализатор срабатывает, если разность между
моментами поступления сигналов меньше t, т.е.,
если у –х < t при у > х и х – у < t при х > у,
или, что то же,
у < х + t при у > х,
у > х - t при у < х.
Как видно из рисунка, все точки, координаты которых удовлетворяют этим
неравенствам принадлежат заштрихованному шестиугольнику. Таким
образом, этот шестиугольник можно рассматривать как фигуру g,
координаты точек которой являются благоприятствующими срабатыванию
сигнализатора моментами времени х и у.
Искомая вероятность:
S
Р = Sg
G
=
Т2 -2( Т - t )2/2
Т2
=
t(2Т –t)
Т2