Похожие презентации:
Поверхности. Лекция 5
1.
ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТКАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
Лекция 5
Тема: Поверхности
РАЗРАБОТАЛИ: ст. преп. кафедры Н Г и Г – Крамаровская В.И.
ст. преп. кафедры Н Г и Г – Стаселько О.Л.
ст. преп. кафедры Н Г и Г – Шушарина И.В.
2.
Способы задания поверхностиСуществует несколько способов задания поверхности:
1. Аналитический (поверхность в этом случае задана уравнением);
2. Задание поверхности каркасом;
Например, земная поверхность задается каркасом (семейством
горизонталей), или поверхность самолета, автомобиля (сложные
поверхности);
3. Кинематический (поверхности рассматриваются как множество
последовательных положений движущейся линии).
3.
Поверхность – это совокупность последовательных положений линии,перемещающихся в пространстве по определенному закону.
• Образующая – линия (прямая или кривая), которая движется в пространстве и
создаёт поверхность.
• Направляющая – линия (или линии), по которой перемещается образующая.
Образующая, как и направляющая, может быть не одна. Это может быть
одна кривая линия и одна прямая линия, может быть две прямые линии, может
быть две кривые линии, может быть несколько кривых или прямых линий.
l – образующая
l
n – направляющая
n
4.
• Чтобы задать поверхность на чертеже, достаточно иметь на немтакие элементы поверхности, которые позволяют построить
каждую ее точку. Совокупность основных параметров
поверхности, которые определяют ее задание называется
определителем поверхности.
Одна и та же поверхность может быть образована различными
способами.
5.
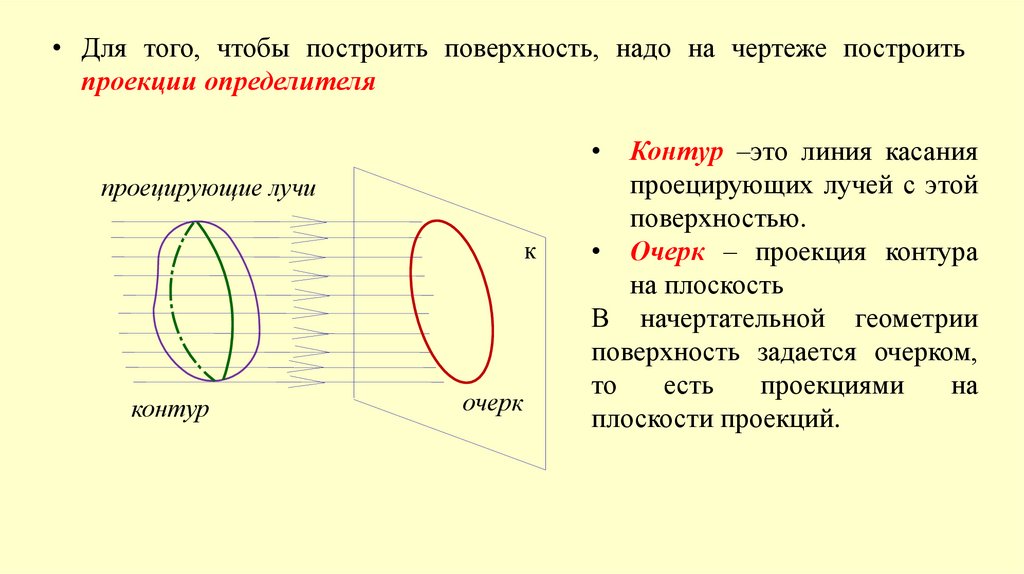
• Для того, чтобы построить поверхность, надо на чертеже построитьпроекции определителя
проецирующие лучи
к
контур
очерк
Контур –это линия касания
проецирующих лучей с этой
поверхностью.
• Очерк – проекция контура
на плоскость
В начертательной геометрии
поверхность задается очерком,
то
есть
проекциями
на
плоскости проекций.
6.
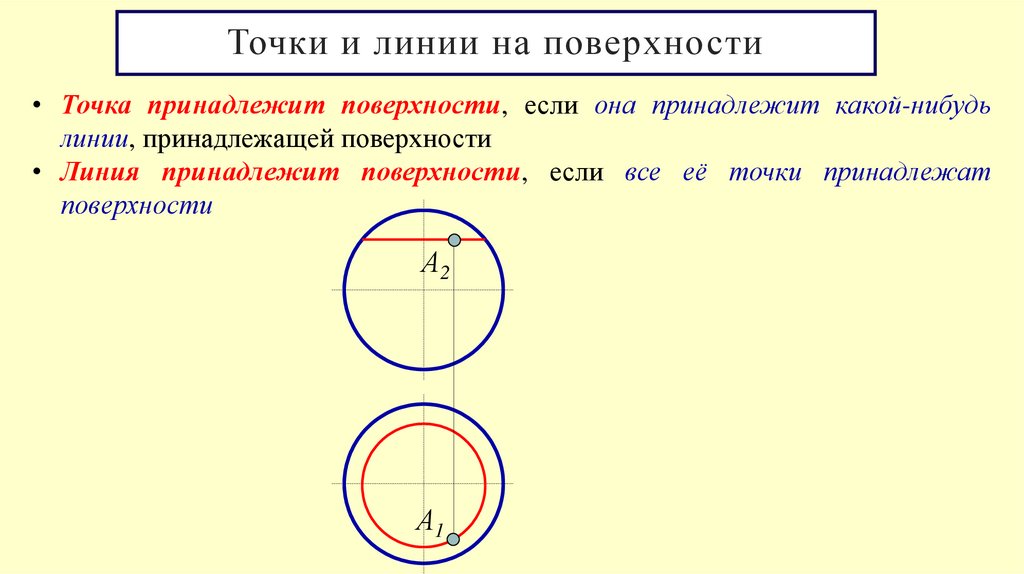
Точки и линии на поверхности• Точка принадлежит поверхности, если она принадлежит какой-нибудь
линии, принадлежащей поверхности
• Линия принадлежит поверхности, если все её точки принадлежат
поверхности
А2
А1
7.
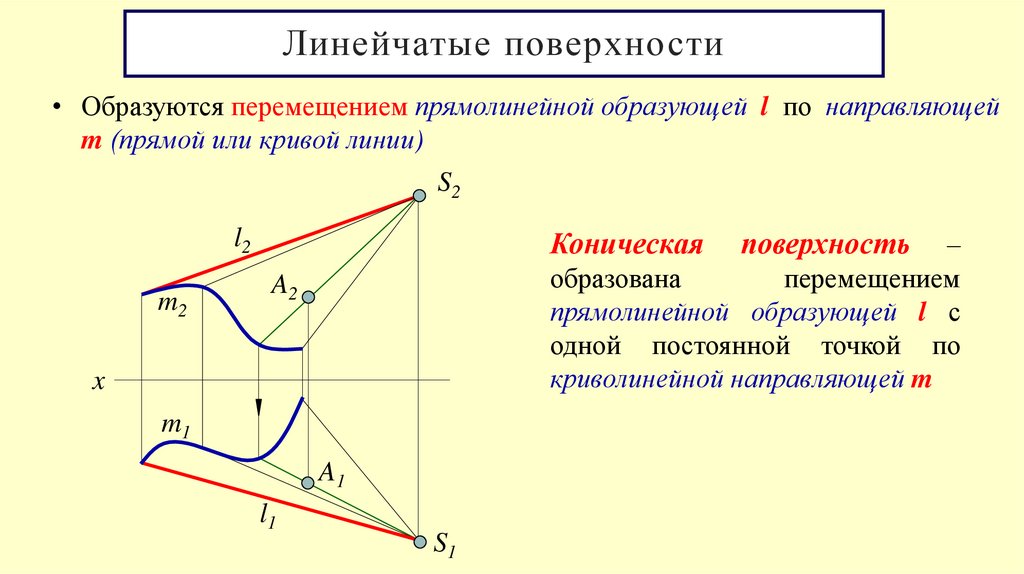
Линейчатые поверхности• Образуются перемещением прямолинейной образующей l по направляющей
m (прямой или кривой линии)
S2
Коническая
l2
m2
–
образована
перемещением
прямолинейной образующей l с
одной постоянной точкой по
криволинейной направляющей m
A2
x
m1
A1
l1
поверхность
S1
8.
l2A2
m2
x
m1
A1
l1
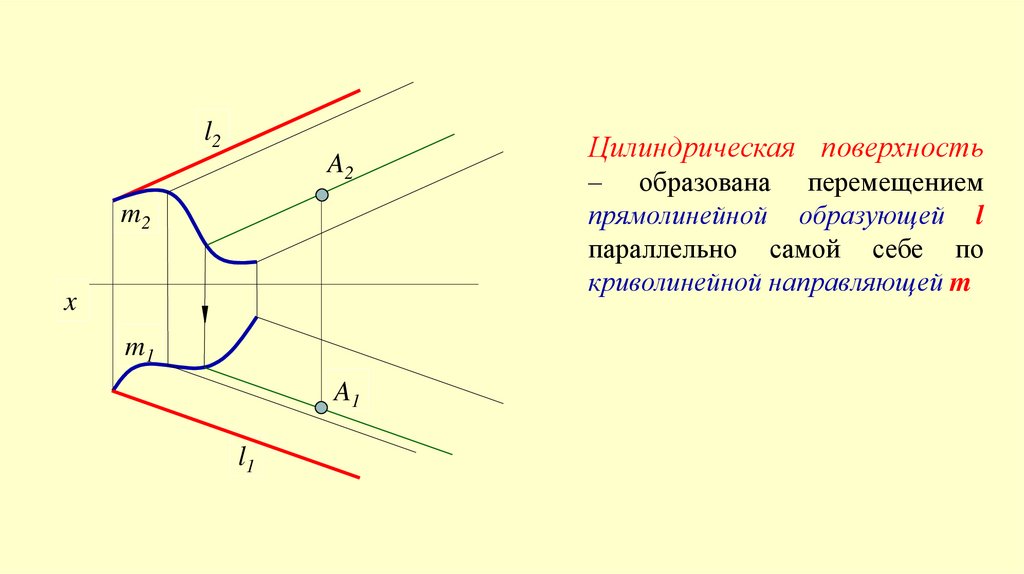
Цилиндрическая поверхность
– образована перемещением
прямолинейной образующей l
параллельно самой себе по
криволинейной направляющей m
9.
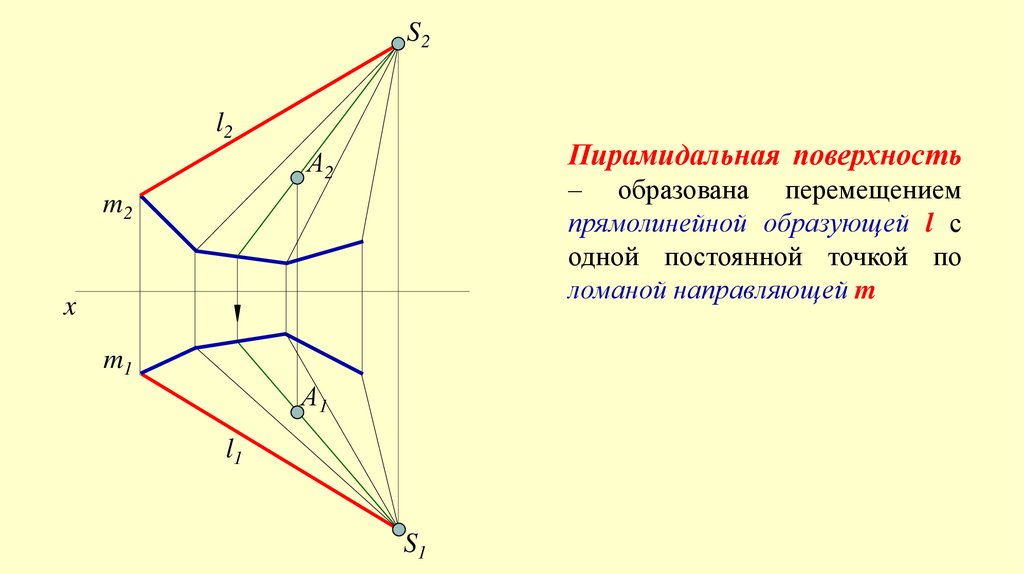
S2l2
Пирамидальная поверхность
А2
– образована перемещением
прямолинейной образующей l с
одной постоянной точкой по
ломаной направляющей m
m2
x
m1
А1
l1
S1
10.
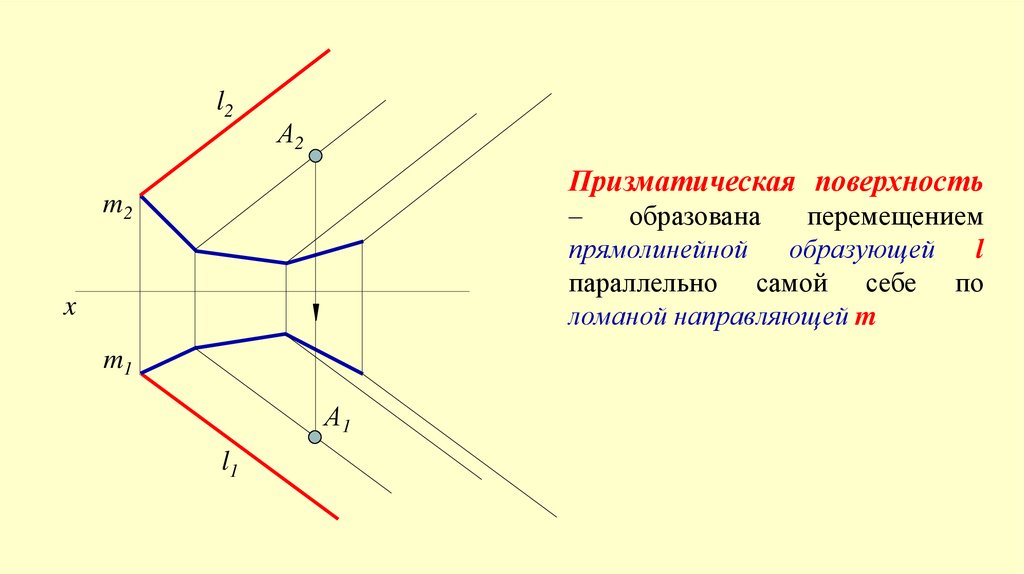
l2А2
Призматическая поверхность
m2
–
образована
перемещением
прямолинейной образующей l
параллельно самой себе по
ломаной направляющей m
x
m1
А1
l1
11.
МногогранникиМногогранная поверхность – это поверхность, ограниченная
отсеками (частями плоскостей)
Эти отсеки называются гранями, пересечение граней – рёбра,
пересечение рёбер – вершины
12.
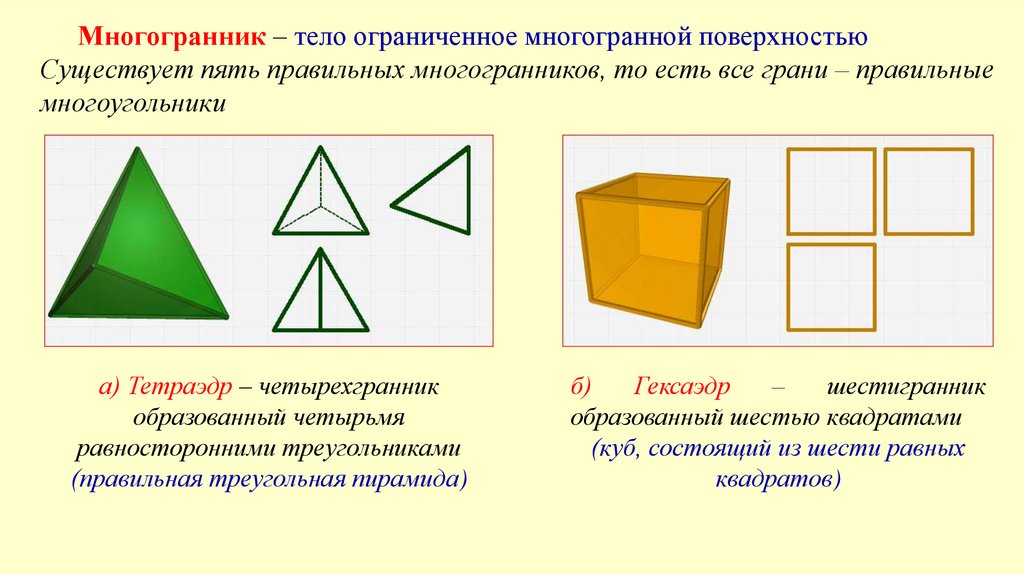
Многогранник – тело ограниченное многогранной поверхностьюСуществует пять правильных многогранников, то есть все грани – правильные
многоугольники
а) Тетраэдр – четырехгранник
образованный четырьмя
равносторонними треугольниками
(правильная треугольная пирамида)
б)
Гексаэдр
–
шестигранник
образованный шестью квадратами
(куб, состоящий из шести равных
квадратов)
13.
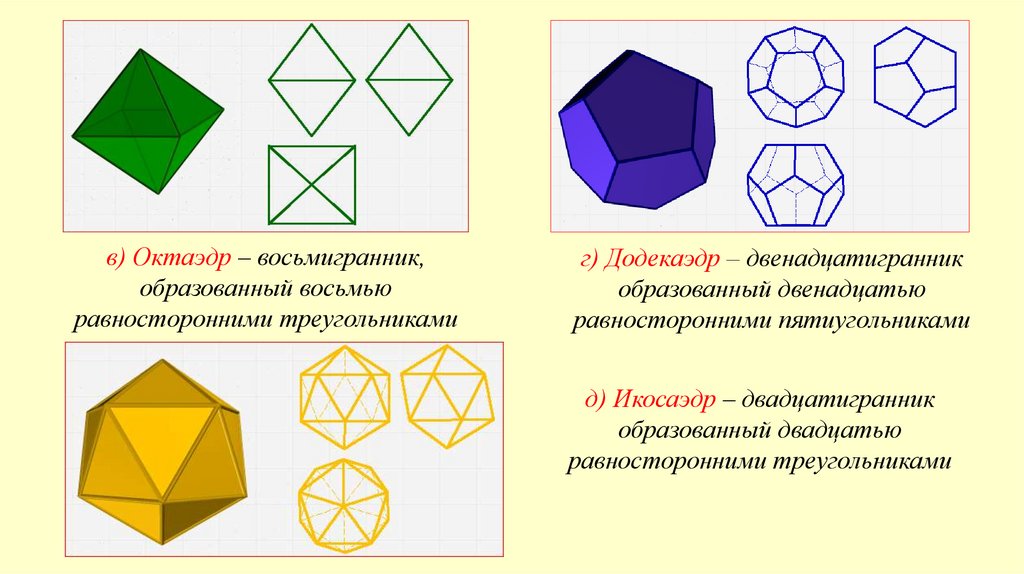
в) Октаэдр – восьмигранник,образованный восьмью
равносторонними треугольниками
г) Додекаэдр – двенадцатигранник
образованный двенадцатью
равносторонними пятиугольниками
д) Икосаэдр – двадцатигранник
образованный двадцатью
равносторонними треугольниками
14.
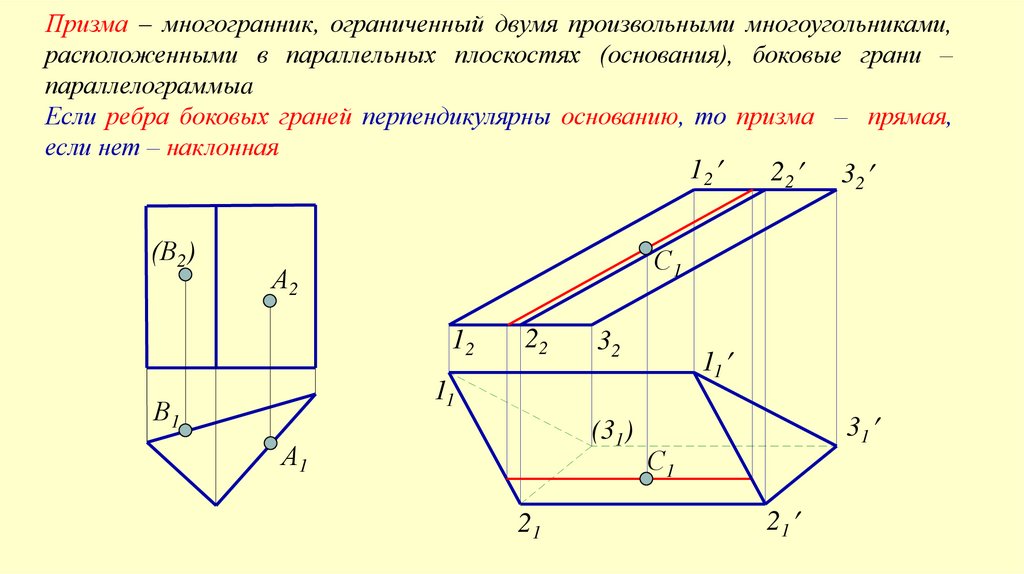
Призма – многогранник, ограниченный двумя произвольными многоугольниками,расположенными в параллельных плоскостях (основания), боковые грани –
параллелограммыa
Если ребра боковых граней перпендикулярны основанию, то призма – прямая,
если нет – наклонная
1 2
(В2)
32
С1
А2
12
22
32
11
11
В1
22
(31)
А1
21
3 1
С1
21
15.
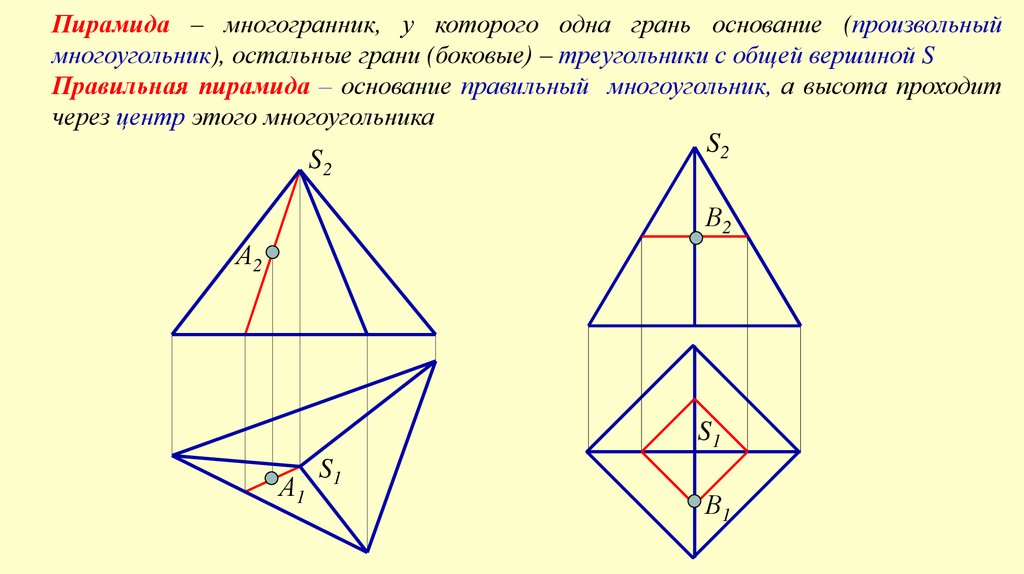
Пирамида – многогранник, у которого одна грань основание (произвольныймногоугольник), остальные грани (боковые) – треугольники с общей вершиной S
Правильная пирамида – основание правильный многоугольник, а высота проходит
через центр этого многоугольника
S2
S2
В2
А2
S1
А1
S1
В1
16.
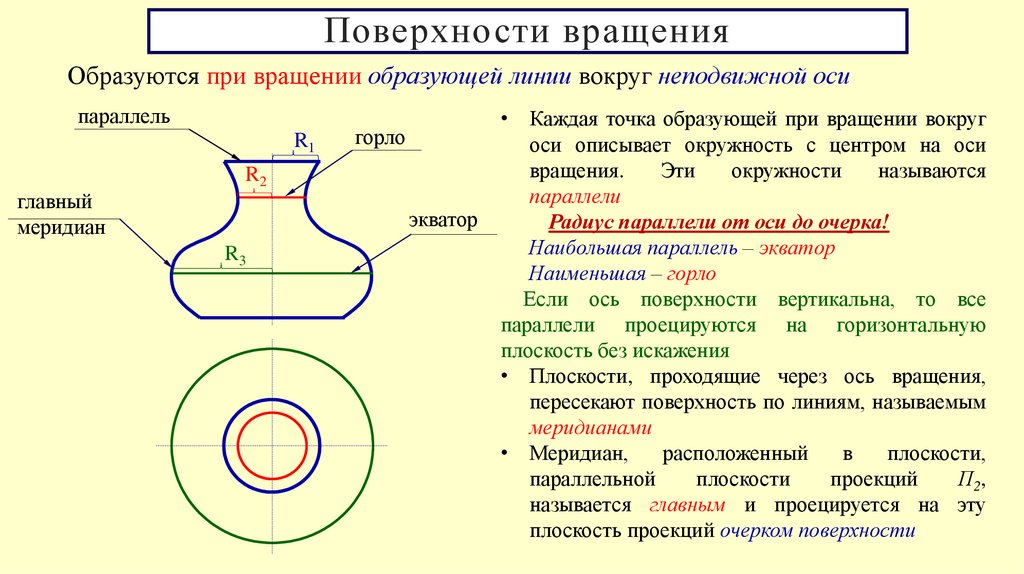
Поверхности вращенияОбразуются при вращении образующей линии вокруг неподвижной оси
параллель
R1
главный
меридиан
горло
R2
экватор
R3
• Каждая точка образующей при вращении вокруг
оси описывает окружность с центром на оси
вращения.
Эти
окружности
называются
параллели
Радиус параллели от оси до очерка!
Наибольшая параллель – экватор
Наименьшая – горло
Если ось поверхности вертикальна, то все
параллели проецируются на горизонтальную
плоскость без искажения
• Плоскости, проходящие через ось вращения,
пересекают поверхность по линиям, называемым
меридианами
• Меридиан,
расположенный
в
плоскости,
параллельной
плоскости
проекций
П2 ,
называется главным и проецируется на эту
плоскость проекций очерком поверхности
17.
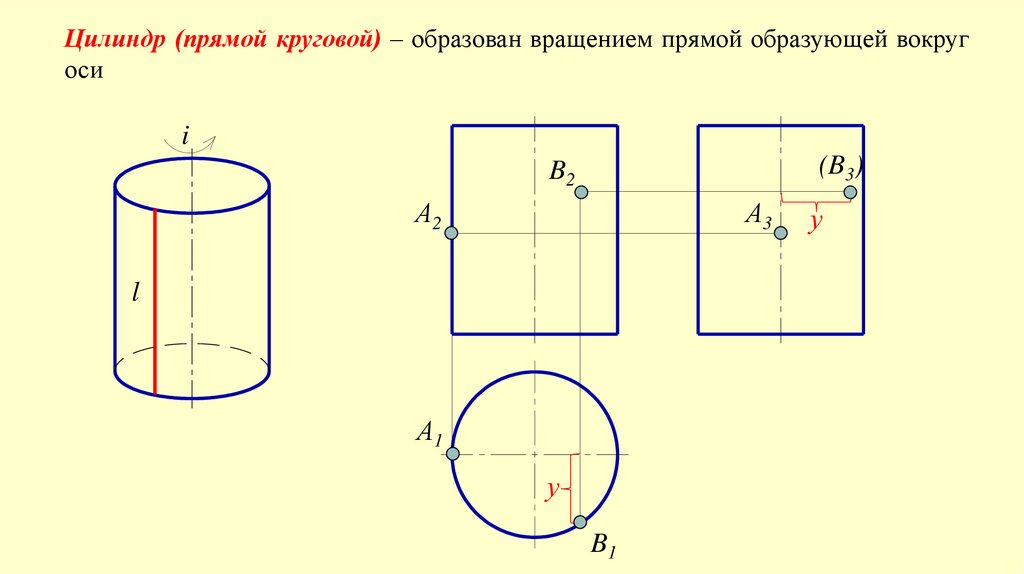
Цилиндр (прямой круговой) – образован вращением прямой образующей вокругоси
i
(B3)
B2
А3
А2
l
А1
у
B1
у
18.
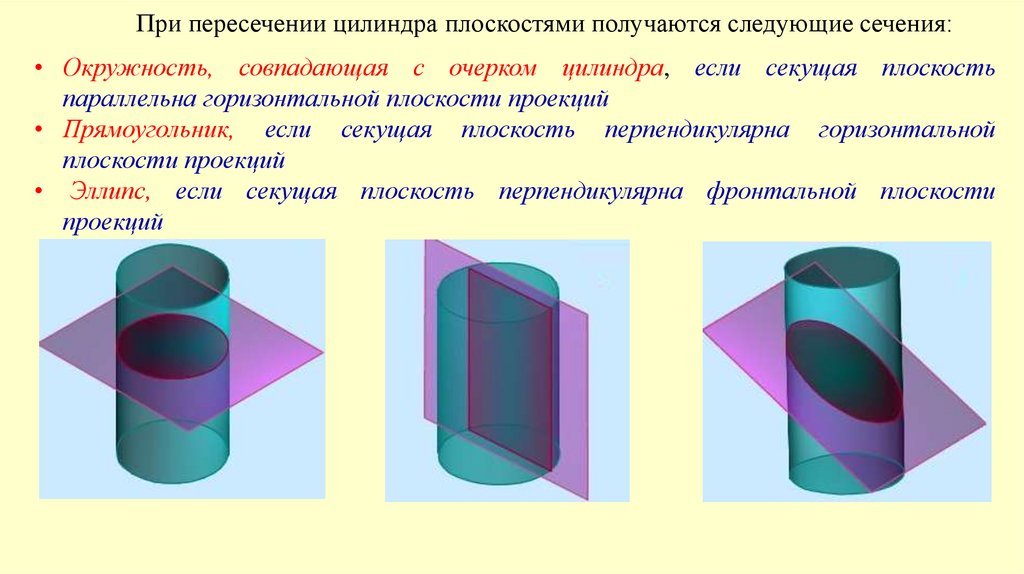
При пересечении цилиндра плоскостями получаются следующие сечения:• Окружность, совпадающая с очерком цилиндра, если секущая плоскость
параллельна горизонтальной плоскости проекций
• Прямоугольник, если секущая плоскость перпендикулярна горизонтальной
плоскости проекций
• Эллипс, если секущая плоскость перпендикулярна фронтальной плоскости
проекций
19.
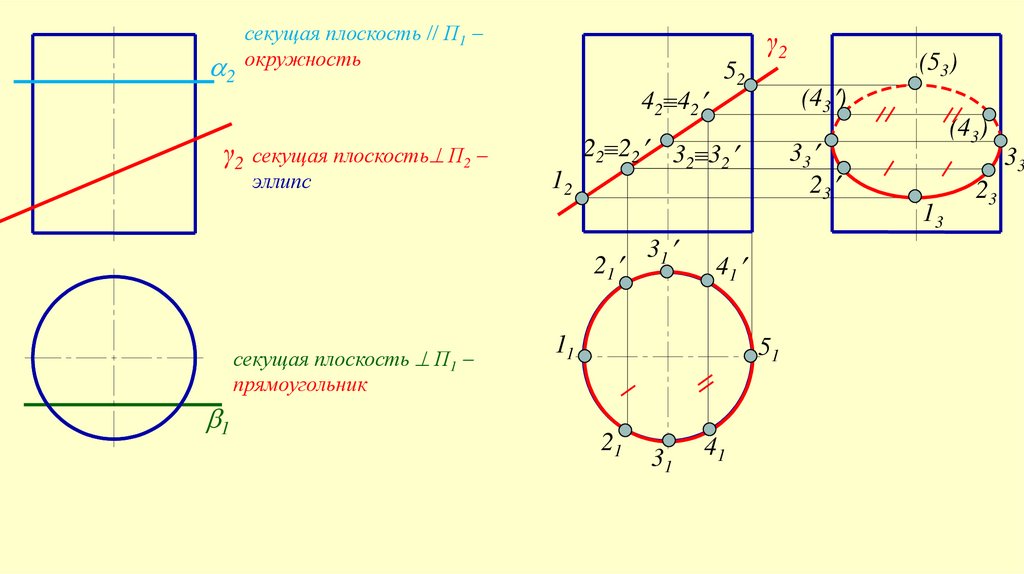
2секущая плоскость П1
окружность
42 42
γ2 секущая плоскость П2
эллипс
22 22
секущая плоскость П1
прямоугольник
1
(43 )
31
41
51
31
(43)
33
13
11
21
(53)
33
23
32 32
12
21
52
γ2
41
23
20.
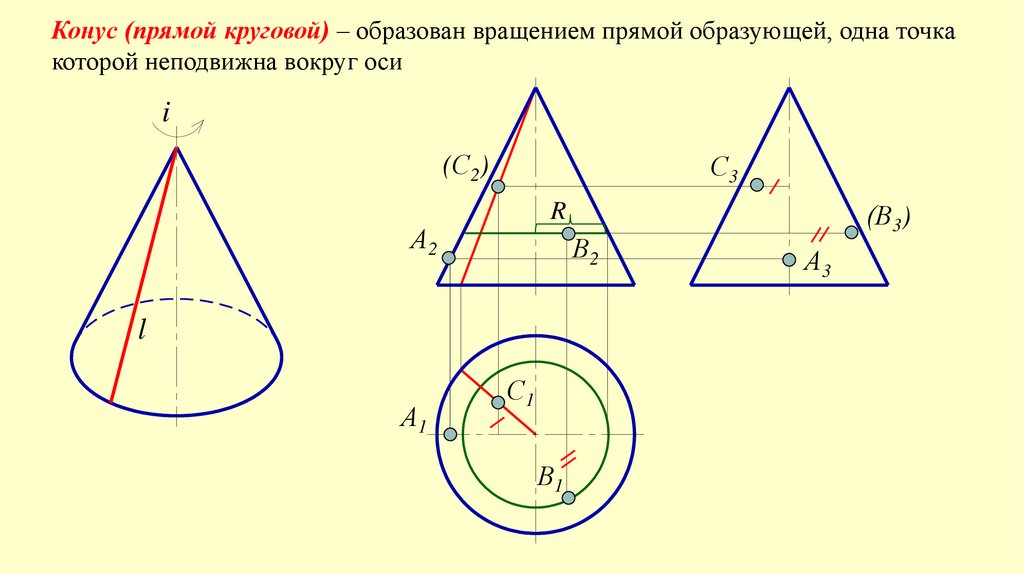
Конус (прямой круговой) – образован вращением прямой образующей, одна точкакоторой неподвижна вокруг оси
i
С3
(С2)
А2
В2
l
А1
(В3)
R
С1
В1
А3
21.
При пересечении конуса плоскостями получаются следующие сечения: плоскиекривые 2-го порядка (окружность, эллипс, парабола, гипербола), треугольник
• Треугольник, если секущая плоскость проходит через вершину конуса
• Окружность, если секущая плоскость параллельна какой- либо плоскости проекций
• Эллипс, если секущая плоскость перпендикулярна какой- либо плоскости проекций
• Парабола, если секущая плоскость параллельна какой- либо одной образующей
конуса
• Гипербола, если секущая плоскость параллельна двум образующим конуса
22.
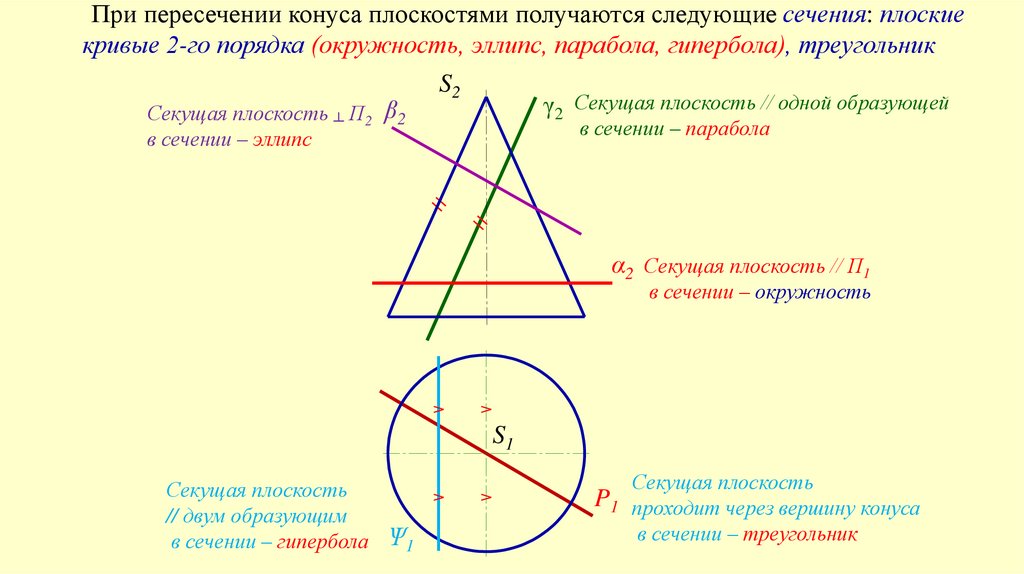
При пересечении конуса плоскостями получаются следующие сечения: плоскиекривые 2-го порядка (окружность, эллипс, парабола, гипербола), треугольник
S2
γ2 Секущая плоскость // одной образующей
Секущая плоскость ┴ П2 β2
в сечении – парабола
в сечении – эллипс
α2 Секущая плоскость // П1
в сечении – окружность
S1
Секущая плоскость
// двум образующим
в сечении – гипербола Ѱ1
Секущая плоскость
P1 проходит через вершину конуса
в сечении – треугольник
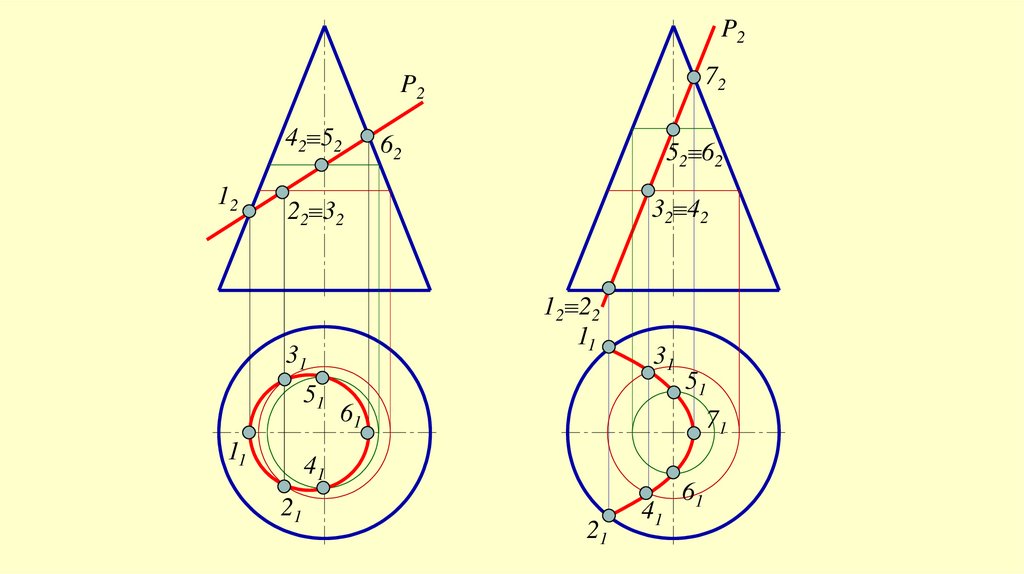
23.
P272
P2
42 52
12
52 62
62
32 42
22 32
12 22
11
31
51
11
31
61
71
41
21
51
21
41
61
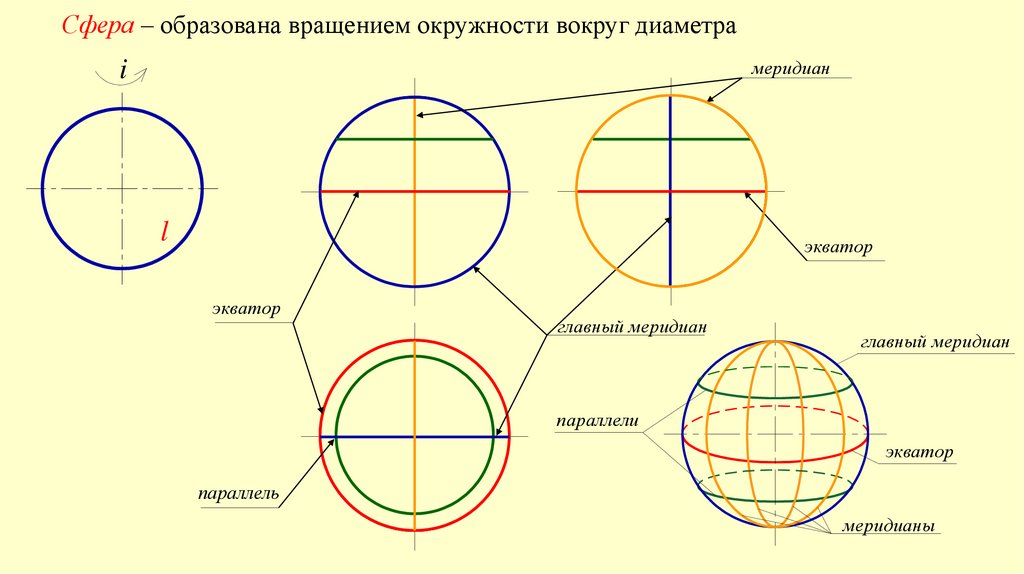
24.
Сфера – образована вращением окружности вокруг диаметрамеридиан
i
l
экватор
экватор
главный меридиан
главный меридиан
параллели
экватор
параллель
меридианы
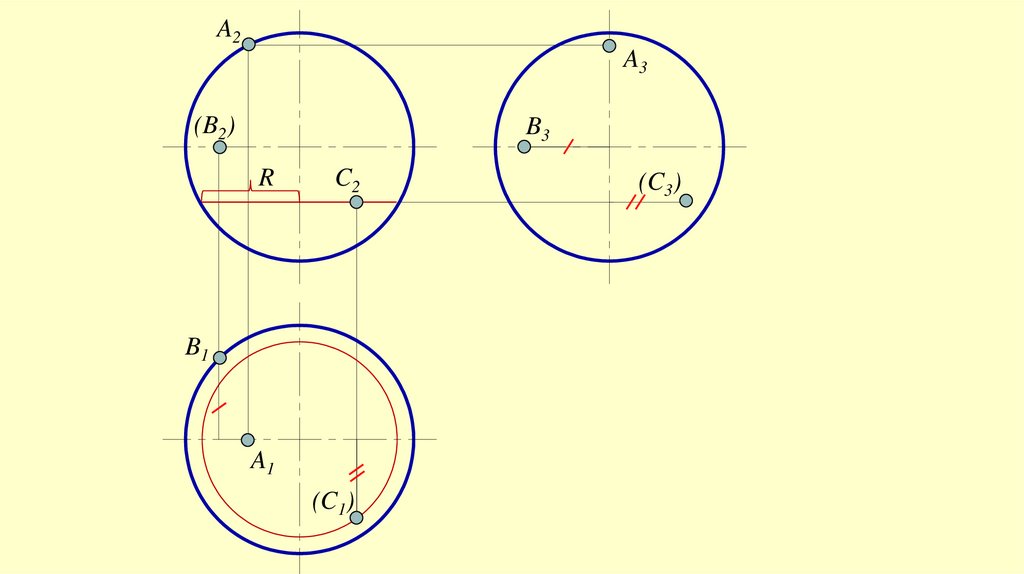
25.
A2A3
(B2)
B3
R
C2
B1
A1
(C1)
(C3)
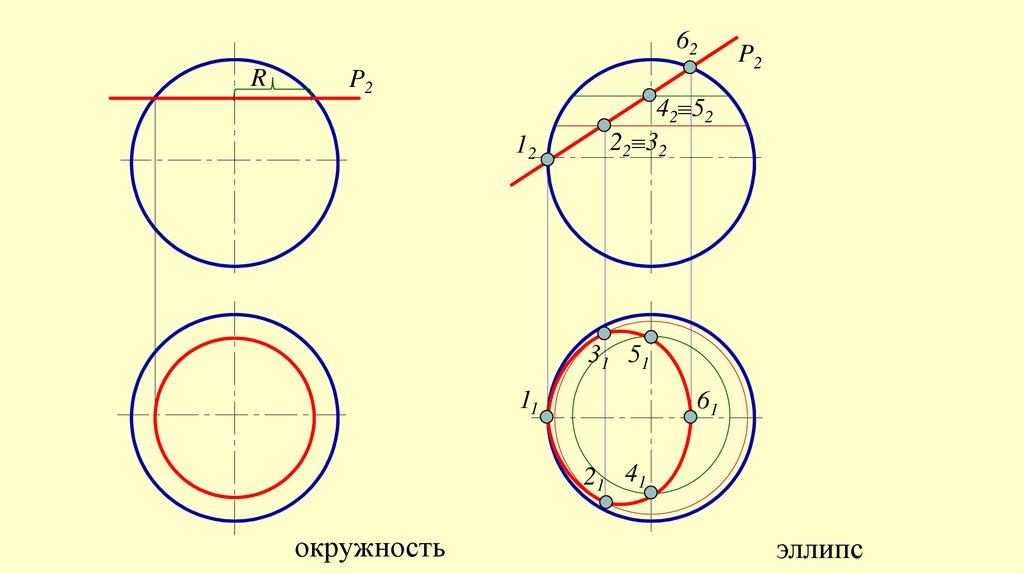
26.
При пересечении сферы плоскостями всегда получается окружность, котораяпроецируется на плоскости проекций:
В окружность, если секущая плоскость параллельна какой- либо плоскости проекций
В эллипс, если секущая плоскость перпендикулярна какой- либо плоскости проекций
27.
62R
P2
12
P2
42 52
22 32
31 51
11
61
21 41
окружность
эллипс
28.
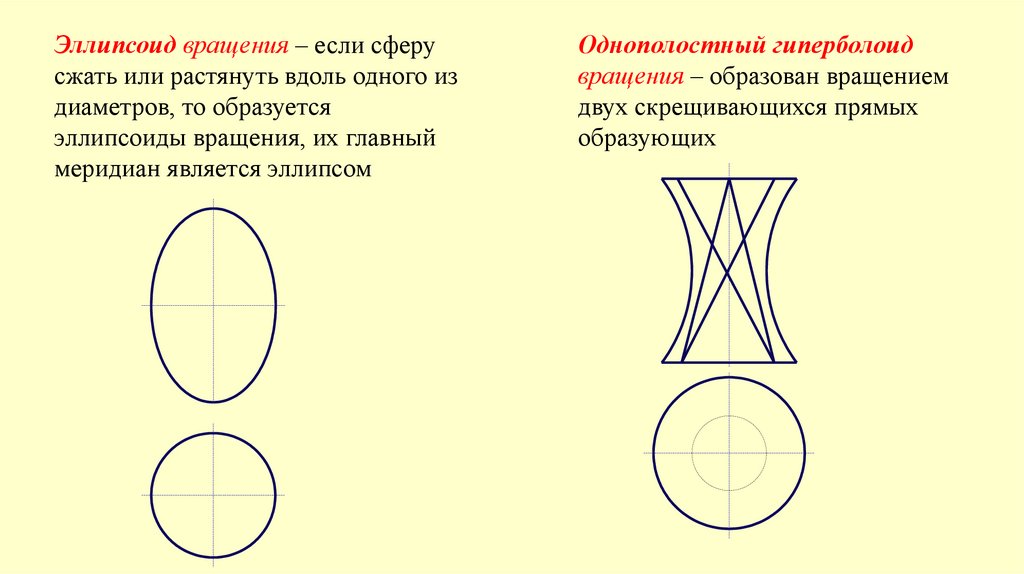
Эллипсоид вращения – если сферусжать или растянуть вдоль одного из
диаметров, то образуется
эллипсоиды вращения, их главный
меридиан является эллипсом
Однополостный гиперболоид
вращения – образован вращением
двух скрещивающихся прямых
образующих
29.
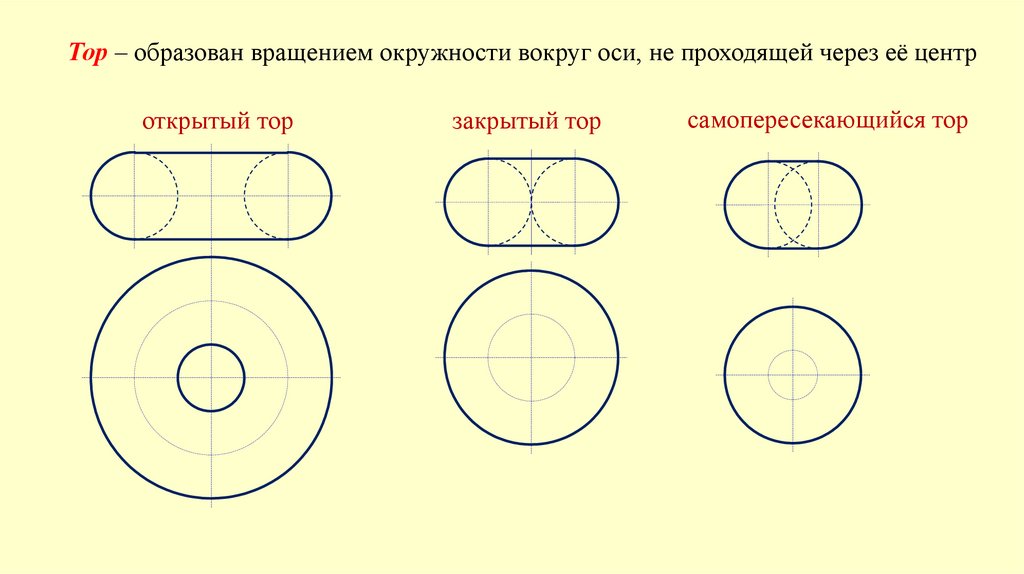
Тор – образован вращением окружности вокруг оси, не проходящей через её центроткрытый тор
закрытый тор
самопересекающийся тор
30.
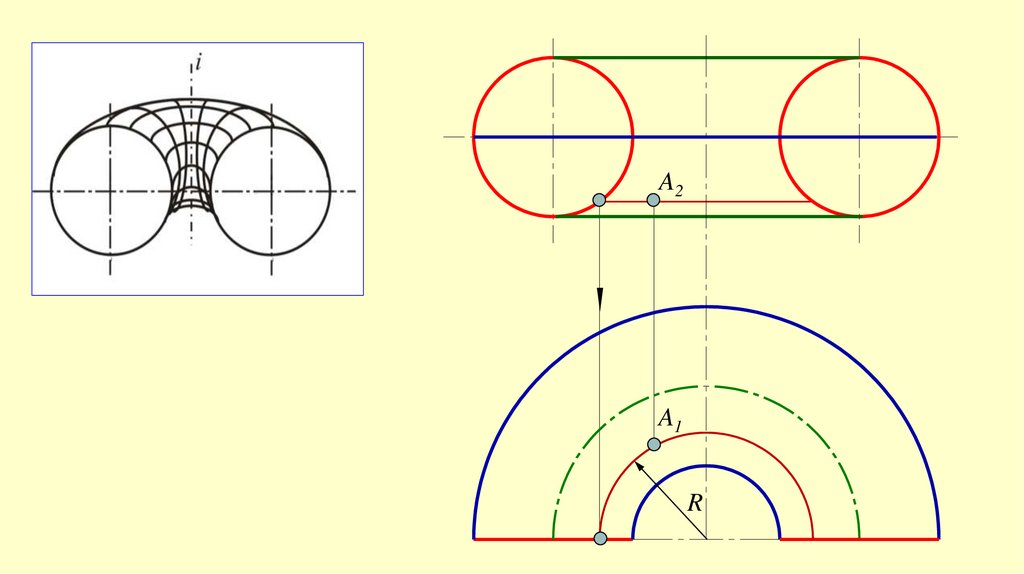
A2A1
R







 Инженерная графика
Инженерная графика








