Похожие презентации:
Кривые линии и поверхности
1.
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИ2.
КРИВЫЕ ЛИНИИ И ПОВЕРХНОСТИКривые линии
Определение: Кривую линию можно рассматривать как траекторию движущейся
точки на плоскости или в пространстве.
Кривая линия, все точки которой принадлежат плоскости, называется плоской.
Кривая линия, все точки которой не принадлежат одной плоскости, называется
пространственной или линией двоякой кривизны.
Если движение линии происходит по какому-либо закону, то поверхность
рассматривают как закономерную, в противном случае поверхность считают
незакономерной или случайной.
3.
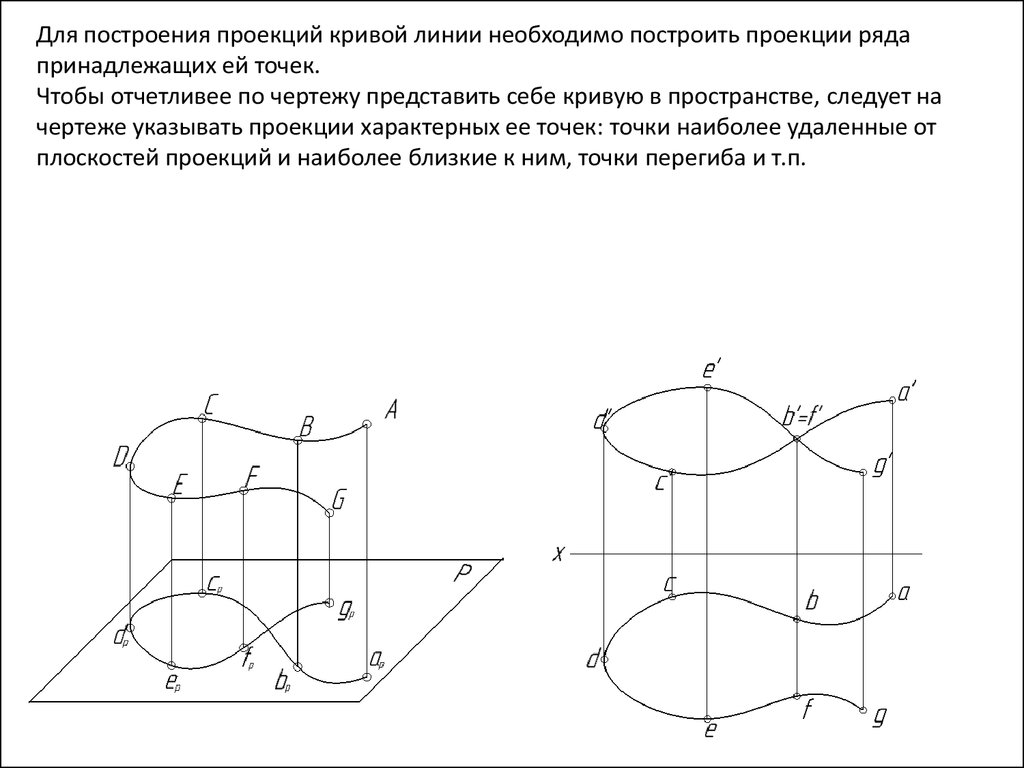
Для построения проекций кривой линии необходимо построить проекции рядапринадлежащих ей точек.
Чтобы отчетливее по чертежу представить себе кривую в пространстве, следует на
чертеже указывать проекции характерных ее точек: точки наиболее удаленные от
плоскостей проекций и наиболее близкие к ним, точки перегиба и т.п.
4.
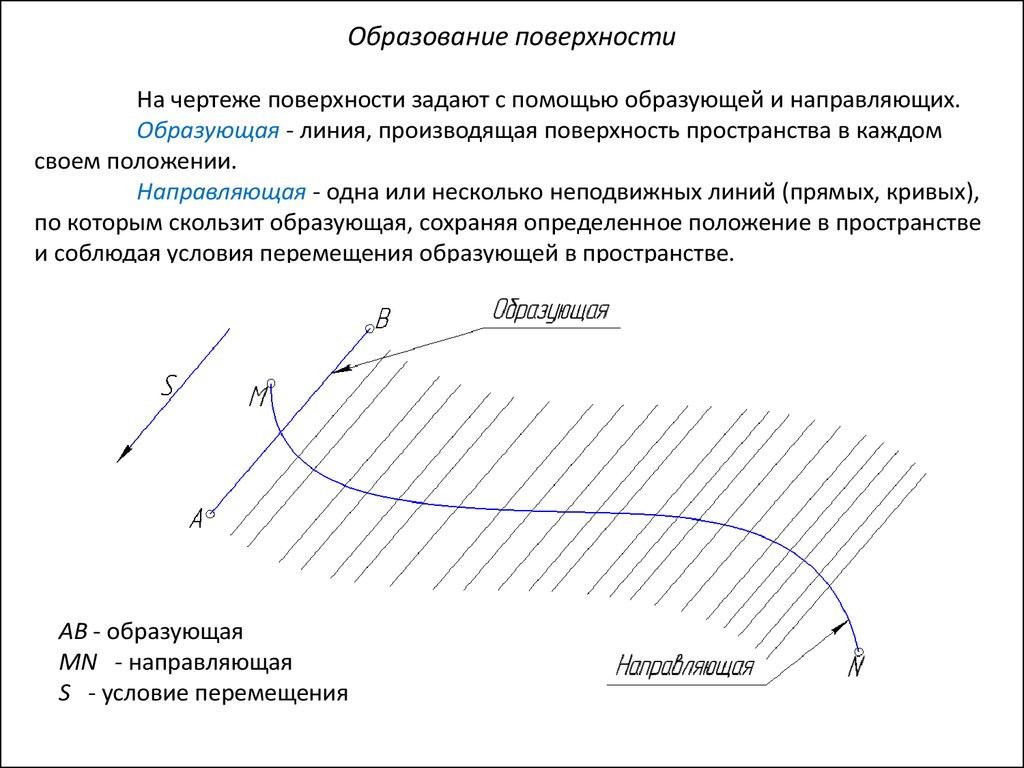
Образование поверхностиНа чертеже поверхности задают с помощью образующей и направляющих.
Образующая - линия, производящая поверхность пространства в каждом
своем положении.
Направляющая - одна или несколько неподвижных линий (прямых, кривых),
по которым скользит образующая, сохраняя определенное положение в пространстве
и соблюдая условия перемещения образующей в пространстве.
AB - образующая
MN - направляющая
S - условие перемещения
5.
Классификация поверхностейПо типу образующей:
линейчатые – образующая прямая линия (цилиндр, конус);
нелинейчатые - образующая кривая линия (сфера, тор).
По типу поверхности:
развертываемые – могут быть совмещены с плоскостью всеми своими точками без
разрывов и складок (цилиндр, конус);
неразвертываемые – в противном случае (сфера, тор).
6.
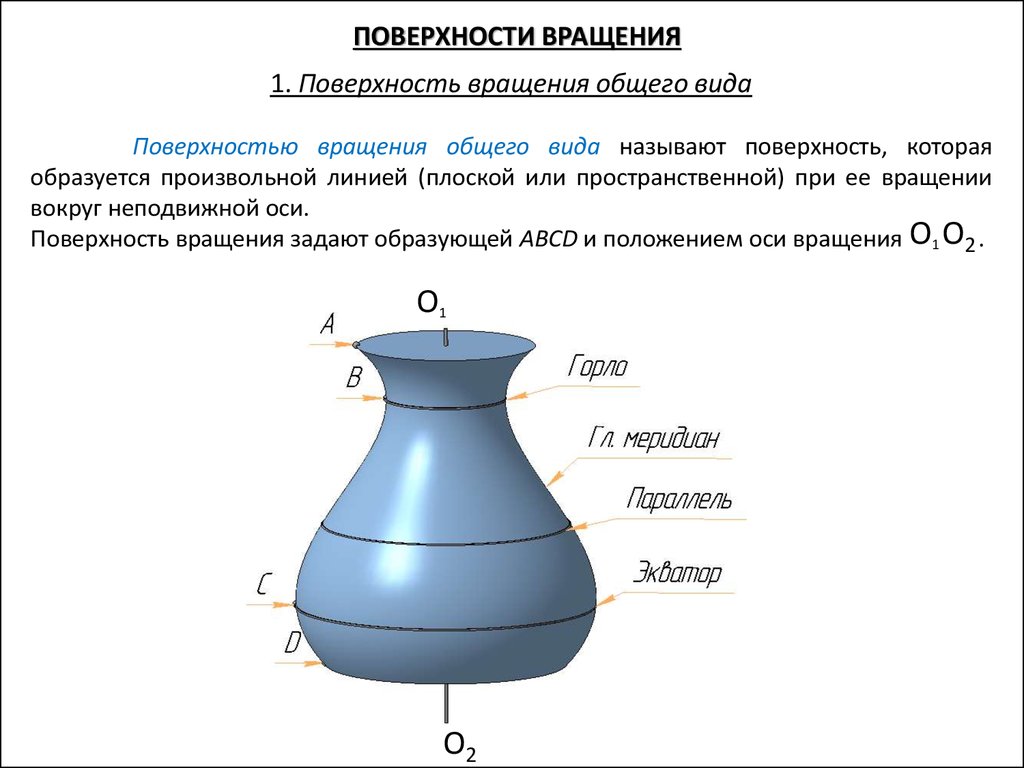
ПОВЕРХНОСТИ ВРАЩЕНИЯ1. Поверхность вращения общего вида
Поверхностью вращения общего вида называют поверхность, которая
образуется произвольной линией (плоской или пространственной) при ее вращении
вокруг неподвижной оси.
Поверхность вращения задают образующей ABCD и положением оси вращения О1 О2 .
О1
О2
7.
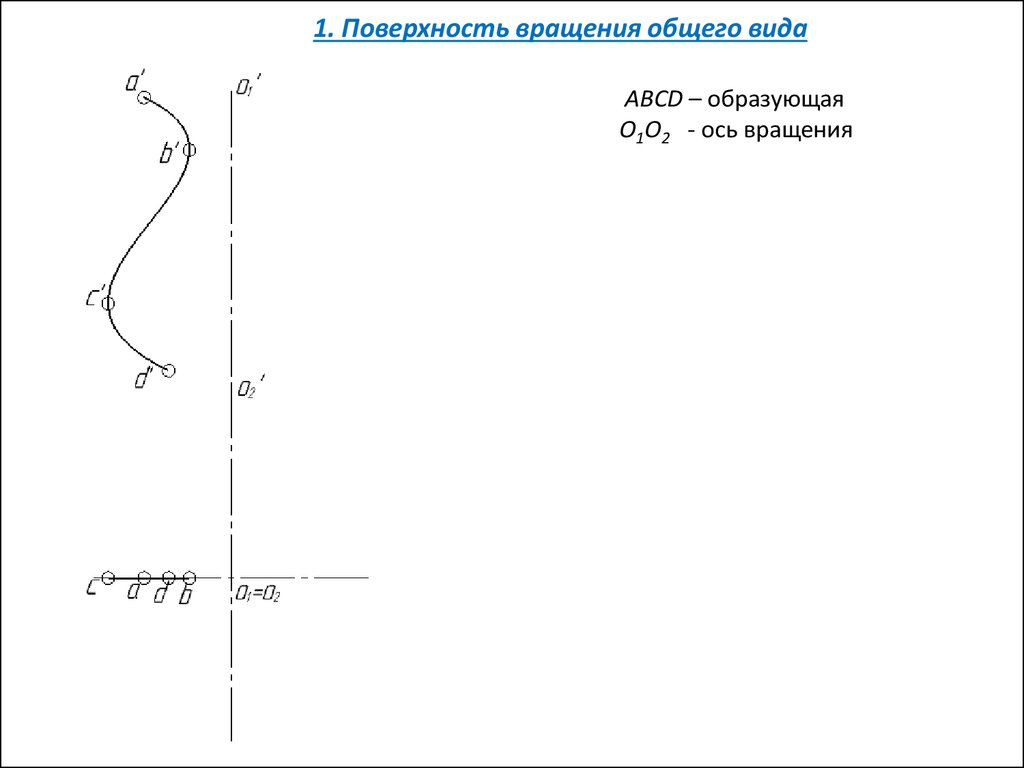
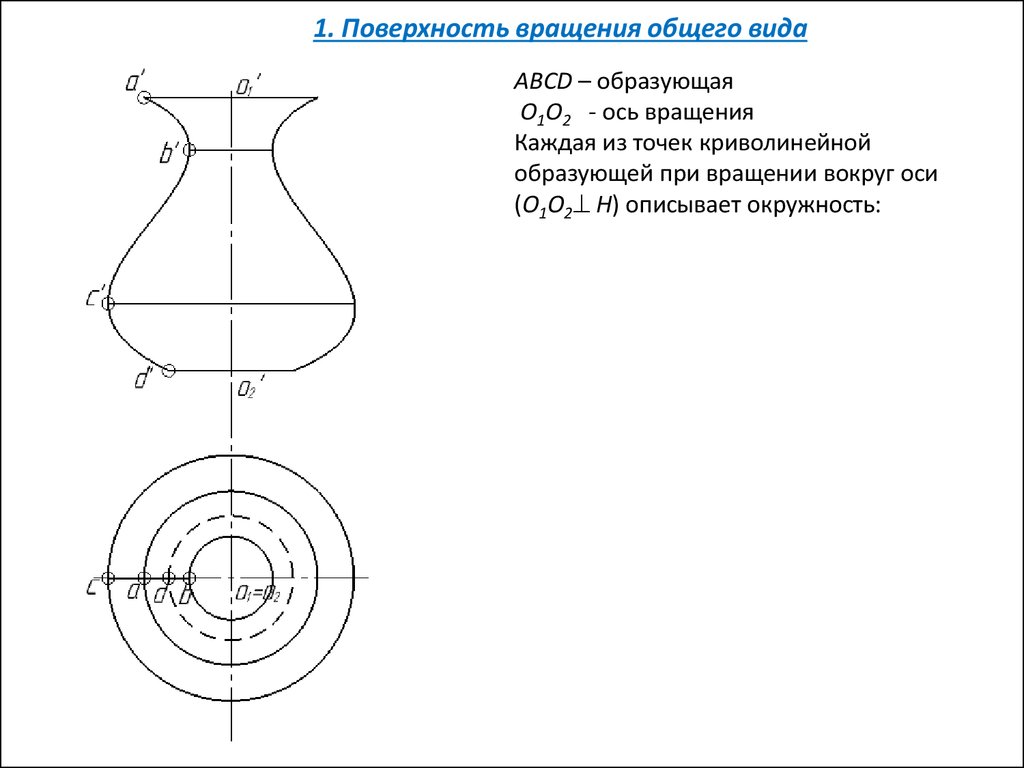
1. Поверхность вращения общего видаABCD – образующая
O1O2 - ось вращения
8.
1. Поверхность вращения общего видаABCD – образующая
O1O2 - ось вращения
Каждая из точек криволинейной
образующей при вращении вокруг оси
(O1O2 H) описывает окружность:
9.
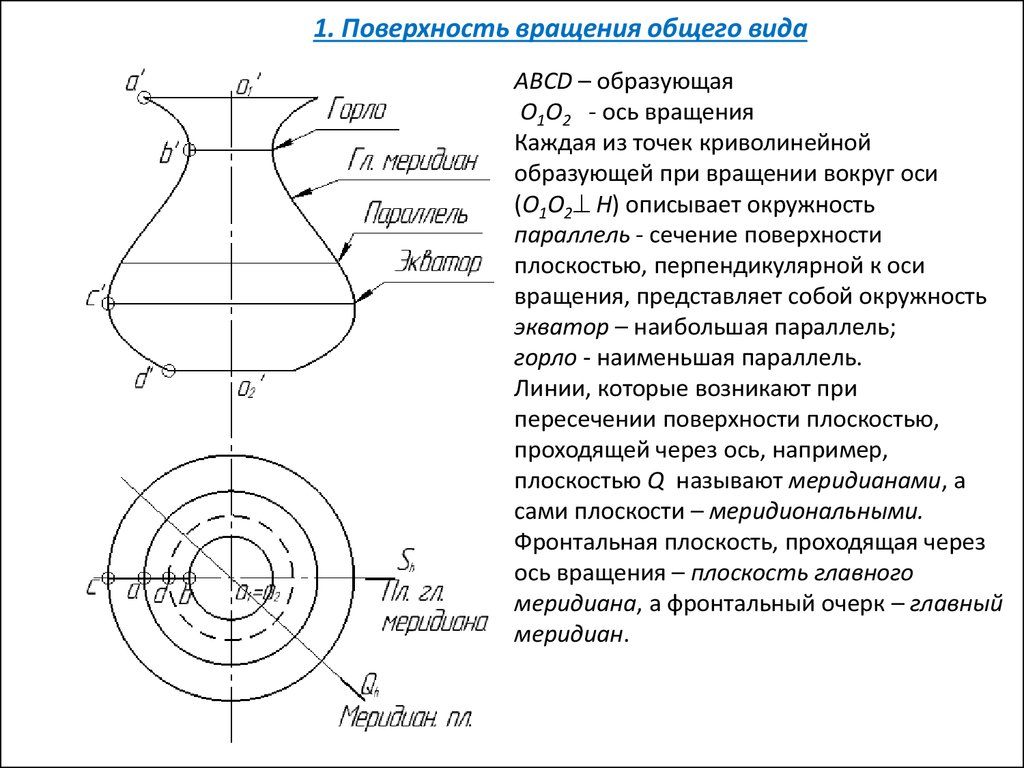
1. Поверхность вращения общего видаABCD – образующая
O1O2 - ось вращения
Каждая из точек криволинейной
образующей при вращении вокруг оси
(O1O2 H) описывает окружность
параллель - сечение поверхности
плоскостью, перпендикулярной к оси
вращения, представляет собой окружность
экватор – наибольшая параллель;
горло - наименьшая параллель.
Линии, которые возникают при
пересечении поверхности плоскостью,
проходящей через ось, например,
плоскостью Q называют меридианами, а
сами плоскости – меридиональными.
Фронтальная плоскость, проходящая через
ось вращения – плоскость главного
меридиана, а фронтальный очерк – главный
меридиан.
10.
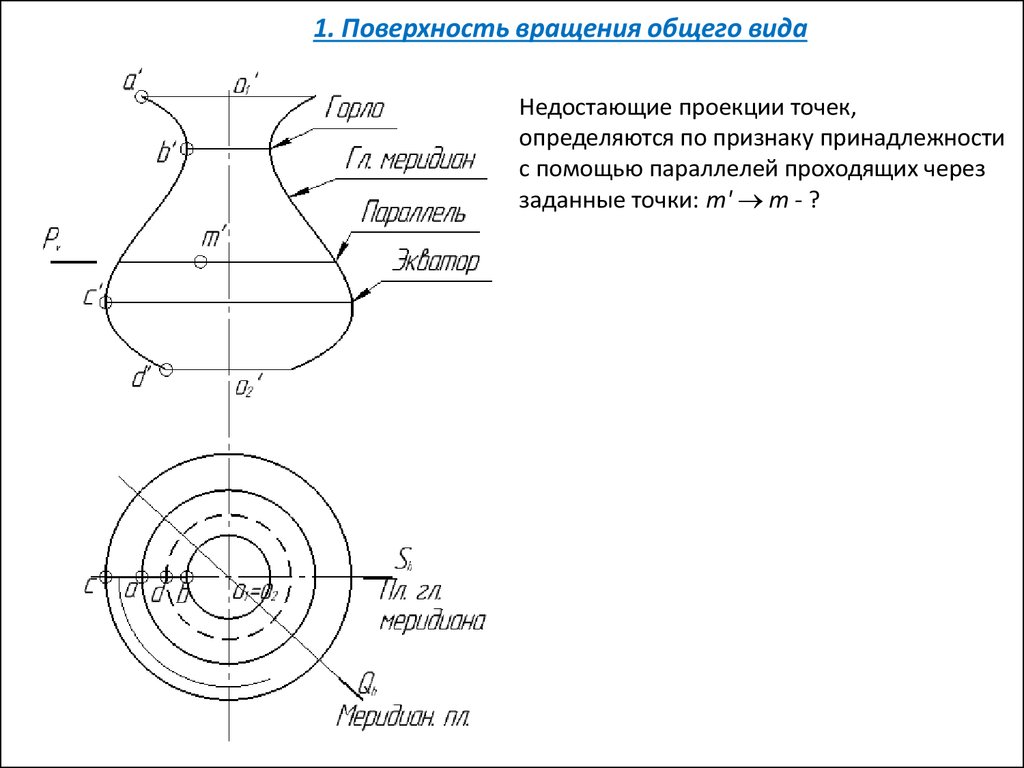
1. Поверхность вращения общего видаНедостающие проекции точек,
определяются по признаку принадлежности
с помощью параллелей проходящих через
заданные точки: m' m - ?
11.
1. Поверхность вращения общего видаНедостающие проекции точек,
определяются по признаку принадлежности
с помощью параллелей проходящих через
заданные точки: m' m - ?
12.
1. Поверхность вращения общего видаНедостающие проекции точек,
определяются по признаку принадлежности
с помощью параллелей проходящих через
заданные точки: m' m - ?
13.
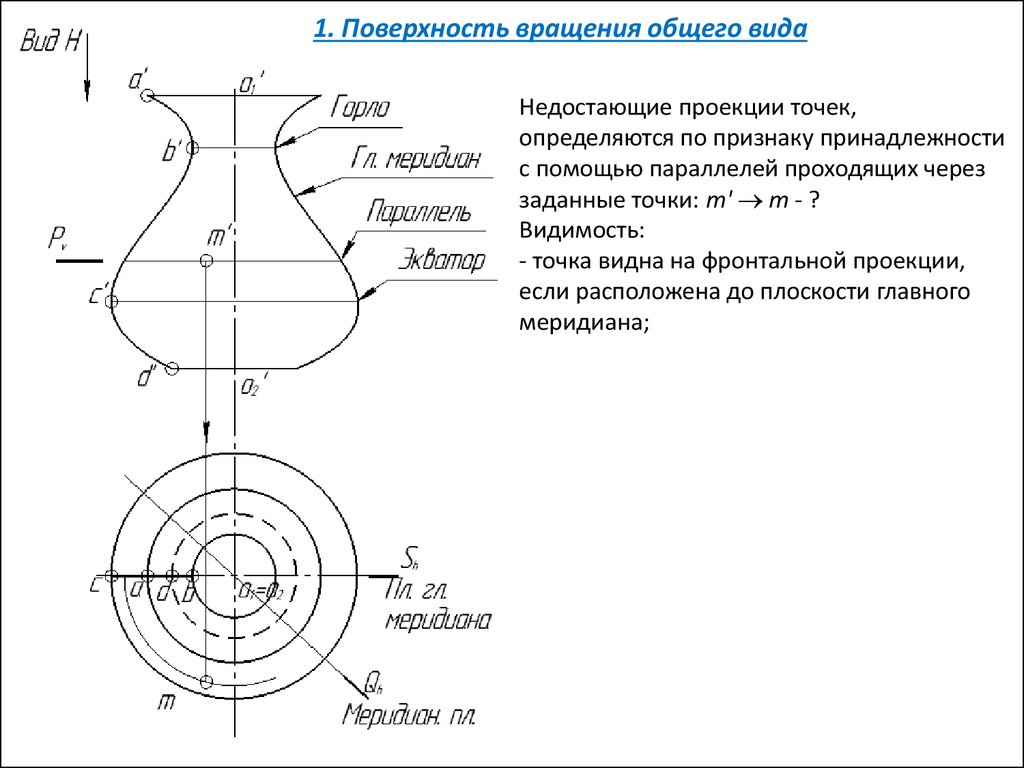
1. Поверхность вращения общего видаНедостающие проекции точек,
определяются по признаку принадлежности
с помощью параллелей проходящих через
заданные точки: m' m - ?
Видимость:
- точка видна на фронтальной проекции,
если расположена до плоскости главного
меридиана;
14.
1. Поверхность вращения общего видаНедостающие проекции точек,
определяются по признаку принадлежности
с помощью параллелей проходящих через
заданные точки: m' m - ?
Видимость:
- точка видна на фронтальной проекции,
если расположена до плоскости главного
меридиана;
- точка видна на горизонтальной проекции,
если она расположена выше экватора и
лежит на параллели, диаметр которой
больше диаметров всех параллелей,
распложенных выше точки.
15.
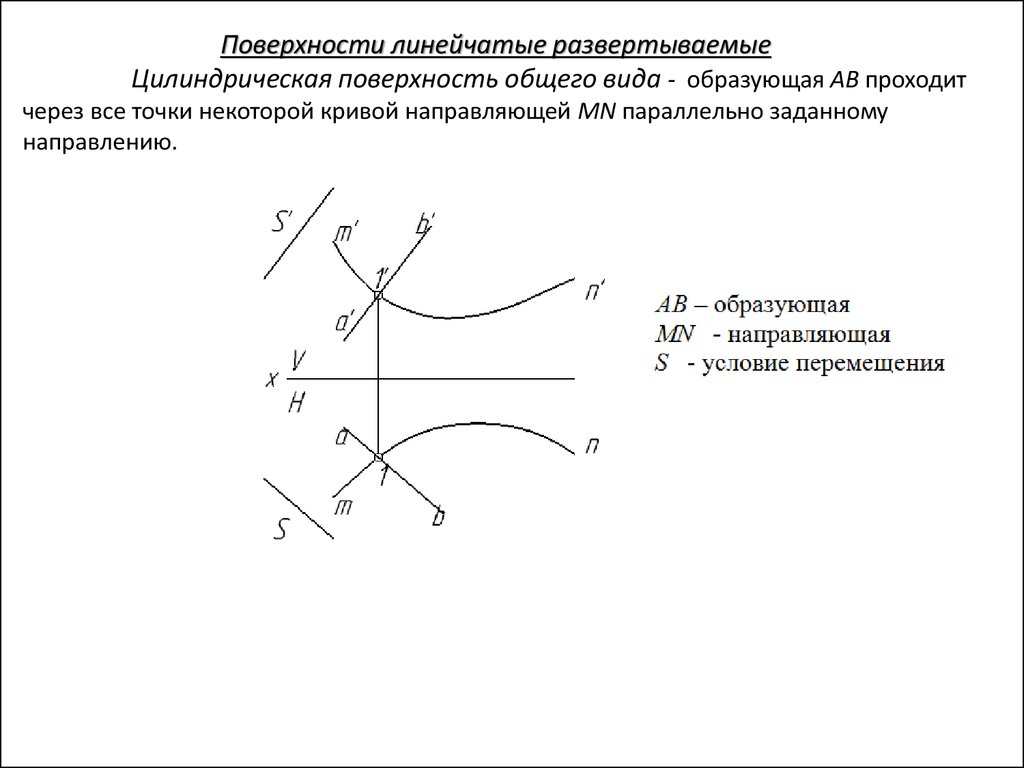
Поверхности линейчатые развертываемыеЦилиндрическая поверхность общего вида - образующая AB проходит
через все точки некоторой кривой направляющей MN параллельно заданному
направлению.
16.
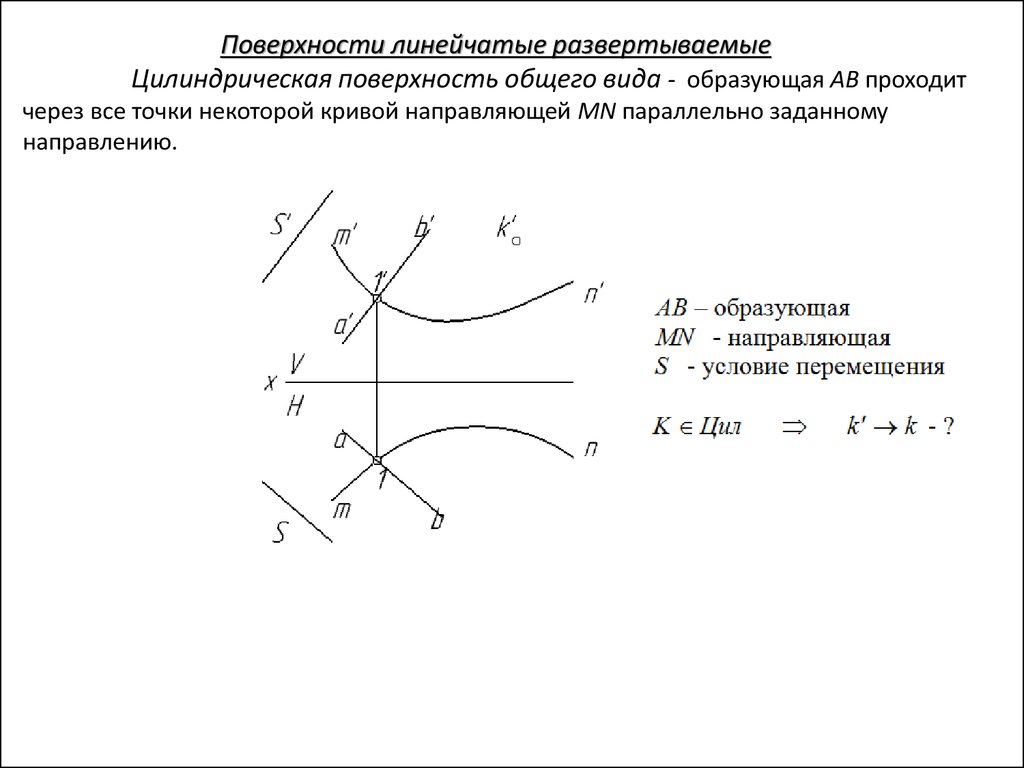
Поверхности линейчатые развертываемыеЦилиндрическая поверхность общего вида - образующая AB проходит
через все точки некоторой кривой направляющей MN параллельно заданному
направлению.
17.
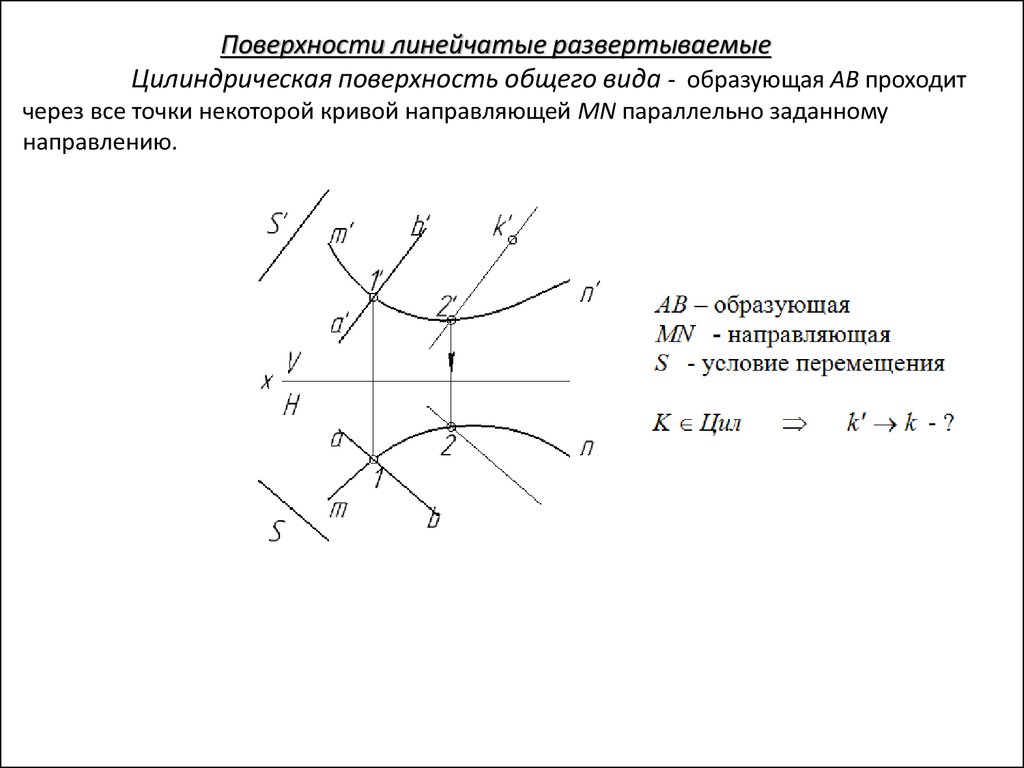
Поверхности линейчатые развертываемыеЦилиндрическая поверхность общего вида - образующая AB проходит
через все точки некоторой кривой направляющей MN параллельно заданному
направлению.
18.
Поверхности линейчатые развертываемыеЦилиндрическая поверхность общего вида - образующая AB проходит
через все точки некоторой кривой направляющей MN параллельно заданному
направлению.
19.
2. Частные виды поверхностей вращения1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая,
алгебраическая поверхность второго порядка, получается при вращении прямой
образующей вокруг оси ей параллельной.
АВ – образующая
О1О2 – ось вращения
20.
2. Частные виды поверхностей вращения1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая,
алгебраическая поверхность второго порядка, получается при вращении прямой
образующей вокруг оси ей параллельной.
АВ – образующая
О1О2 – ось вращения
21.
2. Частные виды поверхностей вращения1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая,
алгебраическая поверхность второго порядка, получается при вращении прямой
образующей вокруг оси ей параллельной.
АВ – образующая
О1О2 – ось вращения
k' k - ?
22.
2. Частные виды поверхностей вращения1). Цилиндр вращения (прямой круговой цилиндр)– линейчатая, развертываемая,
алгебраическая поверхность второго порядка, получается при вращении прямой
образующей вокруг оси ей параллельной.
АВ – образующая
О1О2 – ось вращения
k' k - ?
23.
Коническая поверхность общего вида - образующая SA проходит черезнекоторую неподвижную точку S (вершину) и последовательно через все точки
некоторой кривой направляющей MN.
SA - образующая
MN – направляющая
24.
Коническая поверхность общего вида - образующая SA проходит черезнекоторую неподвижную точку S (вершину) и последовательно через все точки
некоторой кривой направляющей MN.
SA - образующая
MN – направляющая
K Кон k' k - ?
25.
Коническая поверхность общего вида - образующая SA проходит черезнекоторую неподвижную точку S (вершину) и последовательно через все точки
некоторой кривой направляющей MN.
SA - образующая
MN – направляющая
K Кон k' k - ?
K S2 k' s’2’; k s2
26.
Коническая поверхность общего вида - образующая SA проходит черезнекоторую неподвижную точку S (вершину) и последовательно через все точки
некоторой кривой направляющей MN.
SA - образующая
MN – направляющая
K Кон k' k - ?
K S2 k' s’2’; k s2
27.
Коническая поверхность общего вида - образующая SA проходит черезнекоторую неподвижную точку S (вершину) и последовательно через все точки
некоторой кривой направляющей MN.
SA - образующая
MN – направляющая
K Кон k' k - ?
K S2 k' s’2’; k s2
28.
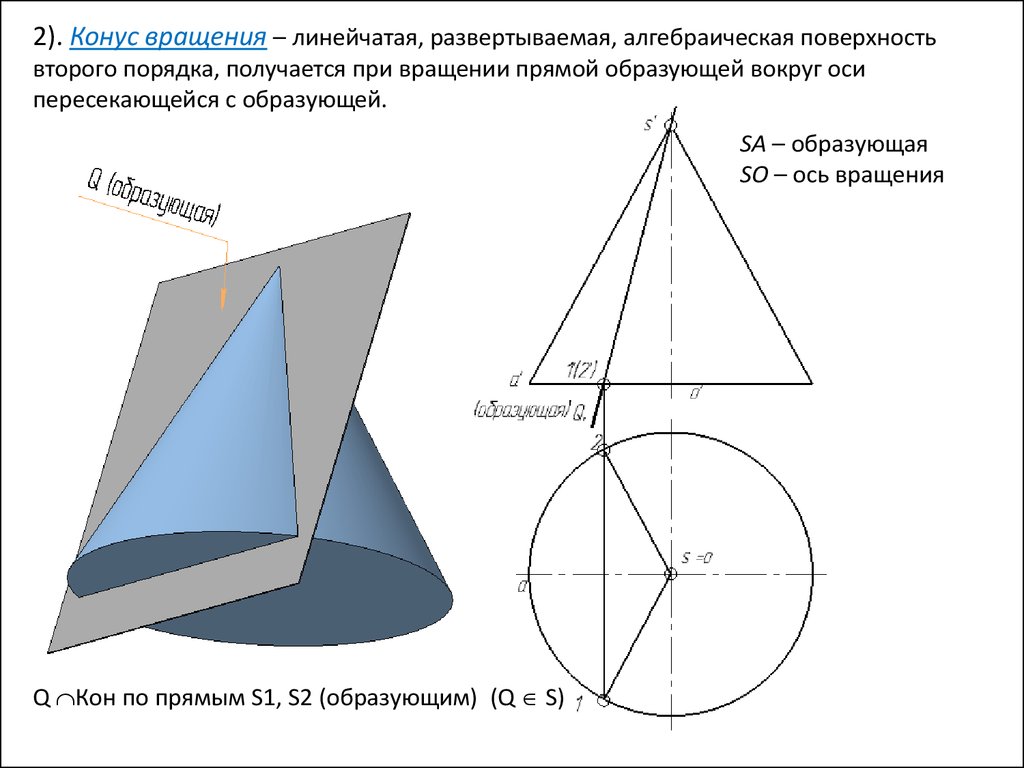
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
SА – образующая
SO – ось вращения
Q Кон по прямым S1, S2 (образующим) (Q S)
29.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
SА – образующая
SO – ось вращения
Q Кон по прямым S1, S2 (образующим) (Q S)
30.
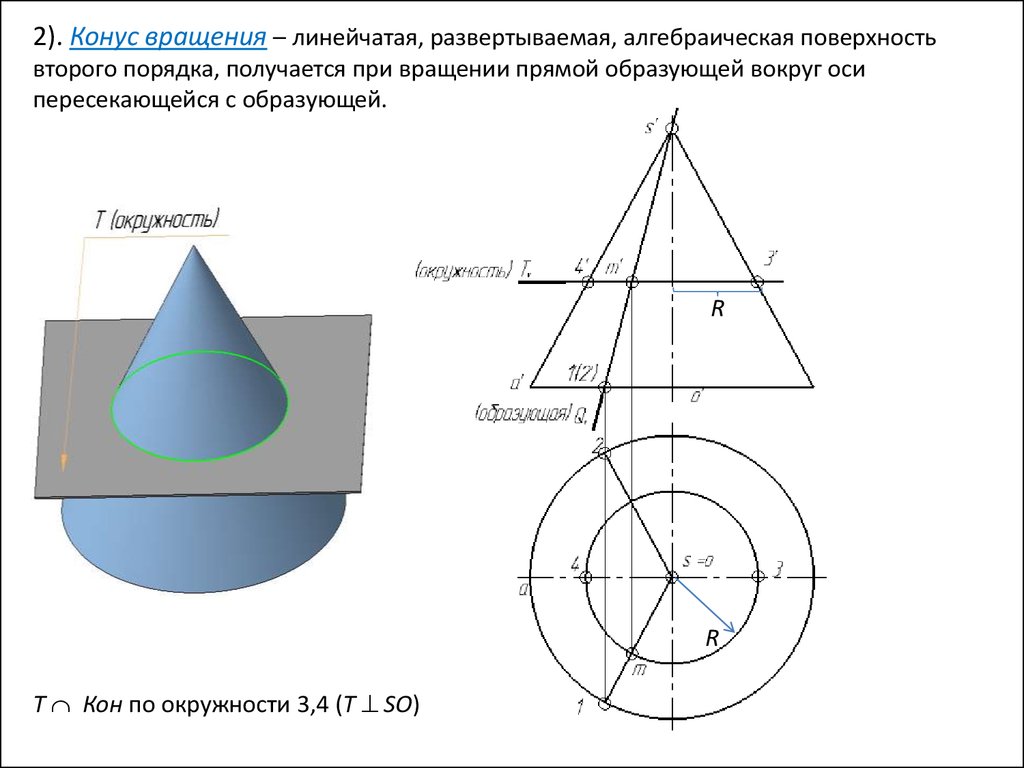
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
Т Кон по окружности 3,4 (T SO)
31.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
R
R
Т Кон по окружности 3,4 (T SO)
32.
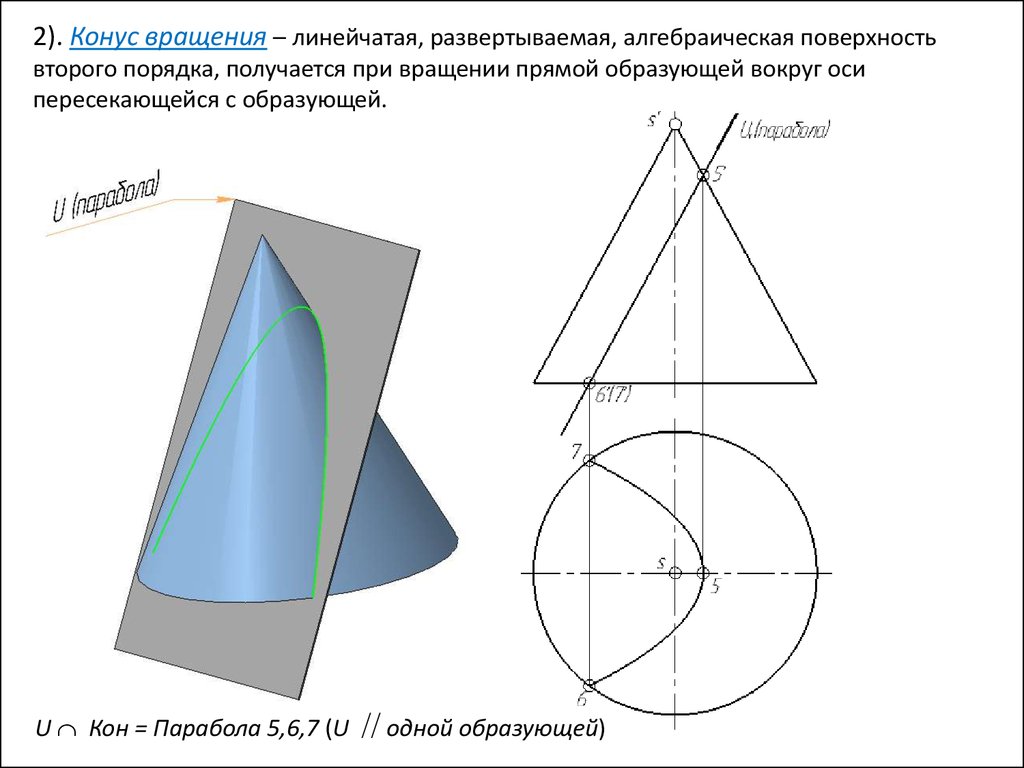
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
U Кон = Парабола 5,6,7 (U одной образующей)
33.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
U Кон = Парабола 5,6,7 (U одной образующей)
34.
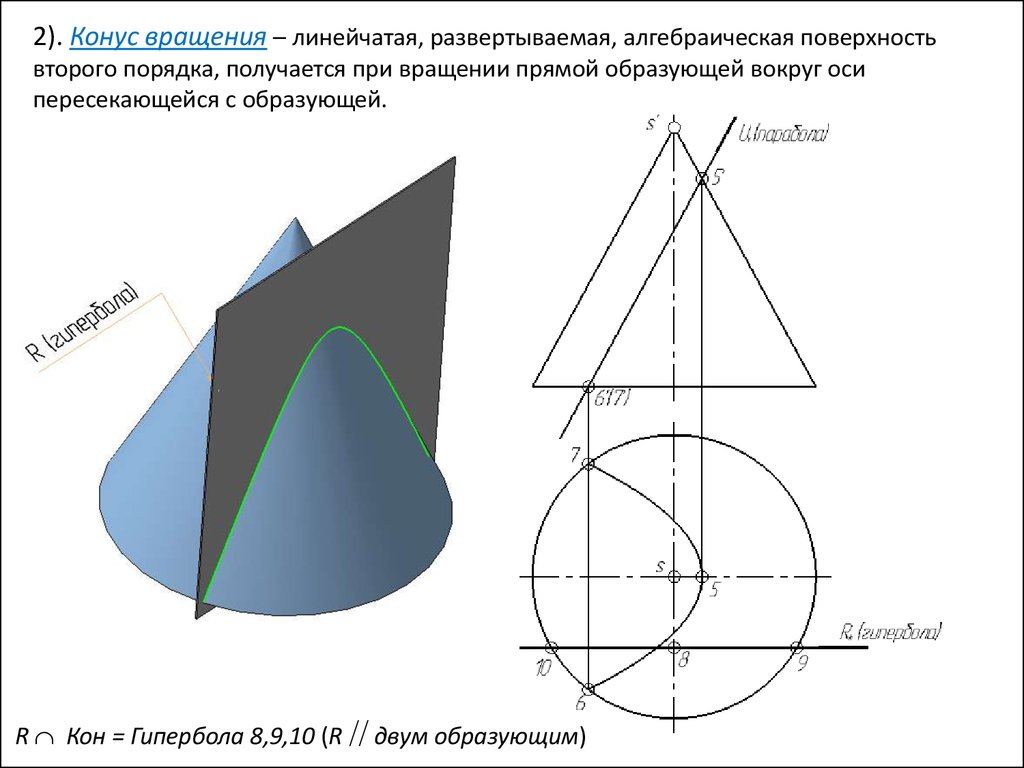
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
R Кон = Гипербола 8,9,10 (R двум образующим)
35.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
R Кон = Гипербола 8,9,10 (R двум образующим)
36.
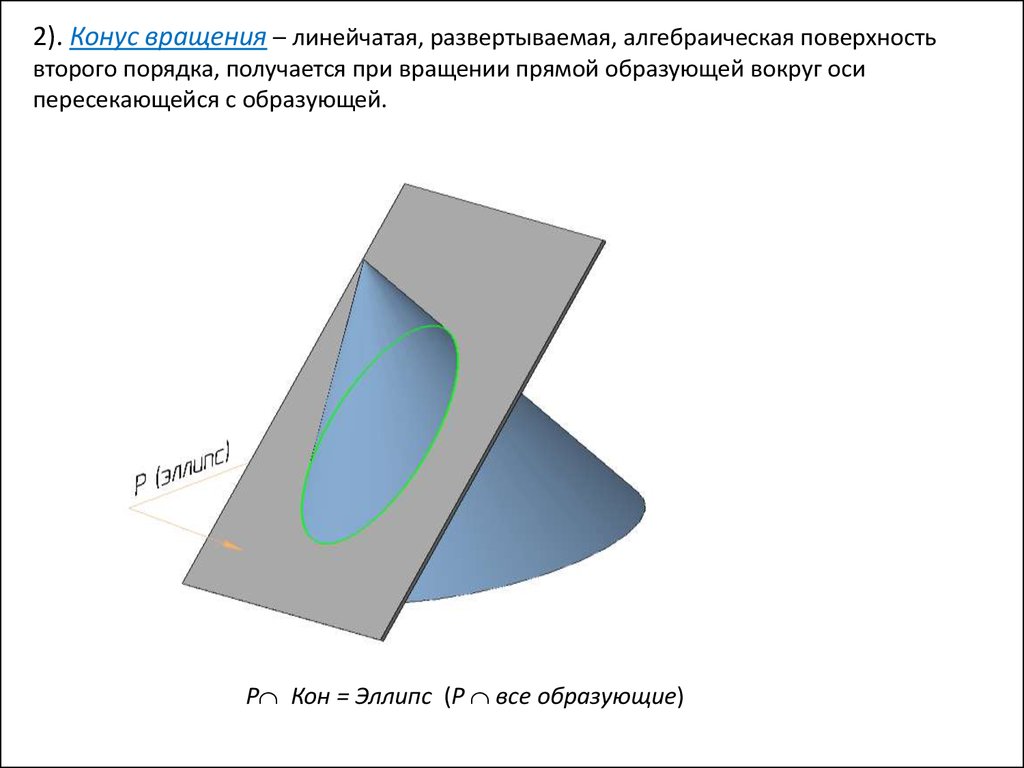
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
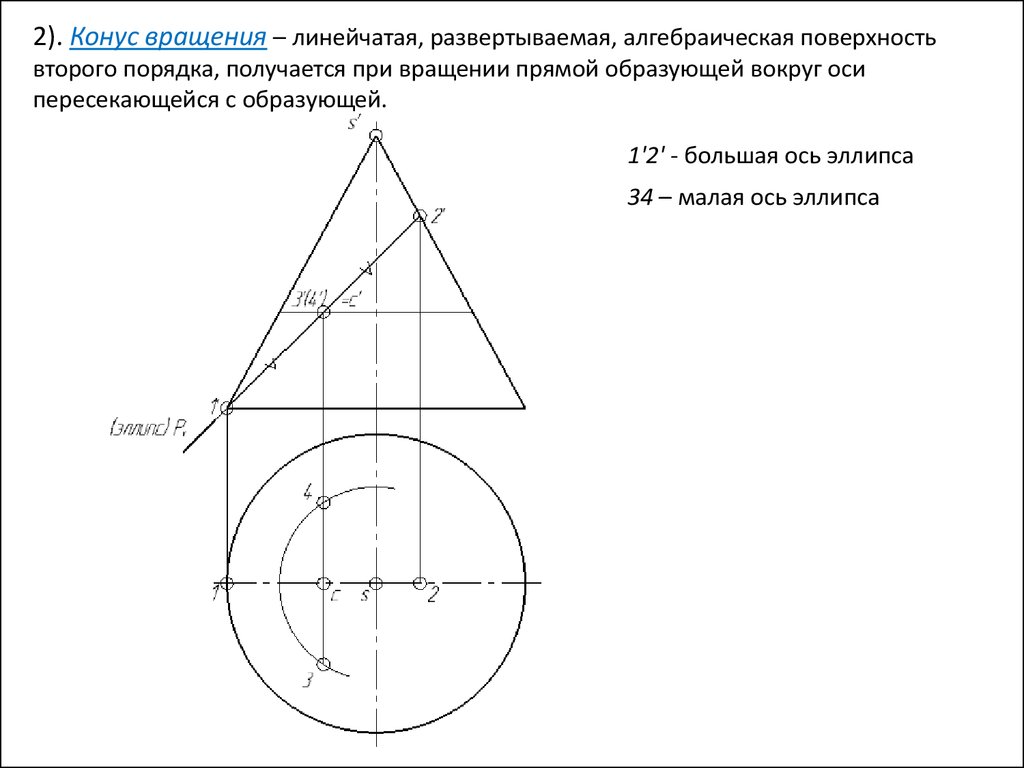
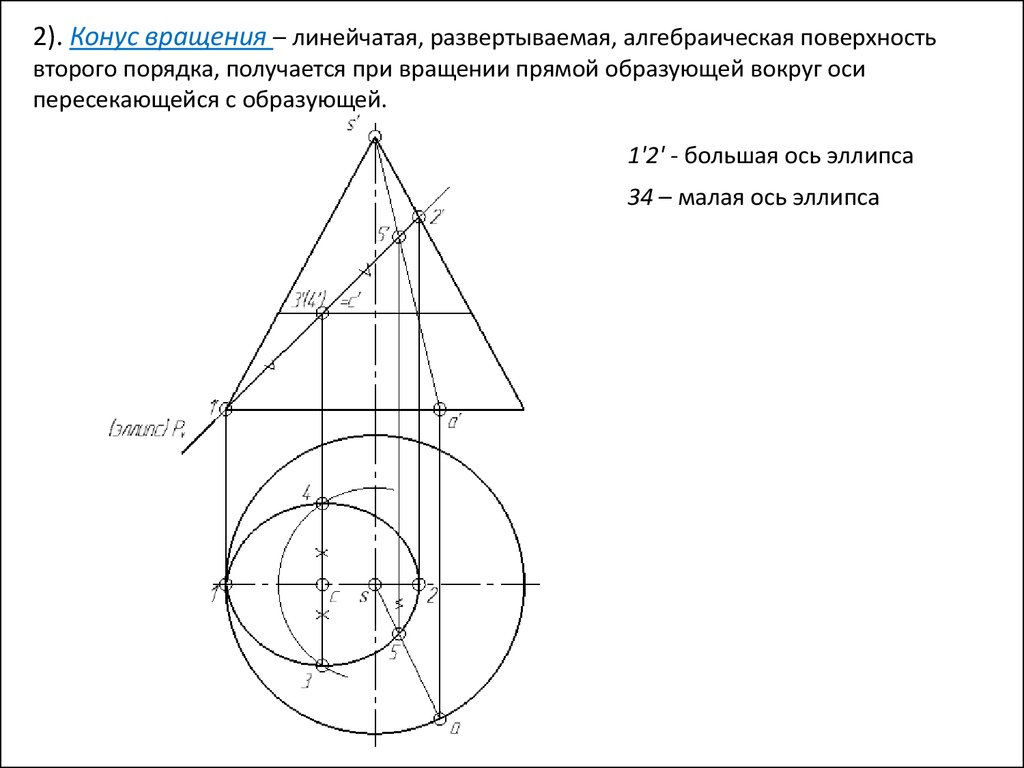
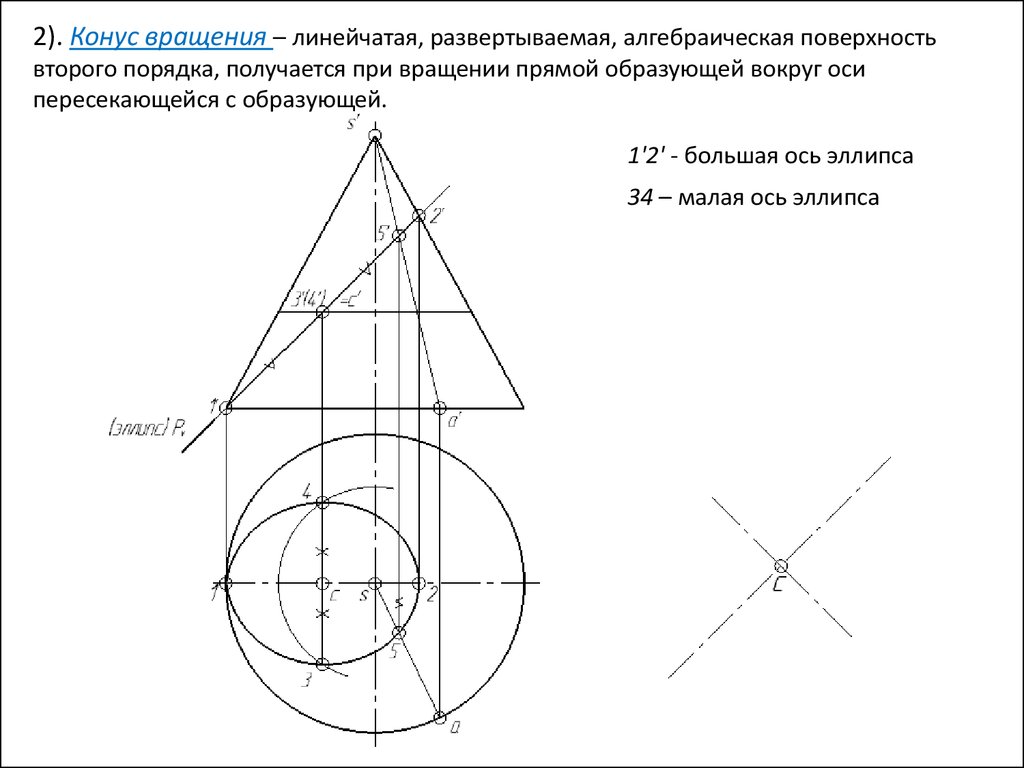
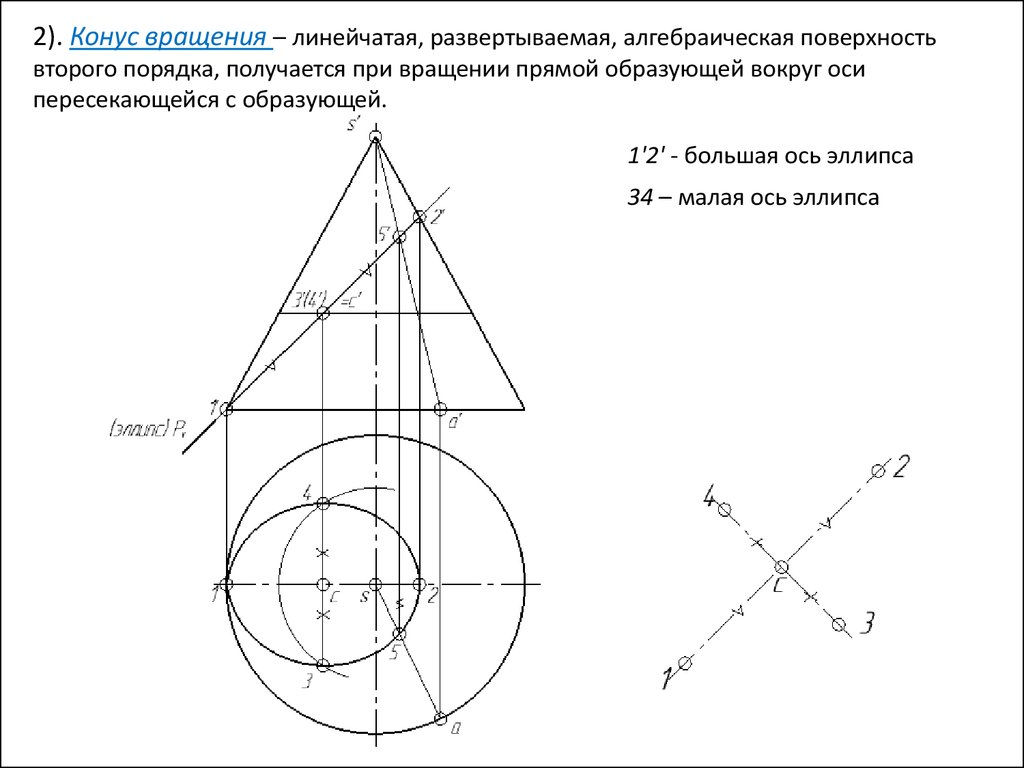
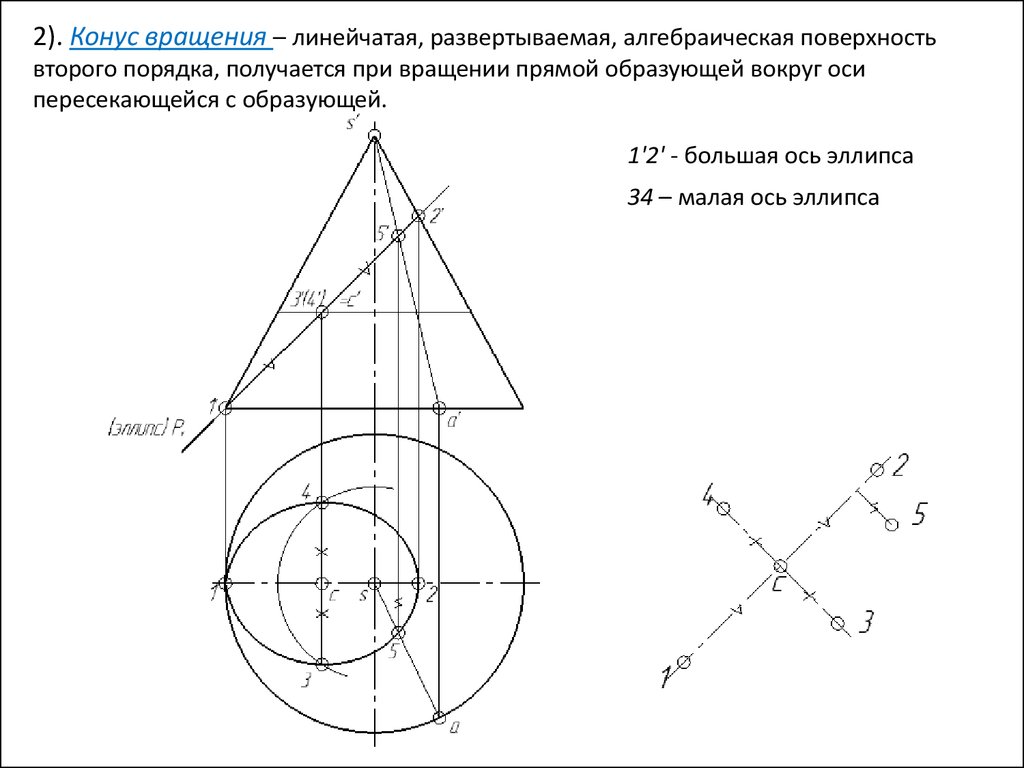
Р Кон = Эллипс (P все образующие)
37.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.v
1'2' - большая ось эллипса
38.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
39.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
40.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
41.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
42.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
43.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
44.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
45.
2). Конус вращения – линейчатая, развертываемая, алгебраическая поверхностьвторого порядка, получается при вращении прямой образующей вокруг оси
пересекающейся с образующей.
1'2' - большая ось эллипса
34 – малая ось эллипса
46.
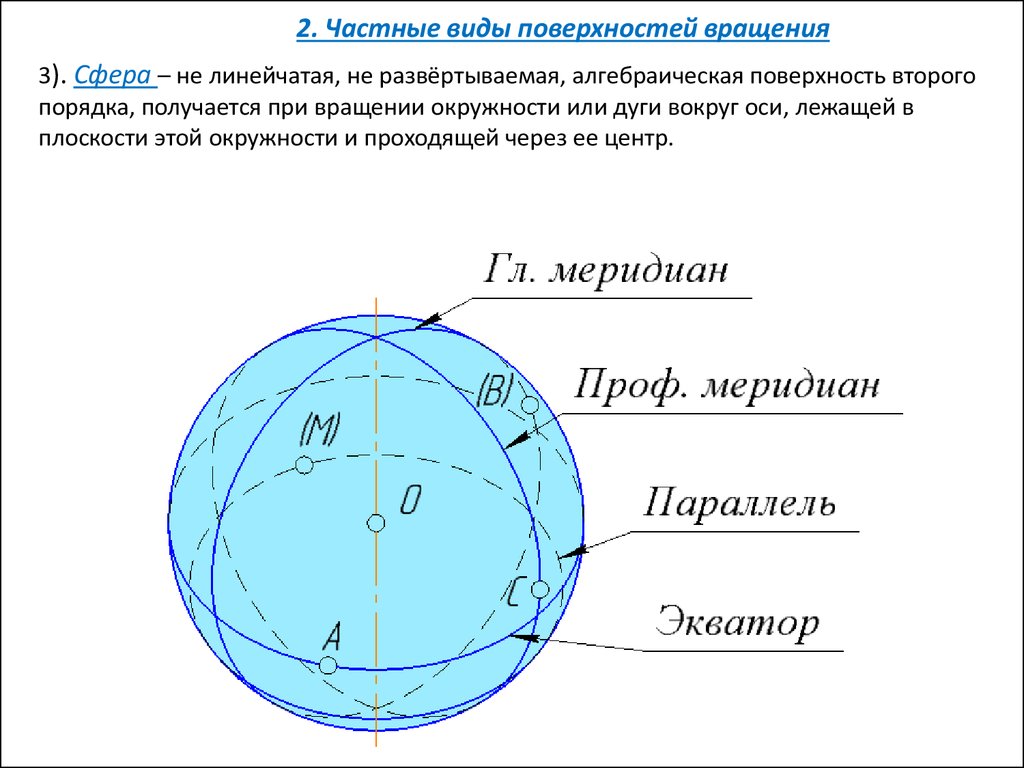
2. Частные виды поверхностей вращения3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго
порядка, получается при вращении окружности или дуги вокруг оси, лежащей в
плоскости этой окружности и проходящей через ее центр.
47.
2. Частные виды поверхностей вращения3). Сфера – не линейчатая, не развёртываемая, алгебраическая поверхность второго
порядка, получается при вращении окружности или дуги вокруг оси, лежащей в
плоскости этой окружности и проходящей через ее центр.
48.
Очерк сферы на любую ПП – окружность:- на плоскости Н – экватор;
- на плоскости V - главный меридиан;
- на плоскости W - профильный меридиан.
Окружности параллельные экватору –
параллели.
49.
Видимость сферической поверхности на плоскости Н определяет экватор:точки выше экватора – видны, ниже – не видны.
Видимость сферической поверхности на плоскости V определяет главный меридиан,
на плоскости W – профильный меридиан.
50.
a a', a ?Точка А принадлежит экватору на горизонтальной ПП и проекциям экватора на
фронтальной и профильной ПП.
Профильная проекция т. А определяется координатным методом по координате YA.
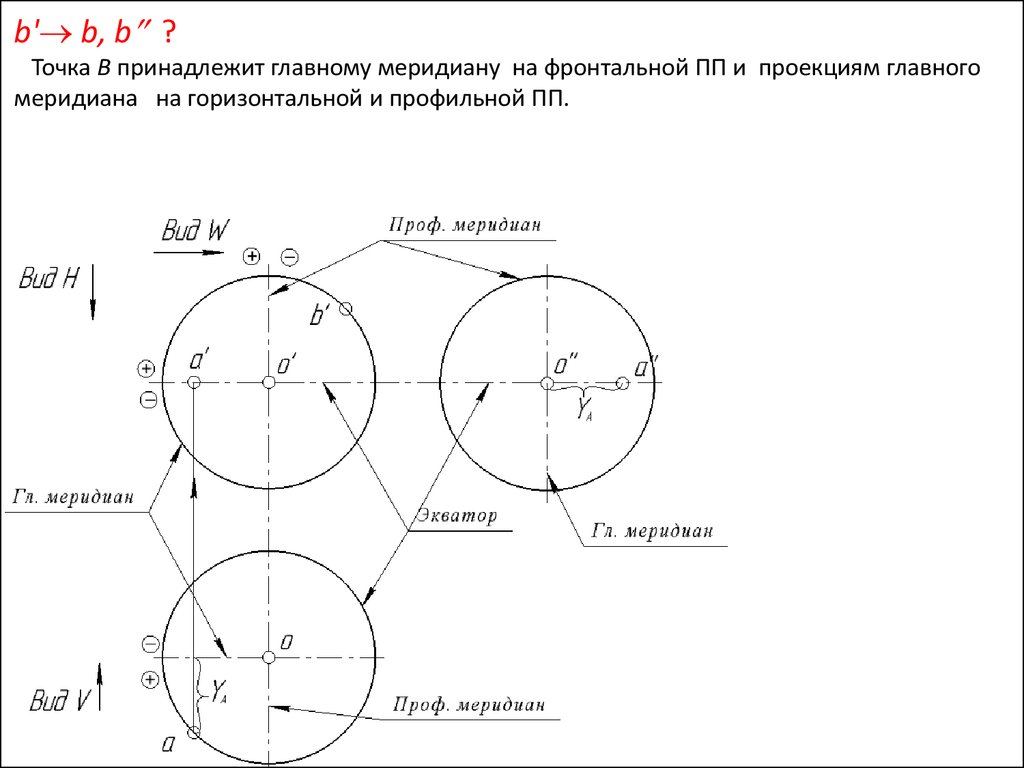
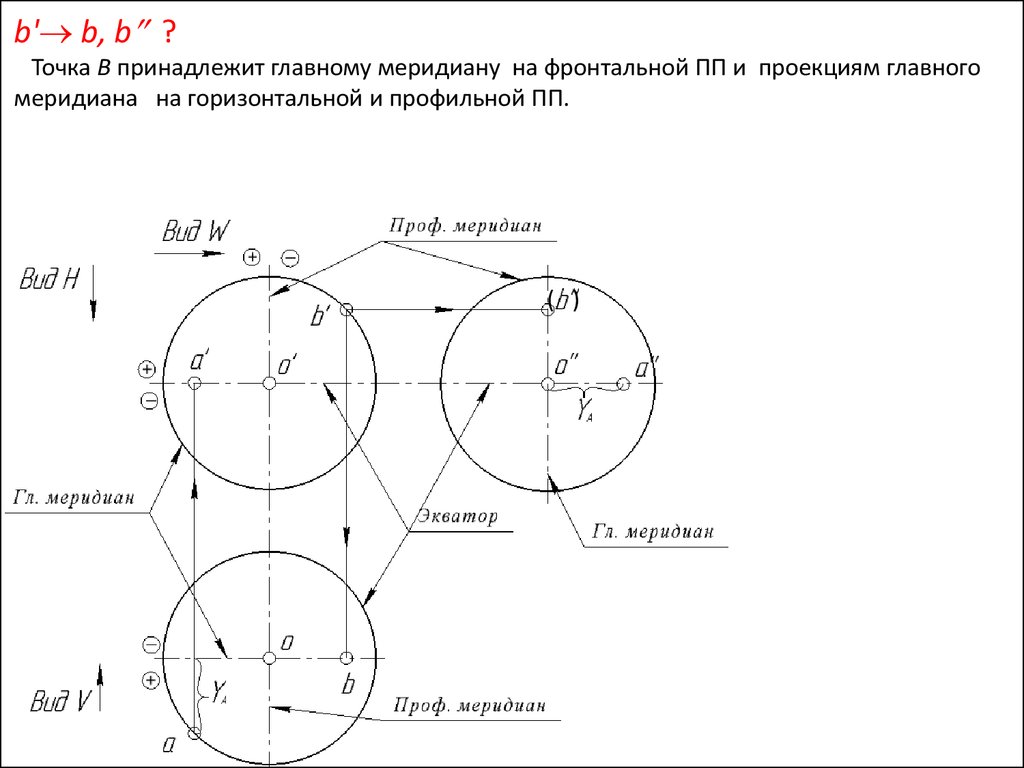
51.
b' b, b ?Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного
меридиана на горизонтальной и профильной ПП.
52.
b' b, b ?Точка В принадлежит главному меридиану на фронтальной ПП и проекциям главного
меридиана на горизонтальной и профильной ПП.
( )
53.
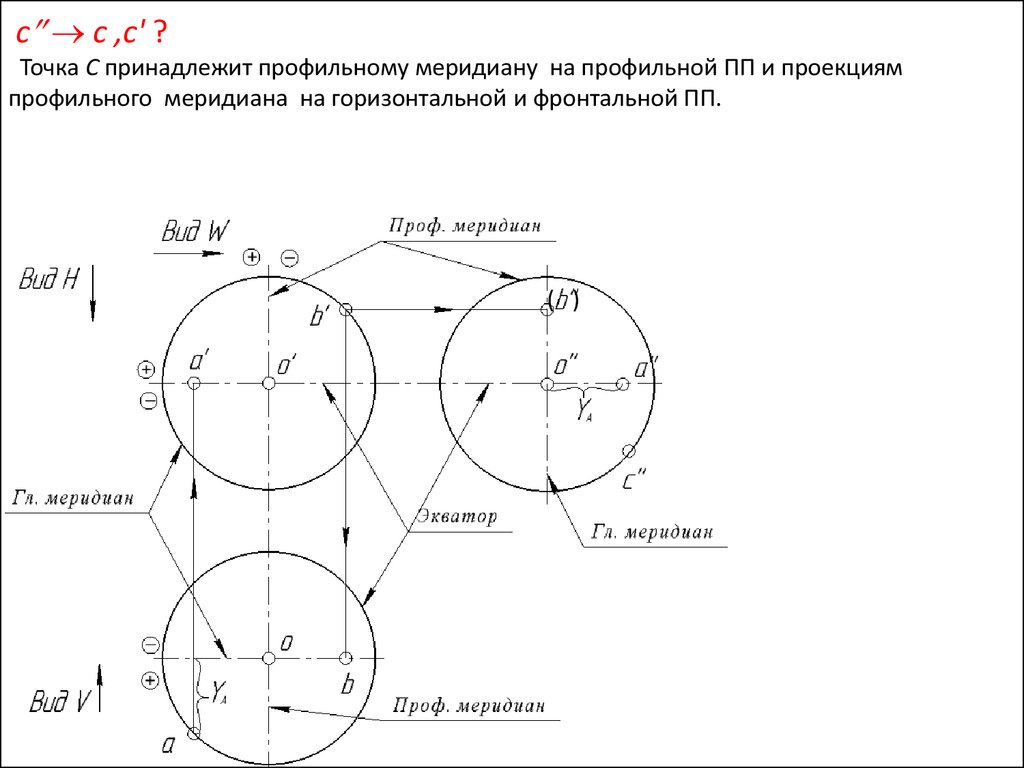
c c ,c' ?Точка С принадлежит профильному меридиану на профильной ПП и проекциям
профильного меридиана на горизонтальной и фронтальной ПП.
( )
54.
c c ,c' ?Точка С принадлежит профильному меридиану на профильной ПП и проекциям
профильного меридиана на горизонтальной и фронтальной ПП.
( )
( )
55.
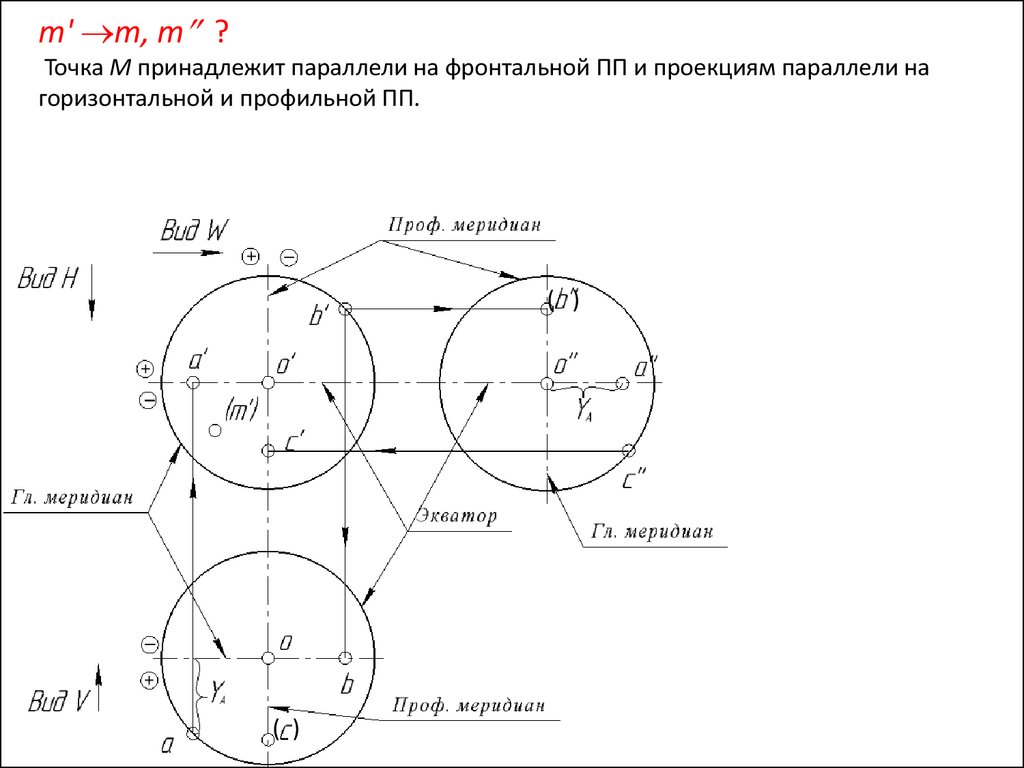
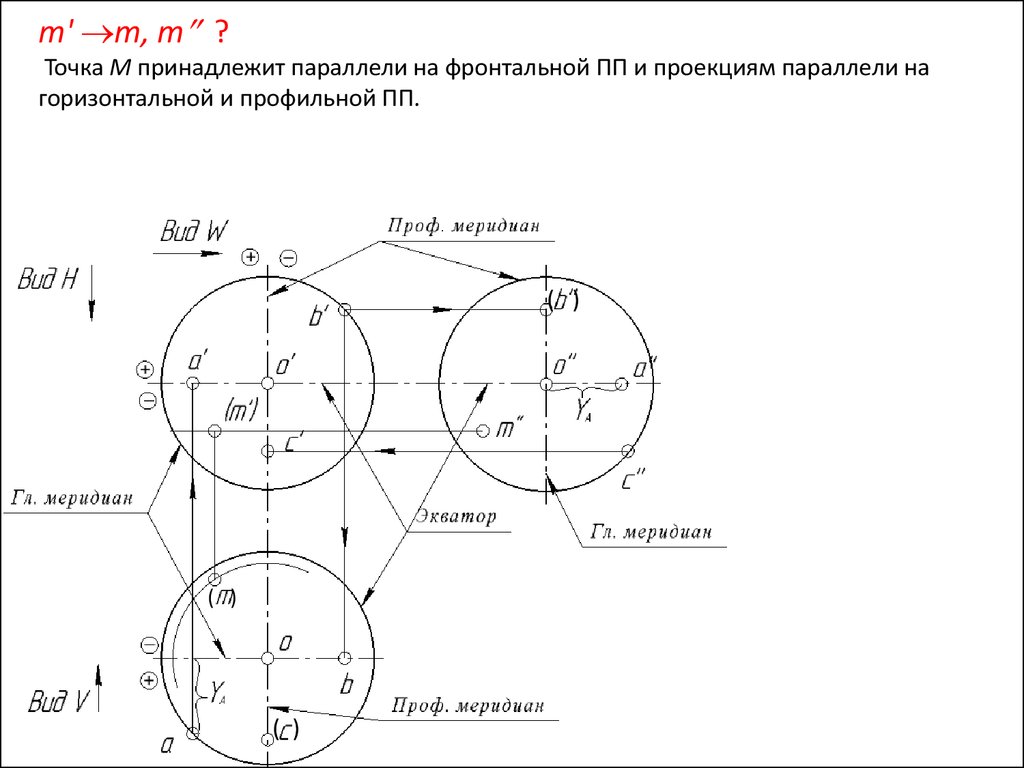
m' m, m ?Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на
горизонтальной и профильной ПП.
( )
( )
56.
m' m, m ?Точка М принадлежит параллели на фронтальной ПП и проекциям параллели на
горизонтальной и профильной ПП.
( )
( )
( )
57.
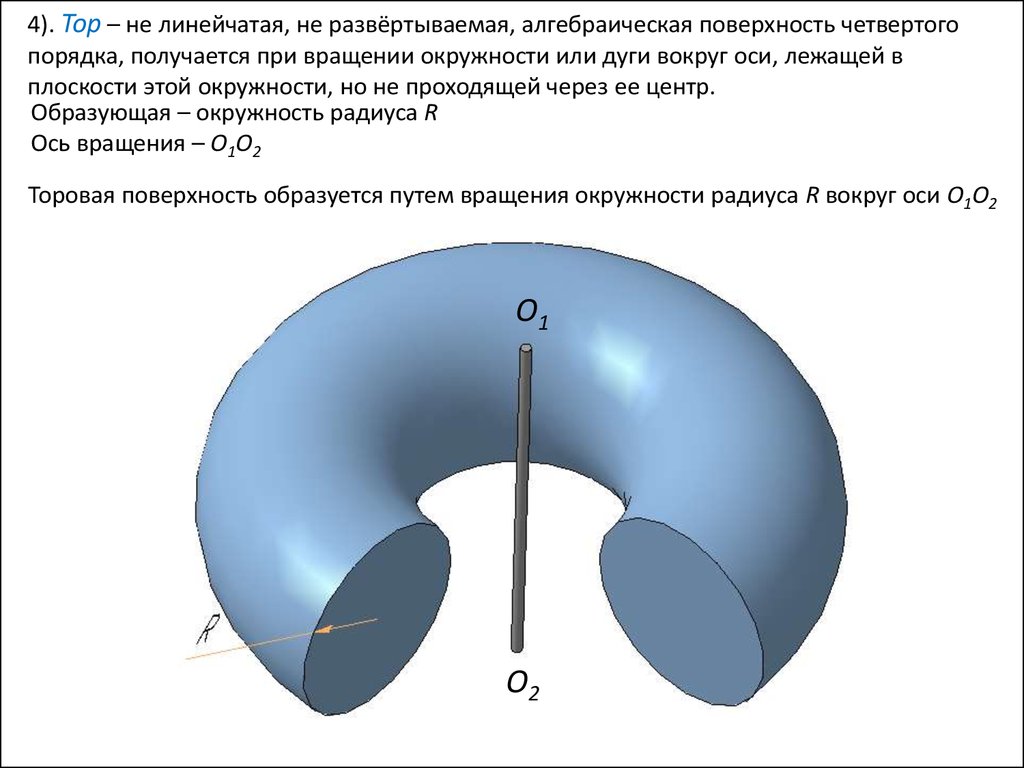
4). Тор – не линейчатая, не развёртываемая, алгебраическая поверхность четвертогопорядка, получается при вращении окружности или дуги вокруг оси, лежащей в
плоскости этой окружности, но не проходящей через ее центр.
Образующая – окружность радиуса R
Ось вращения – О1О2
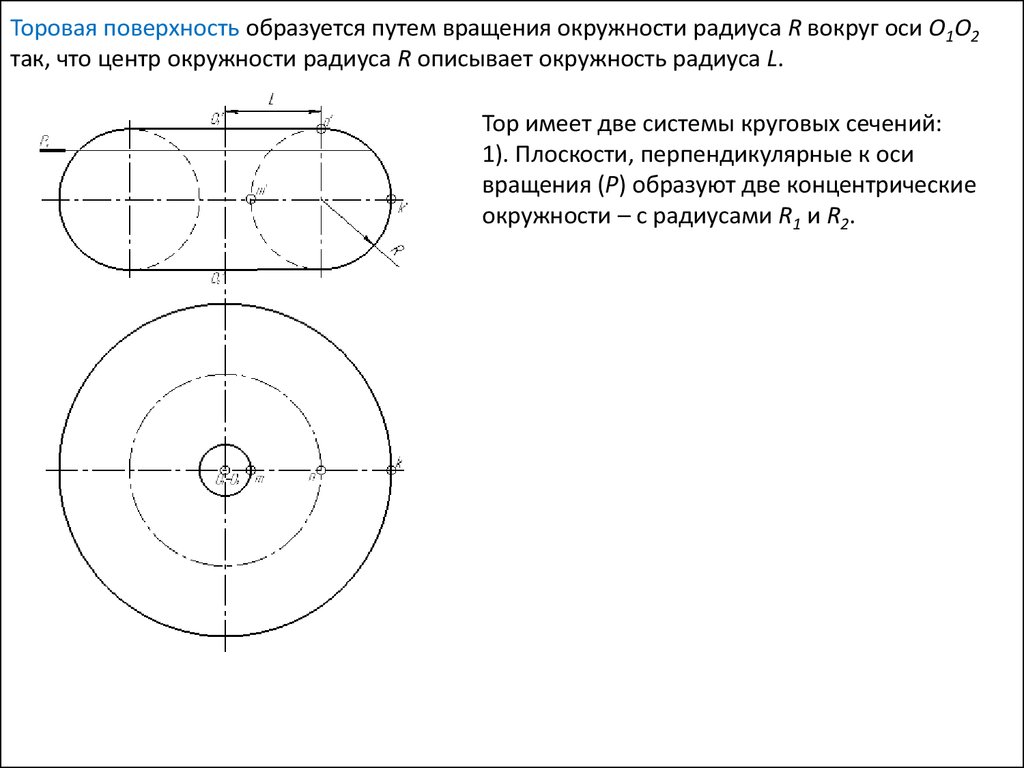
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2
О1
О2
58.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Образующая – окружность радиуса R
Ось вращения – О1О2
59.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Образующая – окружность радиуса R
Ось вращения – О1О2
60.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Образующая – окружность радиуса R
Ось вращения – О1О2
Любая точка образующей окружности (M, N, K)
при вращении вокруг оси О1О2 перемещается по
окружности своего радиуса.
61.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Образующая – окружность радиуса R
Ось вращения – О1О2
Любая точка образующей окружности (M, N, K)
при вращении вокруг оси О1О2 перемещается по
окружности своего радиуса.
Горизонтальная проекция торовой поверхности
– две концентрические окружности,
фронтальная – справа и слева ограничена
дугами полуокружности радиуса R образующей
окружности.
62.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
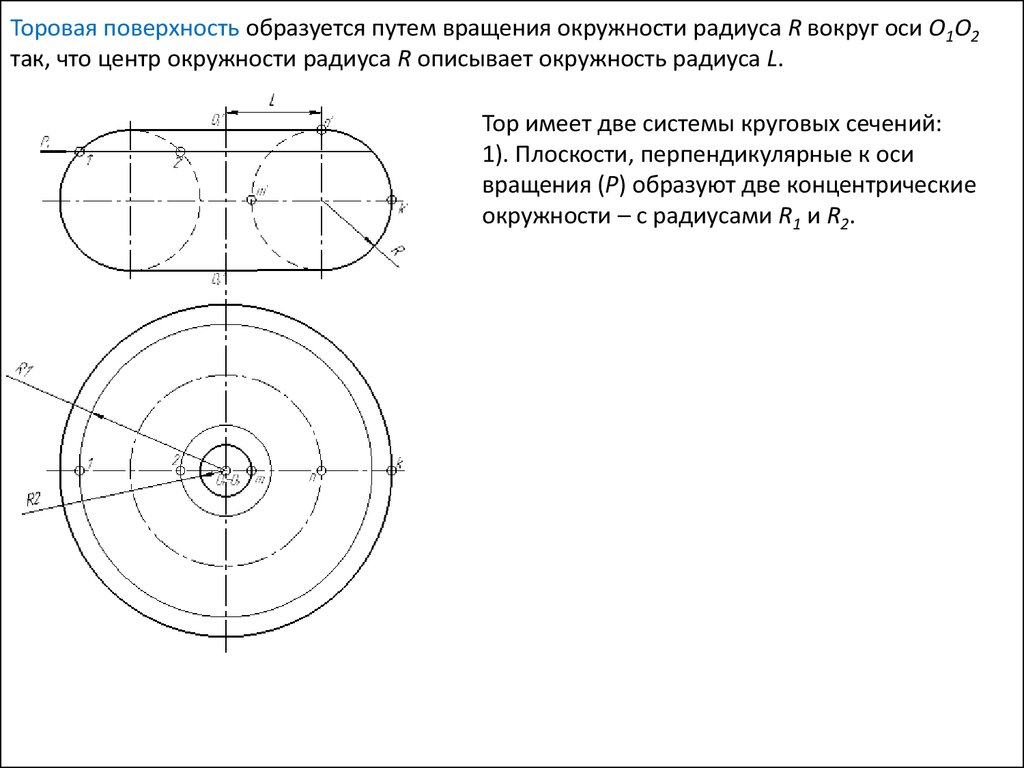
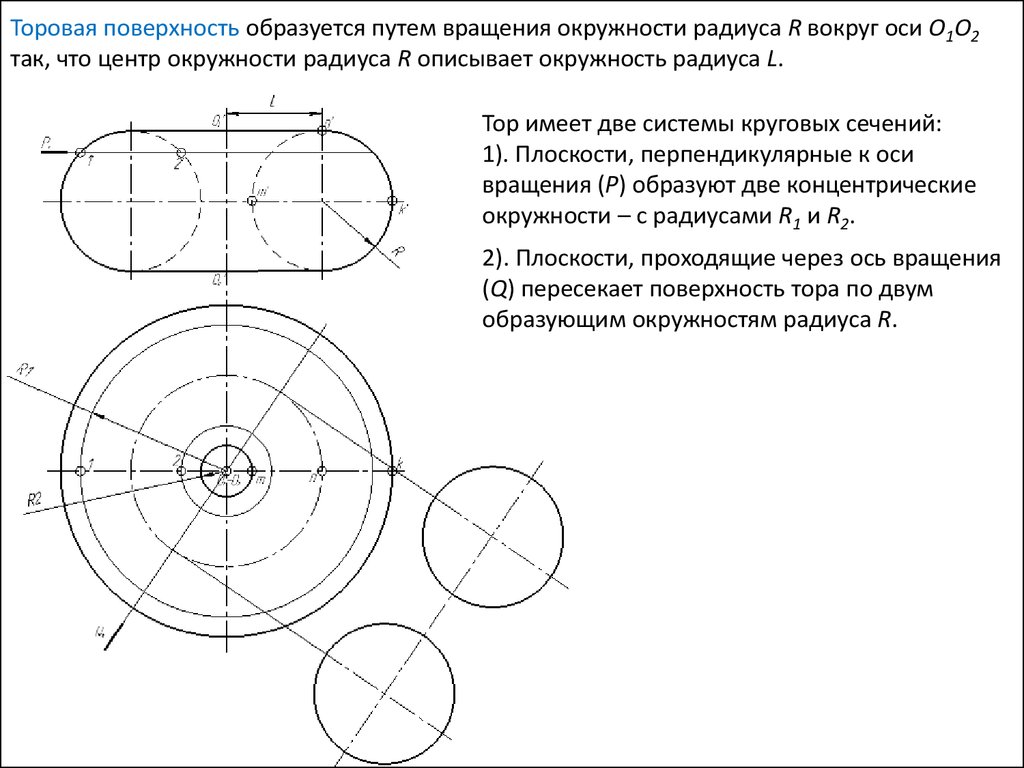
Тор имеет две системы круговых сечений:
1). Плоскости, перпендикулярные к оси
вращения (Р) образуют две концентрические
окружности – с радиусами R1 и R2.
63.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Тор имеет две системы круговых сечений:
1). Плоскости, перпендикулярные к оси
вращения (Р) образуют две концентрические
окружности – с радиусами R1 и R2.
64.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Тор имеет две системы круговых сечений:
1). Плоскости, перпендикулярные к оси
вращения (Р) образуют две концентрические
окружности – с радиусами R1 и R2.
2). Плоскости, проходящие через ось вращения
(Q) пересекает поверхность тора по двум
образующим окружностям радиуса R.
65.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Положение точки на поверхности тора
определяется по признаку принадлежности
точки линии данной поверхности.
Например, если задана фронтальная
проекция точки А и требуется построить
горизонтальную проекцию точки, то, как в
случае любой поверхности вращения, через
точку следует провести окружность,
построить проекции этой окружности, и
найти на одной из них недостающую
проекцию точки.
66.
Торовая поверхность образуется путем вращения окружности радиуса R вокруг оси О1О2так, что центр окружности радиуса R описывает окружность радиуса L.
Положение точки на поверхности тора
определяется по признаку принадлежности
точки линии данной поверхности.
Например, если задана фронтальная
проекция точки А и требуется построить
горизонтальную проекцию точки, то, как в
случае любой поверхности вращения, через
точку следует провести окружность,
построить проекции этой окружности, и
найти на одной из них недостающую
проекцию точки.
67.
Вид торовой поверхности зависит от соотношения величин L и R:Если L > R, то тор называют открытым.
При L = R, то тор называют закрытый или замкнутый.
Если L < R, то тор называют самопересекающийся.
Замкнутый
68.
Самопересекающийся69.
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ70.
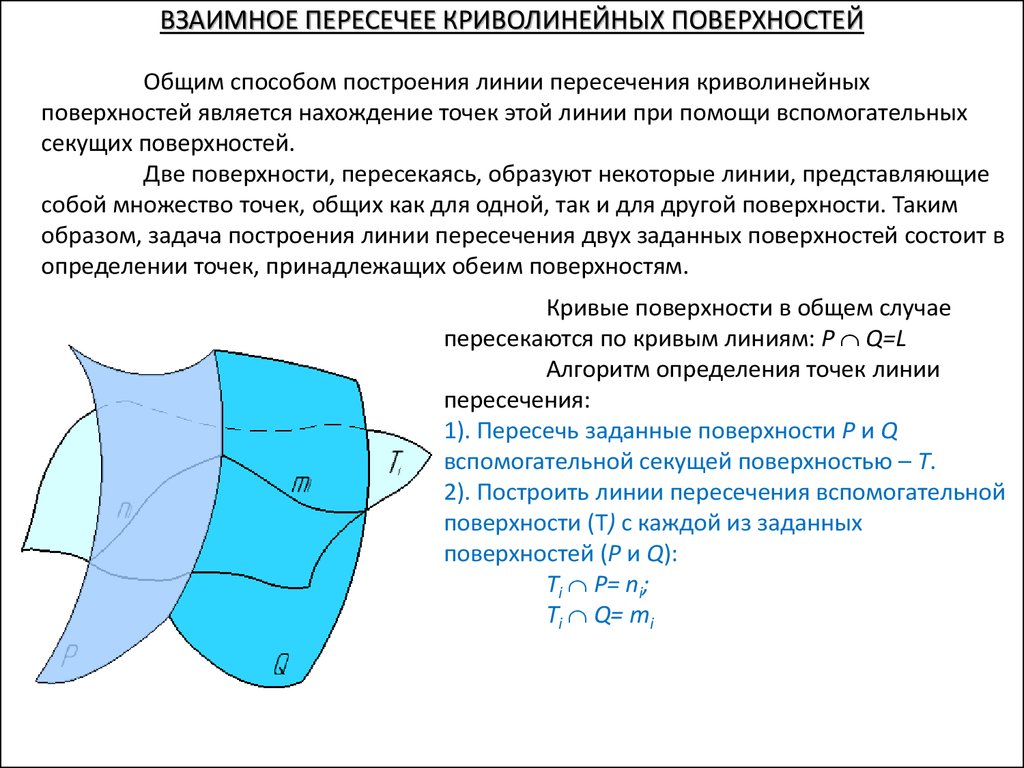
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙОбщим способом построения линии пересечения криволинейных
поверхностей является нахождение точек этой линии при помощи вспомогательных
секущих поверхностей.
Две поверхности, пересекаясь, образуют некоторые линии, представляющие
собой множество точек, общих как для одной, так и для другой поверхности. Таким
образом, задача построения линии пересечения двух заданных поверхностей состоит в
определении точек, принадлежащих обеим поверхностям.
Кривые поверхности в общем случае
пересекаются по кривым линиям: P Q=L
71.
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙОбщим способом построения линии пересечения криволинейных
поверхностей является нахождение точек этой линии при помощи вспомогательных
секущих поверхностей.
Две поверхности, пересекаясь, образуют некоторые линии, представляющие
собой множество точек, общих как для одной, так и для другой поверхности. Таким
образом, задача построения линии пересечения двух заданных поверхностей состоит в
определении точек, принадлежащих обеим поверхностям.
Кривые поверхности в общем случае
пересекаются по кривым линиям: P Q=L
Алгоритм определения точек линии
пересечения:
1). Пересечь заданные поверхности P и Q
вспомогательной секущей поверхностью – T.
72.
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙОбщим способом построения линии пересечения криволинейных
поверхностей является нахождение точек этой линии при помощи вспомогательных
секущих поверхностей.
Две поверхности, пересекаясь, образуют некоторые линии, представляющие
собой множество точек, общих как для одной, так и для другой поверхности. Таким
образом, задача построения линии пересечения двух заданных поверхностей состоит в
определении точек, принадлежащих обеим поверхностям.
Кривые поверхности в общем случае
пересекаются по кривым линиям: P Q=L
Алгоритм определения точек линии
пересечения:
1). Пересечь заданные поверхности P и Q
вспомогательной секущей поверхностью – T.
2). Построить линии пересечения вспомогательной
поверхности (T) с каждой из заданных
поверхностей (P и Q):
Ti P= ni;
73.
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙОбщим способом построения линии пересечения криволинейных
поверхностей является нахождение точек этой линии при помощи вспомогательных
секущих поверхностей.
Две поверхности, пересекаясь, образуют некоторые линии, представляющие
собой множество точек, общих как для одной, так и для другой поверхности. Таким
образом, задача построения линии пересечения двух заданных поверхностей состоит в
определении точек, принадлежащих обеим поверхностям.
Кривые поверхности в общем случае
пересекаются по кривым линиям: P Q=L
Алгоритм определения точек линии
пересечения:
1). Пересечь заданные поверхности P и Q
вспомогательной секущей поверхностью – T.
2). Построить линии пересечения вспомогательной
поверхности (T) с каждой из заданных
поверхностей (P и Q):
Ti P= ni;
Ti Q= mi
74.
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙОбщим способом построения линии пересечения криволинейных
поверхностей является нахождение точек этой линии при помощи вспомогательных
секущих поверхностей.
Две поверхности, пересекаясь, образуют некоторые линии, представляющие
собой множество точек, общих как для одной, так и для другой поверхности. Таким
образом, задача построения линии пересечения двух заданных поверхностей состоит в
определении точек, принадлежащих обеим поверхностям.
Кривые поверхности в общем случае
пересекаются по кривым линиям: P Q=L
Алгоритм определения точек линии
пересечения:
1). Пересечь заданные поверхности P и Q
вспомогательной секущей поверхностью – T.
2). Построить линии пересечения вспомогательной
поверхности (T) с каждой из заданных
поверхностей (P и Q):
Ti P= ni;
Ti Q= mi
3). Построить точку пересечения полученных линий
пересечения:
ni mi= Ki
75.
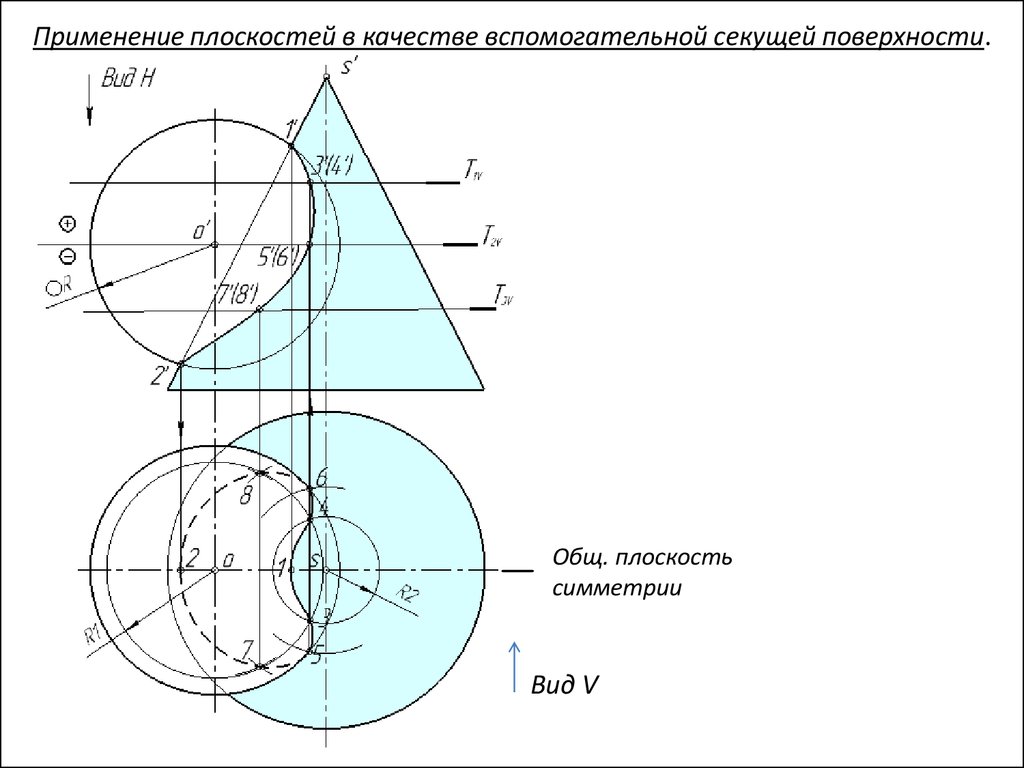
Применение плоскостей в качестве вспомогательной секущей поверхности.План решения задачи:
I). Определение характерных точек:
- наивысшей и наинизшей;
- точки, определяющие видимость
линии пересечения.
II). Определение промежуточных точек по
разработанному алгоритму.
III). Определение видимости линии
пересечения.
76.
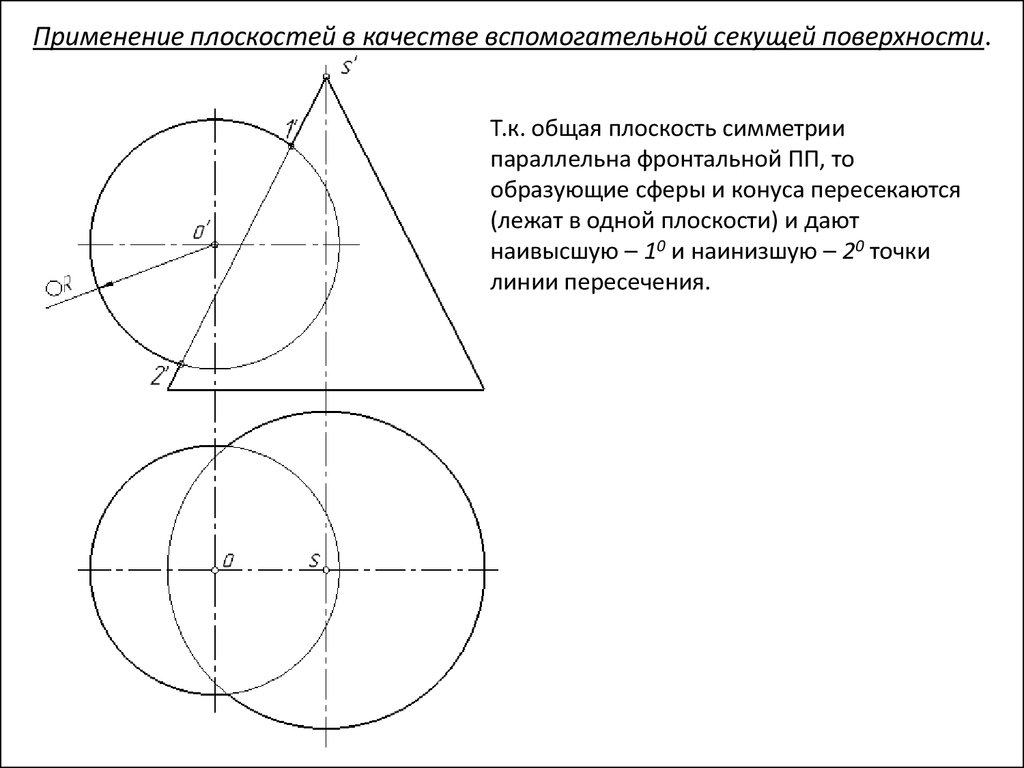
Применение плоскостей в качестве вспомогательной секущей поверхности.Т.к. общая плоскость симметрии
параллельна фронтальной ПП, то
образующие сферы и конуса пересекаются
(лежат в одной плоскости) и дают
наивысшую – 10 и наинизшую – 20 точки
линии пересечения.
77.
Применение плоскостей в качестве вспомогательной секущей поверхности.Т.к. общая плоскость симметрии
параллельна фронтальной ПП, то
образующие сферы и конуса пересекаются
(лежат в одной плоскости) и дают
наивысшую – 10 и наинизшую – 20 точки
линии пересечения.
78.
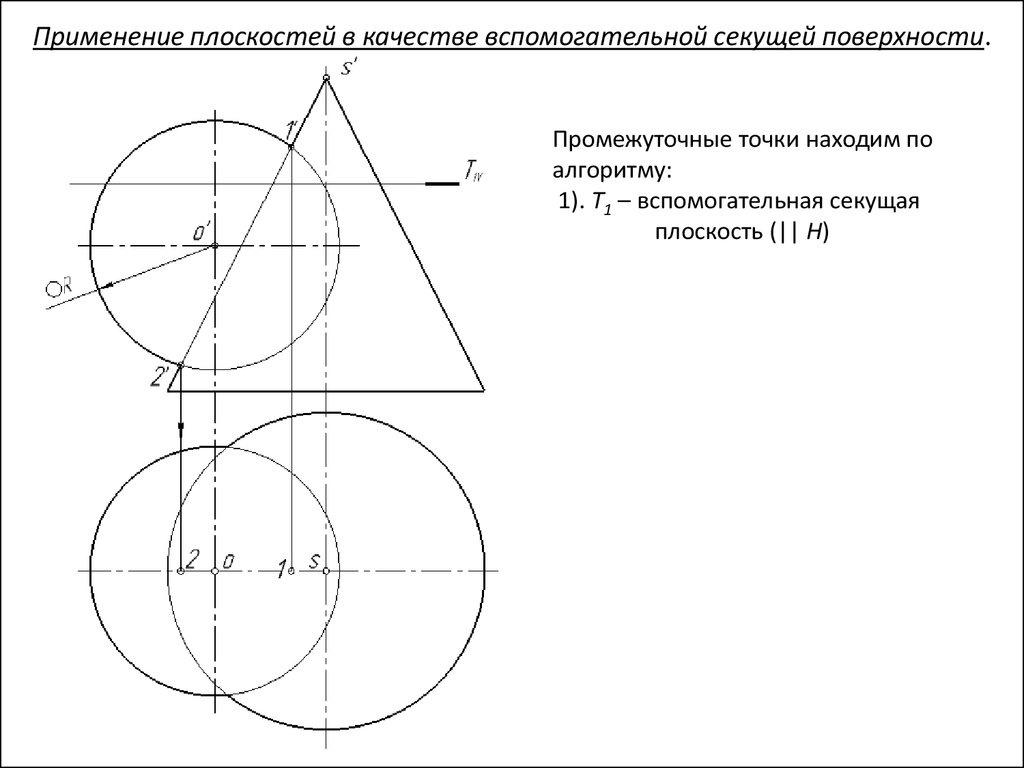
Применение плоскостей в качестве вспомогательной секущей поверхности.Промежуточные точки находим по
алгоритму:
1). T1 – вспомогательная секущая
плоскость (|| H)
79.
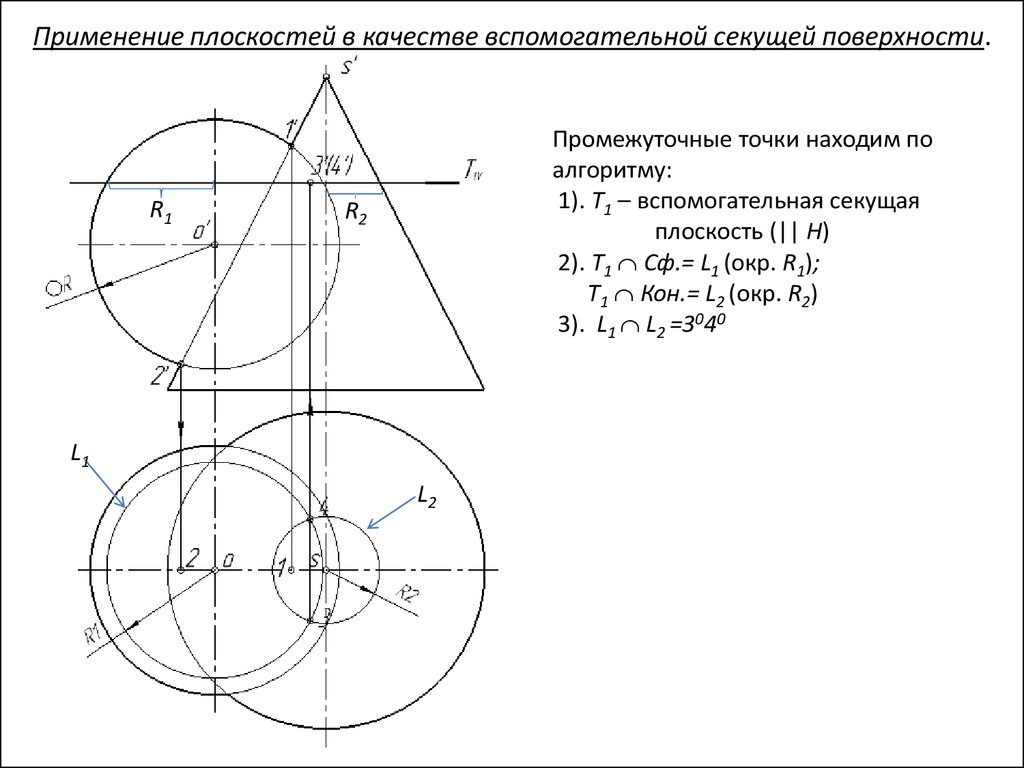
Применение плоскостей в качестве вспомогательной секущей поверхности.R1
Промежуточные точки находим по
алгоритму:
1). T1 – вспомогательная секущая
плоскость (|| H)
2). T1 Сф.= L1 (окр. R1);
T1 Кон.= L2 (окр. R2)
3). L1 L2 =3040
R2
L1
L2
80.
Применение плоскостей в качестве вспомогательной секущей поверхности.Вводя новые вспомогательные
горизонтальные плоскости и повторяя
приведенные построения, можно найти
достаточное количество точек, соединив
которые плавной кривой - получить
проекции линии пересечения.
81.
Применение плоскостей в качестве вспомогательной секущей поверхности.Вводя новые вспомогательные
горизонтальные плоскости и повторяя
приведенные построения, можно найти
достаточное количество точек, соединив
которые плавной кривой - получить
проекции линии пересечения.
82.
Применение плоскостей в качестве вспомогательной секущей поверхности.Вводя новые вспомогательные
горизонтальные плоскости и повторяя
приведенные построения, можно найти
достаточное количество точек, соединив
которые плавной кривой - получить
проекции линии пересечения.
83.
Применение плоскостей в качестве вспомогательной секущей поверхности.Вводя новые вспомогательные
горизонтальные плоскости и повторяя
приведенные построения, можно найти
достаточное количество точек, соединив
которые плавной кривой - получить
проекции линии пересечения.
84.
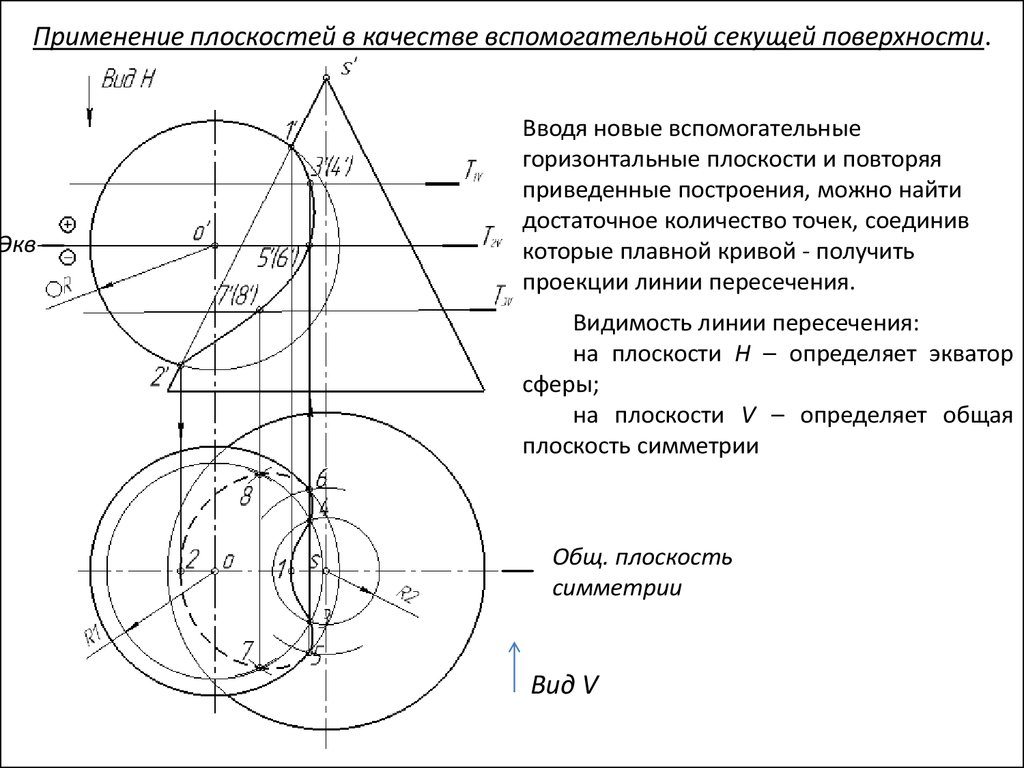
Применение плоскостей в качестве вспомогательной секущей поверхности.Экв
Вводя новые вспомогательные
горизонтальные плоскости и повторяя
приведенные построения, можно найти
достаточное количество точек, соединив
которые плавной кривой - получить
проекции линии пересечения.
Видимость линии пересечения:
на плоскости Н – определяет экватор
сферы;
на плоскости V – определяет общая
плоскость симметрии
Общ. плоскость
симметрии
Вид V
85.
Применение плоскостей в качестве вспомогательной секущей поверхности.Общ. плоскость
симметрии
Вид V
86.
Общаяпл-ть симметрии
87.
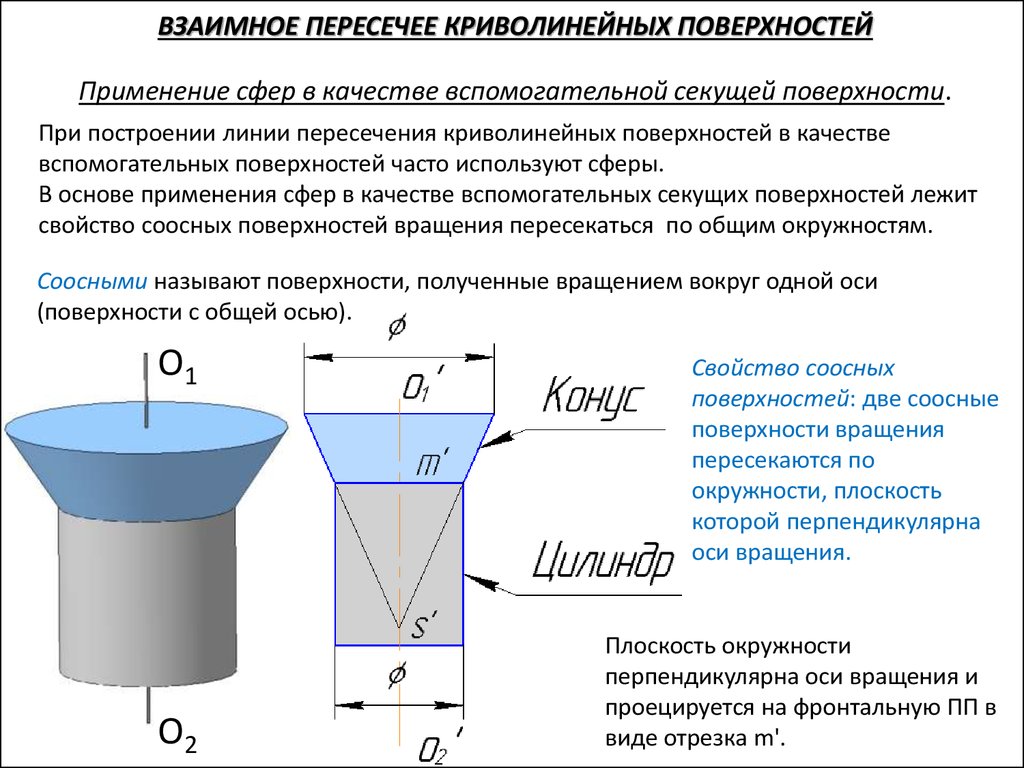
ВЗАИМНОЕ ПЕРЕСЕЧЕЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙПрименение сфер в качестве вспомогательной секущей поверхности.
При построении линии пересечения криволинейных поверхностей в качестве
вспомогательных поверхностей часто используют сферы.
В основе применения сфер в качестве вспомогательных секущих поверхностей лежит
свойство соосных поверхностей вращения пересекаться по общим окружностям.
Соосными называют поверхности, полученные вращением вокруг одной оси
(поверхности с общей осью).
О1
О2
Свойство соосных
поверхностей: две соосные
поверхности вращения
пересекаются по
окружности, плоскость
которой перпендикулярна
оси вращения.
Плоскость окружности
перпендикулярна оси вращения и
проецируется на фронтальную ПП в
виде отрезка m'.
88.
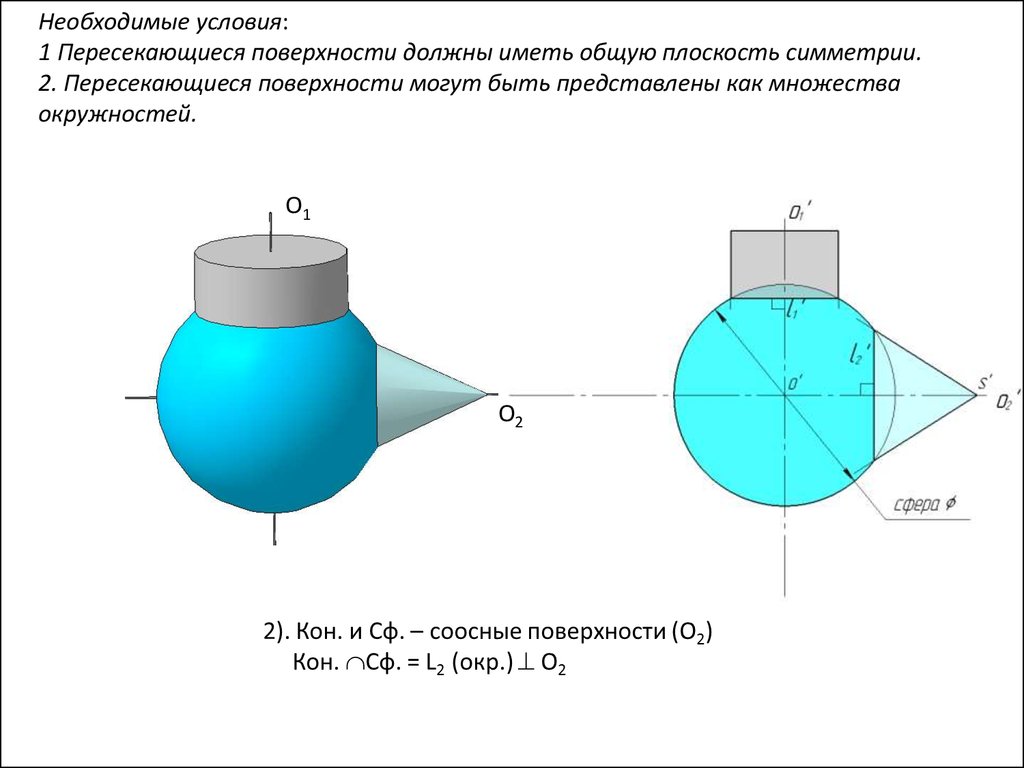
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
89.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
1). Цил. и Сф. – соосные поверхности (O1)
90.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
1). Цил. и Сф. – соосные поверхности (O1)
Цил. Сф. = L1 (окр.) O1
91.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
2). Кон. и Сф. – соосные поверхности (O2)
92.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
93.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
3). Тор и Сф. – соосные поверхности (O1)
94.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
3). Тор и Сф. – соосные поверхности (O1)
Тор Сф = L3 (окр.) O1
95.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
4). Сф. и Сф.1 – соосные поверхности (O2)
96.
Необходимые условия:1 Пересекающиеся поверхности должны иметь общую плоскость симметрии.
2. Пересекающиеся поверхности могут быть представлены как множества
окружностей.
O1
O2
4). Сф. и Сф.1 – соосные поверхности (O2)
Сф. Сф.1 = L4 (окр.) O2
97.
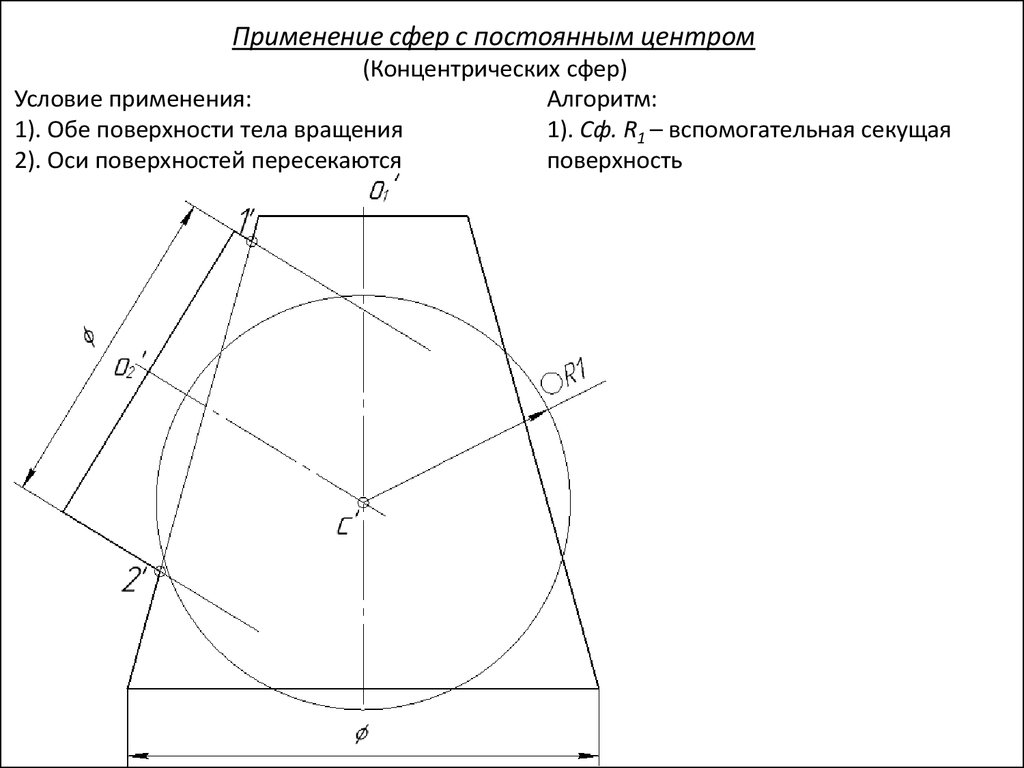
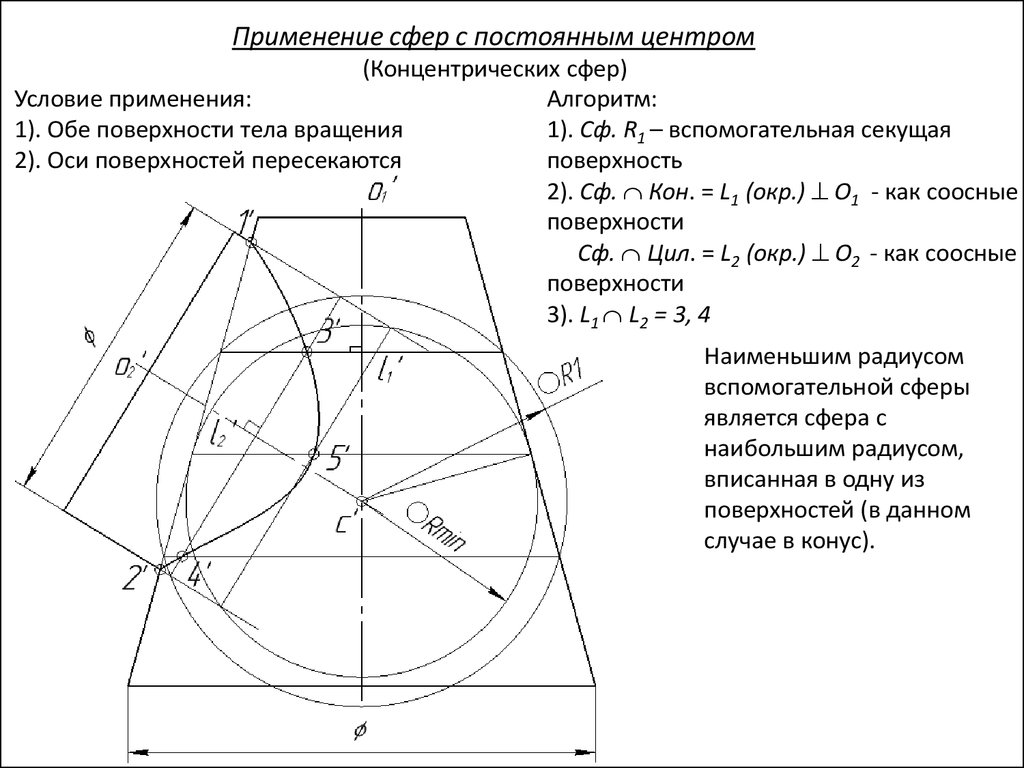
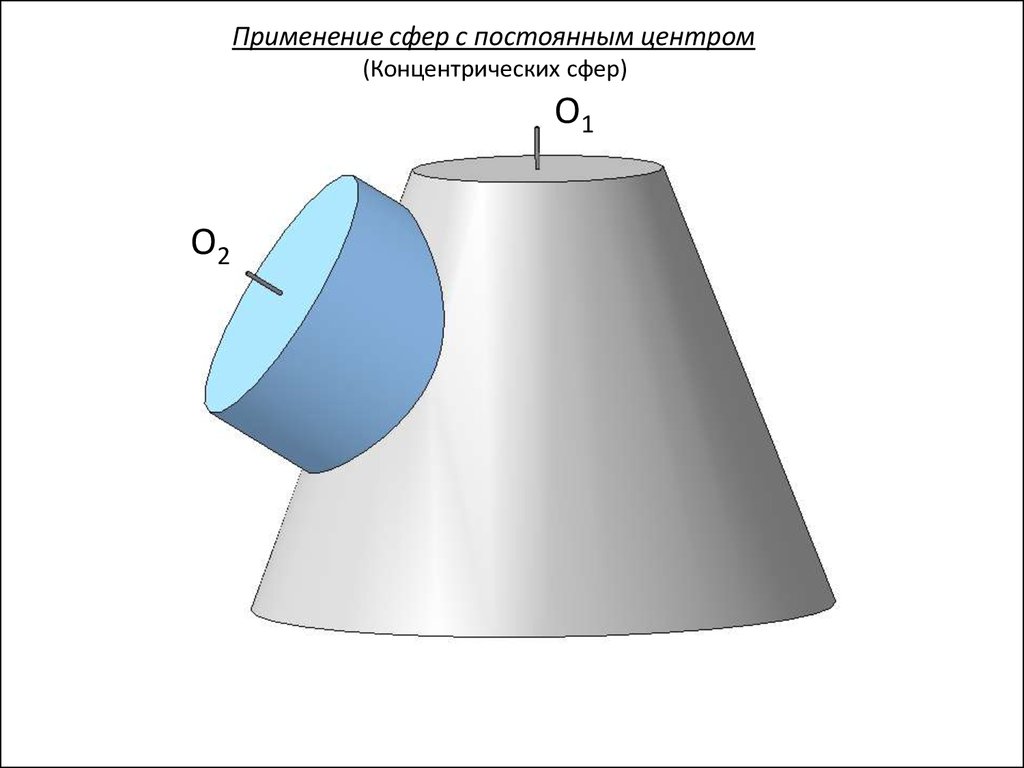
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
1). Обе поверхности тела вращения
2). Оси поверхностей пересекаются
Центр вспомогательных секущих сфер
находится в точке пересечения осей O1 и O2
заданных поверхностей.
98.
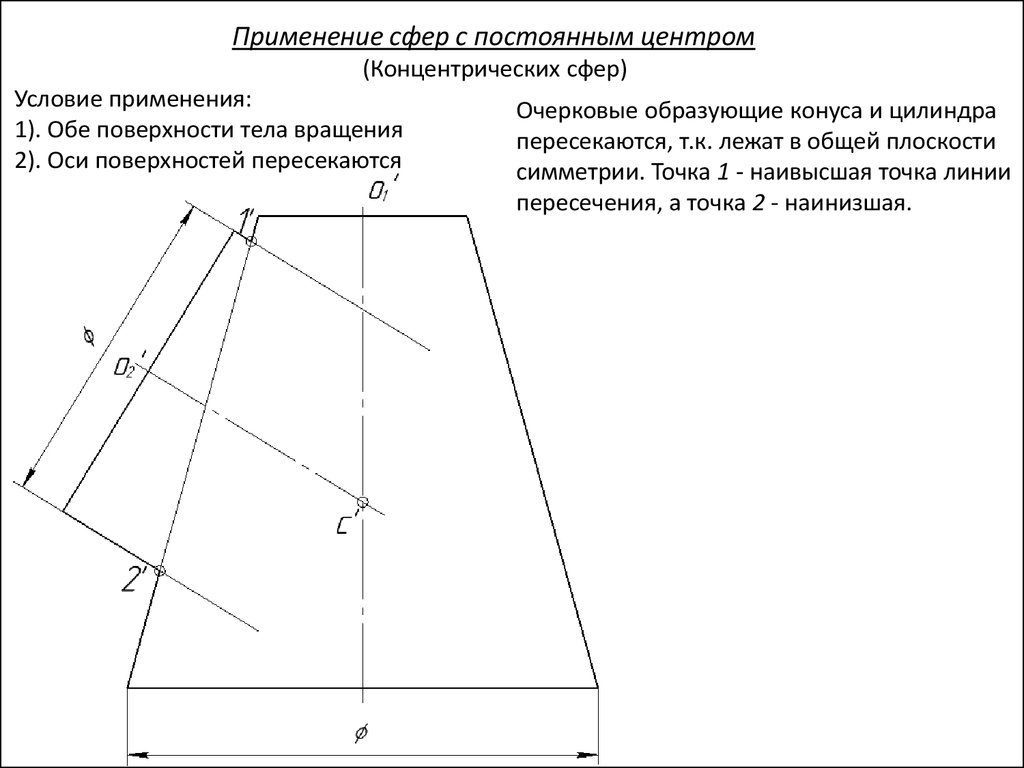
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
1). Обе поверхности тела вращения
2). Оси поверхностей пересекаются
Очерковые образующие конуса и цилиндра
пересекаются, т.к. лежат в общей плоскости
симметрии. Точка 1 - наивысшая точка линии
пересечения, а точка 2 - наинизшая.
99.
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
100.
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
101.
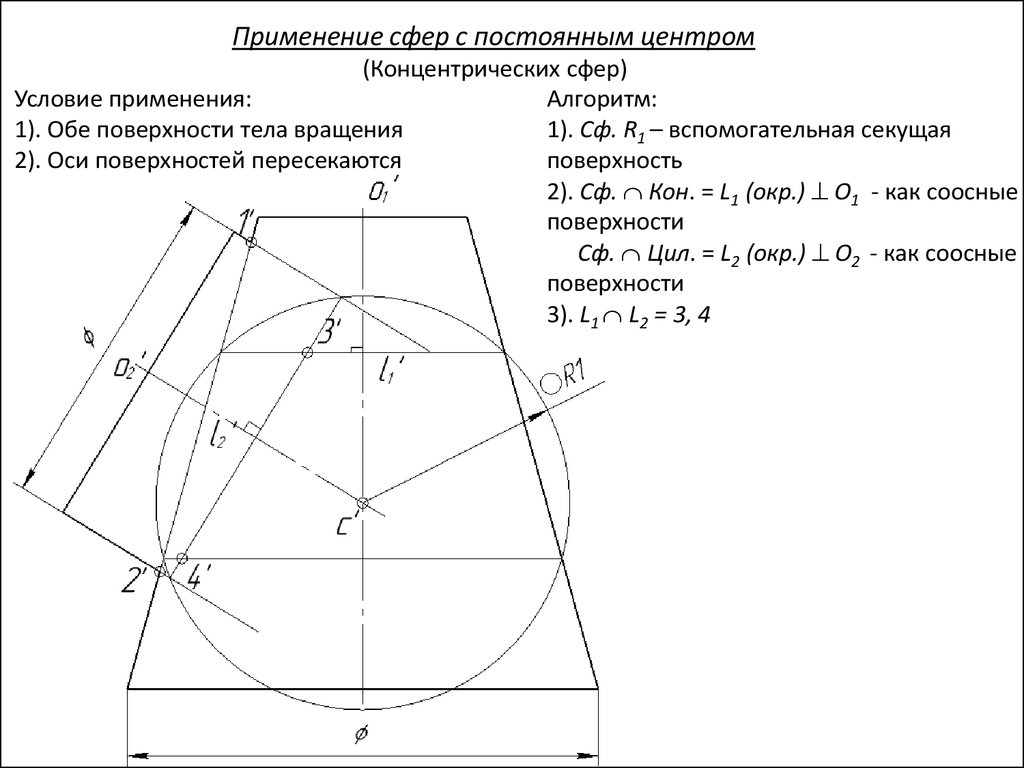
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
3). L1 L2 = 3, 4
102.
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
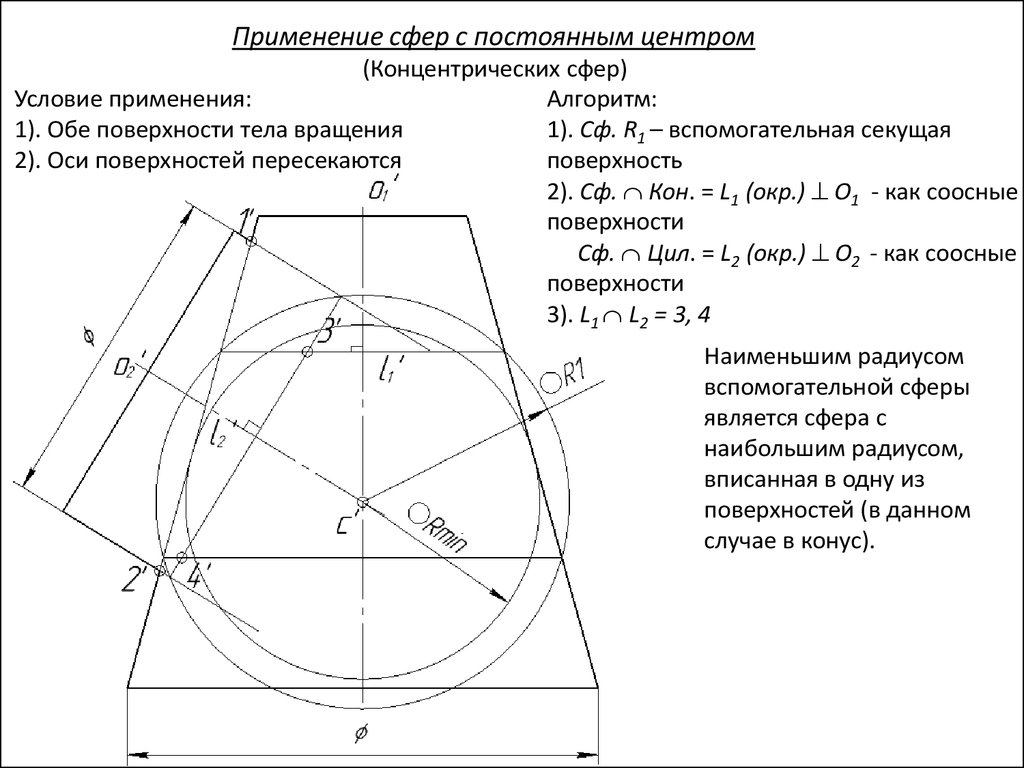
3). L1 L2 = 3, 4
Наименьшим радиусом
вспомогательной сферы
является сфера с
наибольшим радиусом,
вписанная в одну из
поверхностей (в данном
случае в конус).
103.
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
3). L1 L2 = 3, 4
Наименьшим радиусом
вспомогательной сферы
является сфера с
наибольшим радиусом,
вписанная в одну из
поверхностей (в данном
случае в конус).
104.
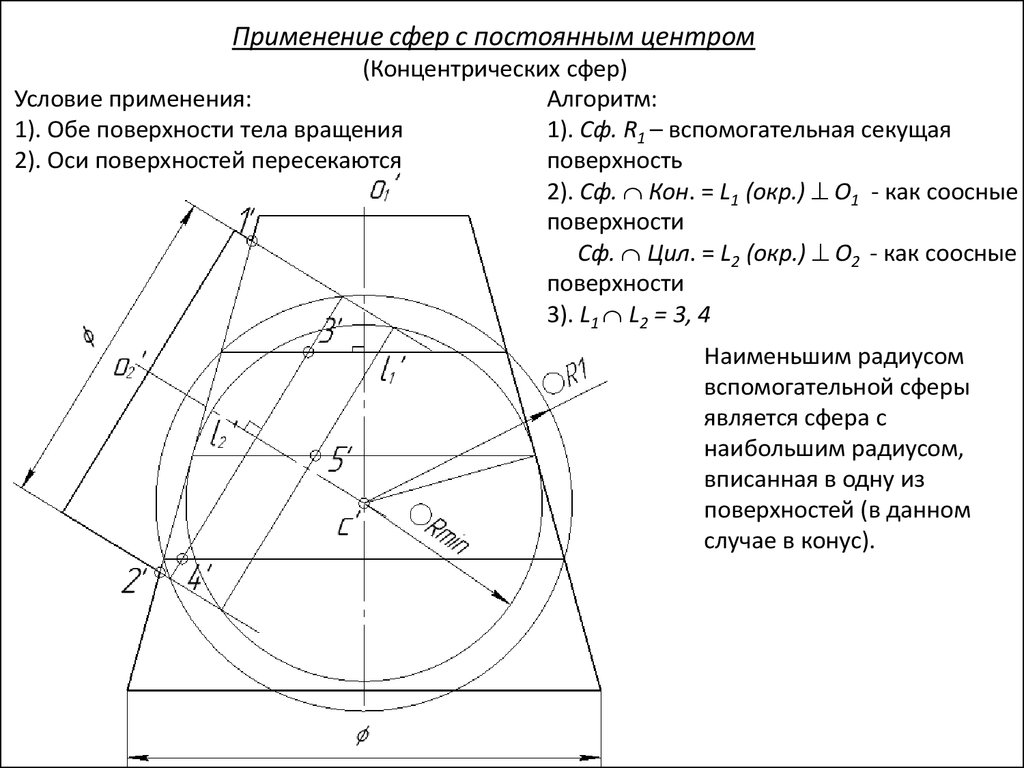
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
3). L1 L2 = 3, 4
Наименьшим радиусом
вспомогательной сферы
является сфера с
наибольшим радиусом,
вписанная в одну из
поверхностей (в данном
случае в конус).
105.
Применение сфер с постоянным центром(Концентрических сфер)
Условие применения:
Алгоритм:
1). Обе поверхности тела вращения
1). Сф. R1 – вспомогательная секущая
2). Оси поверхностей пересекаются
поверхность
2). Сф. Кон. = L1 (окр.) O1 - как соосные
поверхности
Сф. Цил. = L2 (окр.) O2 - как соосные
поверхности
3). L1 L2 = 3, 4
Наименьшим радиусом
вспомогательной сферы
является сфера с
наибольшим радиусом,
вписанная в одну из
поверхностей (в данном
случае в конус).
106.
Применение сфер с постоянным центром(Концентрических сфер)
O1
O2
107.
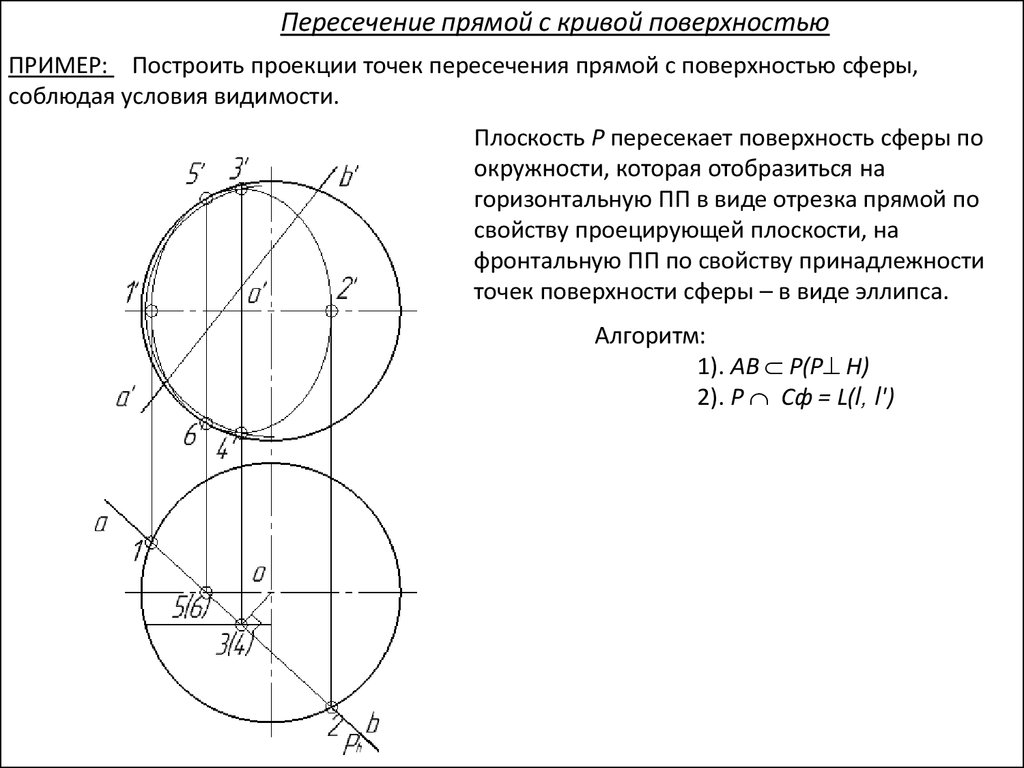
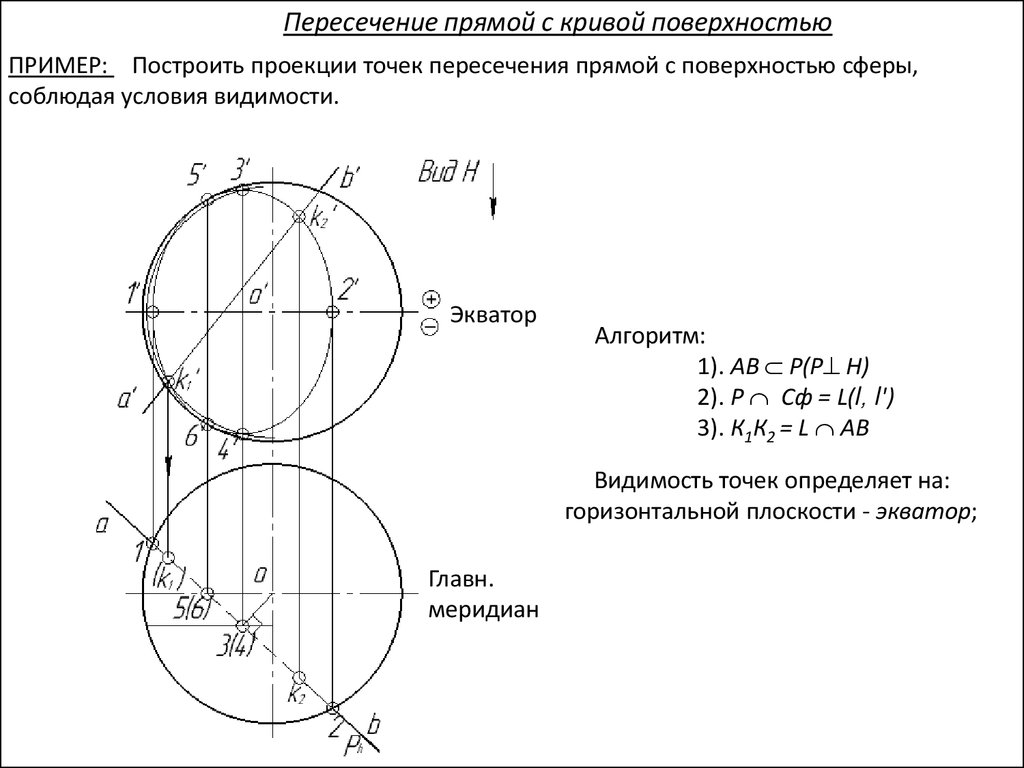
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Плоскость Р пересекает поверхность сферы по
окружности, которая отобразиться на
горизонтальную ПП в виде отрезка прямой по
свойству проецирующей плоскости, на
фронтальную ПП по свойству принадлежности
точек поверхности сферы – в виде эллипса.
Алгоритм:
1). АВ Р(Р H)
108.
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Плоскость Р пересекает поверхность сферы по
окружности, которая отобразиться на
горизонтальную ПП в виде отрезка прямой по
свойству проецирующей плоскости, на
фронтальную ПП по свойству принадлежности
точек поверхности сферы – в виде эллипса.
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
109.
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Плоскость Р пересекает поверхность сферы по
окружности, которая отобразиться на
горизонтальную ПП в виде отрезка прямой по
свойству проецирующей плоскости, на
фронтальную ПП по свойству принадлежности
точек поверхности сферы – в виде эллипса.
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
110.
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Плоскость Р пересекает поверхность сферы по
окружности, которая отобразиться на
горизонтальную ПП в виде отрезка прямой по
свойству проецирующей плоскости, на
фронтальную ПП по свойству принадлежности
точек поверхности сферы – в виде эллипса.
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
111.
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Плоскость Р пересекает поверхность сферы по
окружности, которая отобразиться на
горизонтальную ПП в виде отрезка прямой по
свойству проецирующей плоскости, на
фронтальную ПП по свойству принадлежности
точек поверхности сферы – в виде эллипса.
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
3). К1К2 = L АВ
112.
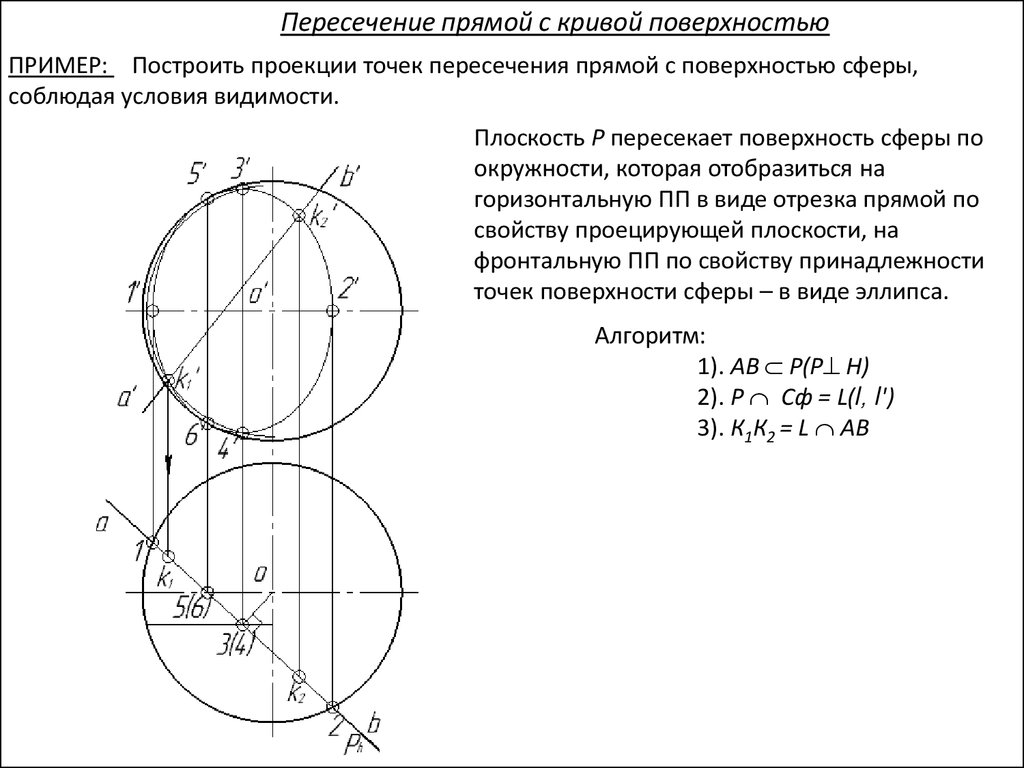
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Экватор
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
3). К1К2 = L АВ
Видимость точек определяет на:
горизонтальной плоскости - экватор;
Главн.
меридиан
113.
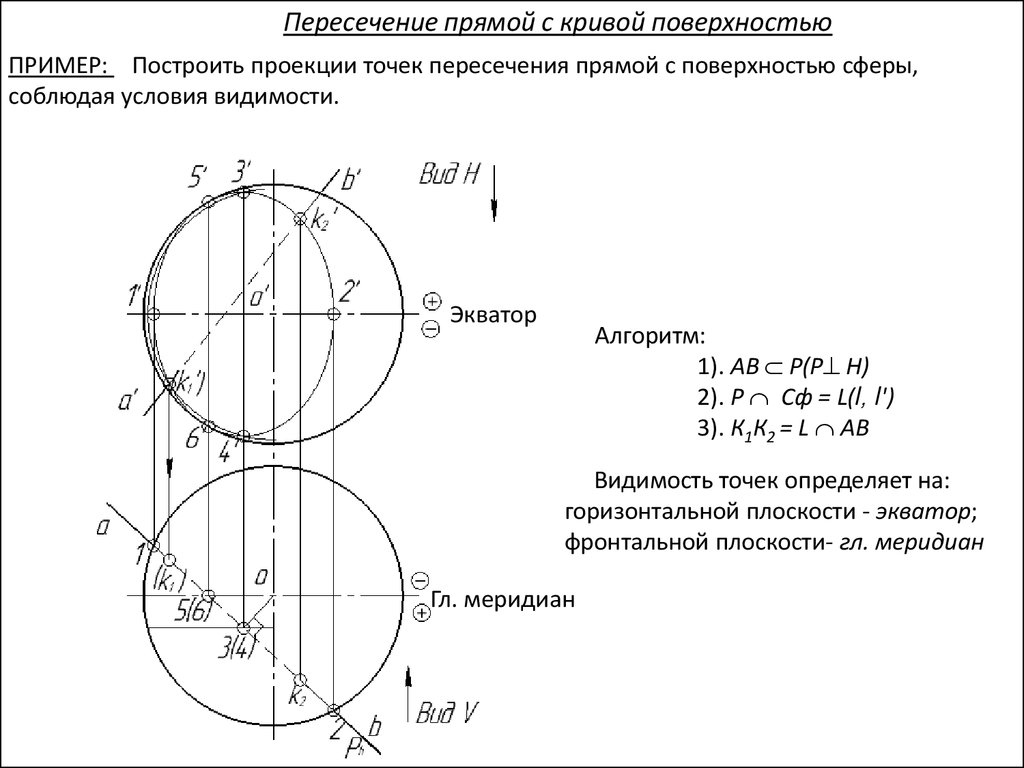
Пересечение прямой с кривой поверхностьюПРИМЕР: Построить проекции точек пересечения прямой с поверхностью сферы,
соблюдая условия видимости.
Экватор
Алгоритм:
1). АВ Р(Р H)
2). Р Сф = L(l, l')
3). К1К2 = L АВ
Видимость точек определяет на:
горизонтальной плоскости - экватор;
фронтальной плоскости- гл. меридиан
Гл. меридиан
114.
МНОГОГРАННИКИ115.
МНОГОГРАННИКИОпределение: Многогранником называется тело, поверхность которого есть
объединение конечного числа многоугольников.
Призма – многогранник, две грани которого n- угольники, лежащие в параллельных
плоскостях, остальные n- граней – параллелограммы.
Ребра - прямые, по которым
пересекаются смежные грани;
Вершина - точка, в которых
пересекаются ребра.
Призма прямая – ребра перпендикулярны основанию.
Призма наклонная – ребра не перпендикулярны основанию.
116.
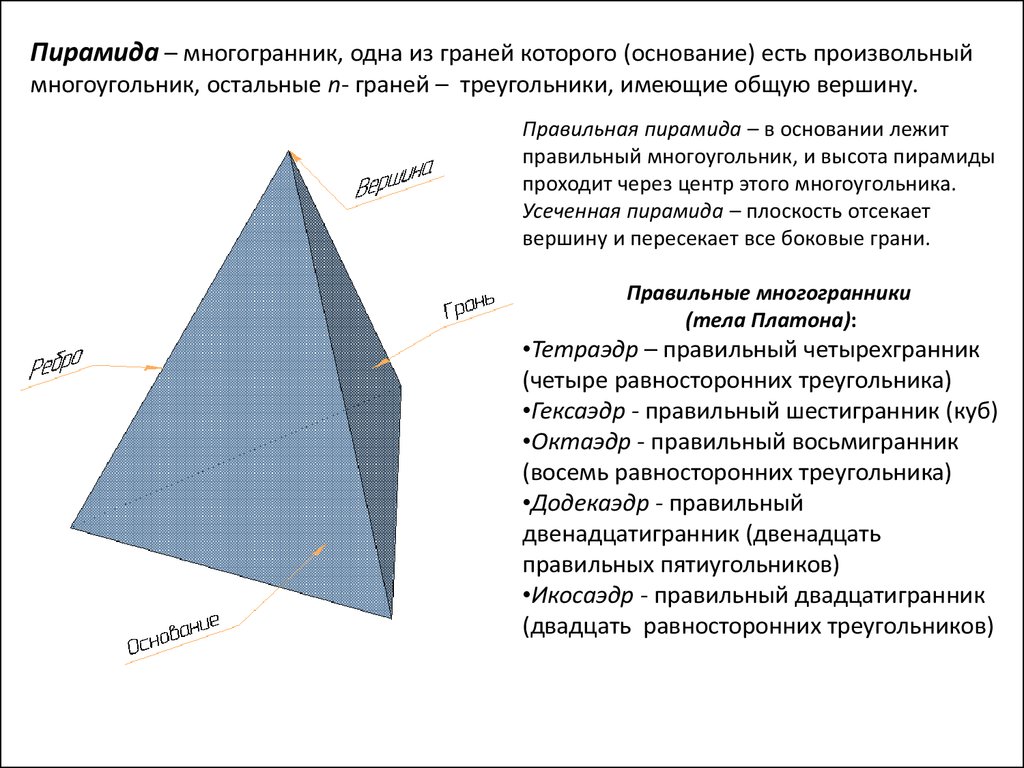
Пирамида – многогранник, одна из граней которого (основание) есть произвольныймногоугольник, остальные n- граней – треугольники, имеющие общую вершину.
Правильная пирамида – в основании лежит
правильный многоугольник, и высота пирамиды
проходит через центр этого многоугольника.
Усеченная пирамида – плоскость отсекает
вершину и пересекает все боковые грани.
Правильные многогранники
(тела Платона):
•Тетраэдр – правильный четырехгранник
(четыре равносторонних треугольника)
•Гексаэдр - правильный шестигранник (куб)
•Октаэдр - правильный восьмигранник
(восемь равносторонних треугольника)
•Додекаэдр - правильный
двенадцатигранник (двенадцать
правильных пятиугольников)
•Икосаэдр - правильный двадцатигранник
(двадцать равносторонних треугольников)
117.
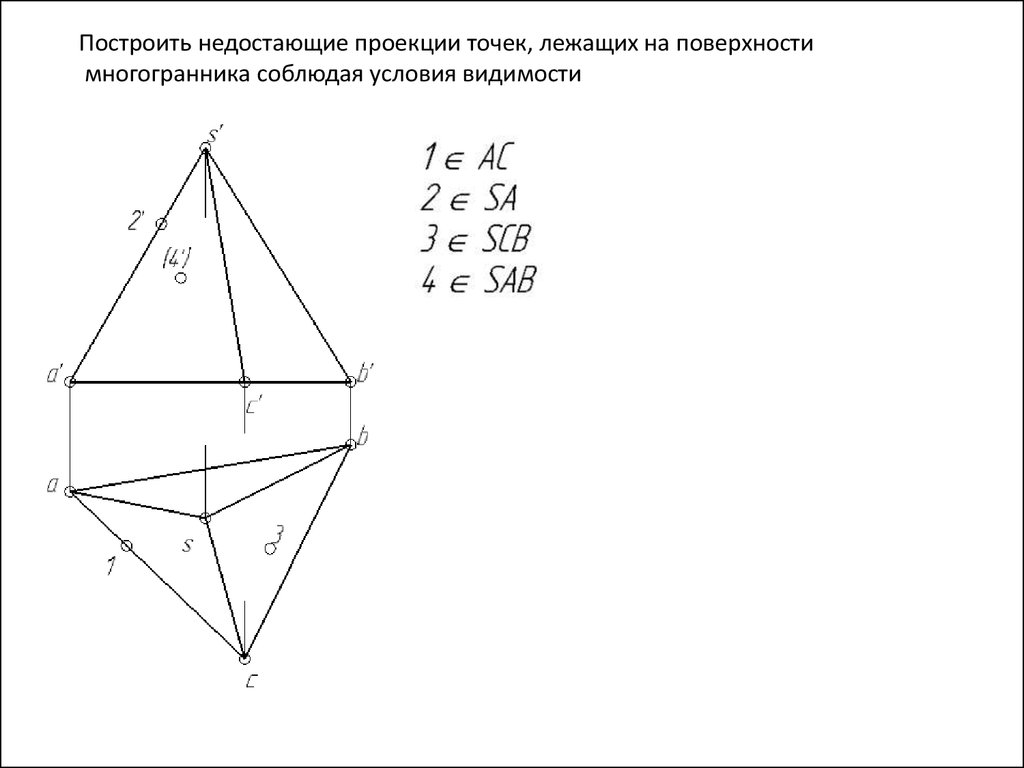
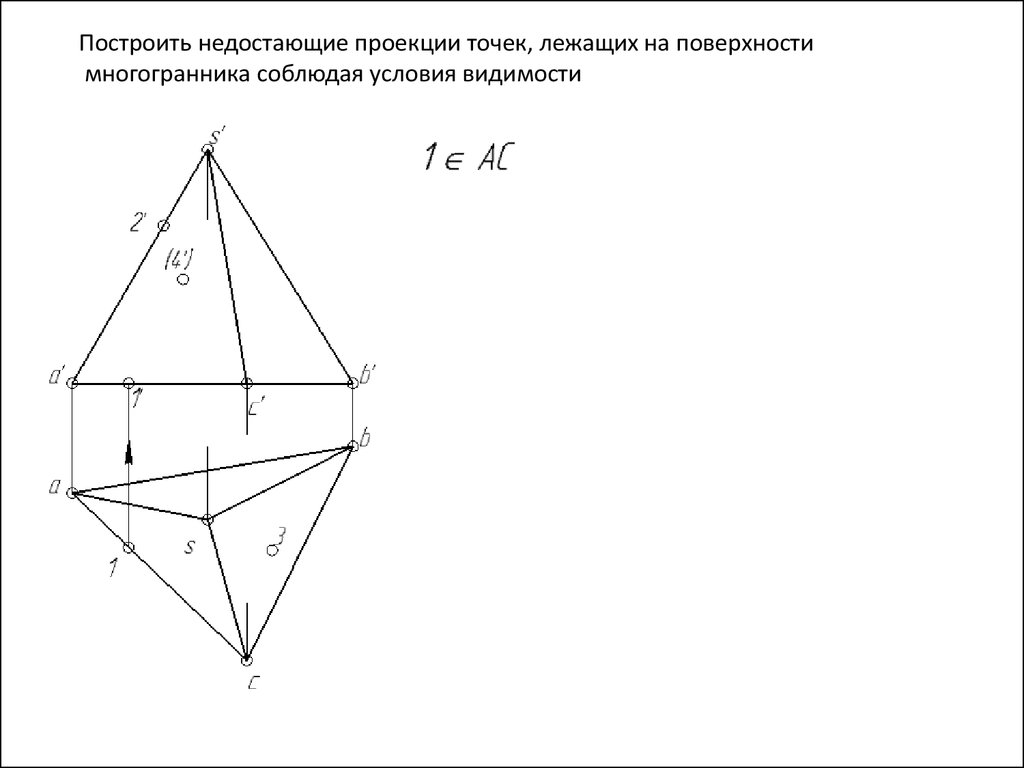
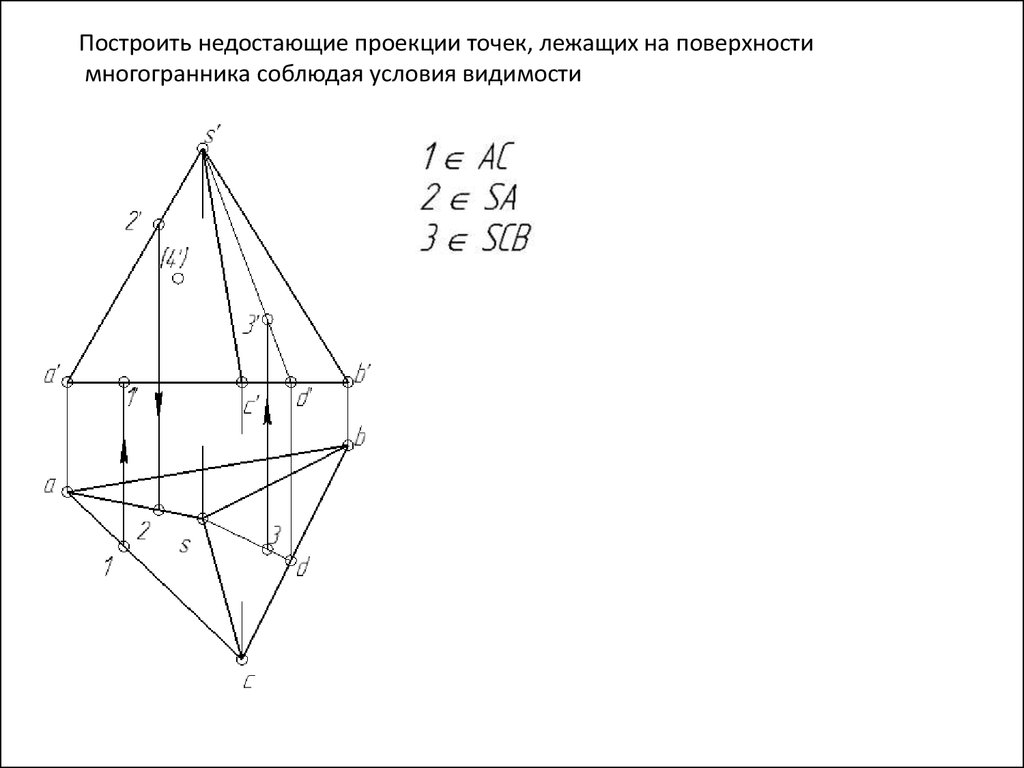
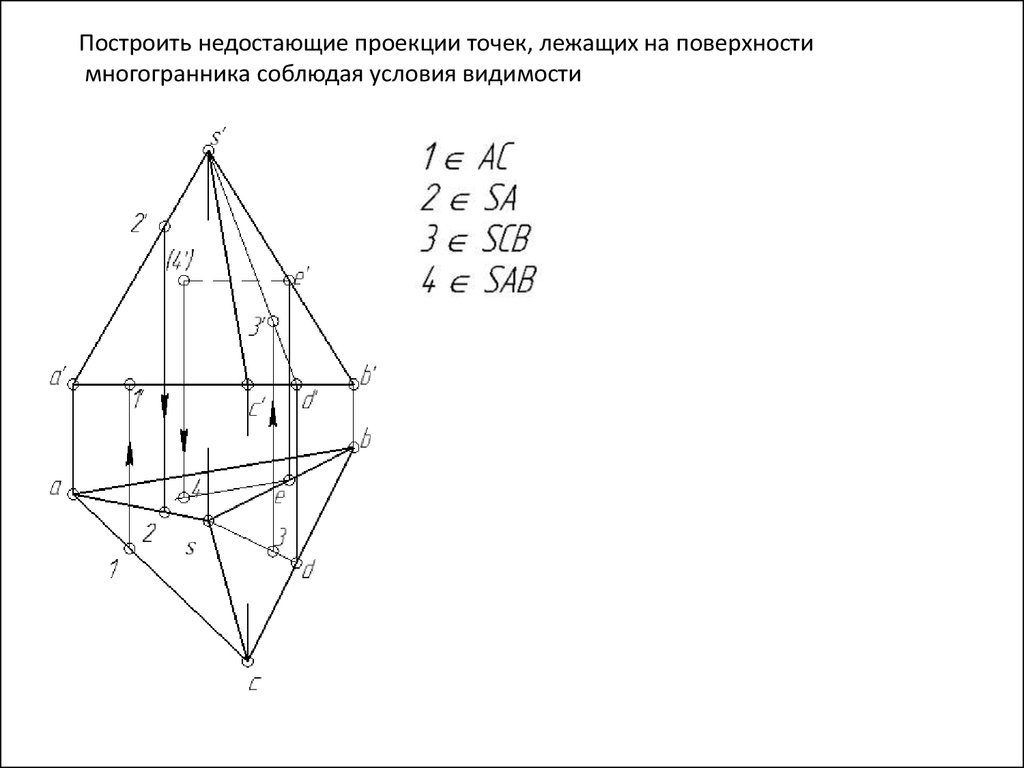
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
118.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
119.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
120.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
121.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
122.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
123.
Построить недостающие проекции точек, лежащих на поверхностимногогранника соблюдая условия видимости
124.
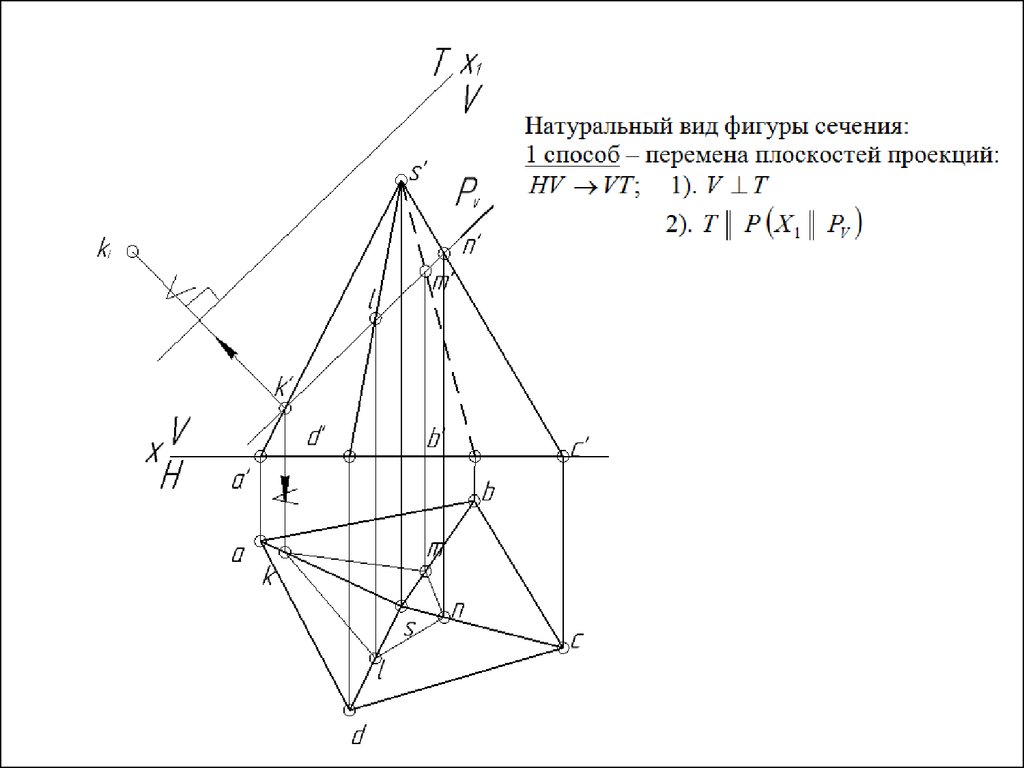
Пересечение многогранника проецирующей плоскостью.Натуральный вид фигуры сечения.
Сечение многогранника – геометрическая фигура в результате пересечения
многогранника плоскостью.
В общем случае плоскость пересекает многогранник по плоской фигуре многоугольнику, вид которого зависит от числа граней, пересекаемых плоскостью.
Два способа построения сечения многогранника плоскостью:
1). Способ ребер – по точкам пересечения ребер многогранника с плоскостью
(построение сводится к задаче на пересечение прямой с плоскостью).
2). Способ граней – по отрезкам прямых пересечения граней многогранника с
плоскостью (построение сводится к задаче на пересечение плоскостей).
125.
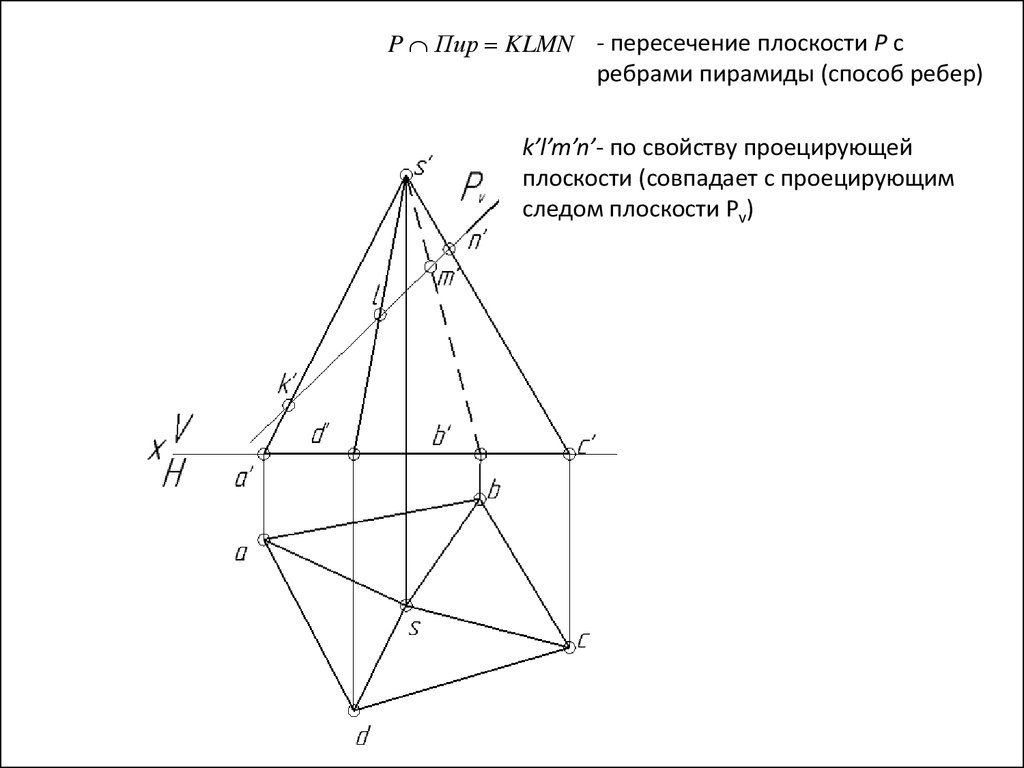
P Пир KLMN - пересечение плоскости Р сребрами пирамиды (способ ребер)
126.
P Пир KLMN - пересечение плоскости Р сребрами пирамиды (способ ребер)
k’l’m’n’- по свойству проецирующей
плоскости (совпадает с проецирующим
следом плоскости Pv)
127.
P Пир KLMN - пересечение плоскости Р сребрами пирамиды (способ ребер)
k’l’m’n’- по свойству проецирующей
плоскости (совпадает с проецирующим
следом плоскости Pv)
klmn- по принадлежности точек
соответствующим ребрам пирамиды:
K SA
128.
129.
130.
131.
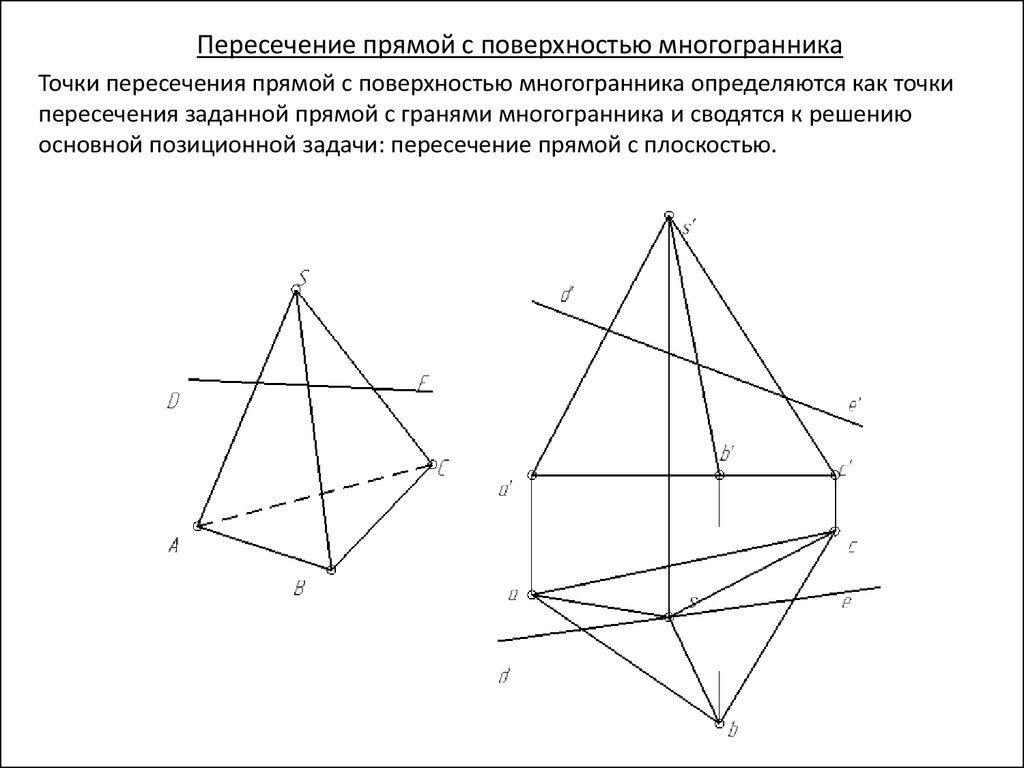
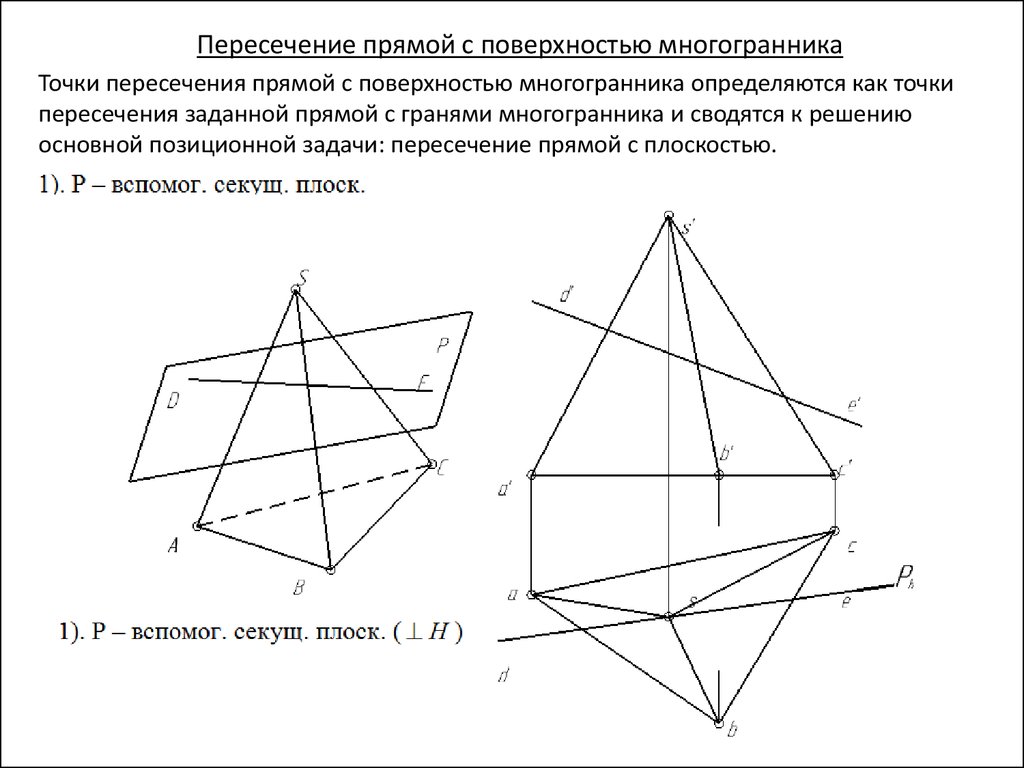
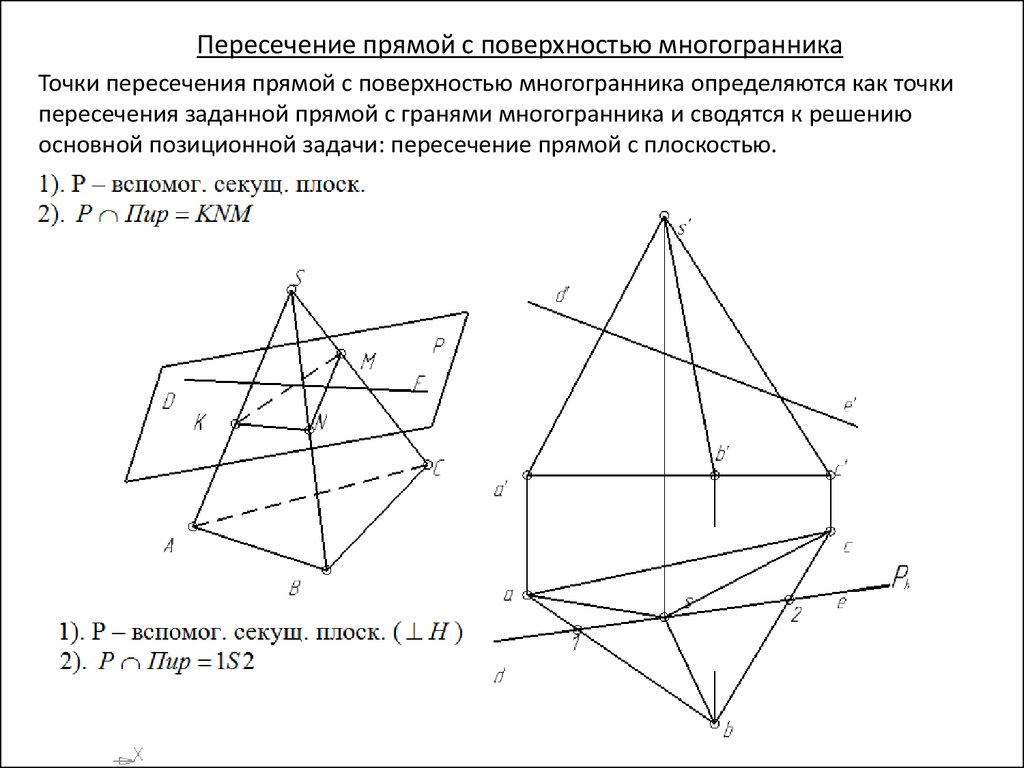
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
132.
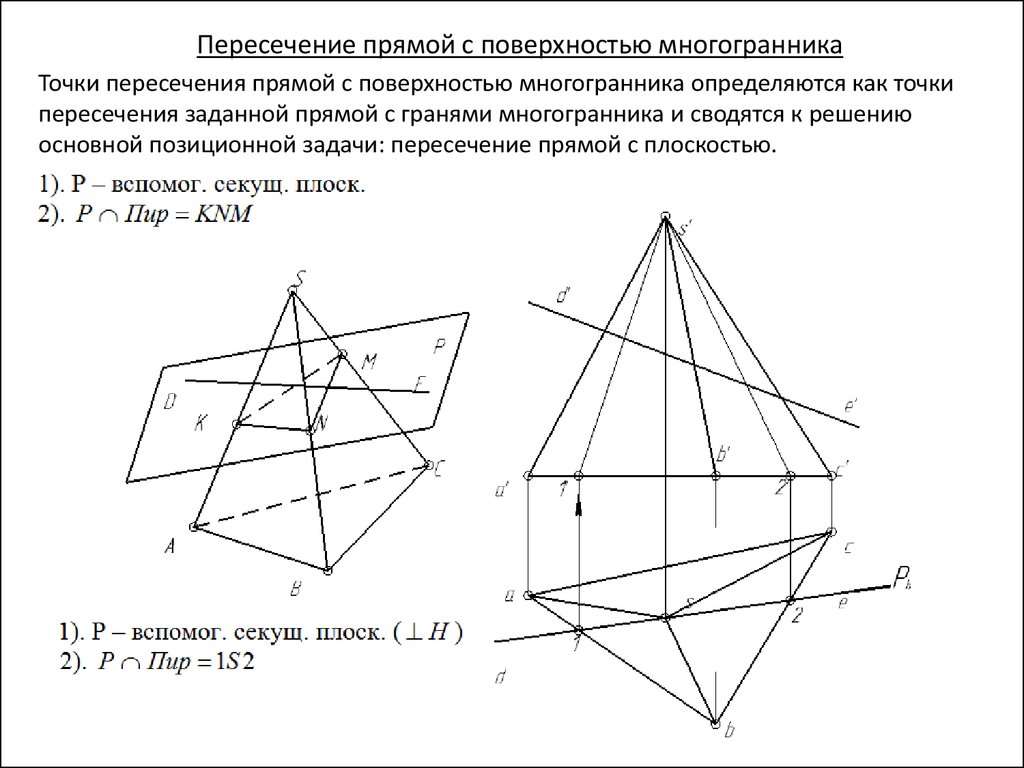
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
133.
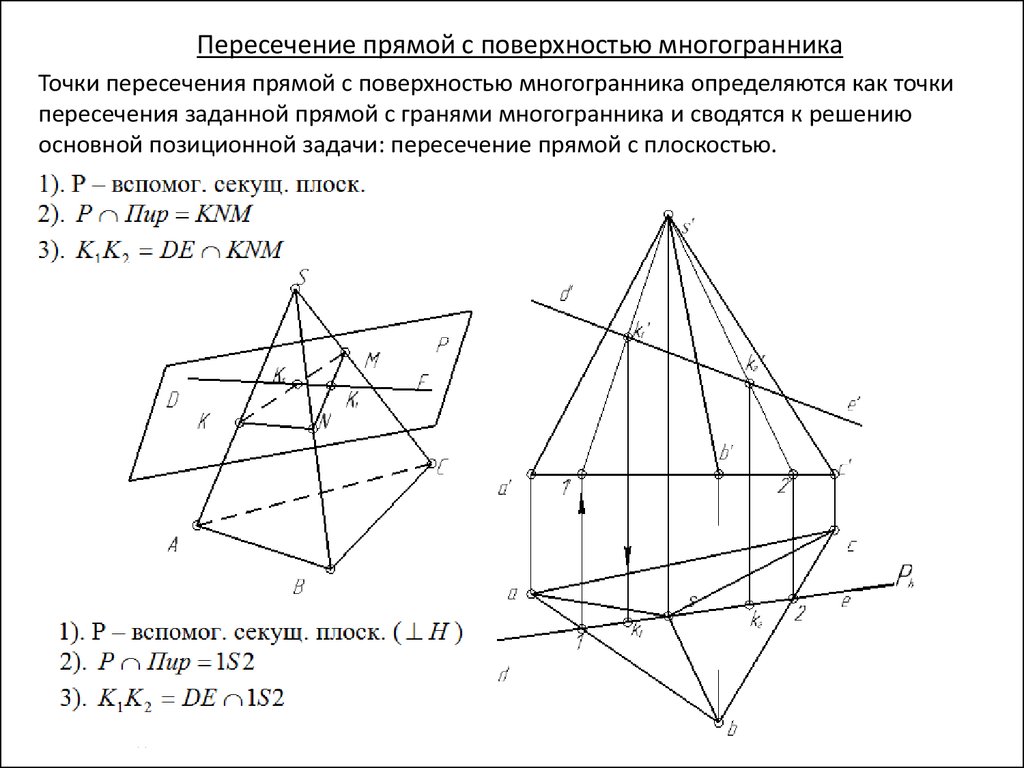
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
134.
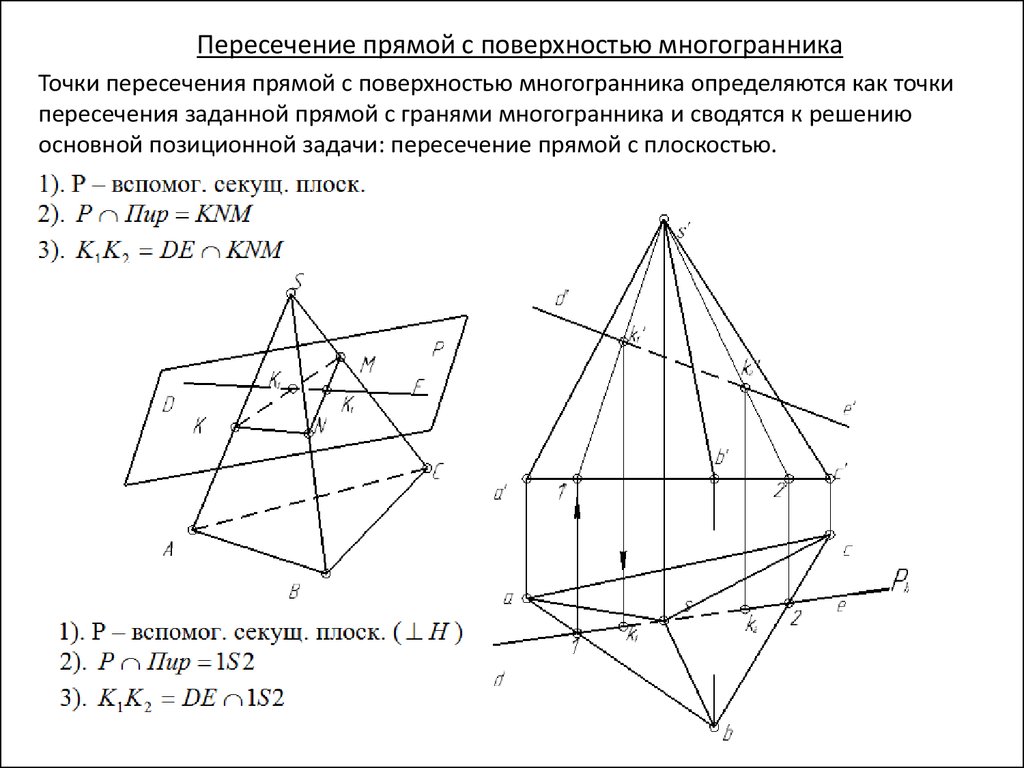
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
135.
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
136.
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
137.
Пересечение прямой с поверхностью многогранникаТочки пересечения прямой с поверхностью многогранника определяются как точки
пересечения заданной прямой с гранями многогранника и сводятся к решению
основной позиционной задачи: пересечение прямой с плоскостью.
138.
Взаимное пересечение многогранниковЛинию взаимного пересечения двух многогранников можно построить двумя
способами:
1). Способ ребер – по точкам пересечения ребер первого многогранника с
гранями второго и ребер второго многогранника с гранями первого.
Через найденные точки в определенной последовательности проводят
ломанную линию – линию пересечения. При этом можно соединять прямыми линиями
лишь ту пару точек, которые принадлежат одной и той же грани как одного, так и
другого многогранника.
2). Способ граней – по отрезкам прямых, по которым грани одной поверхности
пересекаются с гранями другой.
139.
Пример:Построить пересечения поверхности
пирамиды с поверхностью призмы
140.
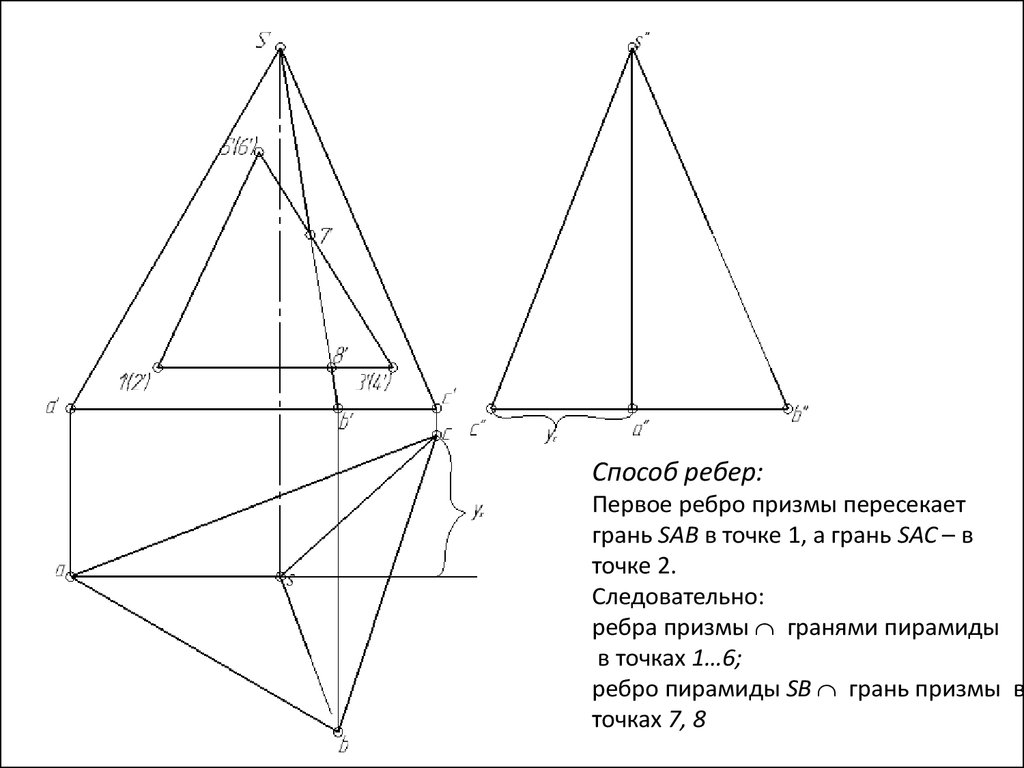
Способ ребер:Первое ребро призмы пересекает
грань SAB в точке 1, а грань SAC – в
точке 2.
Следовательно:
ребра призмы гранями пирамиды
в точках 1…6;
ребро пирамиды SB грань призмы в
точках 7, 8
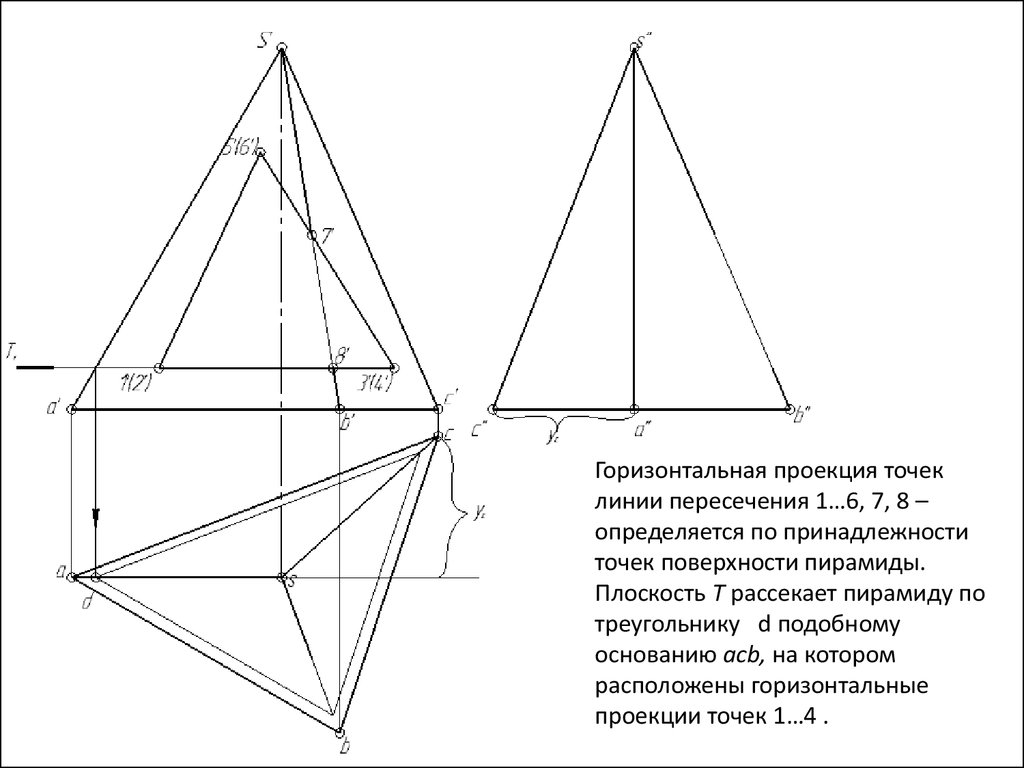
141.
Горизонтальная проекция точеклинии пересечения 1…6, 7, 8 –
определяется по принадлежности
точек поверхности пирамиды.
Плоскость Т рассекает пирамиду по
треугольнику d подобному
основанию acb, на котором
расположены горизонтальные
проекции точек 1…4 .
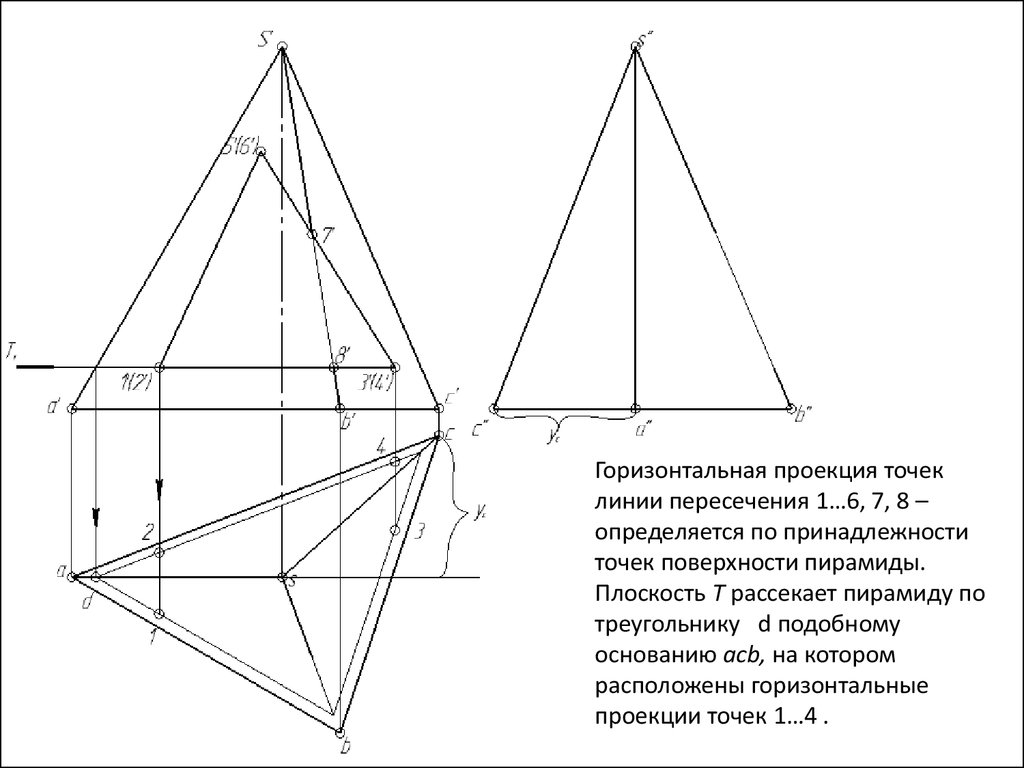
142.
Горизонтальная проекция точеклинии пересечения 1…6, 7, 8 –
определяется по принадлежности
точек поверхности пирамиды.
Плоскость Т рассекает пирамиду по
треугольнику d подобному
основанию acb, на котором
расположены горизонтальные
проекции точек 1…4 .
143.
Горизонтальная проекция точеклинии пересечения 1…6, 7, 8 –
определяется по принадлежности
точек поверхности пирамиды.
Плоскость Т рассекает пирамиду по
треугольнику d подобному
основанию acb, на котором
расположены горизонтальные
проекции точек 1…4 .
144.
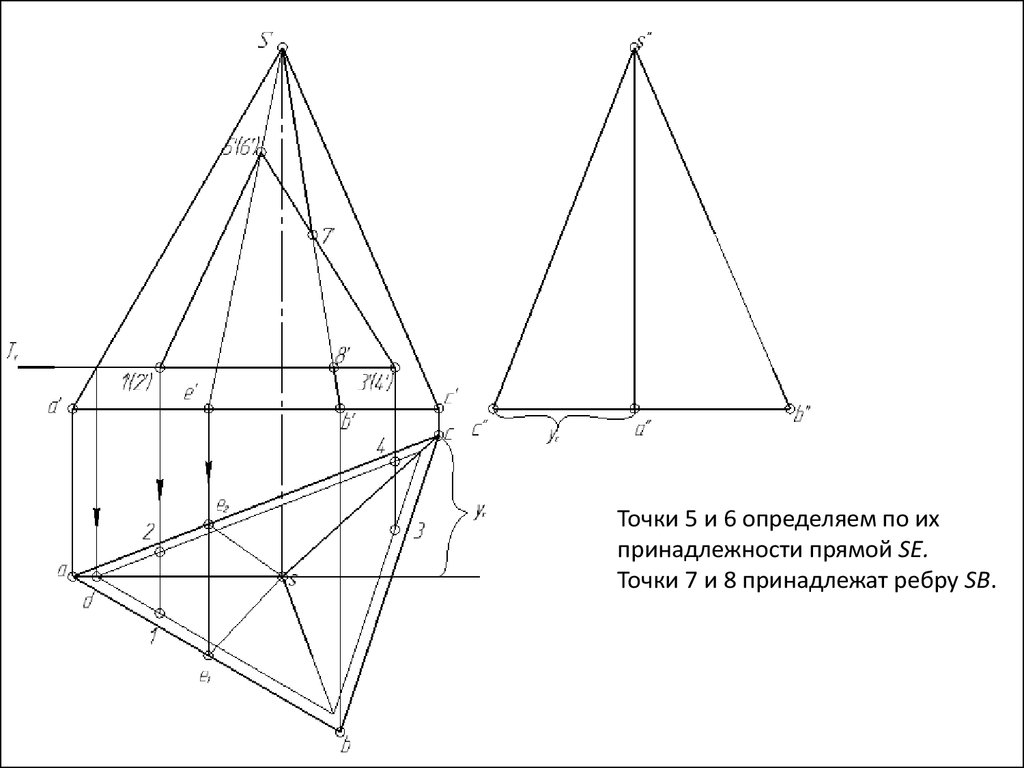
Точки 5 и 6 определяем по ихпринадлежности прямой SE.
Точки 7 и 8 принадлежат ребру SB.
145.
Точки 5 и 6 определяем по ихпринадлежности прямой SE.
146.
Точки 5 и 6 определяем по ихпринадлежности прямой SE.
Точки 7 и 8 принадлежат ребру SB.
147.
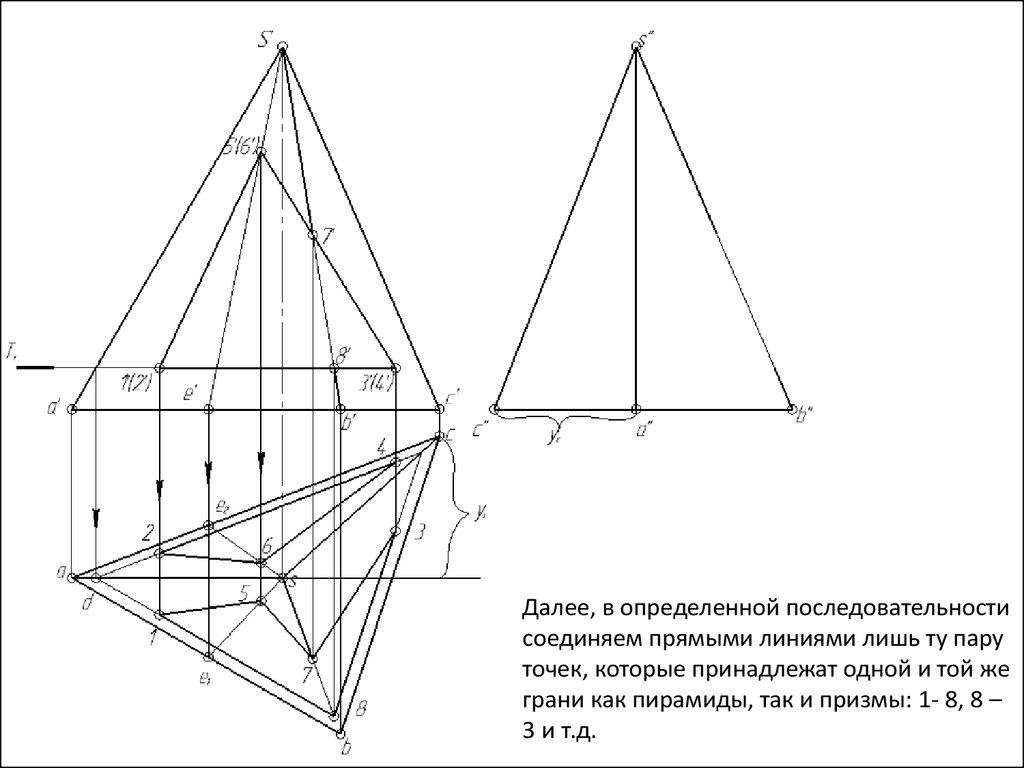
Далее, в определенной последовательностисоединяем прямыми линиями лишь ту пару
точек, которые принадлежат одной и той же
грани как пирамиды, так и призмы: 1- 8, 8 –
3 и т.д.
148.
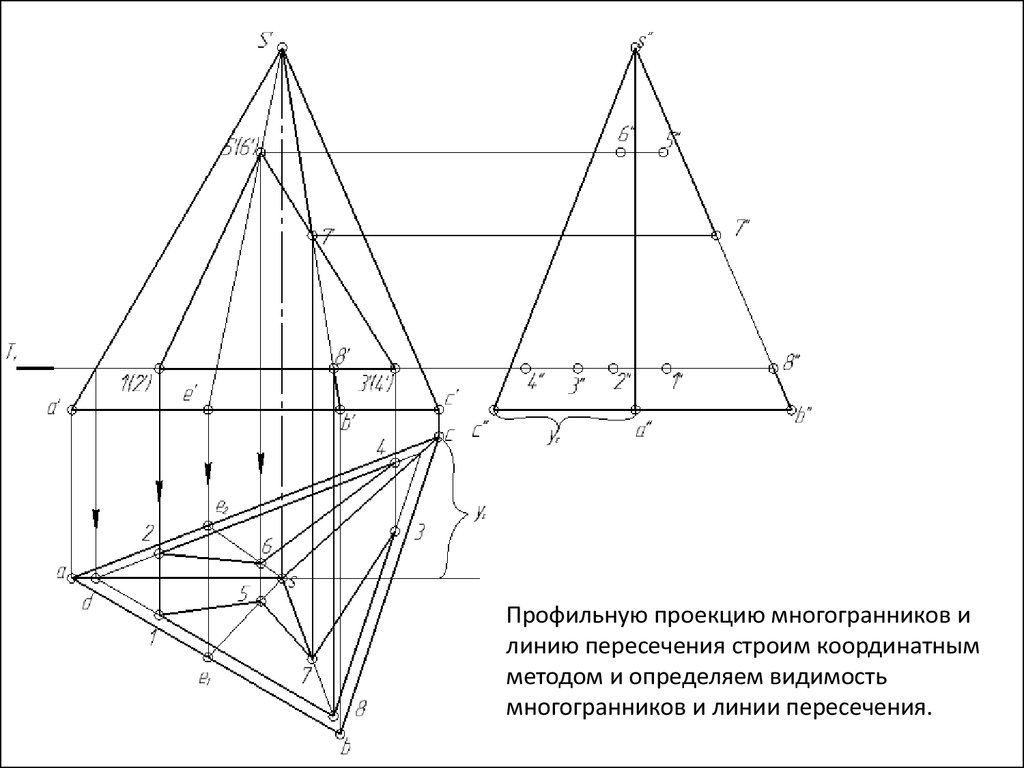
Профильную проекцию многогранников илинию пересечения строим координатным
методом и определяем видимость
многогранников и линии пересечения.
149.
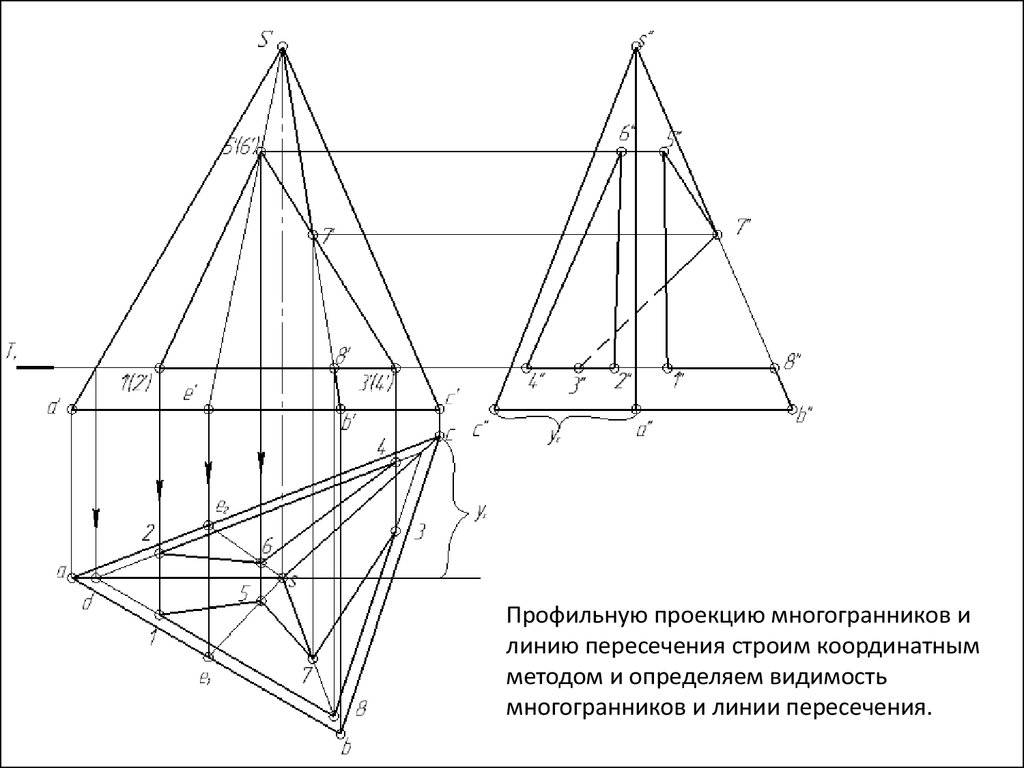
Профильную проекцию многогранников илинию пересечения строим координатным
методом и определяем видимость
многогранников и линии пересечения.
150.
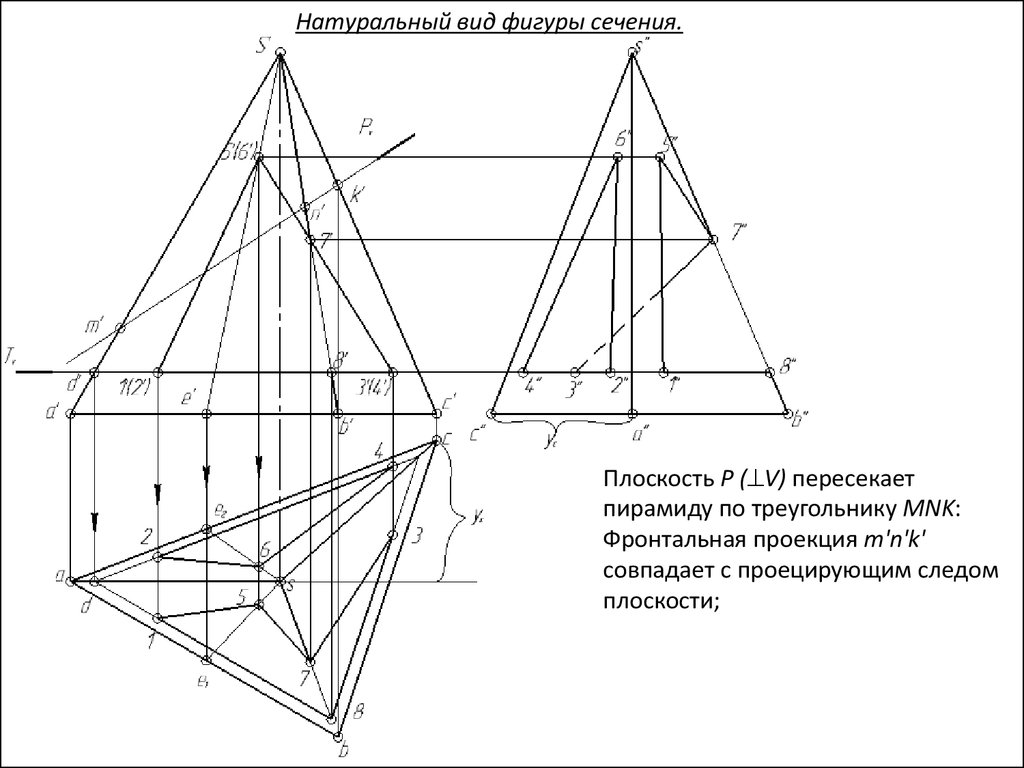
Натуральный вид фигуры сечения.Плоскость Р ( V) пересекает
пирамиду по треугольнику MNK:
Фронтальная проекция m'n'k'
совпадает с проецирующим следом
плоскости;
151.
Натуральный вид фигуры сечения.Плоскость Р ( V) пересекает
пирамиду по треугольнику MNK:
Фронтальная проекция m'n'k'
совпадает с проецирующим следом
плоскости;
горизонтальная проекция mnk
определяется по принадлежности
точек соответствующим ребрам.
152.
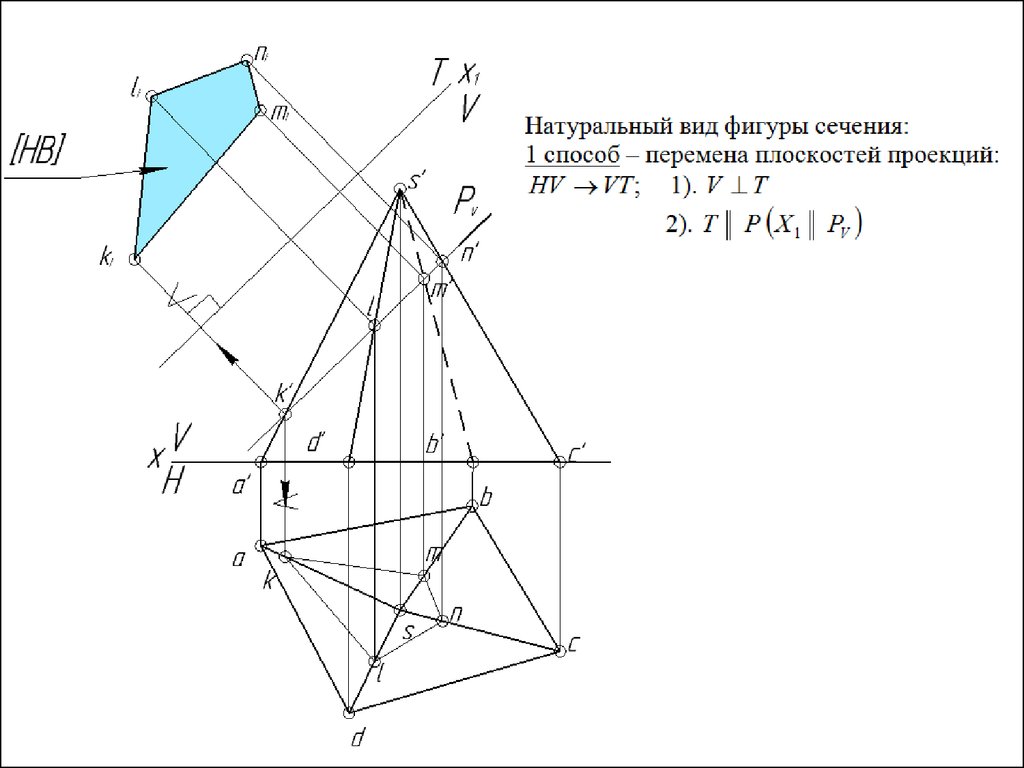
Натуральный вид фигуры сечения.Натуральный вид фигуры сечения
многогранников плоскостью Р строим
координатным методом:
в плоскости Р определяемся
системой координат Xp , Yp и к ней
относим фигуру сечения.
Координату Xp направляем по следу
Pv (Xp = xp') параллельно плоскости V ,
а координату Yp - перпендикулярно
плоскости V: Y (Yp = yp')
153.
Натуральный вид фигуры сечения.Натуральные величины
точек фигуры сечения по
координате Xp берем с
фронтальной проекции,
а по координате Yp –
с горизонтальной
проекции.
154.
Натуральный вид фигуры сечения.Натуральные величины
точек фигуры сечения по
координате Xp берем с
фронтальной проекции,
а по координате Yp –
с горизонтальной
проекции.
155.
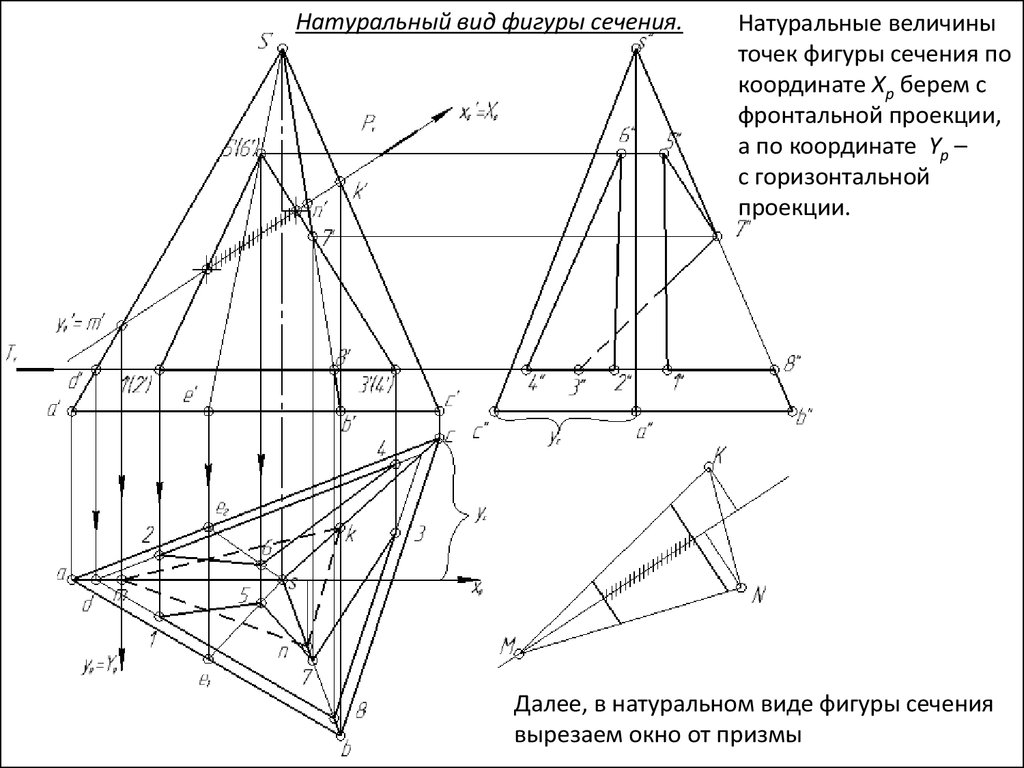
Натуральный вид фигуры сечения.Натуральные величины
точек фигуры сечения по
координате Xp берем с
фронтальной проекции,
а по координате Yp –
с горизонтальной
проекции.
Далее, в натуральном виде фигуры сечения
вырезаем окно от призмы
156.
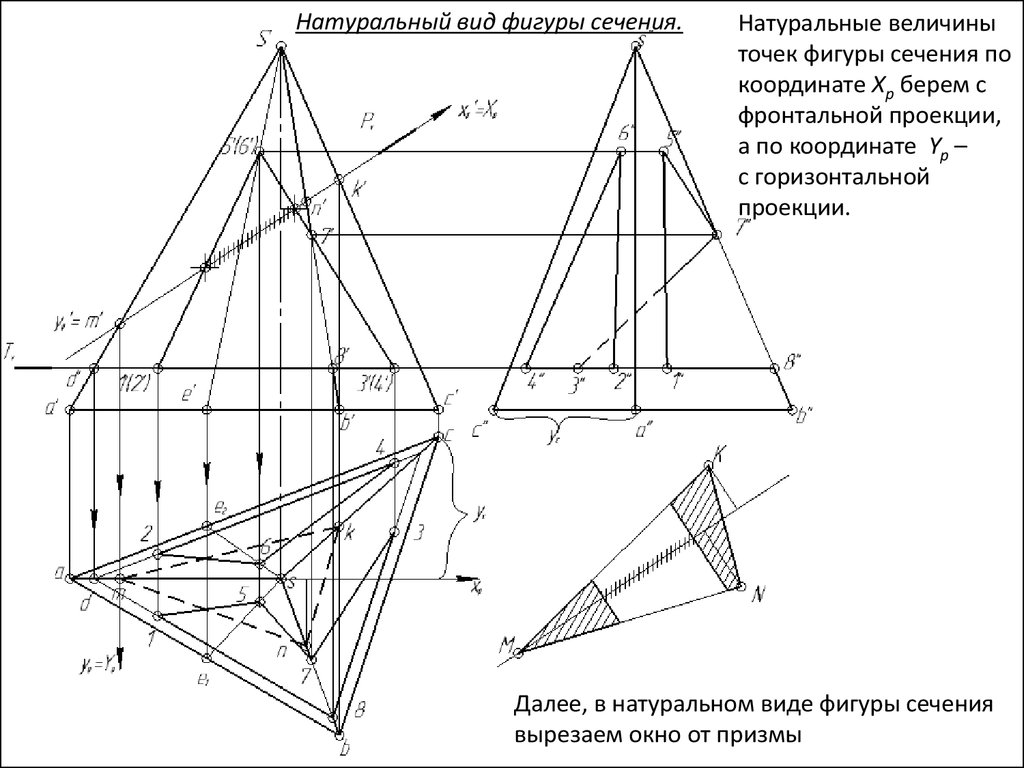
Натуральный вид фигуры сечения.Натуральные величины
точек фигуры сечения по
координате Xp берем с
фронтальной проекции,
а по координате Yp –
с горизонтальной
проекции.
Далее, в натуральном виде фигуры сечения
вырезаем окно от призмы




















































































 Инженерная графика
Инженерная графика








