Похожие презентации:
Тригонометрические функции, их свойства и графики
1.
Тригонометрическиефункции,
их свойства и графики
2.
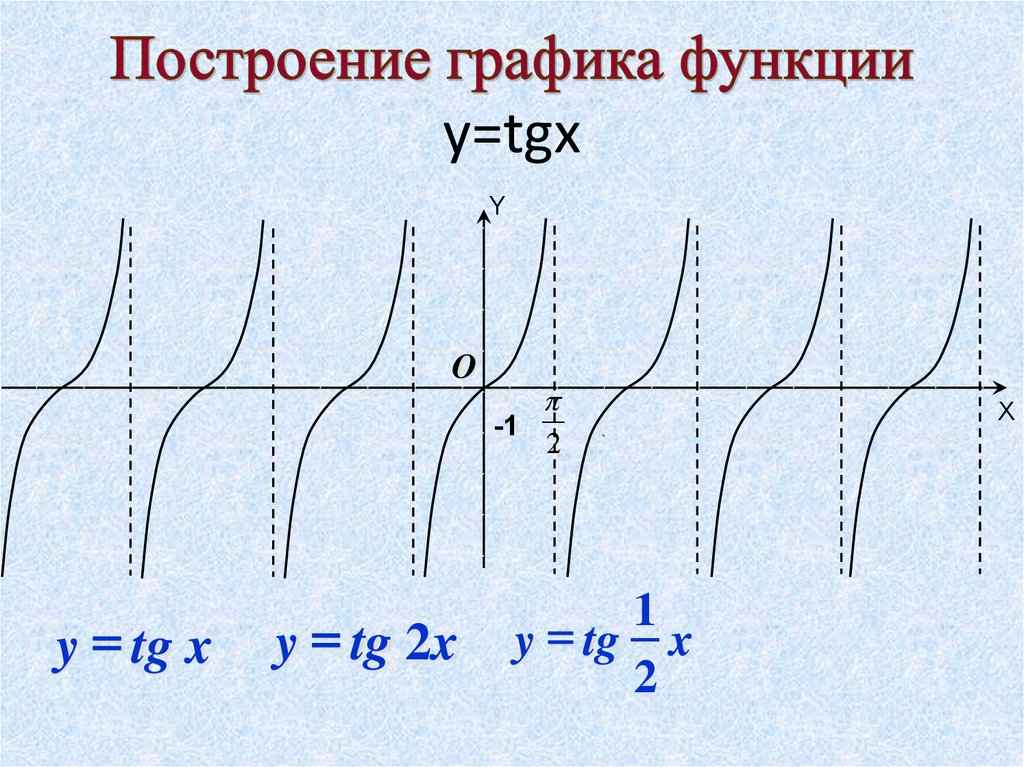
y=tgxY
O
-1
y = tg x
y = tg 2x
2
1
y = tg x
2
X
3.
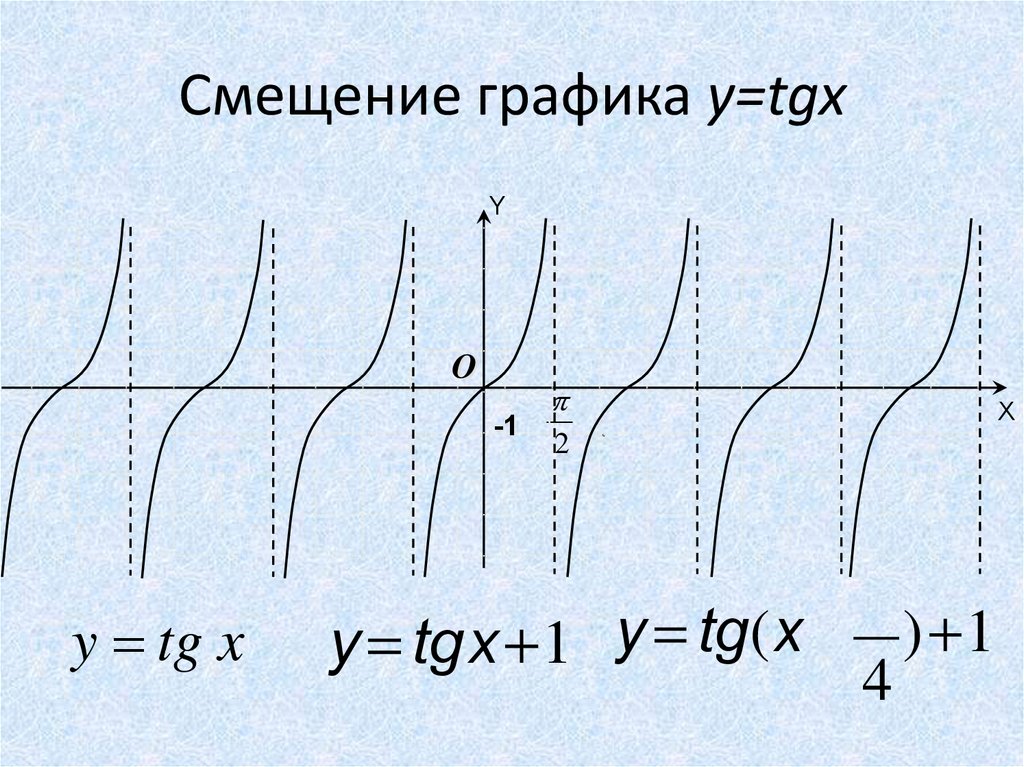
Смещение графика y=tgxY
O
-1
y = tg x
X
2
p
y = tgx+1 y = tg(x - ) +1
4
4.
Свойства графика функции y=tg x1. Область определения: x≠π/2+πn, n∈Z
2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая Т=π
Функция нечетная
y=0, при x=πn, n∈Z
y>0, при x∈(πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; πn), n∈Z
Функция возрастает на интервалах: (-π/2+πn; π/2+πn), n∈Z
5.
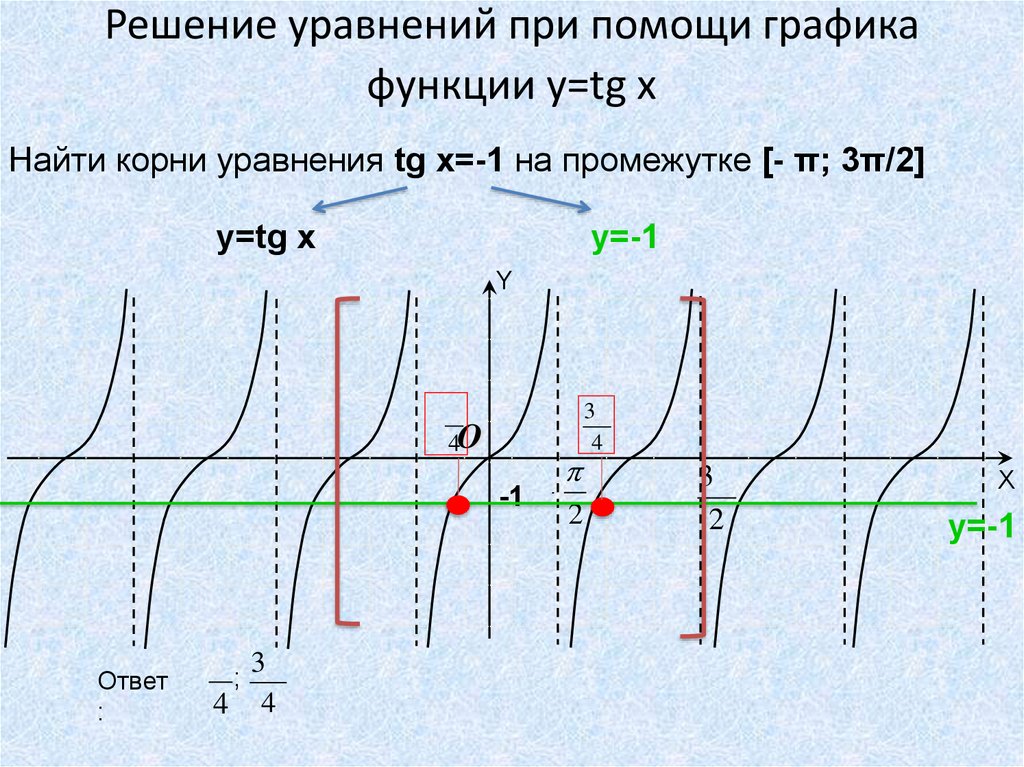
Решение уравнений при помощи графикафункции y=tg x
Найти корни уравнения tg x=-1 на промежутке [- π; 3π/2]
y=tg x
y=-1
Y
-
-p
p
3p
;
Ответ
4 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1
6.
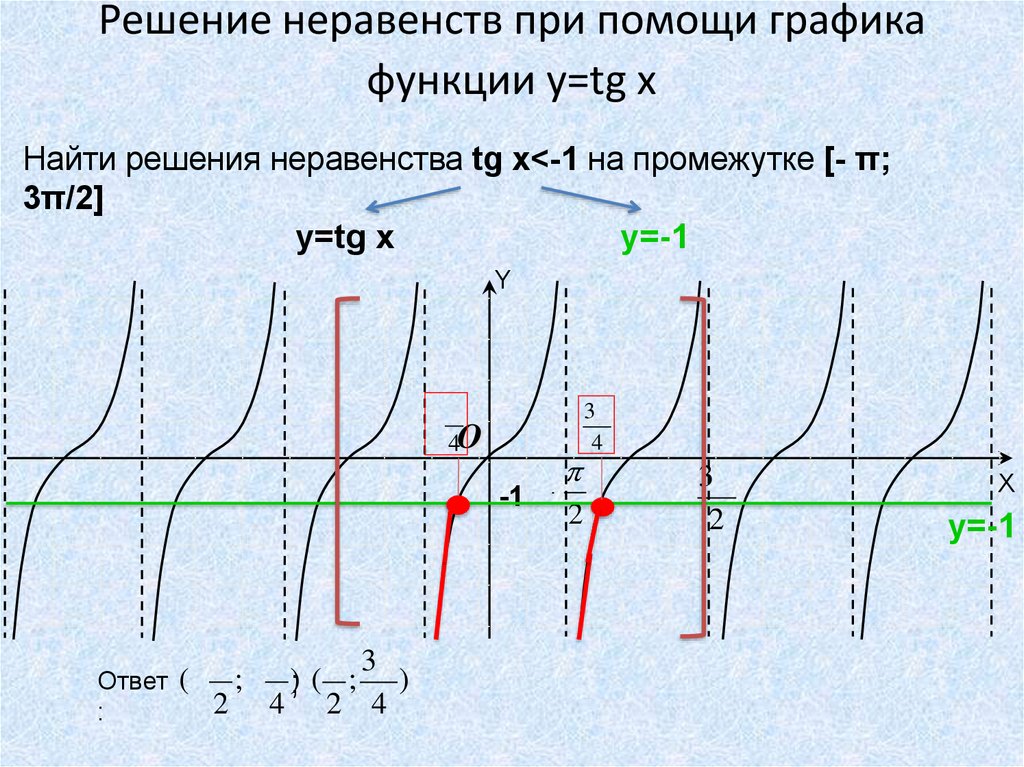
Решение неравенств при помощи графикафункции y=tg x
Найти решения неравенства tg x<-1 на промежутке [- π;
3π/2]
y=tg x
y=-1
Y
-
-p
p p p 3p
(;- ); ( ; )
Ответ
2 4 2 4
:
p
4O
-1
2
3p
4
3p
2
X
y=-1
7.
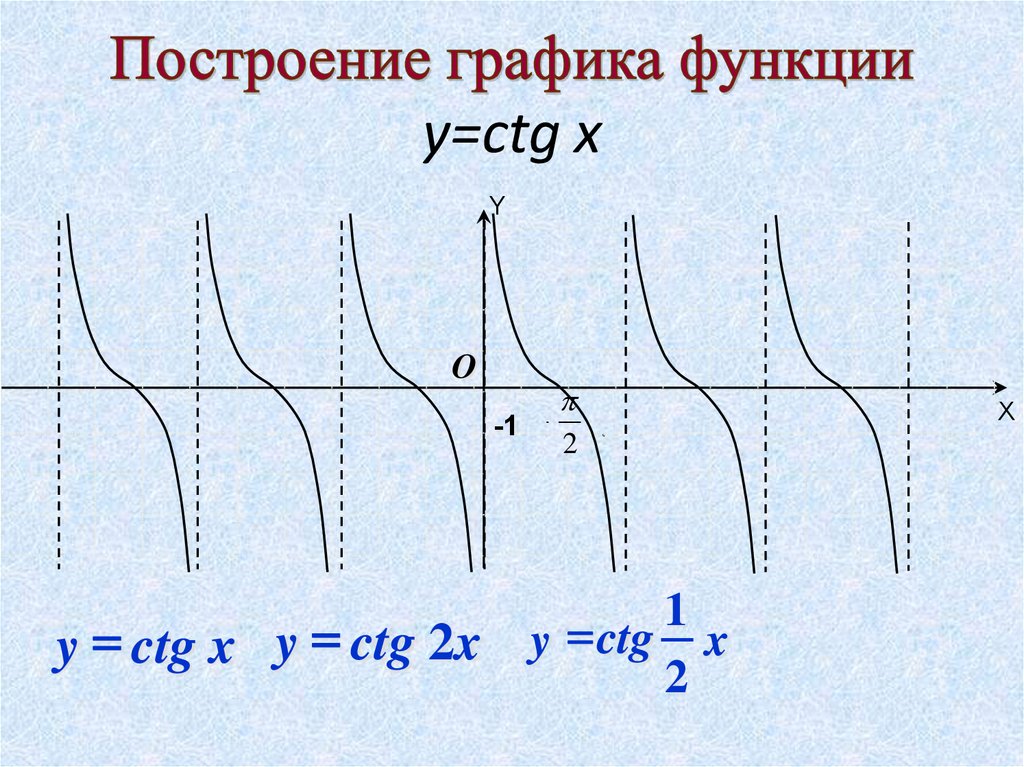
y=ctg xY
O
-1
y = ctg x y = ctg 2x
2
1
y = ctg x
2
X
8.
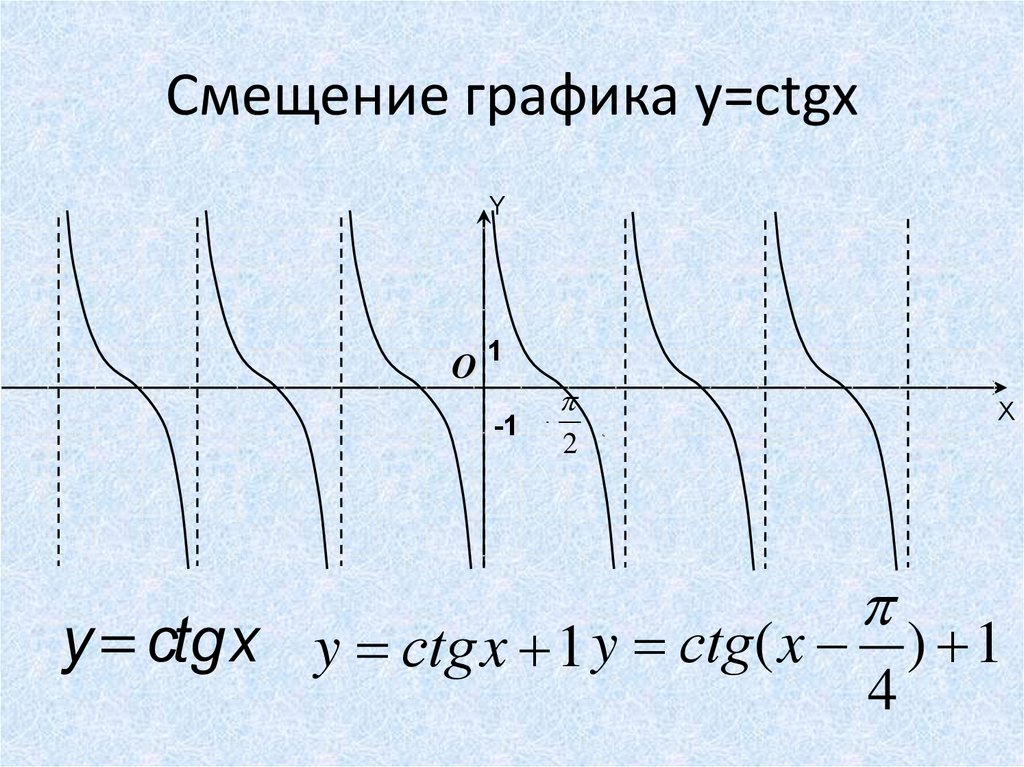
Смещение графика y=ctgxY
O1
-1
X
2
y = ctgx y = сtg x 1 y = сtg( x ) 1
4
9.
Свойства графика функции y=ctgx
1. Область определения: x≠πn, n∈Z
2. Множество значений: y∈(-∞;∞)
3.
4.
5.
6.
7.
8.
Функция периодическая T=π
Функция нечетная
y=0, при x=π/2+πn, n∈Z
y>0, при x∈(0+πn; π/2+πn), n∈Z
y<0, при x∈(-π/2+πn; 0+πn), n∈Z
Функция убывает на интервалах (πn; π+πn), n∈Z



 Математика
Математика