Похожие презентации:
Кёнигсбергские мосты
1. Кёнигсбергские мосты
Суриков Артём 8АБорисов Виктор
8А
2. Что это?
Кенигсбергские мосты - историческиизвестная математическая
задача. Его отрицательное
разрешение Леонардом Эйлером в 1736 году
заложило основы теории графов и
предвосхитило идею топологии.
Леонард
Кенигсбергские мосты
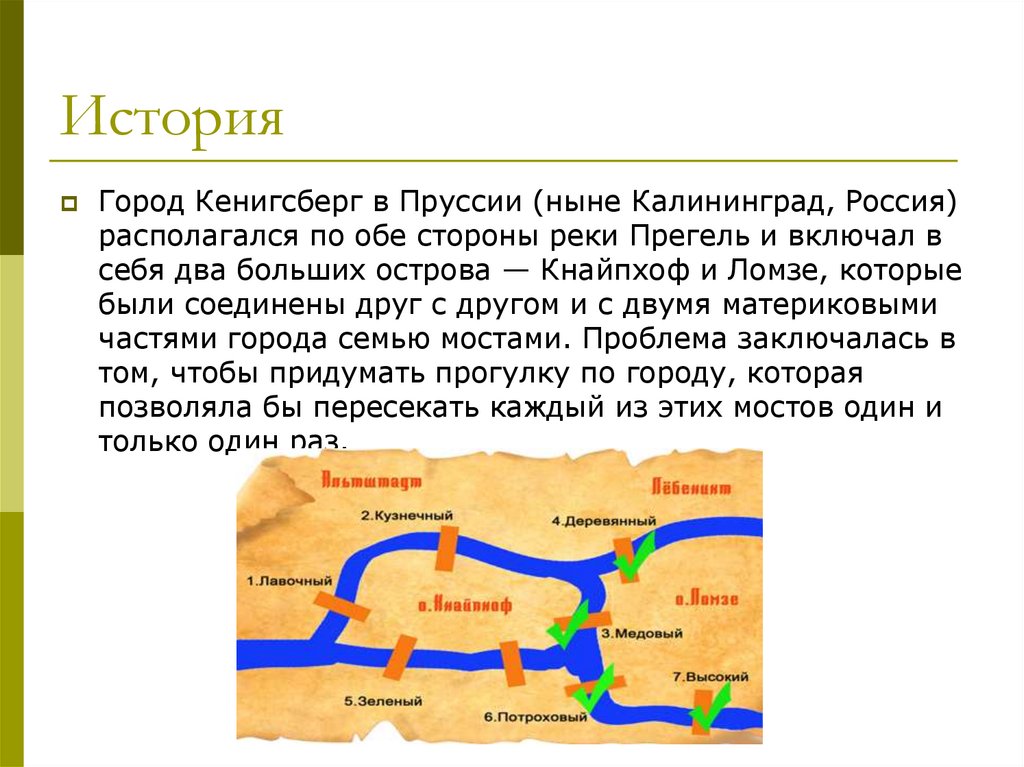
3. История
Город Кенигсберг в Пруссии (ныне Калининград, Россия)располагался по обе стороны реки Прегель и включал в
себя два больших острова — Кнайпхоф и Ломзе, которые
были соединены друг с другом и с двумя материковыми
частями города семью мостами. Проблема заключалась в
том, чтобы придумать прогулку по городу, которая
позволяла бы пересекать каждый из этих мостов один и
только один раз.
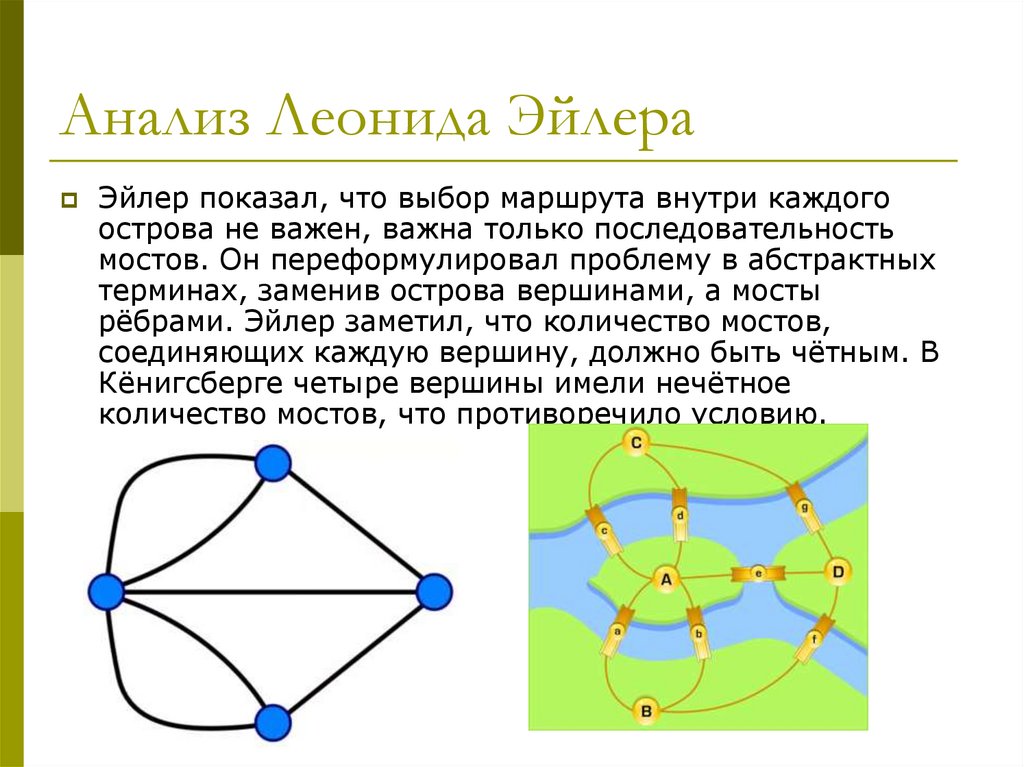
4. Анализ Леонида Эйлера
Эйлер показал, что выбор маршрута внутри каждогоострова не важен, важна только последовательность
мостов. Он переформулировал проблему в абстрактных
терминах, заменив острова вершинами, а мосты
рёбрами. Эйлер заметил, что количество мостов,
соединяющих каждую вершину, должно быть чётным. В
Кёнигсберге четыре вершины имели нечётное
количество мостов, что противоречило условию.
5. Значение в истории
Решение Эйлера считается первой теоремойтеории графов и первым истинным
доказательством в теории сетей.
Эйлер предвосхитил развитие топологии,
показав, что ключевая информация — это
количество мостов и их конечные точки.
Его доказательство поставило под сомнение
традиционное представление о математике как
науке о количестве.