Похожие презентации:
Алгоритмы на графах
1.
Алгоритмы на графахПрактика 8 неделя
2.
ЗАДАЧА О КРАТЧАЙШЕМ ПУТИНа языке графов это задача о самом коротком маршруте, то есть
поиске кратчайшего маршрута между точками графа или
минимизация суммарного весового показателя рёбер, из которых
состоит маршрут. Задача о самом коротком маршруте считается
самой важной основополагающей задачей теории графов.
В исходном (старом варианте) она звучит как задача о
коммивояжере. Важность этой задачи видна из её разных
практических реализаций. К примеру, в навигаторах, работающих
на основе GPS, выполняется нахождение маршрута минимальной
длины между двумя перекрёстками. Вершинами графа в этом
случае считаются перекрёстки, а рёбрами будут дороги,
соединяющие перекрёстки.
Когда суммарная длина пути между перекрёстками станет самой
маленькой, то это значит, что найден оптимальный путь движения.
3.
Постановка задачиПроблема нахождения самого короткого пути на графе
существует
для
случаев
ориентированного,
неориентированного и смешанного графов. Рассмотрим
постановку задачи в наиболее простом варианте для
неориентированного графа. При рассмотрении случая
ориентированного или смешанного графа, необходимо ещё
учесть в каких направлениях расположены рёбра графа.
Маршрут или путь внутри неориентированного графа
является последовательным набором вершин (точек).
Существует функция веса, отображающая рёбра с их весами,
и неориентированный граф. Тогда минимальным путём из
одной вершины в другую будет считаться путь, имеющий
минимальную сумму. В случае, когда у всех рёбер одинаковый
вес, тогда целью становится минимизация числа рёбер,
которые надо пройти по маршруту.
4.
Варианты постановокНахождение кратчайшего маршрута к заданному пункту
назначения. Необходимо сформировать самый короткий
путь к пункту назначения, вершине t. Начало пути может
быть в любой из вершин графа, кроме t. Если изменить
направление всех рёбер графа, то задача сводится к задаче
о единой начальной точке и в ней надо найти минимальный
путь из исходной точки во все остальные.
Нахождение минимального маршрута между определённой
парой точек. То есть необходимо определить самый короткий
путь из точки U в точку V.
Нахождение минимального маршрута между всеми парами
вершин. То есть надо определить самый короткий путь из
каждой точки U в каждую точку V. Такую задачу возможно
разрешить при помощи алгоритма, который предназначен
для задачи с одной начальной точкой, но есть возможность
решить её быстрее.
5.
Отрасли примененияВ разных постановочных вариантах, в качестве
веса ребра могут фигурировать не только меры
длины, но и цена, временные интервалы, ресурсы и
так далее. Или иные параметры, которые могут быть
связаны с преодолением всех рёбер пути.
Это
означает,
что
задача
может
быть
использована в самых разных научных сферах
(информатике, экономике, географии и других). Но
бывают случаи, когда при решении задачи о
минимальном маршруте, требуется учесть различные
ограничивающие факторы.
Так как есть много разных постановок этой задачи, то,
соответственно, существуют различные алгоритмы
нахождения самого короткого маршрута на графе.
6.
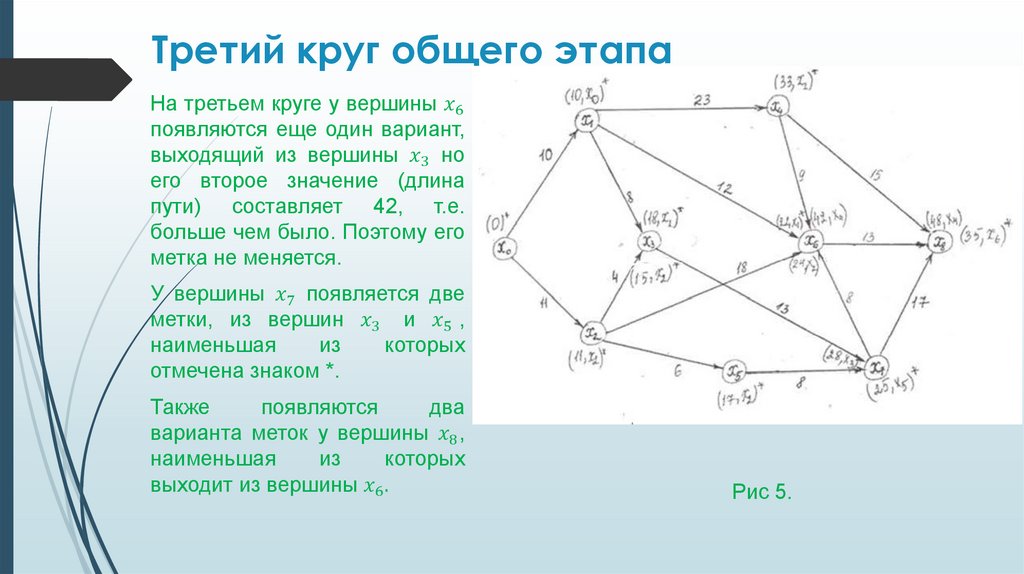
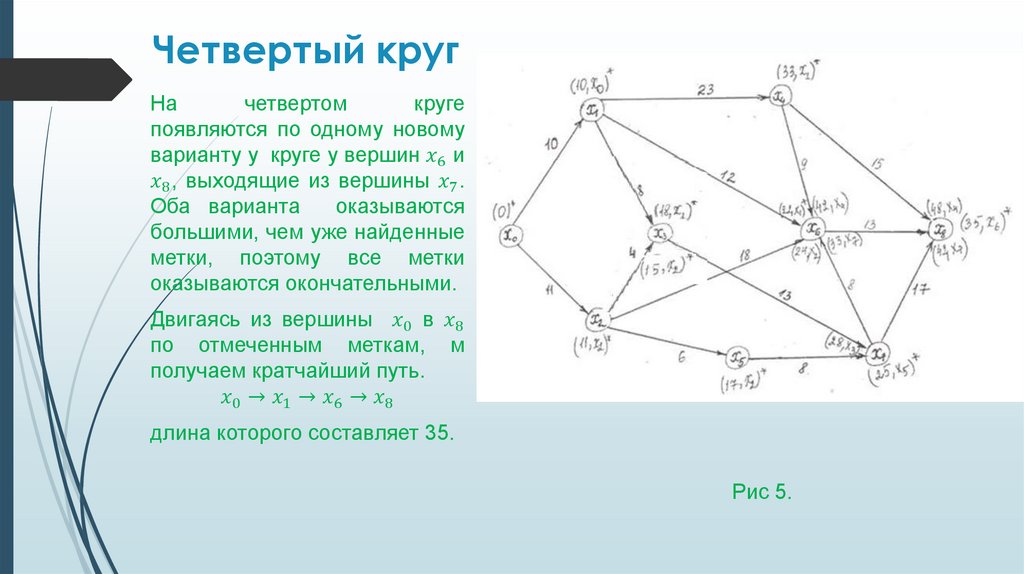
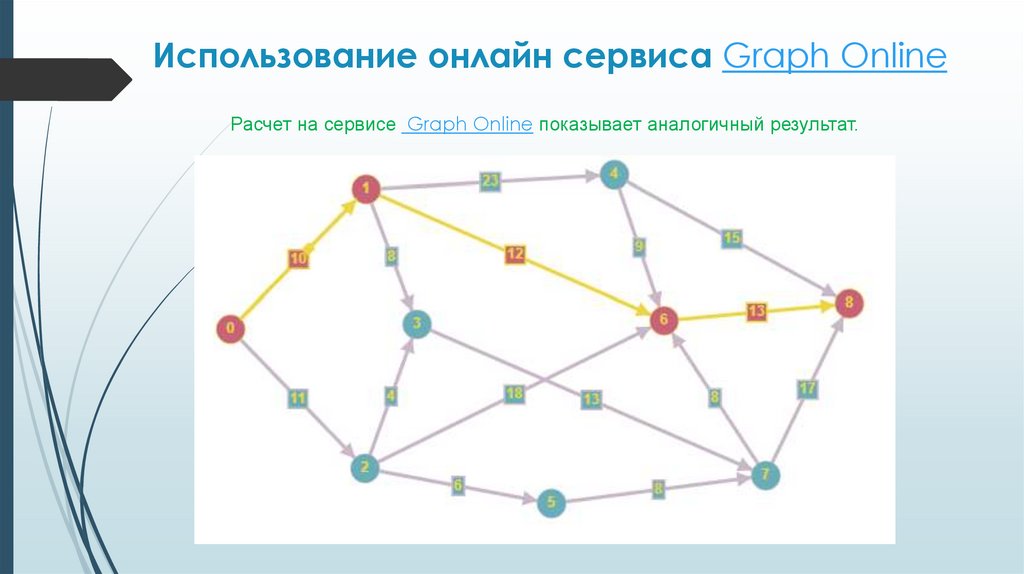
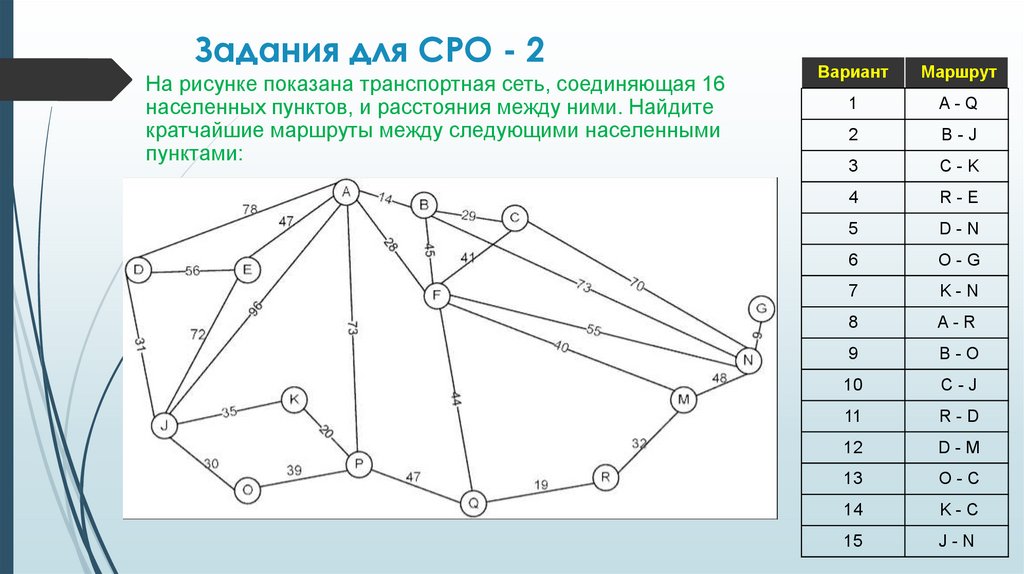
Алгоритм ФордаВ заданном графе рисунке 1 найти
кратчайшее расстояние с вершины





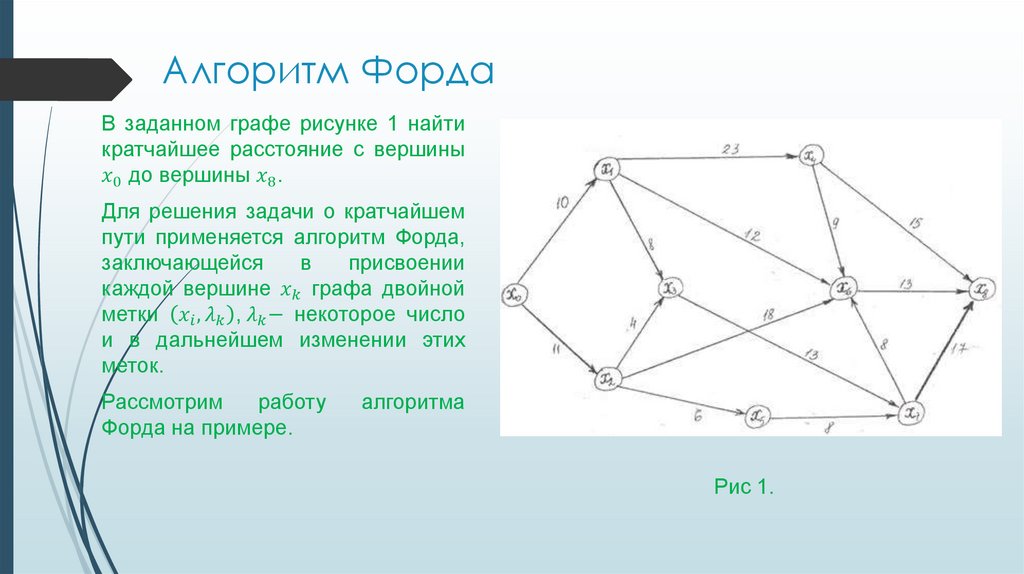
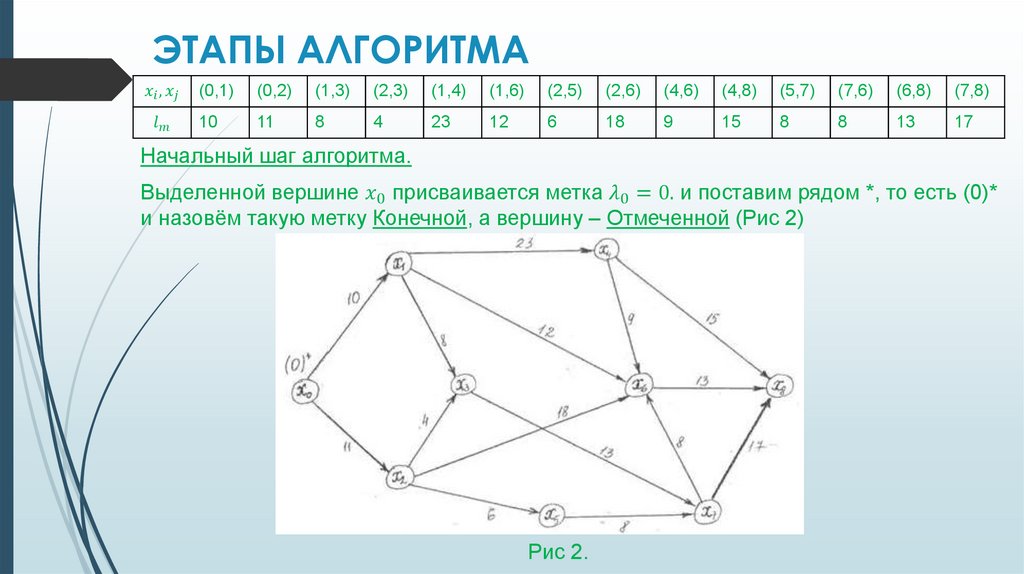
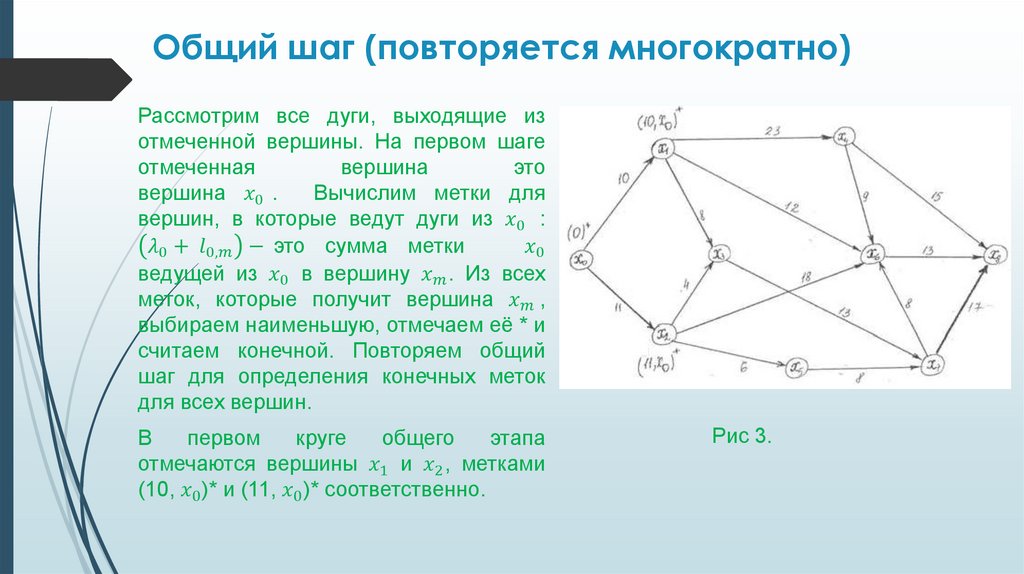
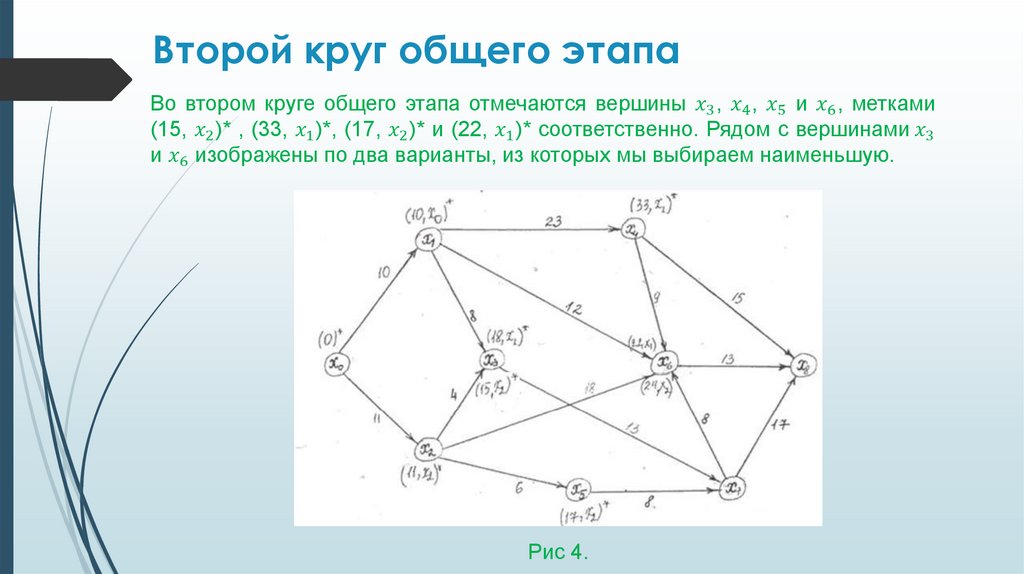
 Информатика
Информатика








