Произвольная система сил

1. Произвольная система сил

Занятие №3

2. Приведение системы сил к центру

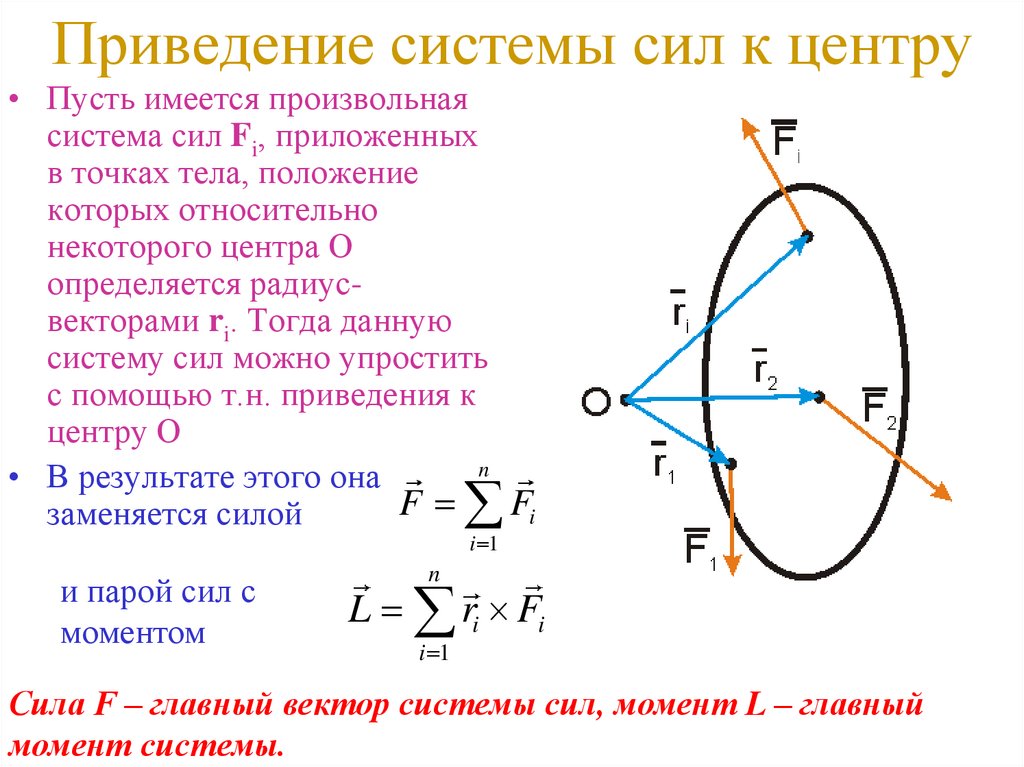
• Пусть имеется произвольная
система сил Fi, приложенных
в точках тела, положение
которых относительно
некоторого центра О
определяется радиусвекторами ri. Тогда данную
систему сил можно упростить
с помощью т.н. приведения к
центру О
n
• В результате этого она
F Fi
заменяется силой
i 1
и парой сил с
моментом
n
L ri Fi
i 1
Сила F – главный вектор системы сил, момент L – главный
момент системы.

3. Изменение центра приведения

• Главный вектор системы не изменится
• Он называется первым инвариантом системы сил
• Главный момент изменится
• Вторым инвариантом системы сил является скалярное
произведение главного вектора системы на ее главный
момент.
F L
Иногда в качестве второго инварианта берут проекцию
главного момента на направление главного вектора
L L cos L, F
*

4.

Главный момент L всегда можно разложить на две
составляющие, одна из которых направлена вдоль
главного вектора F, а другая – перпендикулярно ему.
Так как главный момент зависит от центра приведения,
а его продольная составляющая L* – нет, то,
следовательно, с переменой центра приведения будет
меняться только перпендикулярная составляющая L.
Можно найти такой центр приведения, для которого
перпендикулярная составляющая обратится в нуль, и
главный момент L будет коллинеарен главному вектору
F. Такая совокупность силы и момента называется
динамическим винтом или динамой. К динаме
приводится всякая система сил, для которой второй
инвариант не равен нулю.

5. Возможные результаты приведения (по второму инварианту)

• 1. L F 0. Система сил приводится к динаме.
• 2. L F = 0. Возможны частные результаты:
• a) F = 0, L 0. Система сил приводится к паре
сил с моментом L.
• b) F 0, L = 0 или L перпендикулярен F.
Система сил приводится к равнодействующей
величины F.
• c) F = 0, L = 0. Система сил находится в
равновесии.

6. Уравнения равновесия системы сил

• Условие равновесия произвольной системы сил
n
n
F 0; r F 0
i 1
i
i 1
i
i
• В общем случае в проекциях на оси координат из этих
двух векторных уравнений получается 6 скалярных
уравнений равновесия.
• В плоском случае условие для сил дает два скалярных
уравнения, а условие для моментов – одно, т.к. векторы
Li перпендикулярны плоскости, в которой лежат силы.
Уравнение для моментов сводится к алгебраической
сумме моментов сил (со своими знаками).

7. Условия равновесия плоской системы сил

n
n
n
X 0; Y 0; L 0
i 1
i
i 1
i
i 1
i
•Для равновесия произвольной плоской системы сил необходимо и
достаточно, чтобы сумма проекций всех сил на каждую из двух
координатных осей, произвольно взятых в плоскости действия сил,
равнялась нулю, и сумма моментов всех сил относительно любого
произвольно взятого в той же плоскости центра равнялась нулю.
•Для равновесия плоской системы сил необходимо и достаточно, чтобы
сумма моментов всех сил относительно каждого из трех произвольных,
но не лежащих на одной прямой, центров равнялась нулю (теорема о трех
моментах).
•Для равновесия плоской системы сил необходимо и достаточно, чтобы
сумма моментов всех сил относительно двух произвольных центров и
сумма проекций этих сил на произвольную ось, не перпендикулярную к
прямой, соединяющей эти центры, равнялась нулю.
Так как в плоском случае число уравнений равновесия равно трем, то
система сил будет статически определимой, если число неизвестных не
превысит трех.

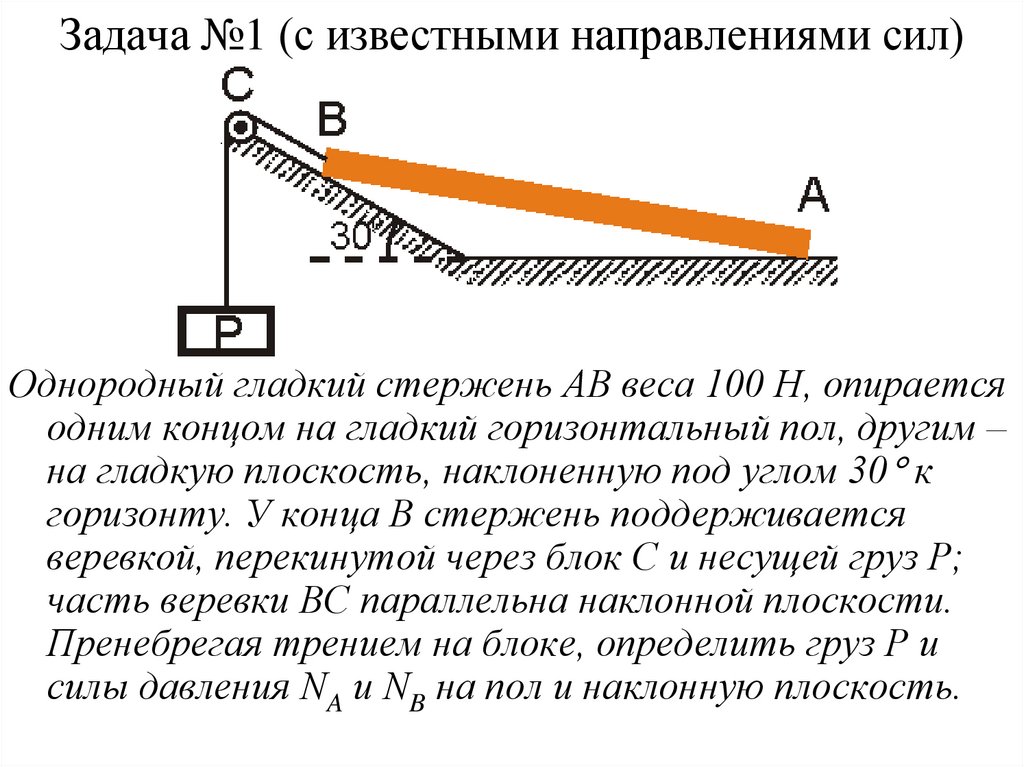
8. Задача №1 (с известными направлениями сил)

Однородный гладкий стержень АВ веса 100 Н, опирается
одним концом на гладкий горизонтальный пол, другим –
на гладкую плоскость, наклоненную под углом 30 к
горизонту. У конца В стержень поддерживается
веревкой, перекинутой через блок С и несущей груз Р;
часть веревки ВС параллельна наклонной плоскости.
Пренебрегая трением на блоке, определить груз Р и
силы давления NA и NB на пол и наклонную плоскость.

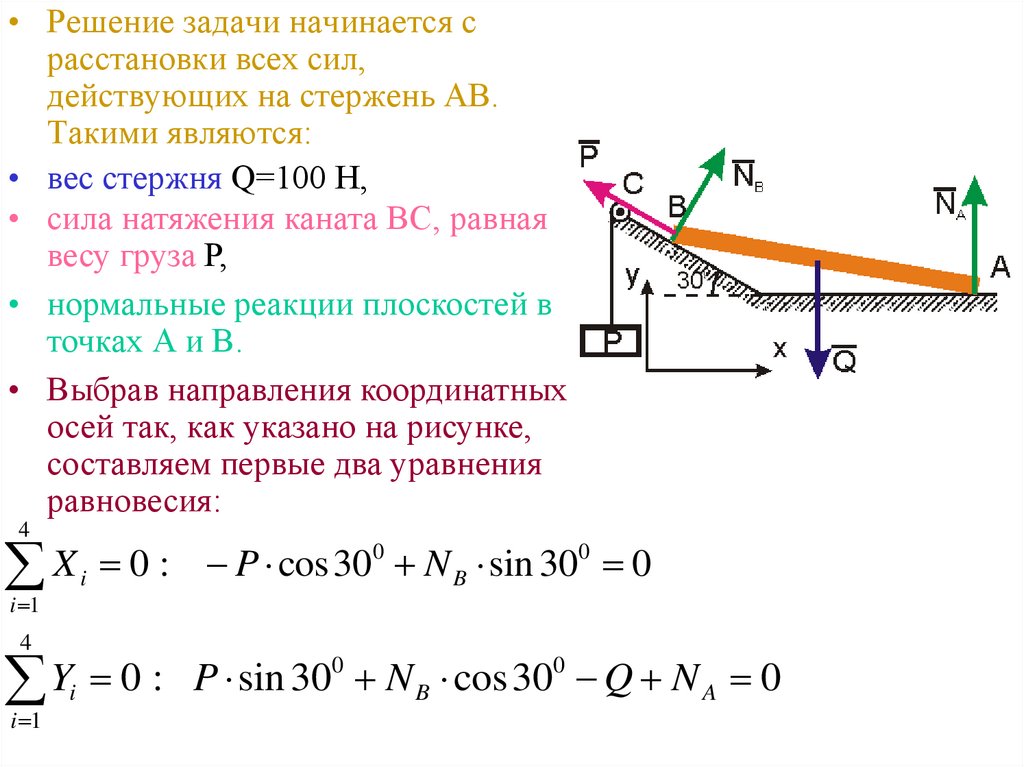
9.

• Решение задачи начинается с
расстановки всех сил,
действующих на стержень АВ.
Такими являются:
• вес стержня Q=100 Н,
• сила натяжения каната ВС, равная
весу груза Р,
• нормальные реакции плоскостей в
точках А и В.
• Выбрав направления координатных
осей так, как указано на рисунке,
составляем первые два уравнения
равновесия:
4
0
0
X
0
:
P
cos
30
N
sin
30
0
i
B
i 1
4
0
0
Y
0
:
P
sin
30
N
cos
30
Q NA 0
i
B
i 1

10.

• При составлении уравнения для
моментов с целью его упрощения за
центр приведения обычно берут
такую точку, через которую
проходят линии действия возможно
большего числа неизвестных сил.
Моменты этих сил относительно
такой точки равны нулю. В
рассматриваемой задаче это точка
В, в которой приложены
неизвестные силы NB и Р.
• Вес стержня приложен в его центре
тяжести, который совпадает с
серединой стержня. Если его плечо
относительно точки В обозначить а,
то плечо силы NА равно 2а
• Если положительным объявить момент, вращающий стержень
против часовой стрелки вокруг точки В, то уравнение для
моментов примет вид NA 2а - Q а = 0 или 2NA - Q = 0

11.

После подстановки всех необходимых чисел система
уравнений равновесия выглядят следующим образом:
3
1
NB 0
P
2
2
1
3
100 N A 0
P NB
2
2
2 N A 100 0
Из этой системы
величины:
определяются
все
неизвестные
N A 50 H; P 25 H; N B 25 3 43,3 H

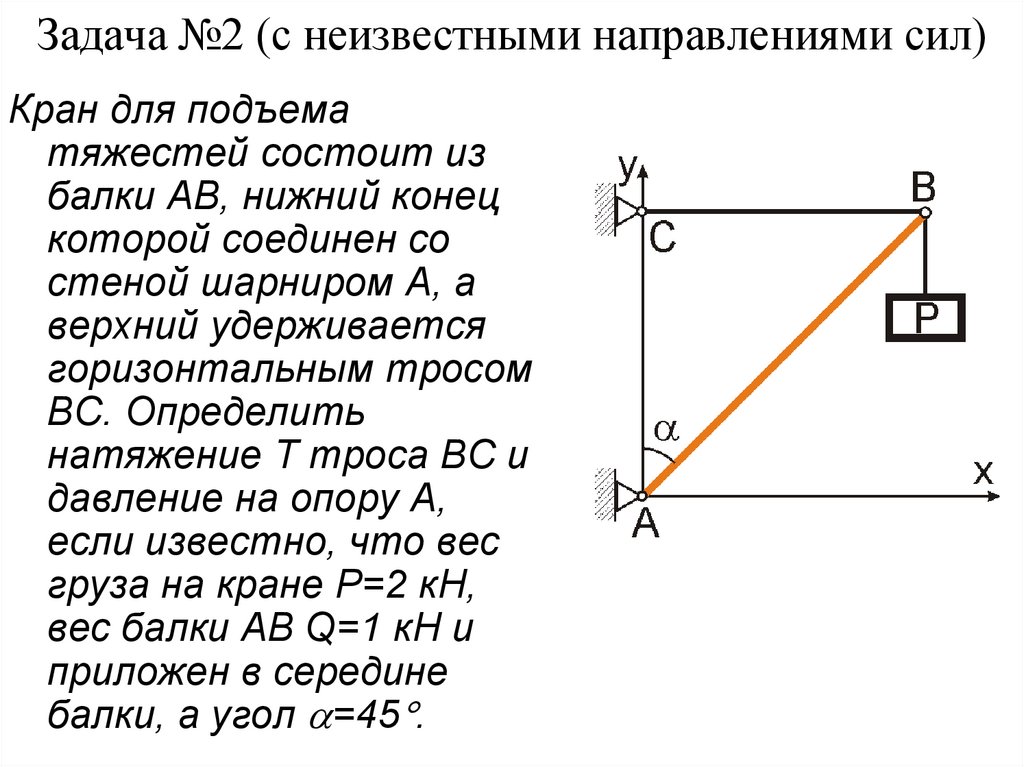
12. Задача №2 (с неизвестными направлениями сил)

Кран для подъема
тяжестей состоит из
балки АВ, нижний конец
которой соединен со
стеной шарниром А, а
верхний удерживается
горизонтальным тросом
ВС. Определить
натяжение Т троса ВС и
давление на опору А,
если известно, что вес
груза на кране Р=2 кН,
вес балки АВ Q=1 кН и
приложен в середине
балки, а угол =45 .

13.

• Решение задачи начинается с
расстановки всех сил,
действующих на балку АВ.
Такими являются:
• вес груза Р = 2 кН
• сила натяжения каната ВС
(сейчас неизвестна)
• вес балки Q=1 кН,.
• Направление реакции шарнирной опоры А невозможно
определить по условию задачи. Поэтому эта реакция заменяется
двумя силами, направленными вдоль координатных осей: Х и Y:
• Выбрав направления координатных осей так, как указано на
рисунке, составляем первые два уравнения равновесия:
5
X 0 : T X 0
i 1
i
5
Y 0 : P Q Y 0
i 1
i

14.

• При составлении уравнения для
моментов с целью его упрощения за
центр приведения обычно берут
такую точку, через которую
проходят линии действия возможно
большего числа неизвестных сил. В
рассматриваемой задаче это точка
А, в которой приложены
неизвестные силы Х и Y.
• Как видно из рисунка, плечи
остальных сил равны:
hP AB sin ; hQ 0,5 AB sin ; hT AB cos ;
• Если положительным объявить момент, вращающий балку
против часовой стрелки вокруг точки А, и иметь в виду, что
=45 , то уравнение для моментов примет вид
2
2
2
T AB
P AB
Q 0,5 AB
0 или
2
2
2
T P 0,5 Q 0

15.

После подстановки всех необходимых чисел система
уравнений равновесия выглядят следующим образом:
X T 0
Y 1 2
T 2 0,5 1
Из этой системы
величины:
определяются
все
неизвестные
Y 3 кH; T 2,5 кH; X 2,5 кH

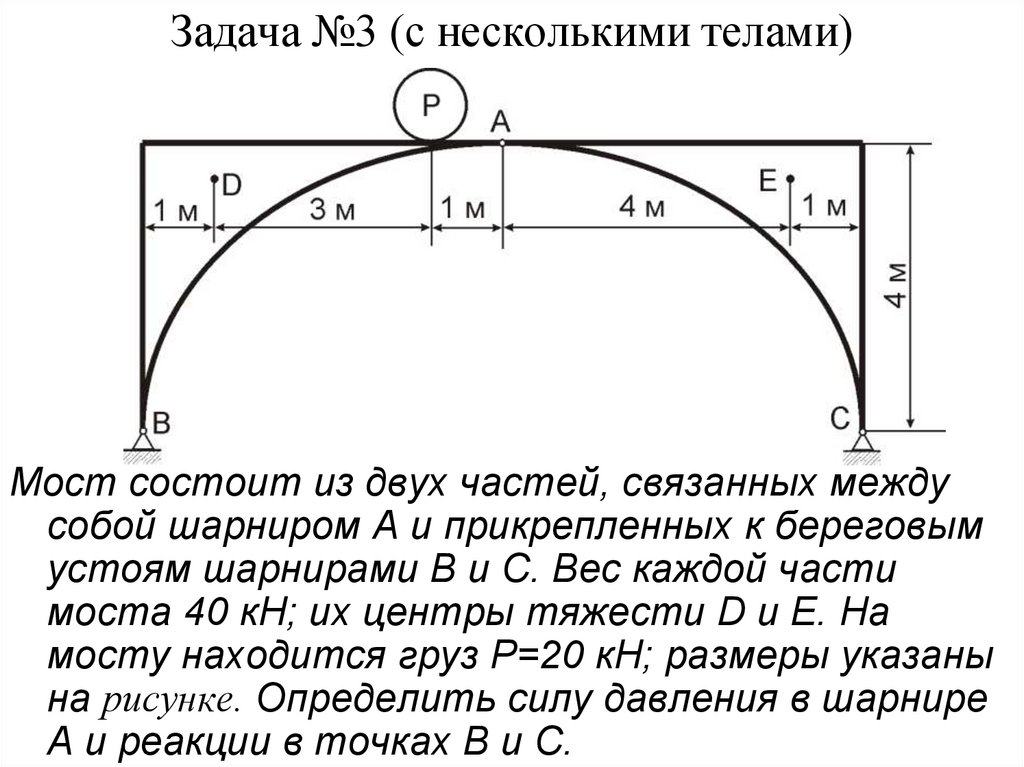
16. Задача №3 (с несколькими телами)

Мост состоит из двух частей, связанных между
собой шарниром А и прикрепленных к береговым
устоям шарнирами В и С. Вес каждой части
моста 40 кН; их центры тяжести D и Е. На
мосту находится груз Р=20 кН; размеры указаны
на рисунке. Определить силу давления в шарнире
А и реакции в точках В и С.

17. Равновесие левой части моста

На левую часть моста
действуют следующие силы:
• вес самой этой части Q,
приложенный в точке D
• вес лежащего на ней груза Р
• реакция опоры B (XB, YB)
• реакция шарнира А (XА, YА)
Уравнения равновесия для левой
части выглядят следующим
образом:
X i 0
Yi 0
L 0
i
XB X A 0
YB Q P YA 0
Q 1 P 4 X 4 Y 5 0
A
A
Моменты, входящие в последнее уравнение, вычислены
относительно точки В; необходимые размеры взяты из рисунка.

18. Равновесие правой части моста

На правую часть моста действуют следующие силы:
• вес самой этой части Q, приложенный в точке Е
• реакция опоры С (XС, YС)
• реакция шарнира А. Согласно III
закону Ньютона, в шарнире
действуют те же силы (XА, YА),
но направленные
противоположно.
Уравнения равновесия для
правой части:
X i 0
Yi 0
L 0
i
X A XC 0
YC Q YA 0
Q 1 X 4 Y 5 0
A
A
Моменты, входящие в последнее уравнение, вычислены
относительно точки С; необходимые размеры взяты из рисунка.

19.

При объединении обоих систем уравнений получается
система из 6 уравнений для 6 неизвестных: ХА, YA, ХB,
YB, ХС, YС. После подстановки чисел она выглядит
следующим образом:
X B X A 0
Y Y 60
A
B
4X A 5Y A 120
X A X C 0
Y C Y A 40
4X A 5Y A 40
Решения этой системы – следующие: ХА= ХB= ХС=20 кН,
YA=8 кН, YB=52 кН, YС=48 кН.