Равновесие системы тел

1.

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 7.
РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ
Кафедра теоретической механики

2. План лекции

И мудрое сферическое здание
народы и века переживет.
Осип Мандельштам
Введение
Расчет ферм
Ферма. Основные понятия
Определение реакций связей
Определение усилий в стержнях методом
вырезания узлов
Определение усилий в стержнях методом
сечений (Риттера)
Расчет составных конструкций
Заключение

3. На предыдущих лекциях

Аксиомы статики
равновесие абсолютно твердого тела под действием двух
сил (аксиома 1)
третий закон Ньютона (аксиома 4)
аксиома отвердевания (аксиома 5)
аксиома о связях
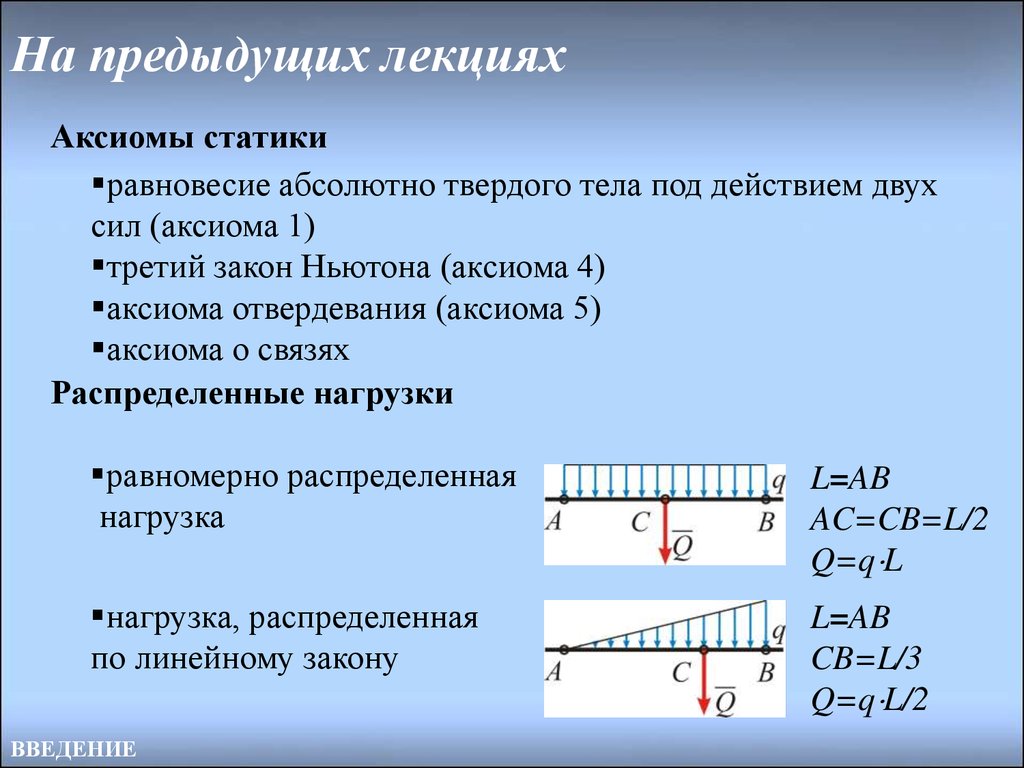
Распределенные нагрузки
равномерно распределенная
нагрузка
L=AB
AC=CB=L/2
Q=q L
нагрузка, распределенная
по линейному закону
L=AB
CB=L/3
Q=q L/2
ВВЕДЕНИЕ

4. На предыдущих лекциях

Связи и реакции связей
гладкая поверхность
гладкая поверхность с
угловой точкой
идеальная нить
идеальный стержень
подвижный
цилиндрический шарнир
неподвижный
цилиндрический шарнир
жесткая заделка
Уравнения равновесия плоской системы сил (одна из форм)
n
n
k 1
k 1
Fkx 0, Fky 0,
M 0 Fk 0
n
k 1
Момент силы относительно точки на плоскости
M 0 F F h
ВВЕДЕНИЕ

5. Цель лекции

Ознакомление с методом расчета
равновесия конструкций
ВВЕДЕНИЕ

6. Идея метода

Система тел будет находится в
равновесии тогда и только тогда, когда
в равновесии находится каждое из
составляющих ее тел.
ВВЕДЕНИЕ

7.

Применение фермовых конструкций
Мосты
Опоры ЛЭП
Подъемные
краны
Металлические
каркасы зданий

8. Расчет ферм

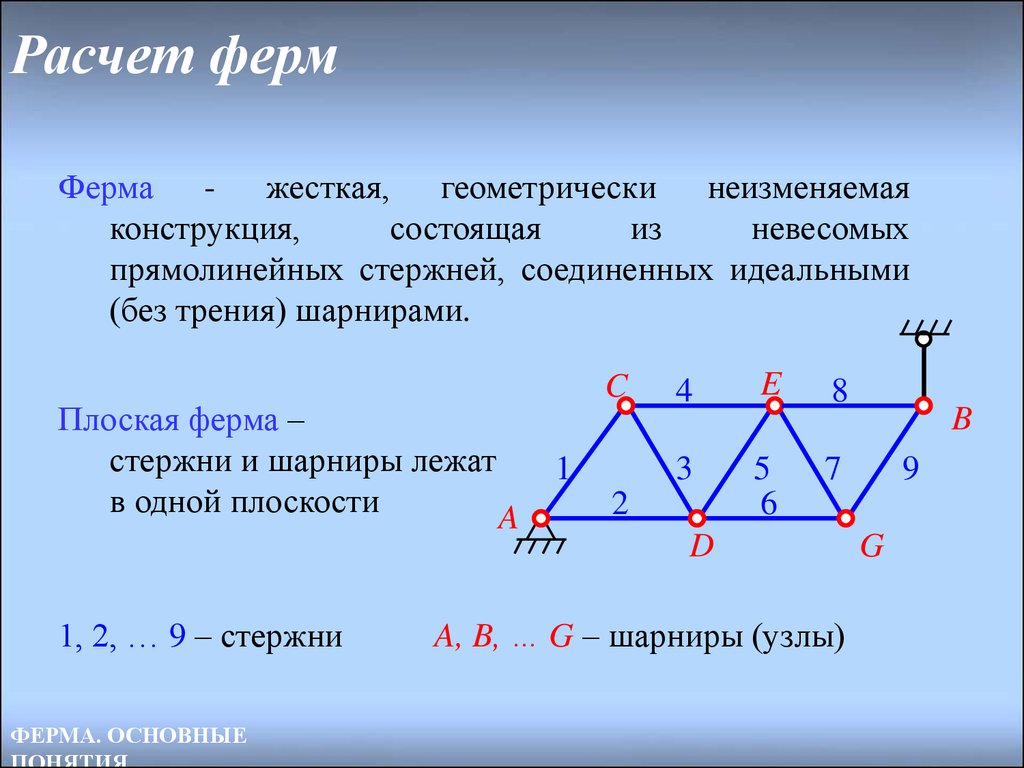
Ферма - жесткая, геометрически неизменяемая
конструкция,
состоящая
из
невесомых
прямолинейных стержней, соединенных идеальными
(без трения) шарнирами.
Плоская ферма –
стержни и шарниры лежат
в одной плоскости
A
1, 2, … 9 – стержни
ФЕРМА. ОСНОВНЫЕ
C
1
4
E
3
5
6
2
8
B
7
D
A, B, … G – шарниры (узлы)
9
G

9. Расчет ферм

В общем случае каждый стержень фермы
испытывает как продольные (сжатие и растяжение),
так и поперечные нагрузки, изгибающие стержень.
Поперечные – наиболее опасные,
основная задача при конструировании
минимизировать именно их.
поэтому
ферм –
Для этого
стержни должны быть соединены шарнирами.
ФЕРМА. ОСНОВНЫЕ ПОНЯТИЯ

10.

Расчет ферм
Докажем, что в идеализированной ферме, у
которой все усилия приложены к узлам,
стержни испытывают только продольные
нагрузки
УТВЕРЖДЕНИЕ О ПРОДОЛЬНОСТИ НАГРУЗОК

11.

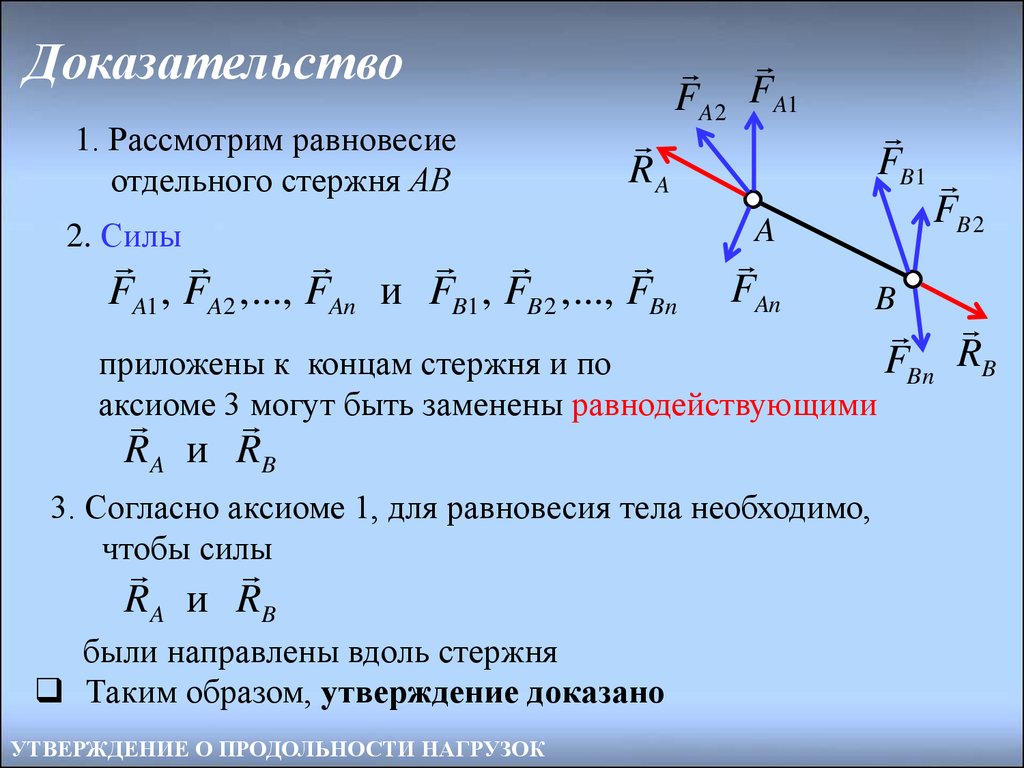
Доказательство
1. Рассмотрим равновесие
отдельного стержня АВ
RA
2. Силы
FA 2 FA1
FA1 , FA2 , ..., FAn и FB1 , FB 2 , ..., FBn
FB1
FB 2
A
FAn
B
приложены к концам стержня и по
аксиоме
3 могут быть заменены равнодействующими
R A и RB
3. Согласно аксиоме 1, для равновесия тела необходимо,
чтобы силы
R A и RB
были направлены вдоль стержня
Таким образом, утверждение доказано
УТВЕРЖДЕНИЕ О ПРОДОЛЬНОСТИ НАГРУЗОК
FBn RB

12. Расчет ферм

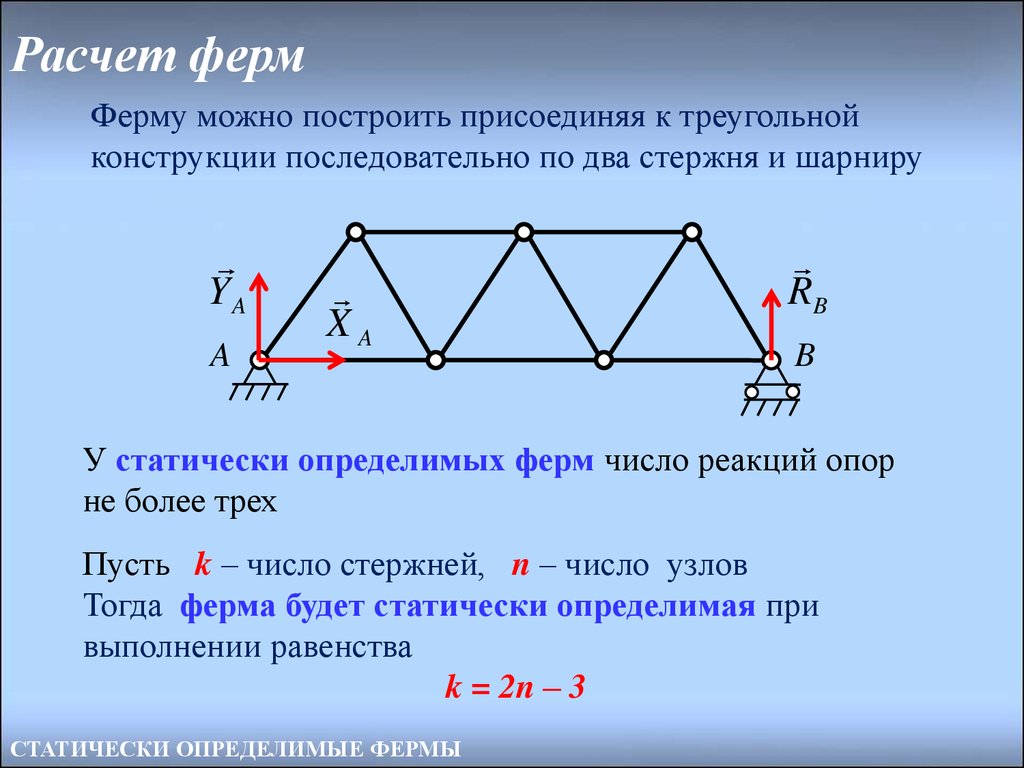
Ферму можно построить присоединяя к треугольной
конструкции последовательно по два стержня и шарниру
YA
A
XA
RB
B
У статически определимых ферм число реакций опор
не более трех
Пусть k – число стержней, n – число узлов
Тогда ферма будет статически определимая при
выполнении равенства
k = 2n – 3
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ФЕРМЫ

13.

Расчет ферм
Для расчета ферм необходимо
Найти реакции опор с использованием
аксиомы отвердевания и 3-х уравнений
равновесия
Определить усилия в стержнях фермы
методом вырезания узлов или
методом сечений ( Риттера)
РАСЧЕТ ФЕРМ

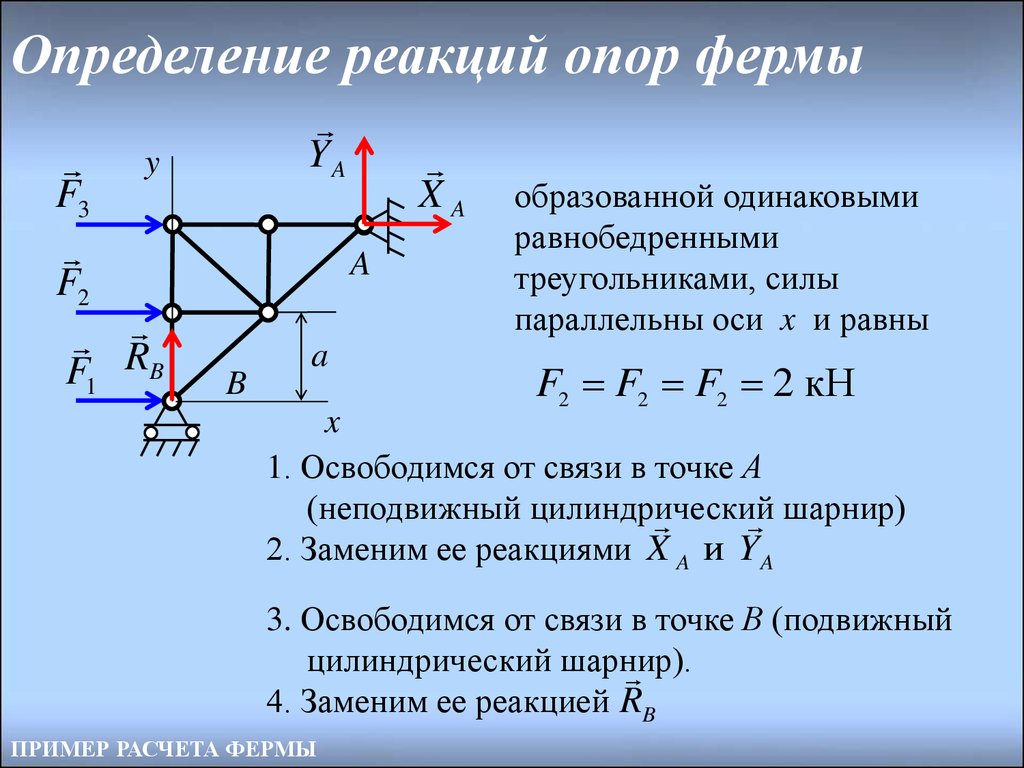
14. Определение реакций опор фермы

y
F3
F2
R
F1 B
YA
XA
A
B
a
образованной одинаковыми
равнобедренными
треугольниками, силы
параллельны оси x и равны
F2 F2 F2 2 кН
x
1. Освободимся от связи в точке А
(неподвижный цилиндрический
шарнир)
2. Заменим ее реакциями X A и Y A
3. Освободимся от связи в точке В (подвижный
цилиндрический шарнир).
4. Заменим ее реакцией RB
ПРИМЕР РАСЧЕТА ФЕРМЫ

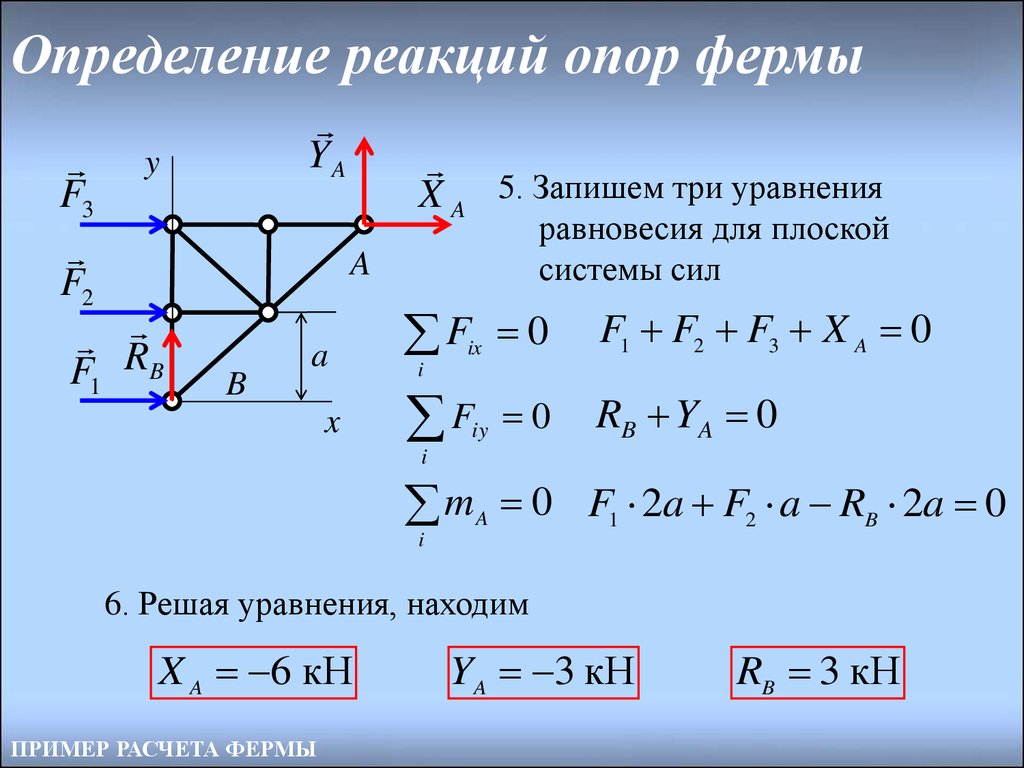
15. Определение реакций опор фермы

y
F3
F2
R
F1 B
YA
X A 5. Запишем три уравнения
равновесия для плоской
системы сил
A
B
a
x
F
ix
0
F1 F2 F3 X A 0
0
RB YA 0
i
F
iy
i
m
A
0 F1 2a F2 a RB 2a 0
i
6. Решая уравнения, находим
X A 6 кН
ПРИМЕР РАСЧЕТА ФЕРМЫ
YA 3 кН
RB 3 кН

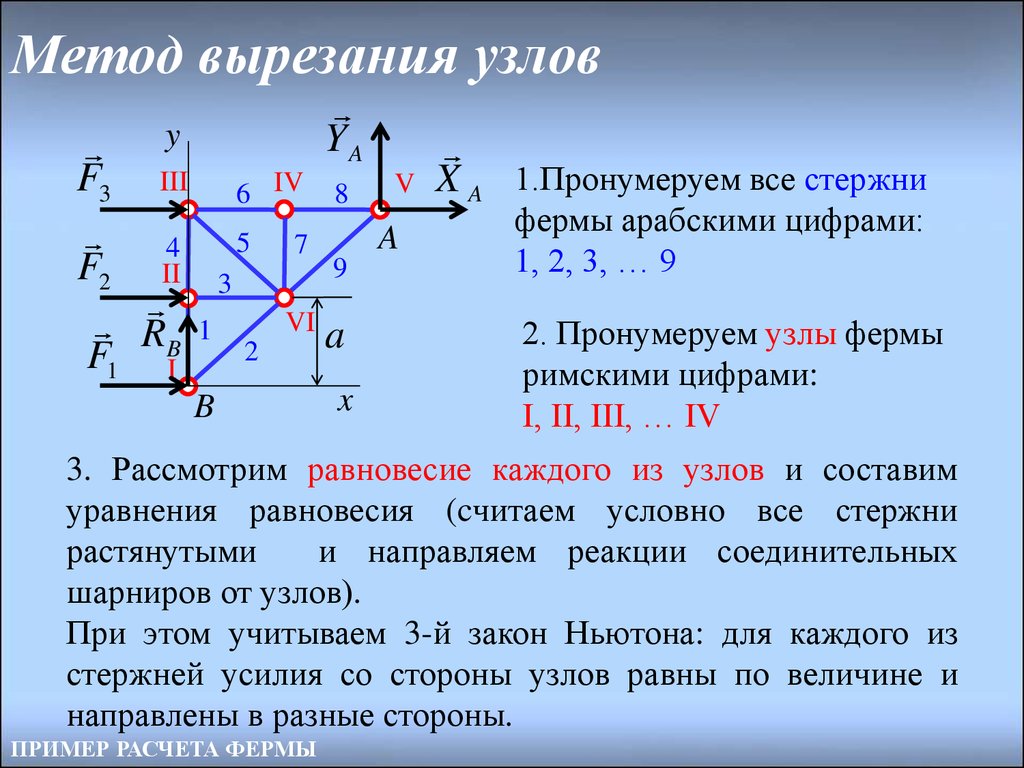
16. Метод вырезания узлов

y
F3 III 6
5
4
F2 II 3
R 1
2
F1 BI
YA
IV
7
VI
B
8
V
A
9
a
x
X A 1.Пронумеруем все стержни
фермы арабскими цифрами:
1, 2, 3, … 9
2. Пронумеруем узлы фермы
римскими цифрами:
I, II, III, … IV
3. Рассмотрим равновесие каждого из узлов и составим
уравнения равновесия (cчитаем условно все стержни
растянутыми
и направляем реакции соединительных
шарниров от узлов).
При этом учитываем 3-й закон Ньютона: для каждого из
стержней усилия со стороны узлов равны по величине и
направлены в разные стороны.
ПРИМЕР РАСЧЕТА ФЕРМЫ

17. Метод вырезания узлов

F3
Начнем расчет с узла V, в котором сходятся
2-а стержня с неизвестными усилиями.
F2
Узел V
Fix 0 : X A S 8 S 9 cos 45 0 F1
YA
i
XA
8
S8 9
S9
Узел
IV
S 6 S8
S7
Узел
III
F3
S4
S6
S5
Fiy 0 :
Y A S9 sin 45 0
i
Fix 0 : S8 S6 0
i
Fiy 0 : S 7 0
i
F
0
:
S
F
S
cos
45
0
ix
6
3
5
i
Fiy 0 : S
i
ПРИМЕР РАСЧЕТА ФЕРМЫ
S
sin
45
0
4
5
y
YA
III 6 IV 8 V
4
7
A
5
XA
9
II 3
1 VI a
RB 2
x
IB

18. Метод вырезания узлов

Узел II
S
F2 4 S3
S1
Fix 0 : F2 S3 0
i
Fiy 0 : S4 S1 0
F3
F2
F1
i
Узел I
F1 RB
Fix 0 :
S1
S2
y
YA
III 6 IV 8 V
4
7
A
5
XA
9
II 3
RB 1 2 VI a
x
IB
F1 S2 cos 45 0
i
Fiy 0 :
S1 RB S2 sin 45 0
i
Узел VI
S3
S5 S 7
S2
S9
F
0
:
S
S
cos
45
S
cos
45
S
cos
45
0
ix
3
2
5
9
i
S
S
sin
45
S
sin
45
S
sin
45
0
Fiy 0 : 7 2
5
9
i
Последний узел (узел VI) можно использовать для проверки
решения: уравнения при подстановке найденных усилий в
ПРИМЕР РАСЧЕТА ФЕРМЫ стержнях должны удовлетворяться тождественно

19.

Метод сечений (Риттера)
Удобен если требуется определить
усилия в каких-то отдельных
стержнях фермы, например, 6, 7, 9
(число стержней должно быть не
более трех)
Последовательность действий
y
F3
4
F2
R
F1 B
YA
z
6 IV
5
7
3
1
B
VI
2
V
8
A
9
z
a
x
1. Проведем сквозное сечение z–z через стержни 6,7,9.
2. Пользуясь принципом отвердевания, рассмотрим
равновесие одной из частей фермы, например, правой. Для
этого составляем 3 уравнения моментов сил относительно
точек в которых пересекаются 2 стержня с неизвестными
усилиями - IV, V(А), VI.
ПРИМЕР РАСЧЕТА ФЕРМЫ
XA

20.

Метод сечений (Риттера)
YA
y z
6 IV
V
S6 7 A
S7
9 S9
VI
XA
z
m
0:
S7 0
IV
0:
aYA aS9 sin 45 0
VI
0:
a Y A a S6 a X A 0
A
i
m
i
m
i
Решив систему уравнений находим усилия в стержнях 6,7,9
Полученные результаты можно использовать для проверки
результатов, полученных методом вырезания узлов.
Всегда, если значение усилия в стержне получено со знаком
« », то стержень не растянут, а сжат.
ПРИМЕР РАСЧЕТА ФЕРМЫ

21.

Примеры составных конструкций
Триумфальные ворота
Москва,
1829-1834 гг.
1-ый панельный дом
Новосибирск, 1960 г.
Стоунхендж, Англия,
2440-2100 гг. до н. э.
Дмитровский
мост,
Новосибирск,
1971-1780 гг.
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ

22.

Расчет составных конструкций
Последовательность действий
1. Освободившись от связей рассматриваем
равновесие каждого из тел конструкции.
2. Составляем для каждого тела уравнения
равновесия (наряду с активными силами
учитываем силы реакций внешних и
внутренних связей).
Такой способ расчета конструкции называют
методом расчленения.
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ

23.

Статически определимая конструкция
Если общее число независимых уравнений больше
или равно общему числу неизвестных (реакций
связей), то такая конструкция называется
статически определимой.
Для плоской конструкции, состоящей из двух тел,
мы можем составить шесть независимых
уравнений равновесия (по 3 для каждого из двух
тел) и определить из них шесть неизвестных.
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ

24.

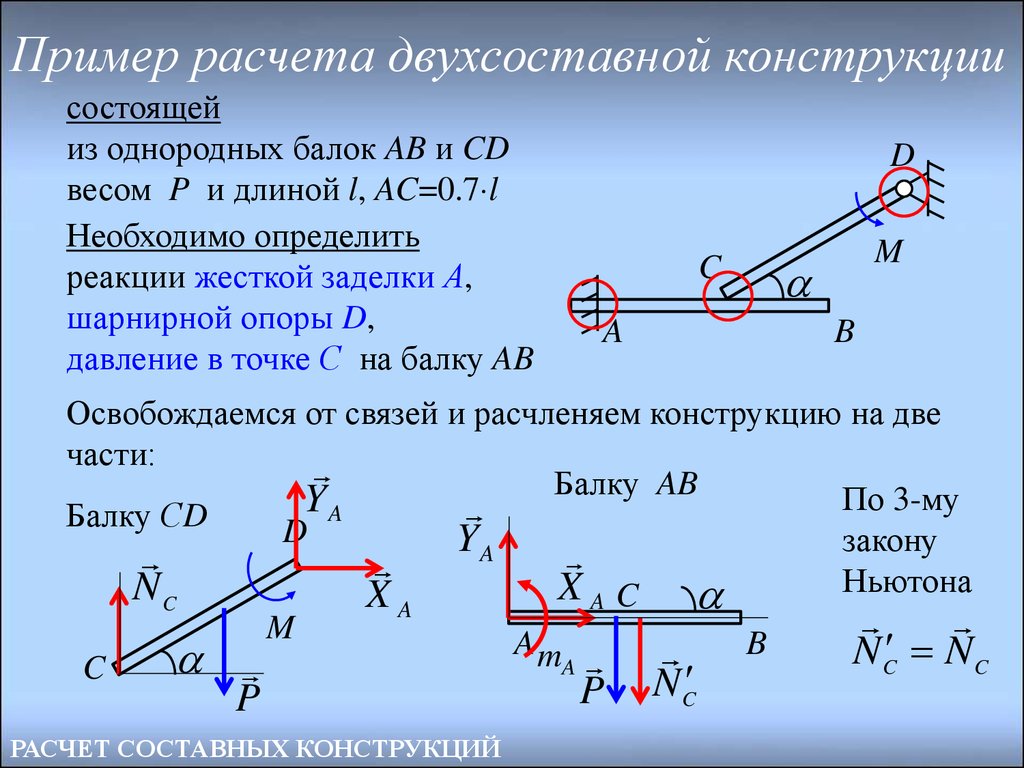
Пример расчета двухсоставной конструкции
состоящей
из однородных балок AB и CD
весом P и длиной l, AC=0.7 l
Необходимо определить
реакции жесткой заделки А,
шарнирной опоры D,
давление в точке С на балку AB
D
C
A
M
B
Освобождаемся от связей и расчленяем конструкцию на две
части:
Балку AB
По 3-му
Y
A
Балку СD
D
YA
закону
Ньютона
XA C
NC
XA
M
Am
B
N C N C
A
C
P
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ
P
NC

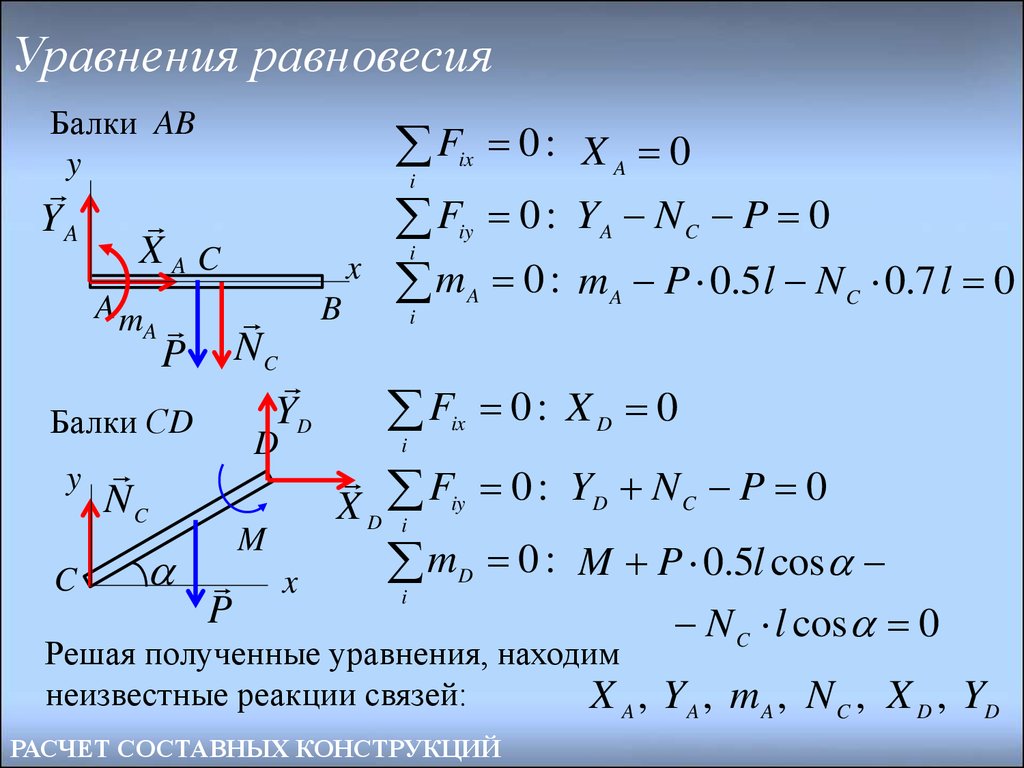
25.

Уравнения равновесия
Балки AB
y
YA
P
Балки СD
y
C
NC
ix
0: XA 0
iy
0 : YA N C P 0
i
XA C
Am
A
F
F
m
x
NC
YD
D
B
i
A
0 : mA P 0.5 l N C 0.7 l 0
i
F
ix
0: XD 0
i
F 0: Y N P 0
D
C
X D i iy
M
mD 0 : M P 0.5l cos
x
i
P
N C l cos 0
Решая полученные уравнения, находим
неизвестные реакции связей:
X A,
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ
YA , mA , N C , X D , YD

26.

Проверка
решения проводится с применением аксиомы отвердевания,
вследствие чего связь в точке C считаем «замороженной».
Расчетная схема с учетом этого примет вид
D
y
YA
С
XA
Am
A
P
m
i
YD
XD
M
P x
B
F
F
ix
0:
iy
0:
i
i
A
Для нее при подстановки
решения
X A , YA , mA , N C , X D , YD
должны тождественно
удовлетворятся уравнения :
XA XD 0
YA YD 2 P 0
0 : m A M X D l sin YD (0.7 cos )l
P 0.5 l P (0.7 0.5 cos ) l 0
РАСЧЕТ СОСТАВНЫХ КОНСТРУКЦИЙ

27. Заключение

1. Сегодня мы освоили метод расчета конструкций,
основанный на идее, что
система тел находится в
равновесии тогда и только тогда, когда в равновесии
находится каждое из составляющих ее тел
2. С применением этого метода для конкретных примеров
нами были произведены расчеты реакций опор и усилий в
стержнях фермы и реакций опор двухсоставной
конструкции.
3. В примерах рассматривали отдельно равновесие каждой
части двухсоставной конструкции, каждого узла (метод
вырезания узлов) или части (метод Риттера) фермы.
ЗАКЛЮЧЕНИЕ

28. Вопросы для самоконтроля

1.
2.
3.
4.
5.
6.
7.
8.
Привести примеры использования ферм в
строительной технике.
Какова последовательность расчета ферм?
Какие методы расчета усилий в стержнях фермы Вы
знаете?
Как проводят сечение при расчете методом Риттера?
В чем заключается преимущество метода Риттера?
В чем заключается метод расчленения?
Сколько независимых уравнений равновесия можно
записать для плоской системы сил?
Что понимают под статически определимой
конструкцией?
ЗАКЛЮЧЕНИЕ

29. Тема следующей лекции

Равновесие при наличии трения
«Если принять во внимание действие силы
трения в месте контакта лыж со снегом,
то для удержания равновесия лыжник
должен сместить центр тяжести назад
от линии перпендикуляра к склону.»
Самоучитель горнолыжника
ЗАКЛЮЧЕНИЕ

30. Спасибо за внимание!