Похожие презентации:
Условия параллельности и перпендикулярности прямых
1.
Пусть заданы две прямыеy k1 x b1
y k2 x b2
Выразим угол между этими прямыми через
их угловые коэффициенты.
2.
y2
1
2
1
x
3.
2 1k1 tg 1
k2 tg 2
tg 2 tg 1
tg tg ( 2 1 )
1 tg 1 tg 2
4.
k2 k1tg
1 k1 k2
Стрелка указывает, что угол отсчитывается
против часовой стрелки от прямой 1 к
прямой 2.
5.
Если прямые 1 и 2 параллельны, то0
k2 k1
0
1 k1 k2
tg 0
k1 k2
6.
Две прямые параллельны тогда итолько тогда, когда их угловые
коэффициенты равны.
7.
Если прямые 1 и 2 перпендикулярны, тоctg ctg
2
0
2
1 1 k1 k2
ctg
0
tg
k2 k1
1
k1
k2
8.
Две прямые перпендикулярнытогда и только тогда, когда их
угловые коэффициенты
обратны по величине и
противоположны по знаку.
9.
Если прямые заданы общими уравнениямиA1 x B1 y C1 0
A1
B1
A2
B2
A1 A2 B1 B2 0
A2 x B2 y C2 0
10.
Пусть даны две прямыеA1 x B1 y C1 0
A2 x B2 y C2 0
Если они не параллельны, то можно найти
точку их пересечения.
Т.к. эта точка принадлежит обеим прямым, то
ее координаты
должны удовлетворять
системе уравнений:
A1 x B1 y C1 0
A2 x B2 y C2 0
Решение этой системы дает
точку пересечения.
единственную
11.
ПРИМЕР.Составить уравнения прямых,
проходящих через точку А(2,1),
одна из которых параллельна,
а другая перпендикулярна
прямой
3x 2 y 2 0
12.
РЕШЕНИЕ:1. По условию параллельности прямых
k1 k 2
Найдем угловой
прямой:
коэффициент
заданной
3
3
3x 2 y 2 0 y x 1 k1
2
2
Тогда
3
3
k2
y x b
2
2
Т.к. точка А лежит на искомой прямой, то ее
координаты
удовлетворяют
этому
уравнению:
13.
31 2 b
2
b 2
И уравнение искомой прямой будет:
3
y x 2 2 y 3x 4 0
2
2. По условию перпендикулярности прямых
1
k1
k2
Найдем угловой
прямой:
коэффициент
искомой
14.
2k3
3
2
y x b
3
Снова координаты точки А удовлетворяют
этому уравнению:
2
1 2 b
3
7
b
3
И уравнение искомой прямой будет:
2
7
y x
3y 2x 7 0
3
3
15.
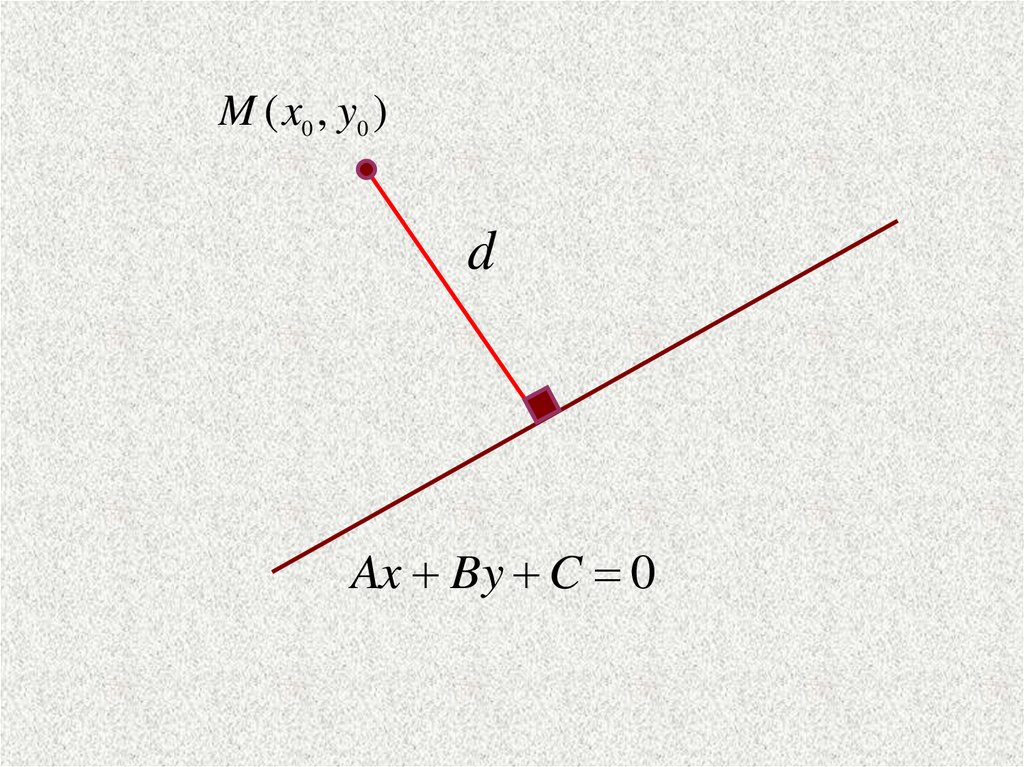
Пусть дана точка М(х0,у0) и прямаяAx By C 0
Под расстоянием от точки М до прямой
понимается длина перпендикуляра d,
опущенного из точки М на данную прямую.
d
Ax0 By0 C
A2 B 2
16.
M ( x0 , y0 )d
Ax By C 0
17.
ПРИМЕР.Найти расстояние между
параллельными прямыми
3x 4 y 24 0
3x 4 y 6 0
18.
РЕШЕНИЕ:Возьмем на одной из прямых, например, на
первой, произвольную точку А(0,6).
Тогда искомое расстояние это перпендикуляр
от точки А до второй прямой :
A 3 B 4 C 6
d
3 0 4 6 6
3 4
2
2
6

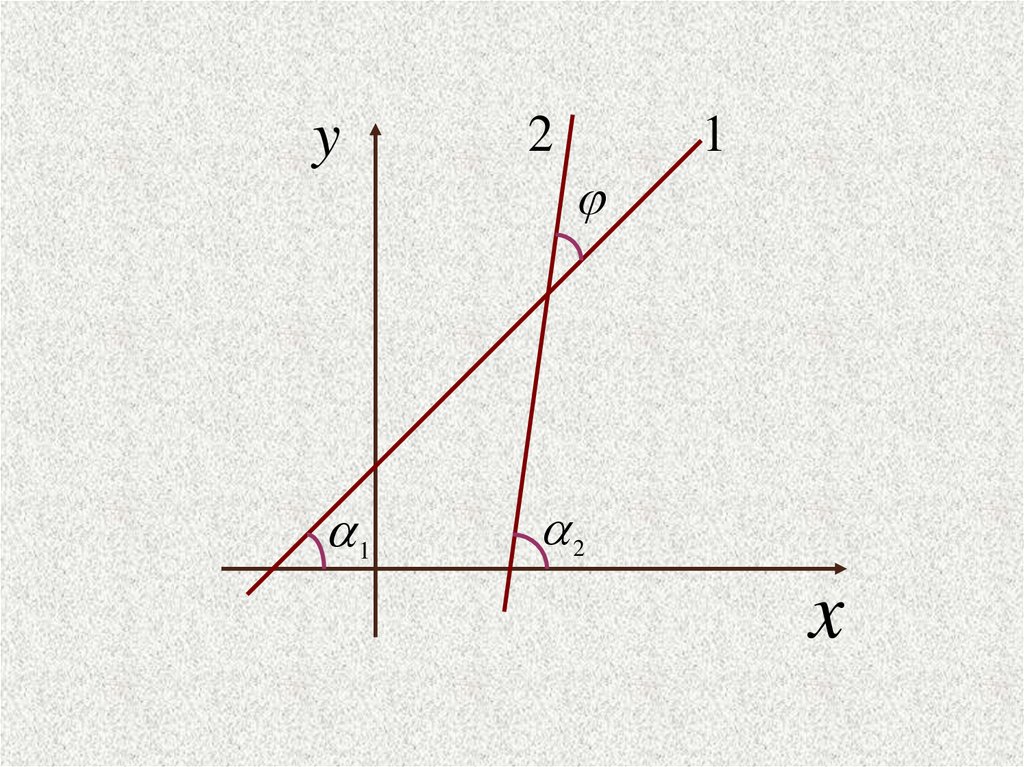















 Математика
Математика








