Похожие презентации:
Выбор и генерация признаков. Лекция №8
1. Выбор и генерация признаков
Лекция №82. Проклятие размерности
Выбор признаковГенерация признаков
Формирование новой системы признаков,
сохраняющей максимум информации о
выборке
Метод главных компонент
Метод независимых компонен
3. Выбор признаков
Что исключаем?Дублирующие признаки
Шумовые признаки
Критерии выбора признаков
Внешние
OLO, CV
Внутренние
Критерий Фишера
Методы перебора признаков
Жадные алгоритмы
Ad, Del, GRAD
Поиск в глубину и в ширину
Метод ветвей и границ, МГУА
Стохастический поиск
Генетический алгоритм, СПА
4. Критерии выбора признаков
Вероятность ошибкиP(i / x)] p( x)dx
Er= [1 max
i
Расстояние между распределениям
расстояние Махаланобиса JM=( 2- 1)T -1( 2- 1)
Мера энтропии
JE=- (p1j*logp1j+p2j*logp2j)
j
Мера Фишера
JF =( 2- 1)2/(S12+S22)
Компактность в широком смысле
5. Компактность
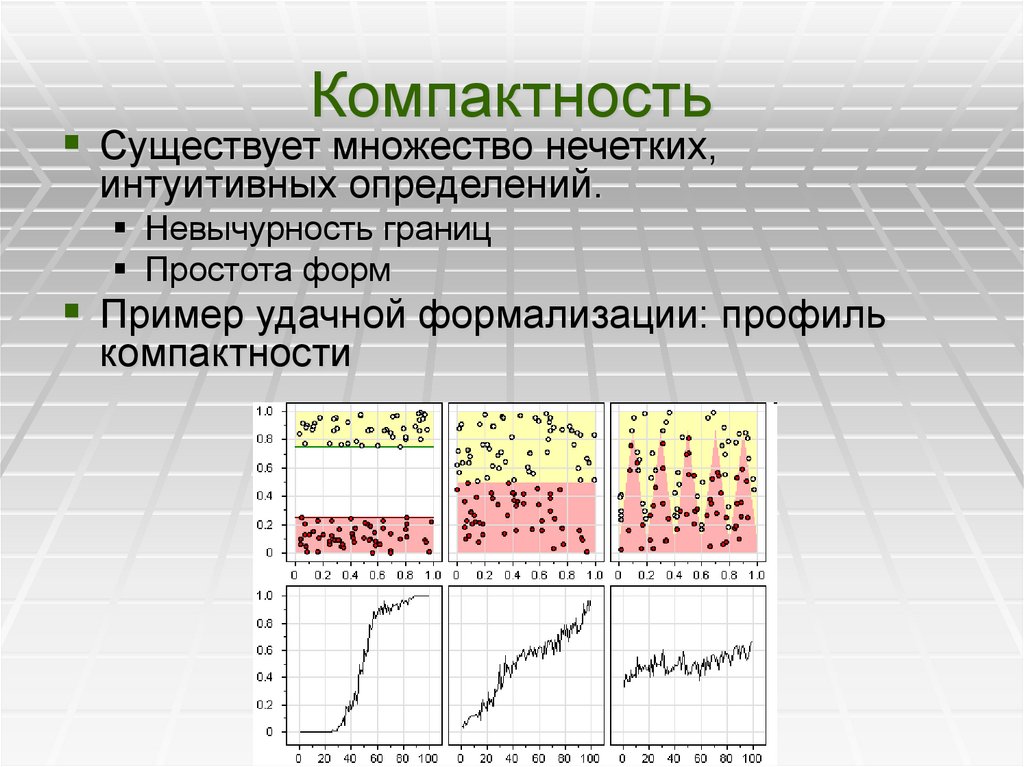
Существует множество нечетких,интуитивных определений.
Невычурность границ
Простота форм
Пример удачной формализации: профиль
компактности
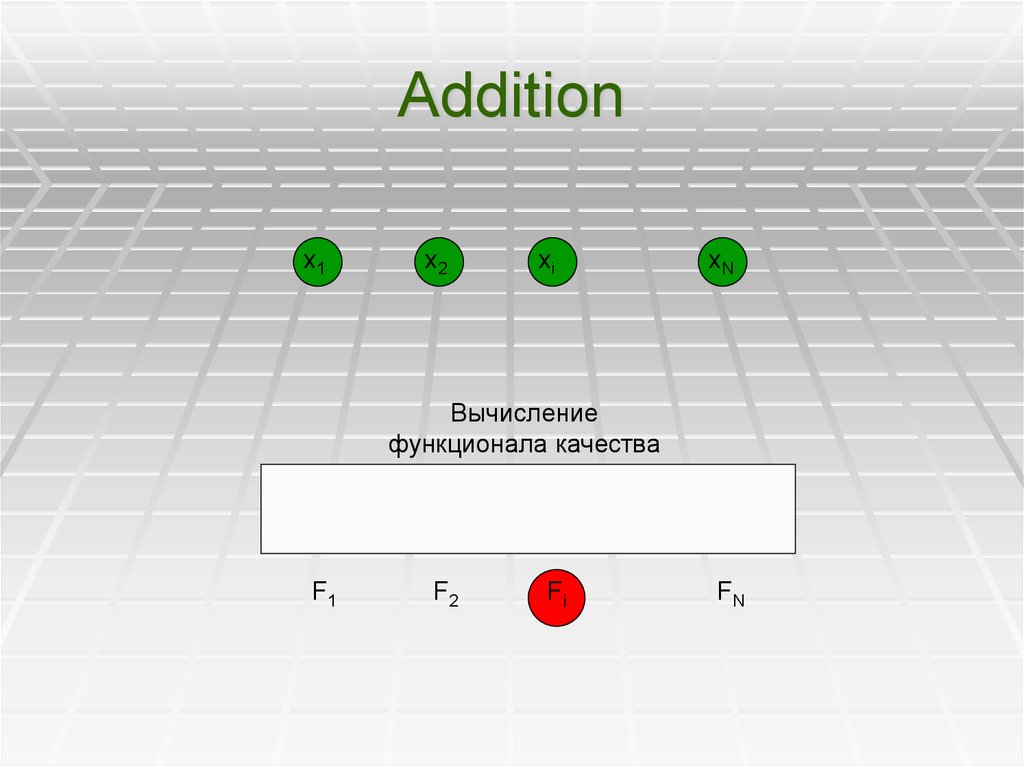
6. Addition
x1x2
xi
xN
Вычисление
функционала качества
F1
F2
Fi
FN
7. Deletion
x1x2
xi
xN
Вычисление
функционала качества
F1
F2
Fi
FN
8. AdDel,Grad
Чередование этапов Add и Del даютAdDel и DelAd
Использование вместо единичных
признаков гранул признаков небольшой
размерности
гранулы размерности 2 и 3 можно
формировать полным перебором
полезно в случае, если несколько
признаков информативны только вместе
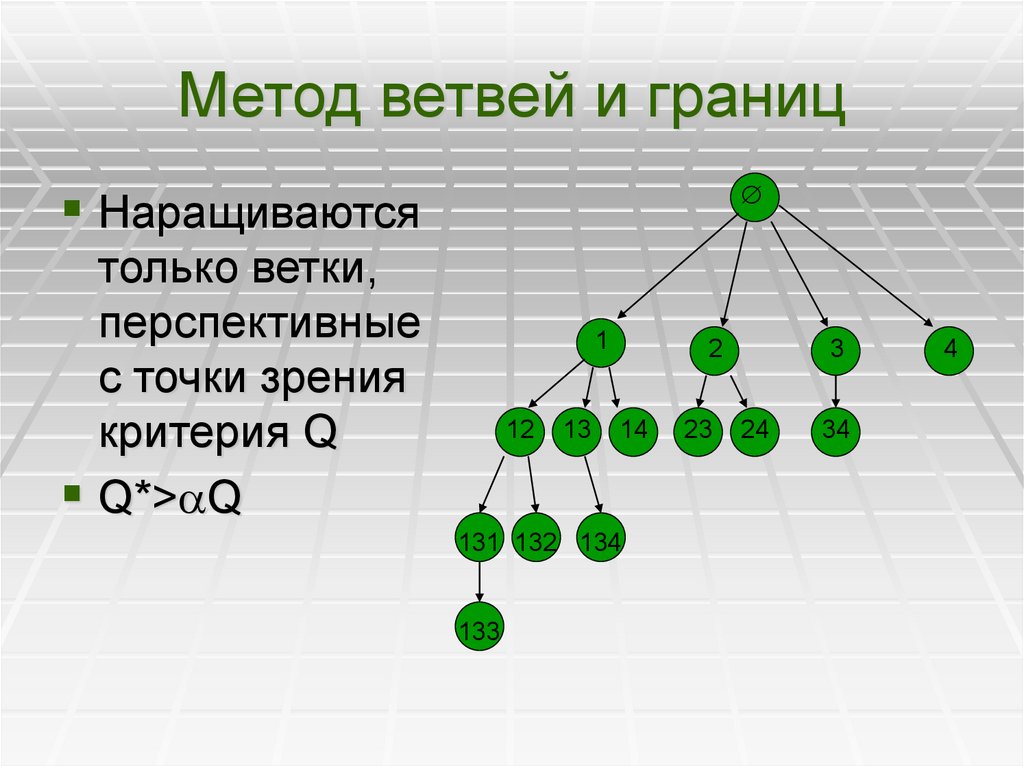
9. Метод ветвей и границ
Наращиваютсятолько ветки,
перспективные
с точки зрения
критерия Q
Q*> Q
1
12
13
2
14
131 132 134
133
23
3
24
34
4
10. Случайный поиск с адаптацией
Признаки выбираются случайноВероятность выбора признаков попадающих
в «хорошие» системы увеличивается
Вероятность выбора признаков, попадающих
в «плохие» системы уменьшается
Процесс останавливается после
стабилизации качества систем
х1
х2
х3
х4
х5
11.
Генерация признаков. Методглавных компонент
X={X1,X2,…,Xn} –исходная система признаков
Y={Y1,Y2,…,Yk} – сгенерированная система признаков
Yi=ai1*X1+ai2*X2+…+aij*Xj+…+ain*Xn
Y=AX, A-такое линейное ортогональное преобразование в
новую систему координат, для которого верно:
Выборочная дисперсия данных вдоль первой координаты Y1-максимальна;
Выборочная дисперсия данных вдоль второй координаты Y2- максимальна
при условии ортогональности первой координате (вторая главная
компонента);
…
Выборочная дисперсия данных вдоль значений k-ой координаты Yk максимальна при условии ортогональности первым k-1 координатам;
Сводится к задаче диагонализации ковариационной матрицы
Y1, Y2, …, Yk - собственные вектора эмпирической ковариационной
матрицы, расположенные в порядке убывания собственных значений.
Доля необъясненной дисперсии, показывает, какая часть информации
пропала в результате перехода.








 Математика
Математика








