21.11.24р Вписані та описані чотирикутники

1.

Тема:
Вписані та описані
чотирикутники.
Розв’язування задач.

2.

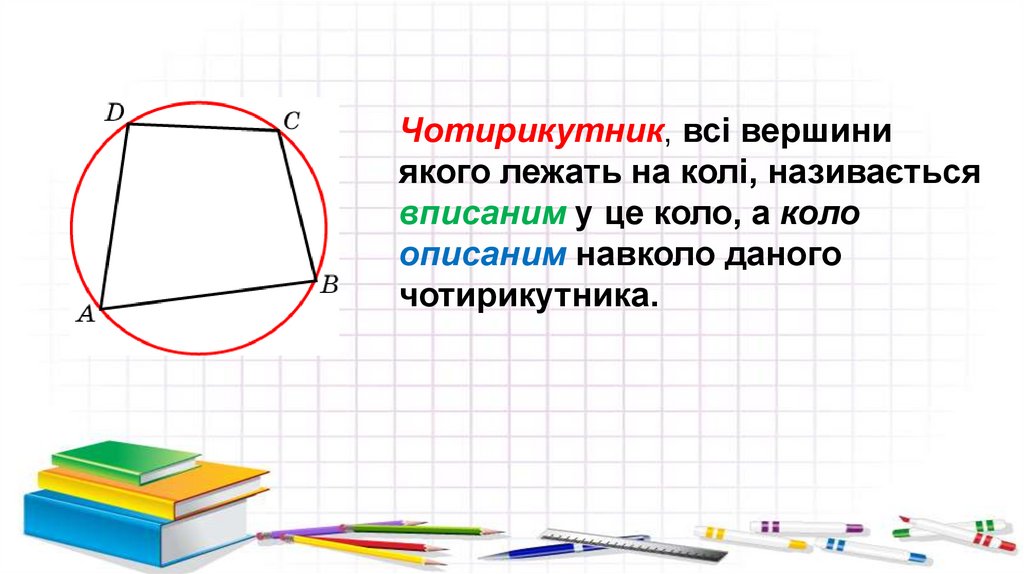
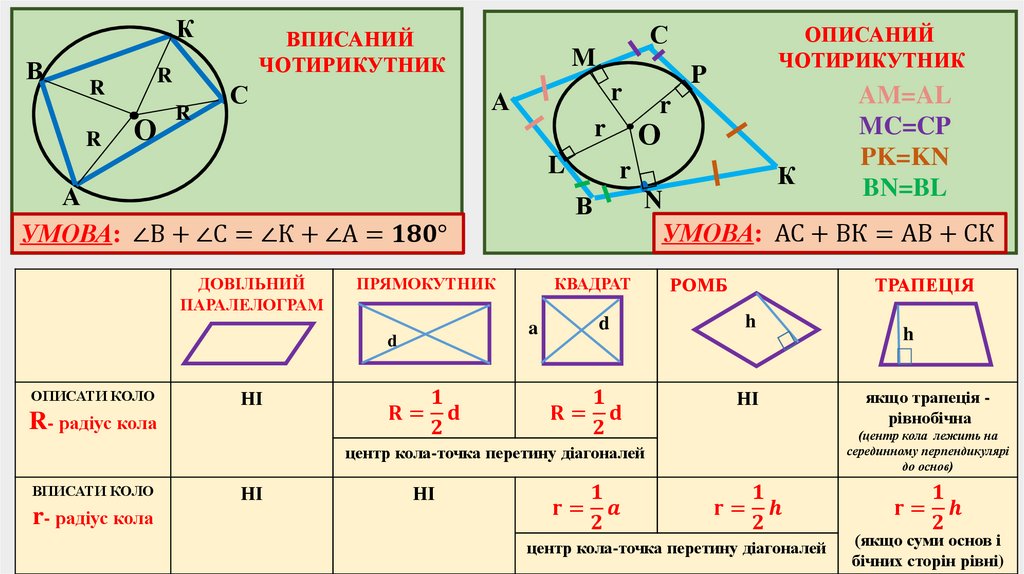
Чотирикутник, всі вершини
якого лежать на колі, називається
вписаним у це коло, а коло
описаним навколо даного
чотирикутника.

3.

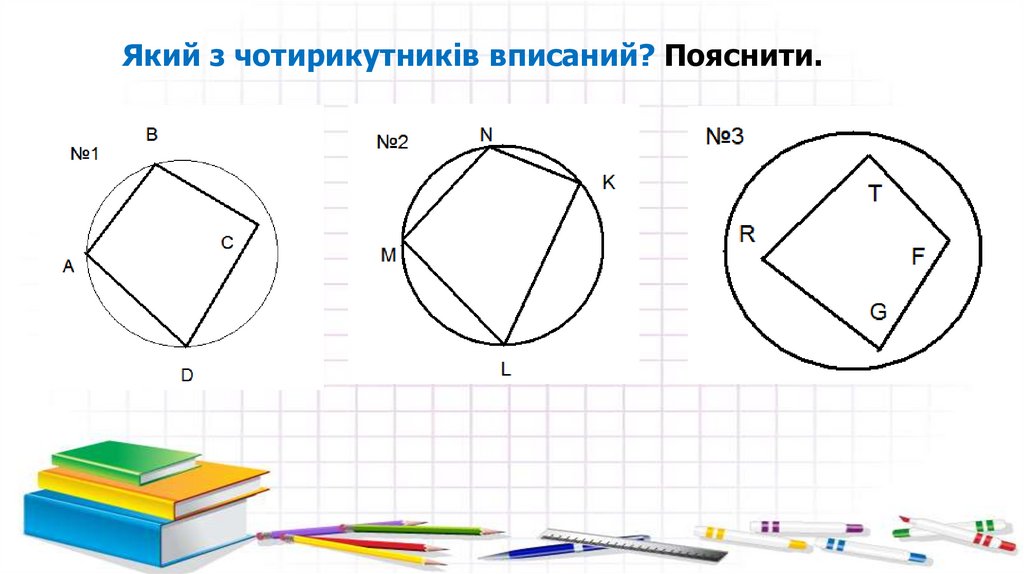
Який з чотирикутників вписаний? Пояснити.

4.

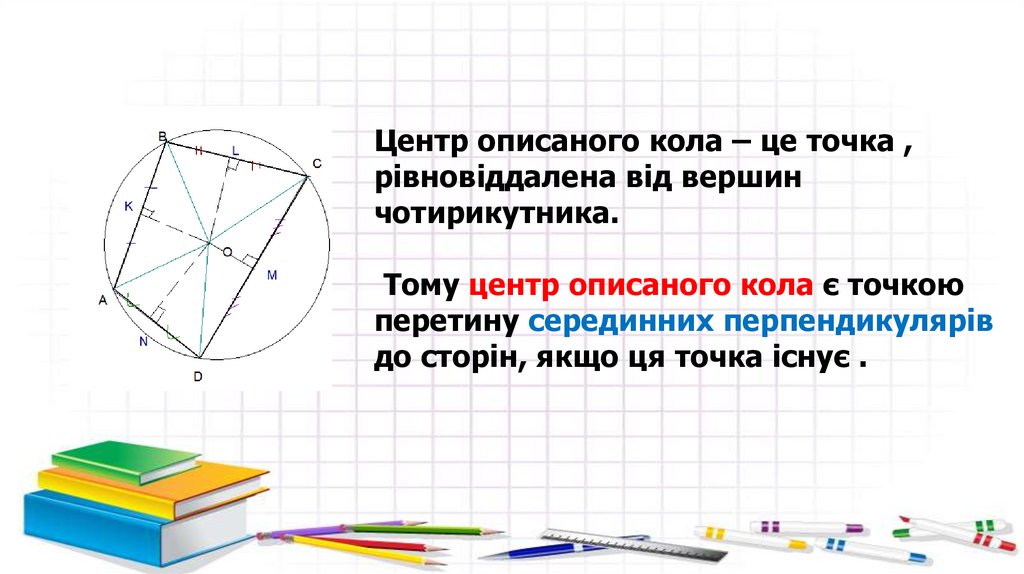
Центр описаного кола – це точка ,
рівновіддалена від вершин
чотирикутника.
Тому центр описаного кола є точкою
перетину серединних перпендикулярів
до сторін, якщо ця точка існує .

5.

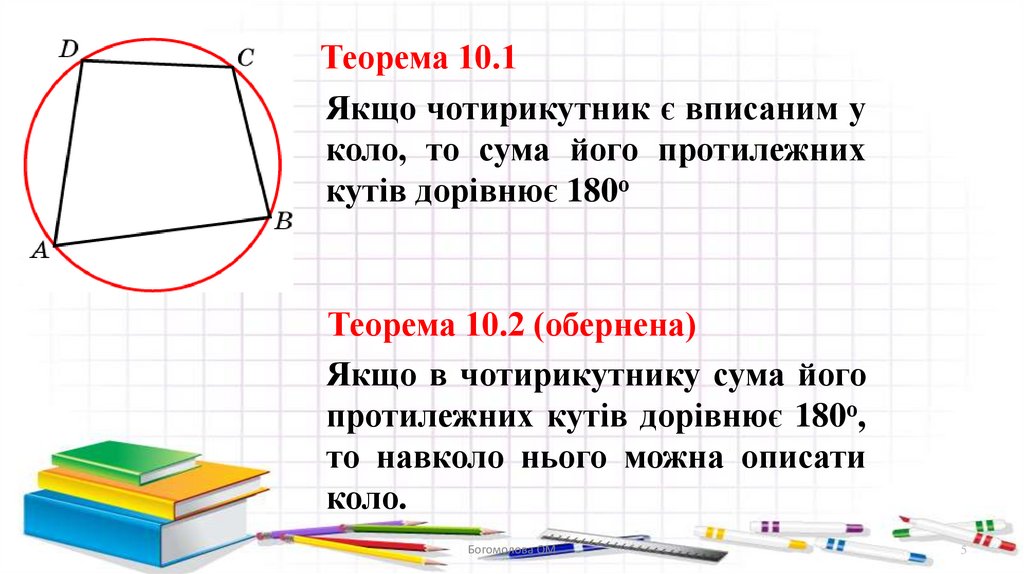
Теорема 10.1
Якщо чотирикутник є вписаним у
коло, то сума його протилежних
кутів дорівнює 180о
Теорема 10.2 (обернена)
Якщо в чотирикутнику сума його
протилежних кутів дорівнює 180о,
то навколо нього можна описати
коло.
Богомолова ОМ
5

6.

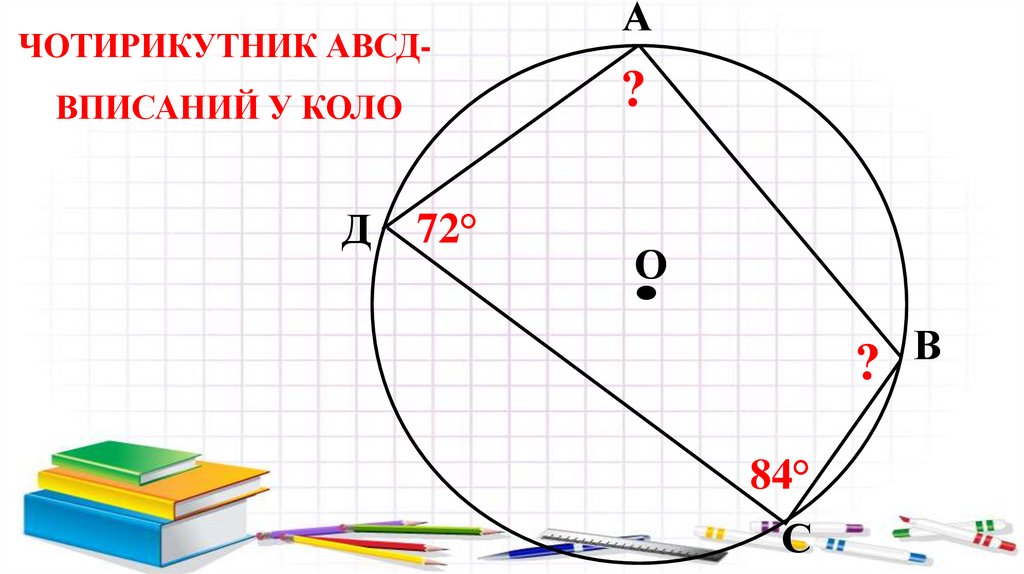
ЧОТИРИКУТНИК АВСД-
?
ВПИСАНИЙ У КОЛО
Д
А
72°
О
?
84°
С
В

7.

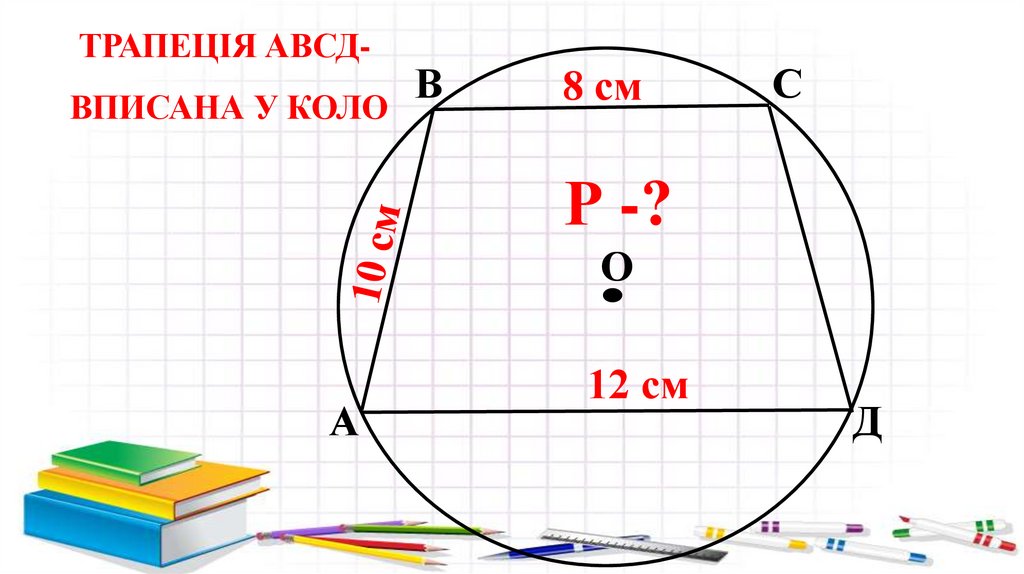
ТРАПЕЦІЯ АВСД-
В
ВПИСАНА У КОЛО
8 см
С
Р -?
О
А
12 см
Д

8.

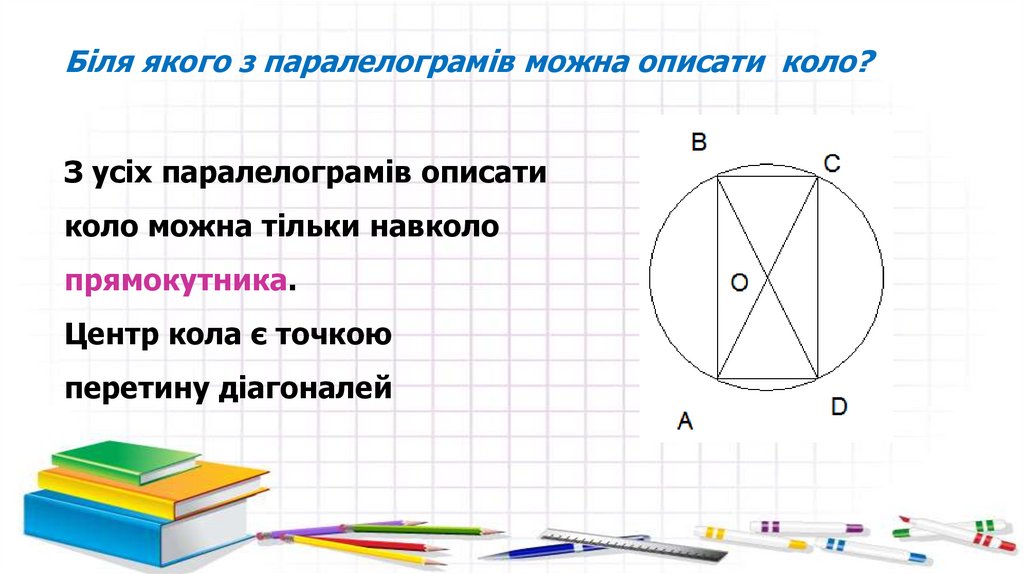
Біля якого з паралелограмів можна описати коло?
З усіх паралелограмів описати
коло можна тільки навколо
прямокутника.
Центр кола є точкою
перетину діагоналей

9.

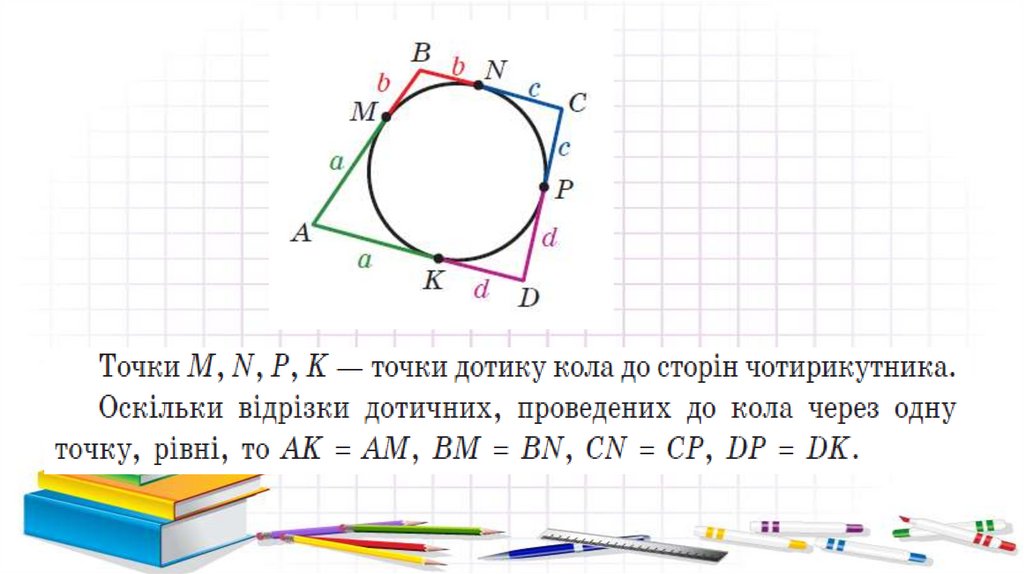
Чотирикутник, всі
сторони якого
дотикаються до кола,
називається описаним
навколо цього кола, а
коло називається
вписаним в
чотирикутник.

10.

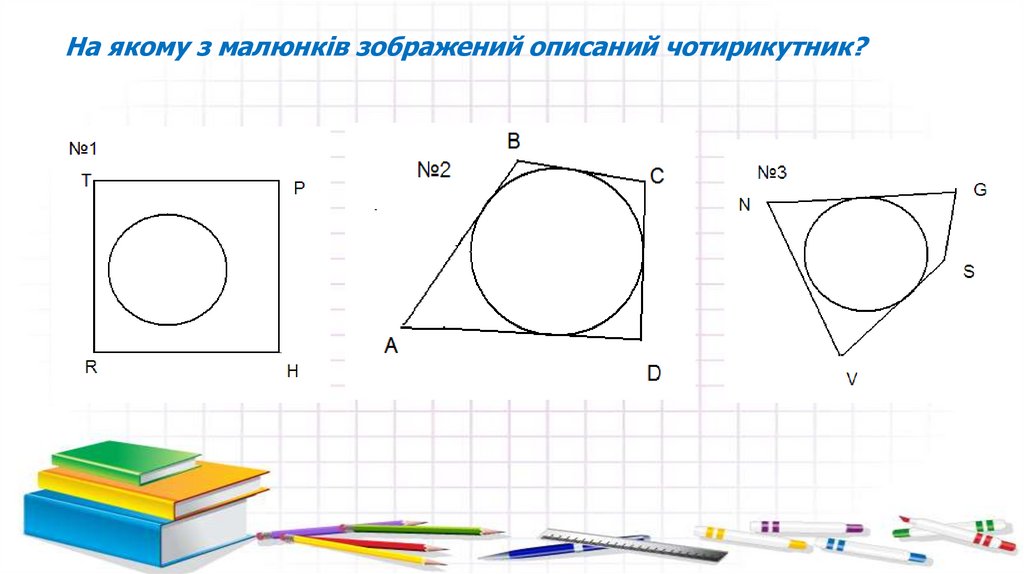
На якому з малюнків зображений описаний чотирикутник?

11.

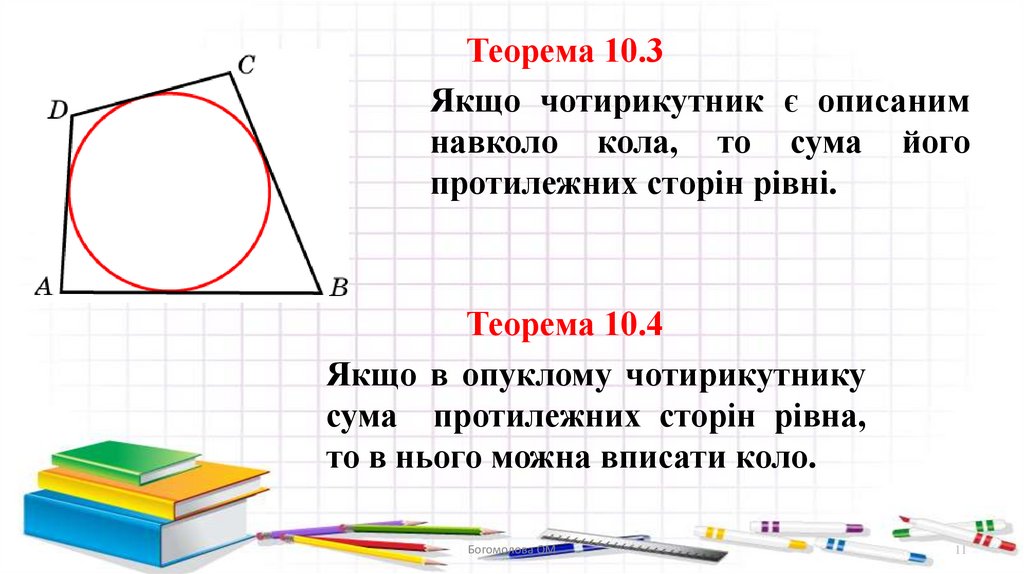
Теорема 10.3
Якщо чотирикутник є описаним
навколо кола, то сума його
протилежних сторін рівні.
Теорема 10.4
Якщо в опуклому чотирикутнику
сума протилежних сторін рівна,
то в нього можна вписати коло.
Богомолова ОМ
11

12.

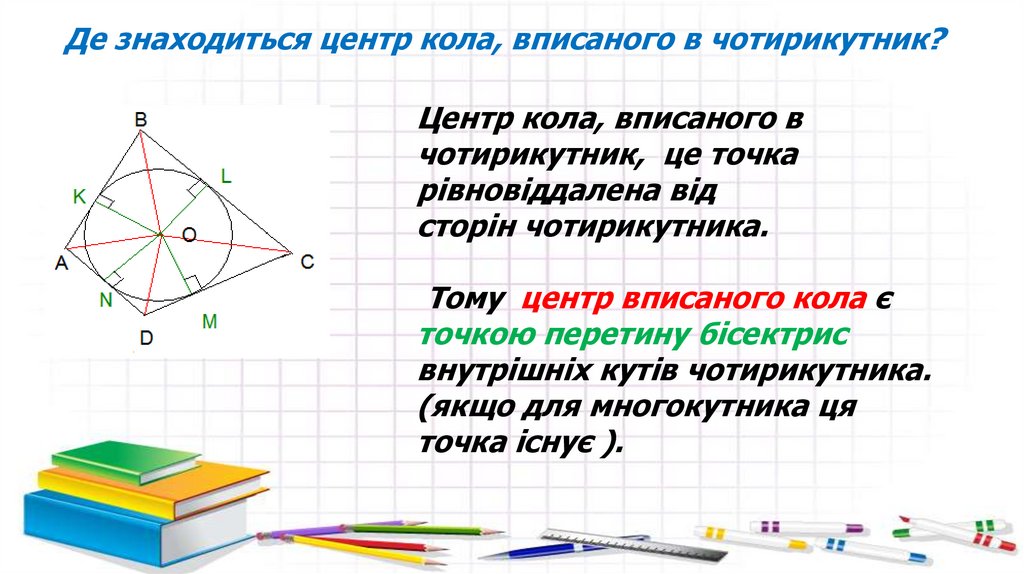
Де знаходиться центр кола, вписаного в чотирикутник?
Центр кола, вписаного в
чотирикутник, це точка
рівновіддалена від
сторін чотирикутника.
Тому центр вписаного кола є
точкою перетину бісектрис
внутрішніх кутів чотирикутника.
(якщо для многокутника ця
точка існує ).

13.

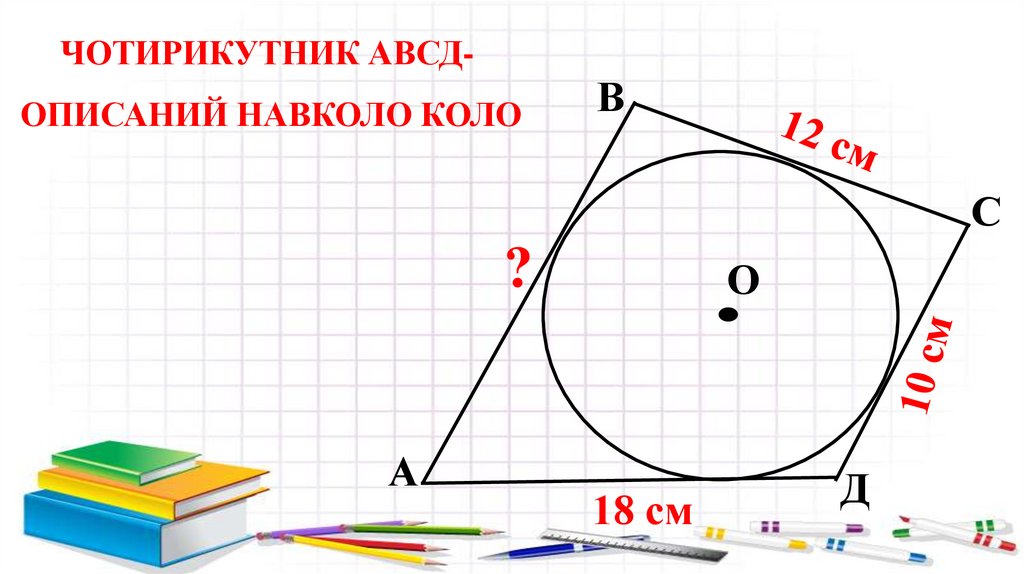
ЧОТИРИКУТНИК АВСД-
ОПИСАНИЙ НАВКОЛО КОЛО
В
С
?
А
О
18 см
Д

14.

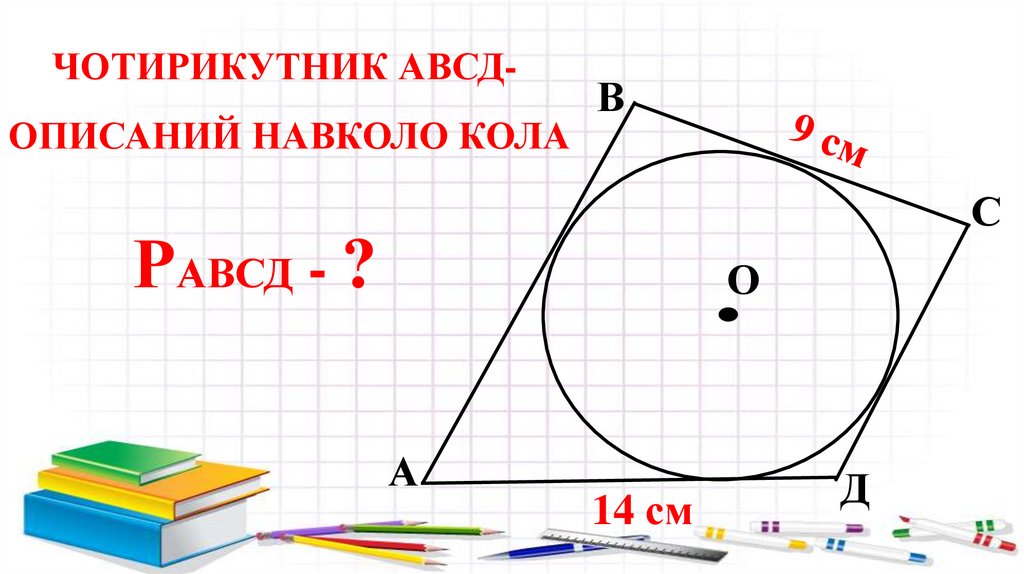
ЧОТИРИКУТНИК АВСДОПИСАНИЙ НАВКОЛО КОЛА
В
С
РАВСД - ?
О
А
14 см
Д

15.

В який паралелограм можна вписати коло?
З усіх паралелограмів
можна вписати коло
тільки в ромб.

16.

Середня лінія трапеції, у яку вписано коло, дорівнює 25 см. Знайти
периметр цієї трапеції.
С
В
25
А
Д

17.

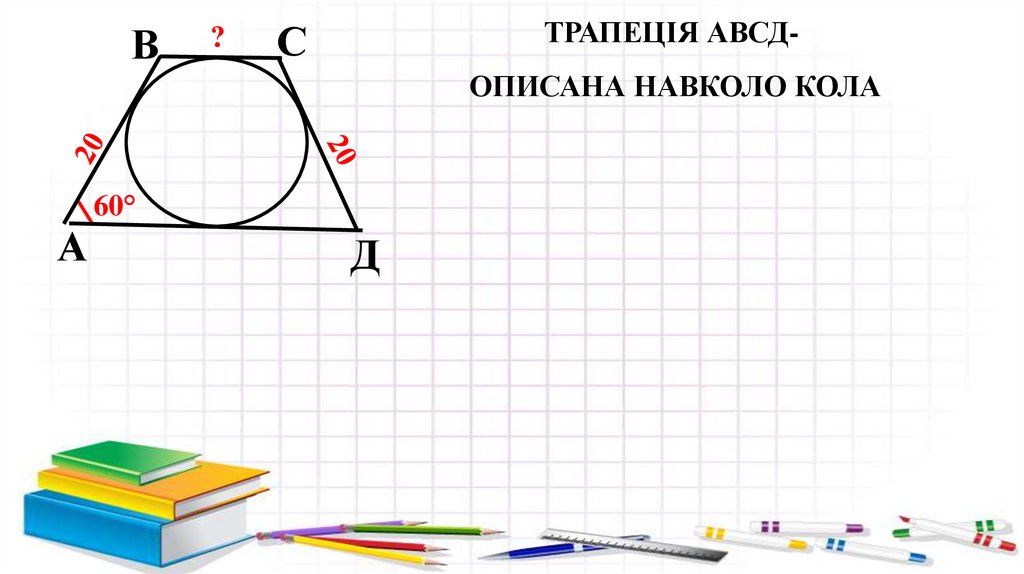
В
?
ТРАПЕЦІЯ АВСД-
С
ОПИСАНА НАВКОЛО КОЛА
60°
А
Д

18.

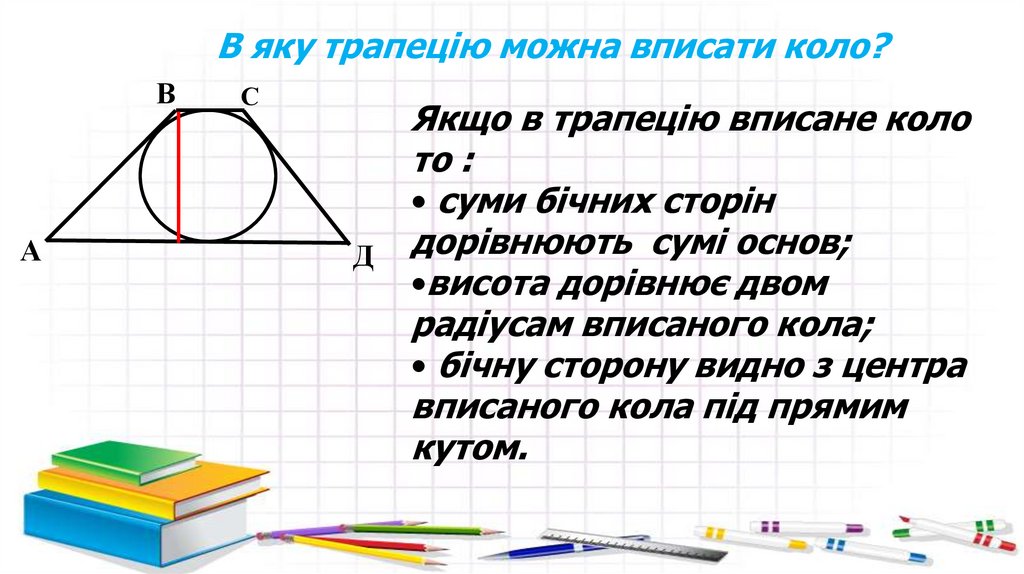
В яку трапецію можна вписати коло?
В
А
С
Д
Якщо в трапецію вписане коло
то :
• суми бічних сторін
дорівнюють сумі основ;
•висота дорівнює двом
радіусам вписаного кола;
• бічну сторону видно з центра
вписаного кола під прямим
кутом.

19.

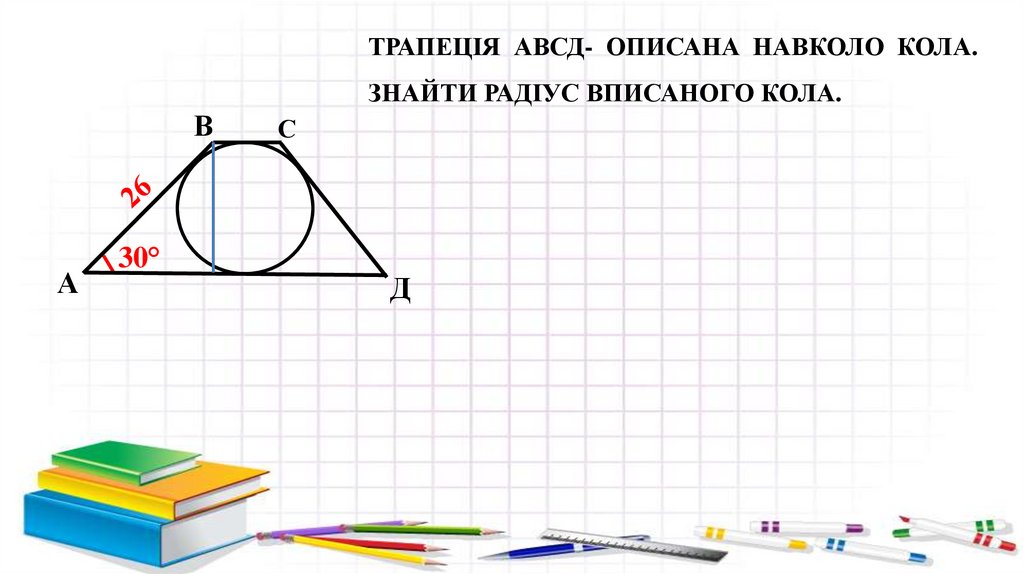
ТРАПЕЦІЯ АВСД- ОПИСАНА НАВКОЛО КОЛА.
ЗНАЙТИ РАДІУС ВПИСАНОГО КОЛА.
В
А
30°
С
Д

20.

21.

22.

Квадрат

23.

К
В
R
R
R
О
R
ВПИСАНИЙ
ЧОТИРИКУТНИК
С
С
M
L
А
УМОВА: ∠В + ∠С = ∠К + ∠А =