Бондаренко_067241_ЛР2

1.

Лабораторная работа ПЭ2
ПОДБОР АППРОКСИМИРУЮЩИХ ФУНКЦИЙ.
РАСЧЕТ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ
ПАРАМЕТРОВ ВЫБРАННОЙ
АППРОКСИМИРУЮЩЕЙ ФУНКЦИИ
Выполнил:
Магистрант гр.067241
Бондаренко М.И.

2.

Цель работы:
Изучение методов идентификации формы экспериментальной
зависимости и ее математического описания.
Освоение прикладного программного обеспечения для визуализации
экспериментальных данных.
Построение графиков заданных экспериментальных зависимостей.
Подбор аппроксимирующих функций заданных экспериментальных
зависимостей.

3.

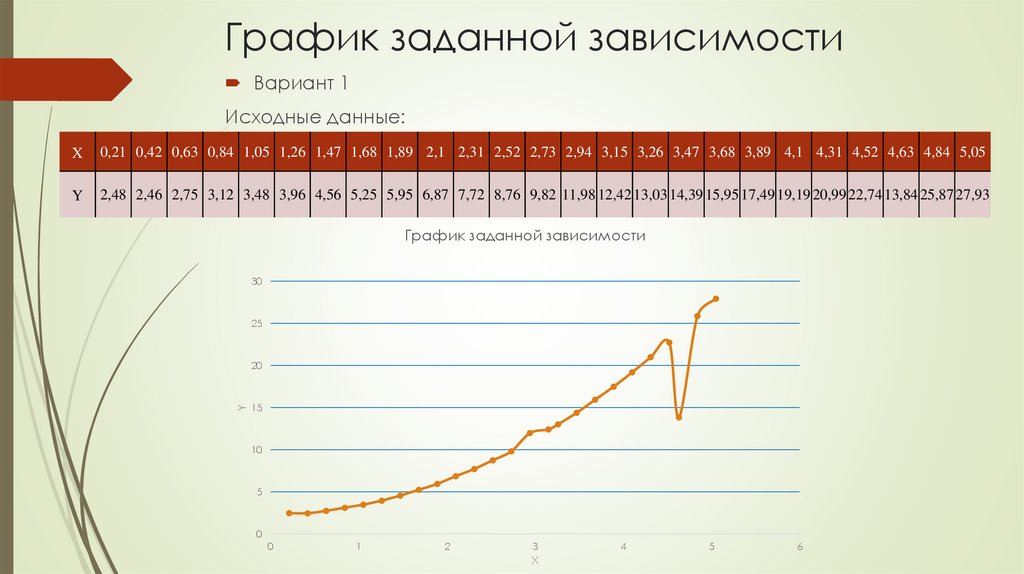
График заданной зависимости
Вариант 1
Исходные данные:
X
0,21 0,42 0,63 0,84 1,05 1,26 1,47 1,68 1,89 2,1 2,31 2,52 2,73 2,94 3,15 3,26 3,47 3,68 3,89 4,1 4,31 4,52 4,63 4,84 5,05
Y
2,48 2,46 2,75 3,12 3,48 3,96 4,56 5,25 5,95 6,87 7,72 8,76 9,82 11,98 12,42 13,03 14,39 15,95 17,49 19,19 20,99 22,74 13,84 25,87 27,93
График заданной зависимости
30
25
Y
20
15
10
5
0
0
1
2
3
X
4
5
6

4.

Аппроксимирующая функция y = axn
lgx
lgy
lgx
lgy
-0,67778071
0,3944517
0,46834733
1,0784568
-0,37675071
0,3909351
0,498310554
1,0941216
-0,20065945
0,4393327
0,5132176
1,1149444
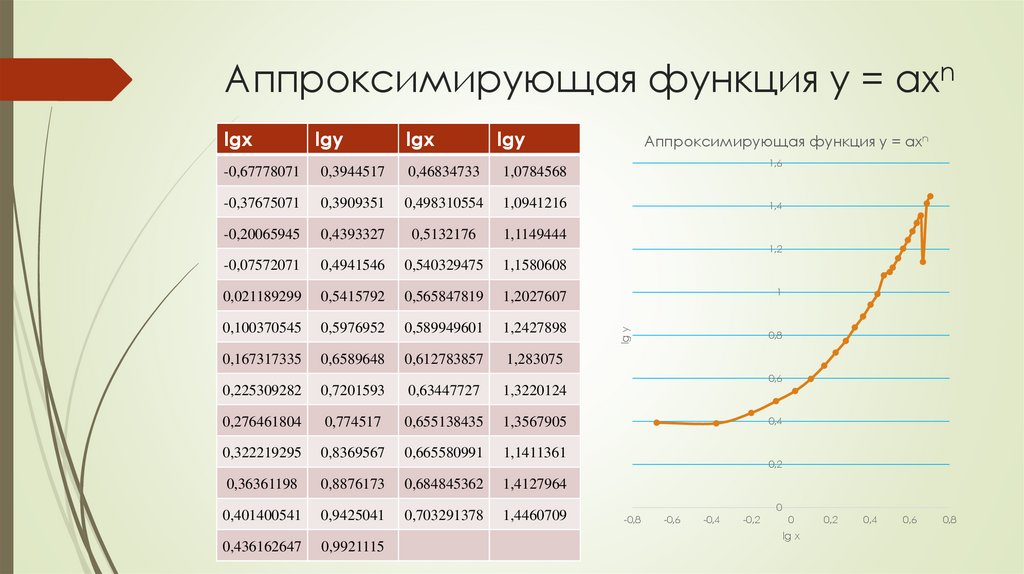
Аппроксимирующая функция y = axn
1,6
1,4
1,2
0,4941546
0,540329475
1,1580608
0,021189299
0,5415792
0,565847819
1,2027607
0,100370545
0,5976952
0,589949601
1,2427898
0,167317335
0,6589648
0,612783857
1,283075
0,225309282
0,7201593
0,63447727
1,3220124
0,276461804
0,774517
0,655138435
1,3567905
0,322219295
0,8369567
0,665580991
1,1411361
0,36361198
0,8876173
0,684845362
1,4127964
0,401400541
0,9425041
0,703291378
1,4460709
0,436162647
0,9921115
1
lg y
-0,07572071
0,8
0,6
0,4
0,2
0
-0,8
-0,6
-0,4
-0,2
0
lg x
0,2
0,4
0,6
0,8

5.

Вывод
Экспериментальные точки не лежат вдоль прямой, следовательно
модель в виде показательной функции не является адекватной.

6.

Аппроксимирующая функция y = aebx
x
ln y
x
ln y
0,21
0,9082586
2,94
2,4832386
0,42
0,9001613
3,15
2,5193081
0,63
1,0116009
3,26
2,5672544
0,84
1,137833
3,47
2,6665335
1,05
1,2470323
3,68
2,7694588
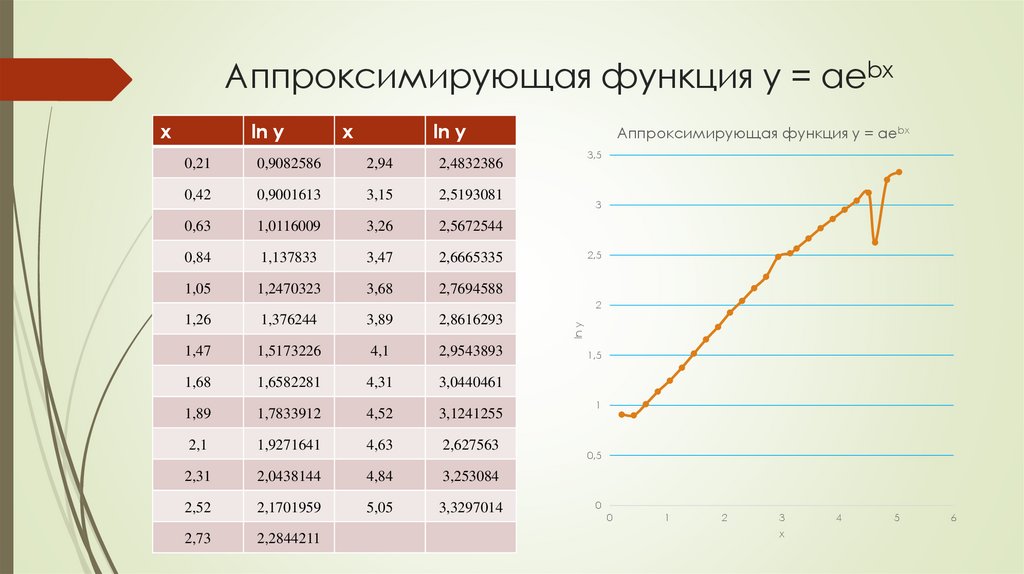
Аппроксимирующая функция y = aebx
3,5
3
2,5
1,26
1,376244
3,89
2,8616293
1,47
1,5173226
4,1
2,9543893
1,68
1,6582281
4,31
3,0440461
1,89
1,7833912
4,52
3,1241255
2,1
1,9271641
4,63
2,627563
2,31
2,0438144
4,84
3,253084
2,52
2,1701959
5,05
3,3297014
2,73
2,2844211
ln y
2
1,5
1
0,5
0
0
1
2
3
x
4
5
6

7.

Выводы
Поле экспериментальных точек группируется относительно прямой
линии, а значит модель в виде показательной функции можно выбрать
окончательно;
Точку (4,63; 2,63) можно считать погрешностью измерения;
Параметры модели:
a = 0,787 (пересечение с осью ln y)
b = 0,515 (наклон оси к прямой х)

8.

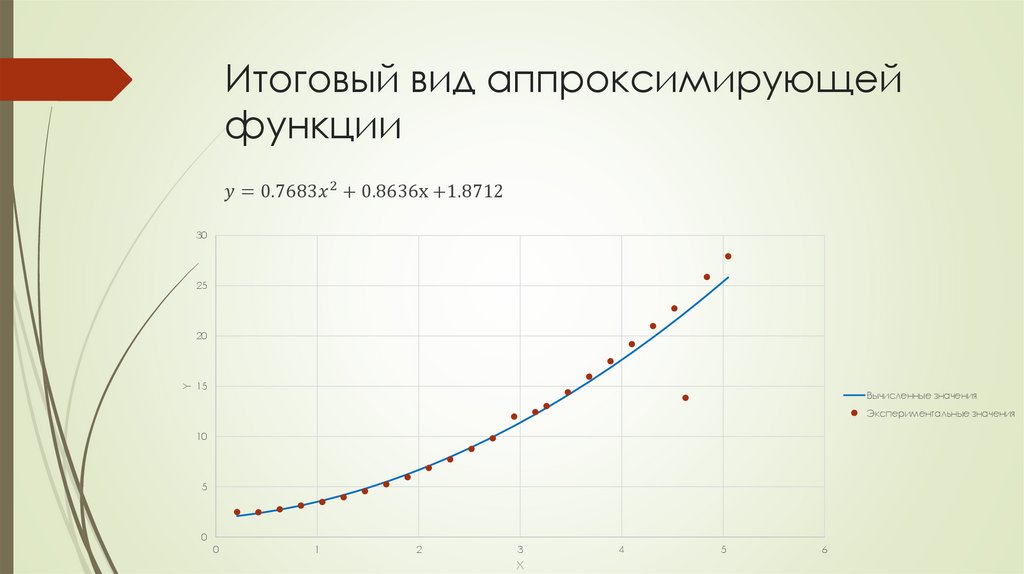
Аппроксимирующая функция
y = ax2 + bx + c
Составим таблицу вспомогательных величин:
i
xi
yi
x i2
x i3
x i4
x iy i
x i2 y i
1
0,21
2,48
0,0441
0,009261
0,001945
0,5208
0,109368
2
0,42
2,46
0,1764
0,074088
0,031117
1,0332
0,433944
…
…
…
…
…
…
…
…
25
5,05
27,93
25,5025 128,787625 650,3775
141,0465
712,2848
sum
66,95
283
232,2085 901,235975 3720,815 1018,2182 4071,465

9.

Система линейных уравнений