теорема пифагора

1.

Тема: Теорема Пифагора. Решение задач
Цель: Формирование знаний на тему решение задач
с теоремой Пифагора
Задача: Научиться решать задачи с теоремой
Пифагора

2.

Задача 1: высота BH равнобедренного
треугольника ABC
равна 20 см, а его основание AC — 30 см.
Найдите боковую сторону AB данного
треугольника .

3.

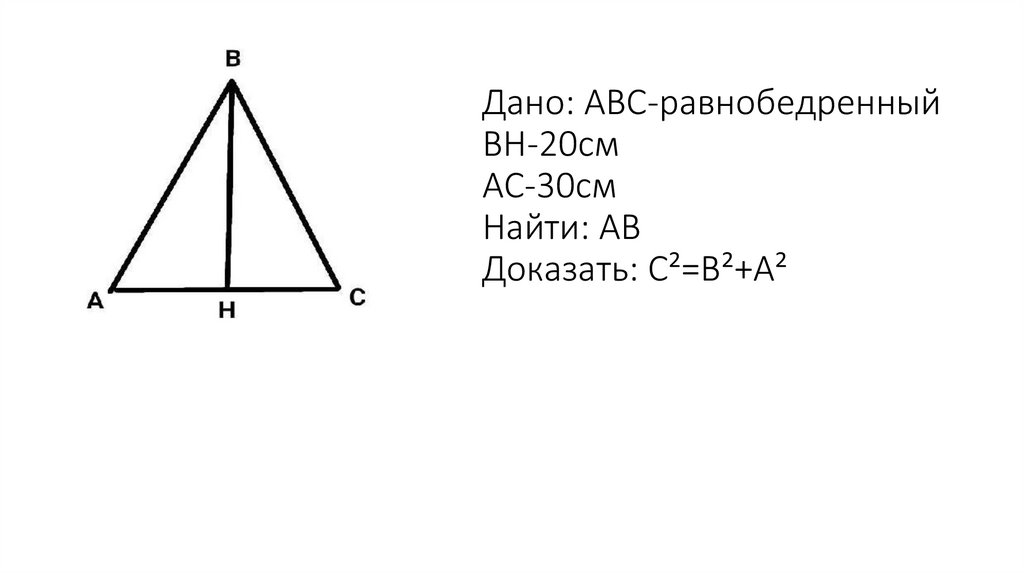
Дано: ABC-равнобедренный
BH-20см
AC-30см
Найти: AB
Доказать: C²=B²+A²

4.

Доказательство:
Т.к. треугольник равнобедренный высота BH является и медианой
треугольник=> она делит AC на равные отрезки AH и CH
Тогда: AH=CH=AC:2=3
30:2=15см
ABM-прямоугольный
AB²=AH²+BH²=20²+15²=400+225=625
AB= 625=25см
Ответ: AB=25см Доказано

5.

Задача 2: в равнобокой трапеции ABCD основания
равны BC=8 см, AD=14 см, высота трапеции BH=4
см. Найдите боковую сторону трапеции CD.

6.

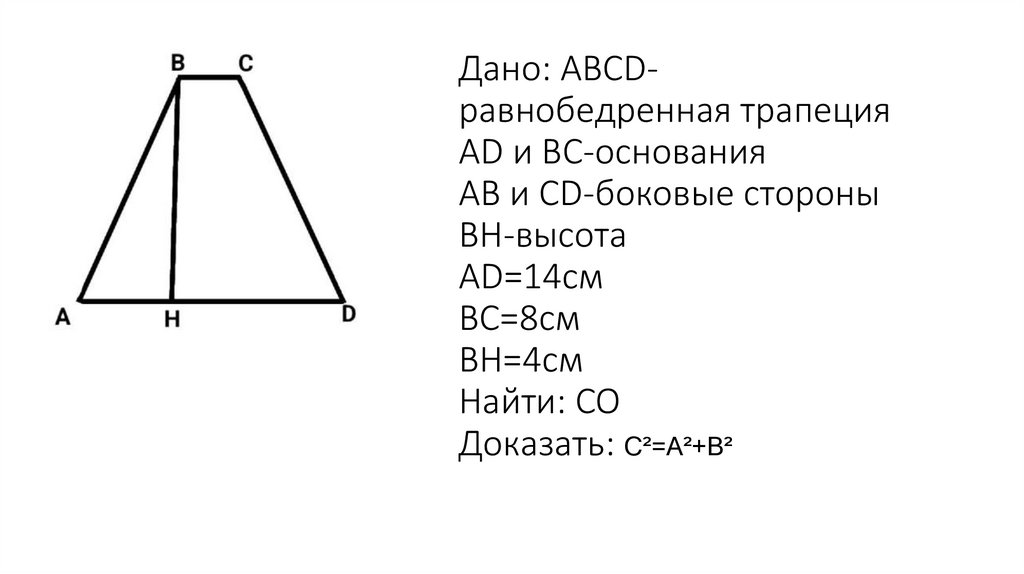
Дано: ABCDравнобедренная трапеция
AD и BC-основания
AB и CD-боковые стороны
BH-высота
AD=14см
BC=8см
BH=4см
Найти: CO
Доказать: С²=А²+В²

7.

Доказательство:
По теореме Пифагора из углс АВН найдём гипотенузу АВ
АН= (14-8):2= 3 см (по условию трапеция равнобокая)
АВ²=4²+3²
АВ²= 16+9= 25 см
АВ= Корень25= 5 см
АВ=СD=5 см
Ответ: 5 см. Доказано.

8.

Задача 3: в ромбе ABCD, длинная диагональ AC
составляет 48 см, короткая диагональ BD составляет
14 см. Найдите сторону АВ.

9.

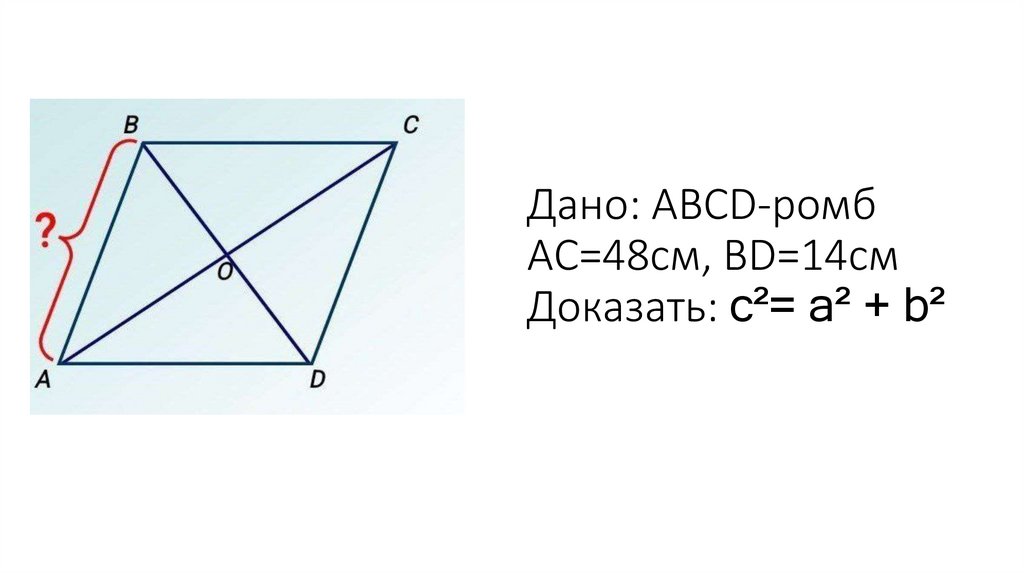
Дано: ABCD-ромб
AC=48см, BD=14см
Доказать: c²= a² + b²

10.

Доказательство:
Половины диагоналей — катеты треугольника:
1) 14 : 2 = 7 см;
48 : 2 = 24 см.
Применим теорему Пифагора для нахождения гипотенузы:
2) c²= a² + b²;
c = √(24² + 7²) = √(576 + 49) = √625 = 25 см.
Ответ: AB=25 см.

11.

Вывод: мы научились решать задачи с
теоремой Пифагора