Практики теорема Пифагора

1. «Практики» Приступив к выполнению проекта, мы поставили перед собой

задачи:
Научиться решать задачи с применением
теоремы Пифагора
Отобрать практические задачи, решаемые
с применением теоремы Пифагора
Привести примеры занимательных и
исторических задач

2.

Рассмотрим примеры задач, в которых при
решении применяется теорема Пифагора.

3.

Применение теоремы Пифагора
к решению прямоугольных
треугольников:
1. Находим гипотенузу по известным
катетам
2. Находим катет по гипотенузе и
второму катету

4.

Находим гипотенузу по известным катетам
А
Дано:
b
ABC-прямоугольный
а ; в - катеты
а=6
в =8
Найти: с (гипотенуза)
c
Решение: По теореме Пифагора
В
С
a
с2 = а2 + в2
с2 = 62 + 82
с2 = 36 + 64
с2 = 100
с = 100;
с = 10;
с = - 100
с = - 10 (не удовлетворяет
условиям задачи)
ОТВЕТ: с = 10

5. Находим катет по гипотенузе и второму катету (самостоятельно в парах)

Находим катет по
гипотенузе и второму катету
А
(самостоятельно в парах)
Дано:
c
b
С
АВС – прямоугольный
в = 6 (катет)
с = 10 (гипотенуза)
Найти: а
a
B
(

6. Находим катет по гипотенузе и второму катету

А
Дано:
c
b
С
АВС – прямоугольный
в = 6 (катет)
с = 10 (гипотенуза)
Найти: а
a
B
Решение: По теореме Пифагора
с2 = а2 + в2
а2 = с2 – в2
а2 = 102 – 62
а2 = 100 – 36
а2 = 64
а = 64
a=8
ОТВЕТ: а = 8
a = - 64 (не удовлетворяет
условиям задачи)
a=-8

7.

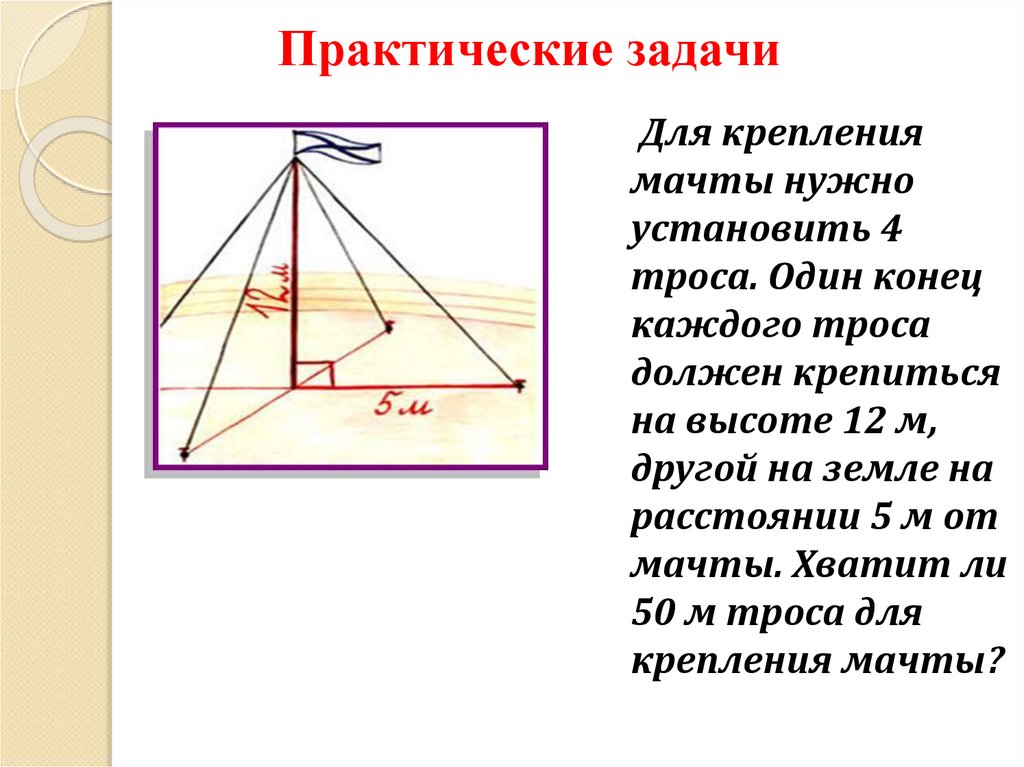
Практические задачи
Для крепления
мачты нужно
установить 4
троса. Один конец
каждого троса
должен крепиться
на высоте 12 м,
другой на земле на
расстоянии 5 м от
мачты. Хватит ли
50 м троса для
крепления мачты?

8.

12 м
А
С 5М
В
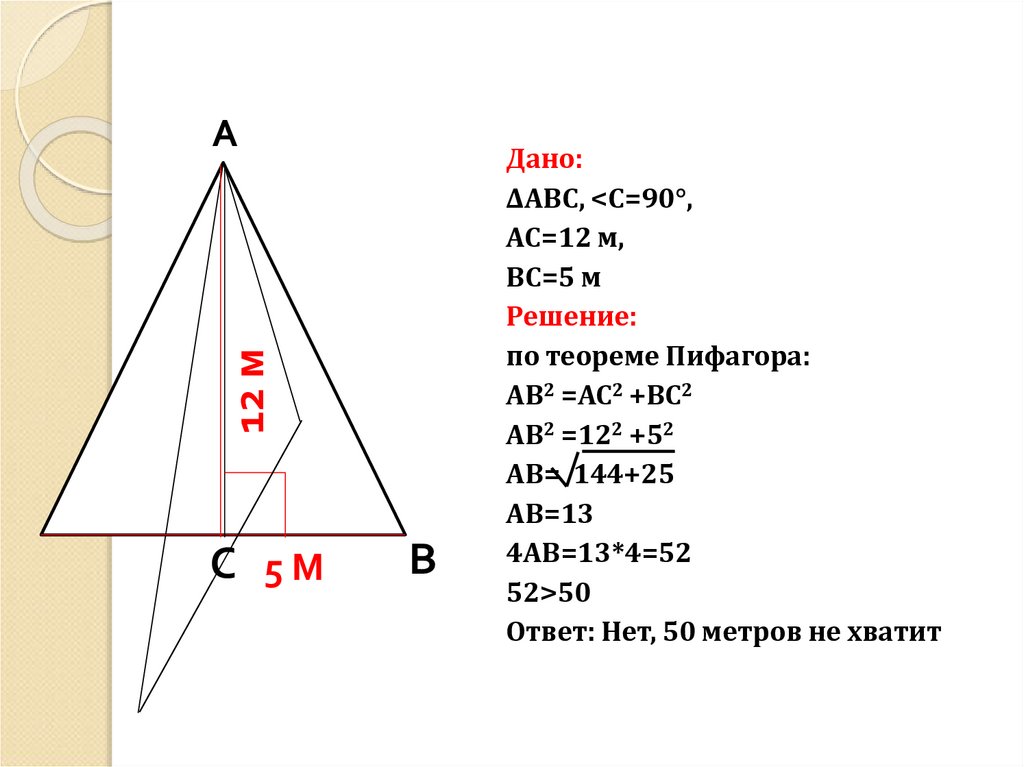
Дано:
ΔАBC, <С=90°,
АС=12 м,
ВС=5 м
Решение:
по теореме Пифагора:
АВ2 =АС2 +ВС2
АВ2 =122 +52
АВ= 144+25
АВ=13
4АВ=13*4=52
52>50
Ответ: Нет, 50 метров не хватит

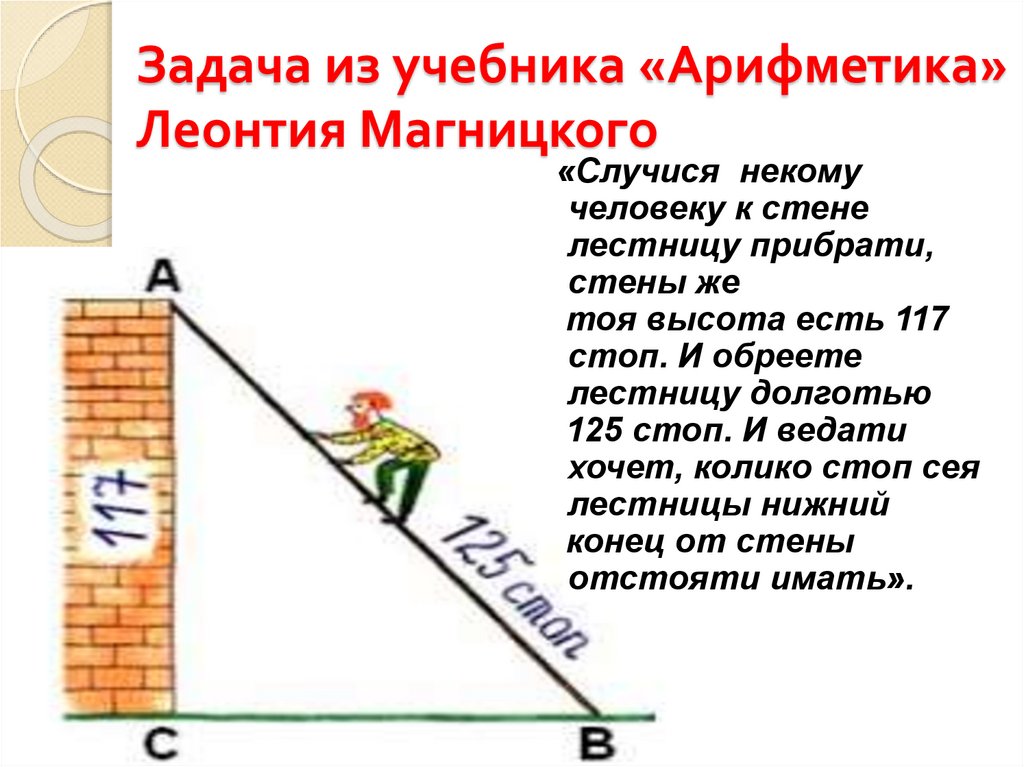
9. Задача из учебника «Арифметика» Леонтия Магницкого

«Случися некому
человеку к стене
лестницу прибрати,
стены же
тоя высота есть 117
стоп. И обреете
лестницу долготью
125 стоп. И ведати
хочет, колико стоп сея
лестницы нижний
конец от стены
отстояти имать».

10.

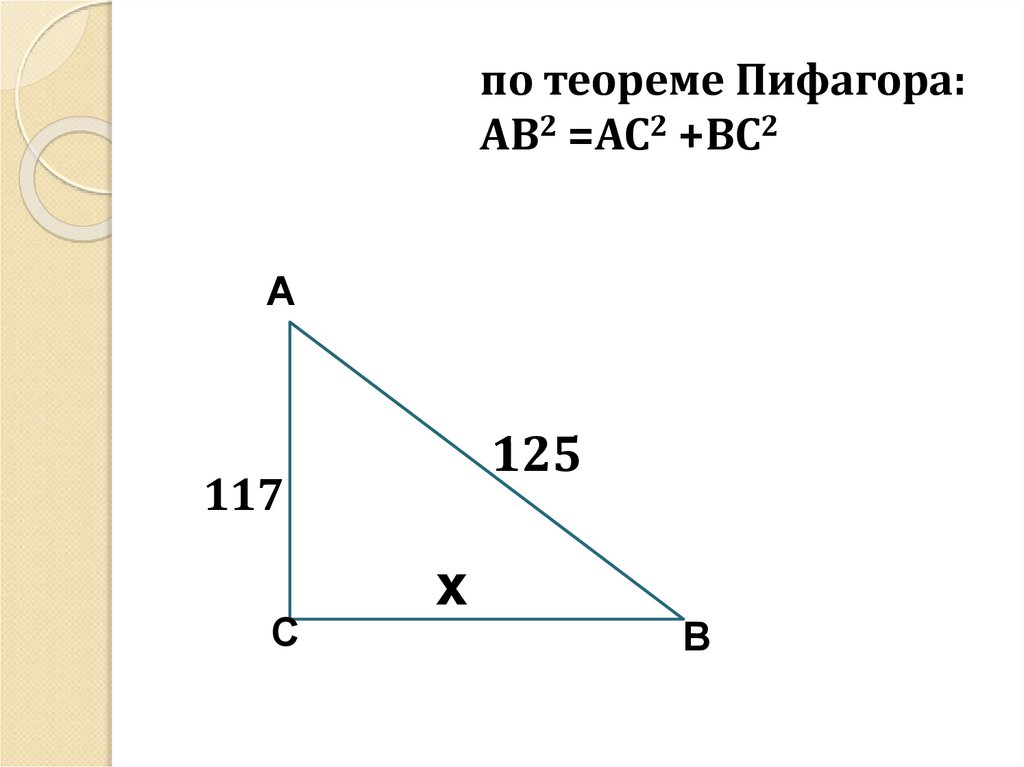
по теореме Пифагора:
АВ2 =АС2 +ВС2
А
125
117
С
х
В

11.

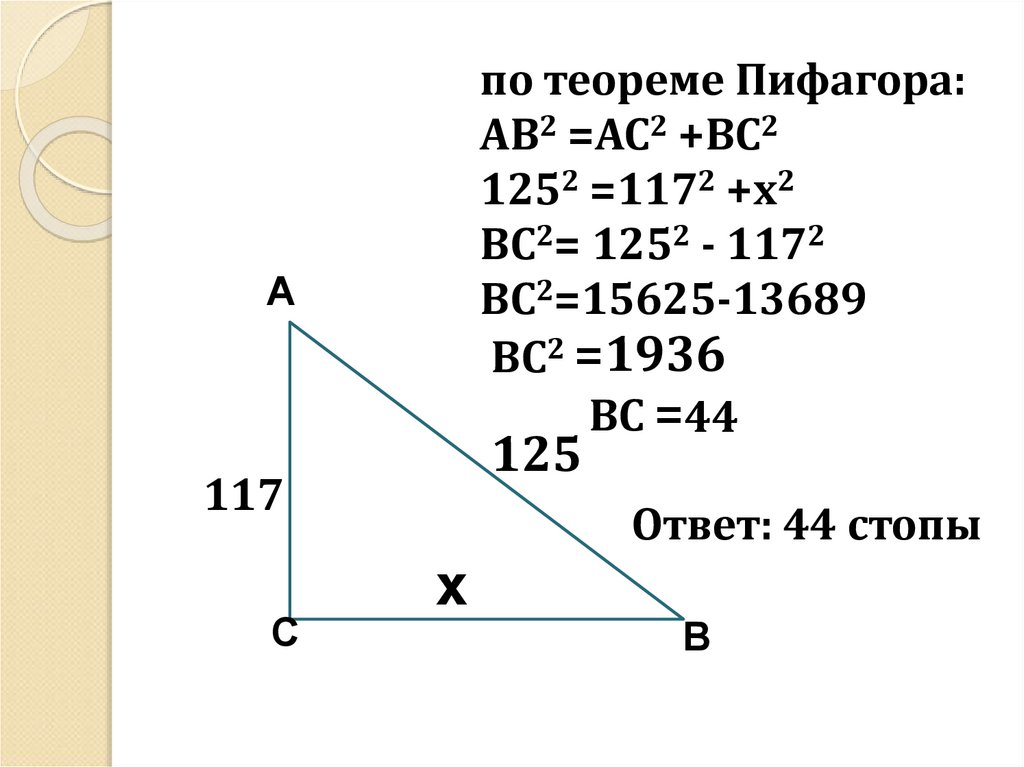
по теореме Пифагора:
АВ2 =АС2 +ВС2
1252 =1172 +х2
ВС2= 1252 - 1172
ВС2=15625-13689
ВС2 =1936
ВС =44
А
125
117
С
Ответ: 44 стопы
х
В

12. Задача землемеров

Землемеры Древнего
Египта для построения
прямого угла использовали бечёвку, разделённую узлами на 12 равных
частей.
Треугольники со сторонами 3;4;5 называют
египетскими треугольниками

13.

Прямоугольные треугольники, у
которых длины сторон
выражаются целыми числами,
называются пифагоровыми
треугольниками.

14.

За 8 веков до нашей эры эта теорема
была хорошо известна индийцам под
названием «правила веревки»,
использовалась ими для построения
алтарей, которые по священному
предписанию должны иметь строгую
геометрическую форму,
ориентированную относительно четырех
сторон горизонта.
О том, что треугольник со сторонами
3; 4 и 5 есть прямоугольный, знали за
2000 лет до н.э. египтяне, которые
использовали этот факт в определении
прямых углов при строительстве зданий.

15.

Теорема Пифагора встречается в разных
областях наук, не только в геометрии, но и в
физике, астрономии, архитектуре, технике,
строительстве (окна, молниеотводы, крыши), в
народном хозяйстве, на рынке мобильной связи
при строительстве вышек.

16. Теорема Пифагора в природе

17. «Ворона»

18. «Букет»

19. «Лужайка»

20. Пальмы

21. Ночь

22. Вывод группы практиков:

Благодаря тому, что теорема Пифагора
позволяет находить длину гипотенузы,
не измеряя ее непосредственно, она как
бы открывает путь с прямой на
плоскость, с плоскости в трехмерное
пространство и дальше – в
многомерные пространства. Этим
определяется ее исключительная
важность для геометрии и математики
в целом