Степенная и показательная функции (1)

1.

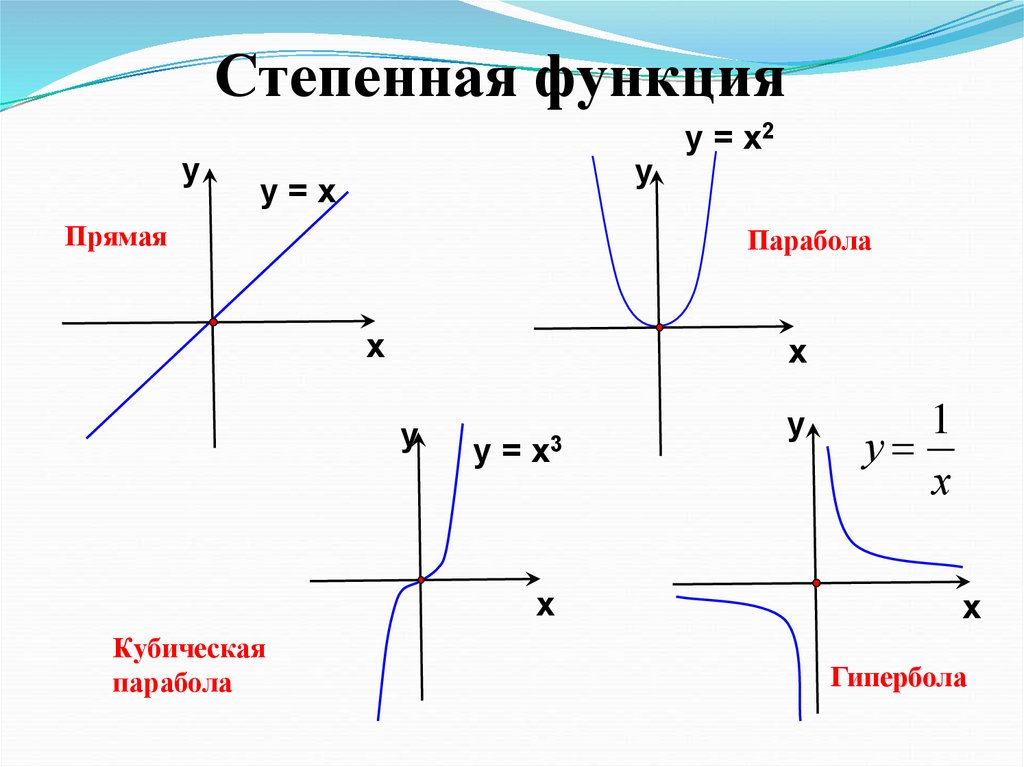
Степенная функция
у
у
у=х
Прямая
Парабола
х
х
у
у = х3
х
Кубическая
парабола
у = х2
у
1
у
х
х
Гипербола

2.

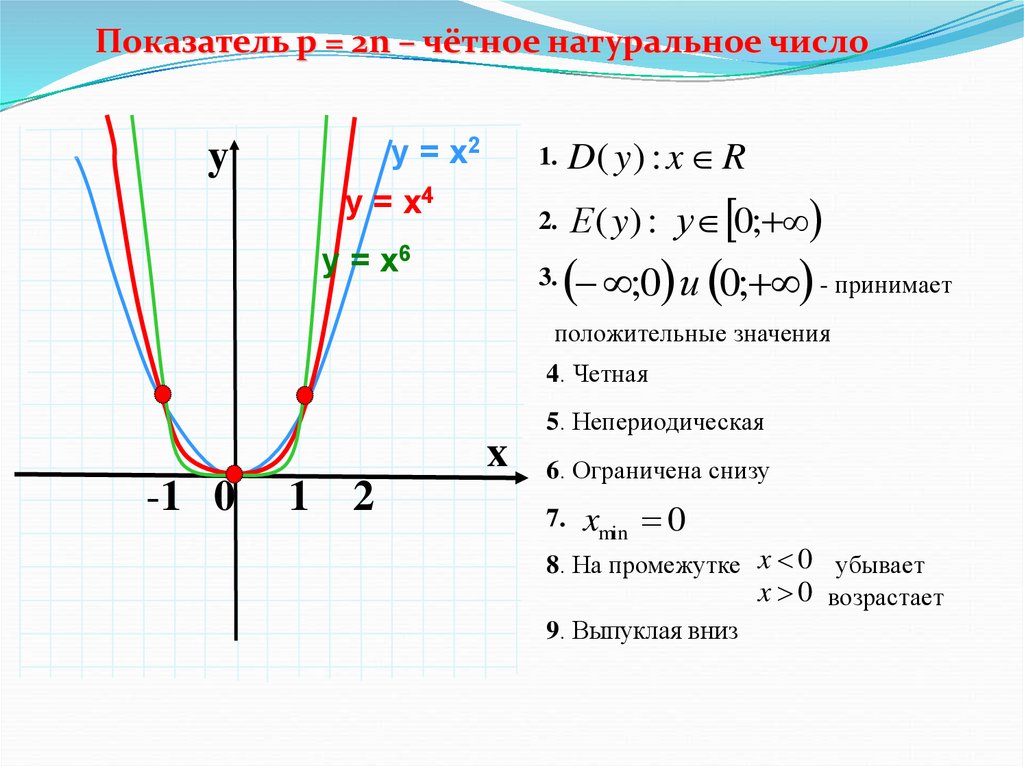
Показатель p = 2n – чётное натуральное число
1. D ( y ) : x R
у = х2
у = х4
y
2. Е ( y) :
у = х6
у 0;
0; - принимает
3. ;0 и
положительные значения
4. Четная
5. Непериодическая
x
-1 0
1
2
6. Ограничена снизу
7. x
min
0
8. На промежутке x 0 убывает
x 0 возрастает
9. Выпуклая вниз

3.

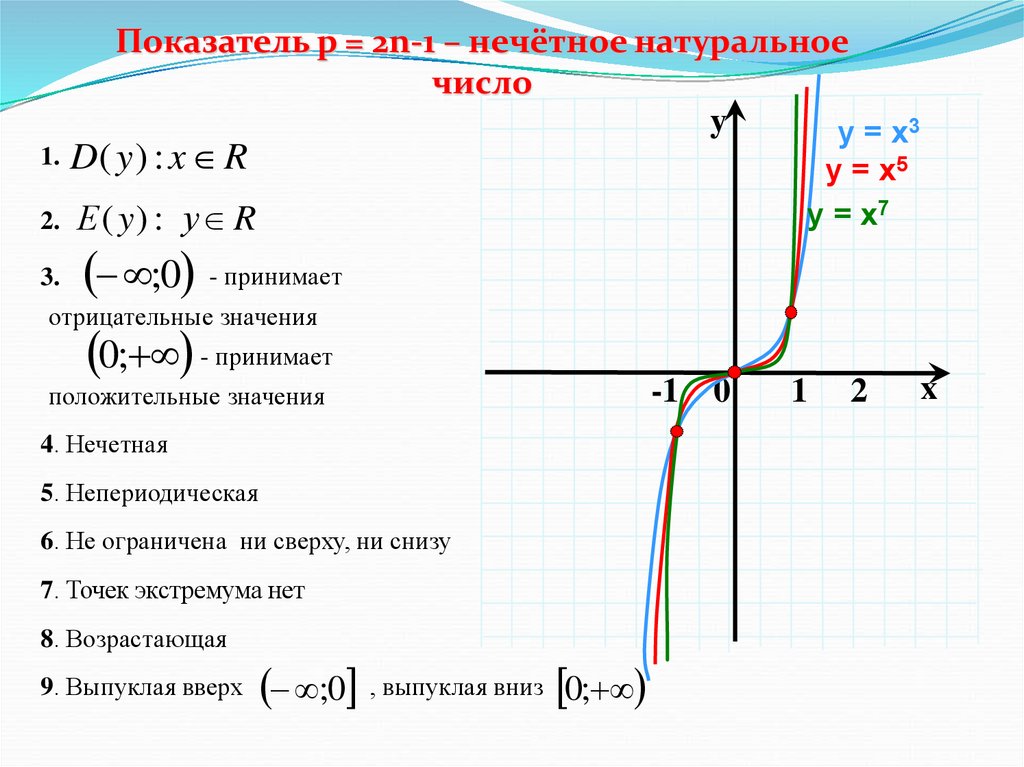
Показатель p = 2n-1 – нечётное натуральное
число
y
у = х3
1. D ( y ) : x R
2. Е ( y ) :
3.
у = х5
у = х7
у R
;0 - принимает
отрицательные значения
0; - принимает
положительные значения
4. Нечетная
5. Непериодическая
6. Не ограничена ни сверху, ни снизу
7. Точек экстремума нет
8. Возрастающая
9. Выпуклая вверх
;0 , выпуклая вниз 0;
-1
0
1
2
x

4.

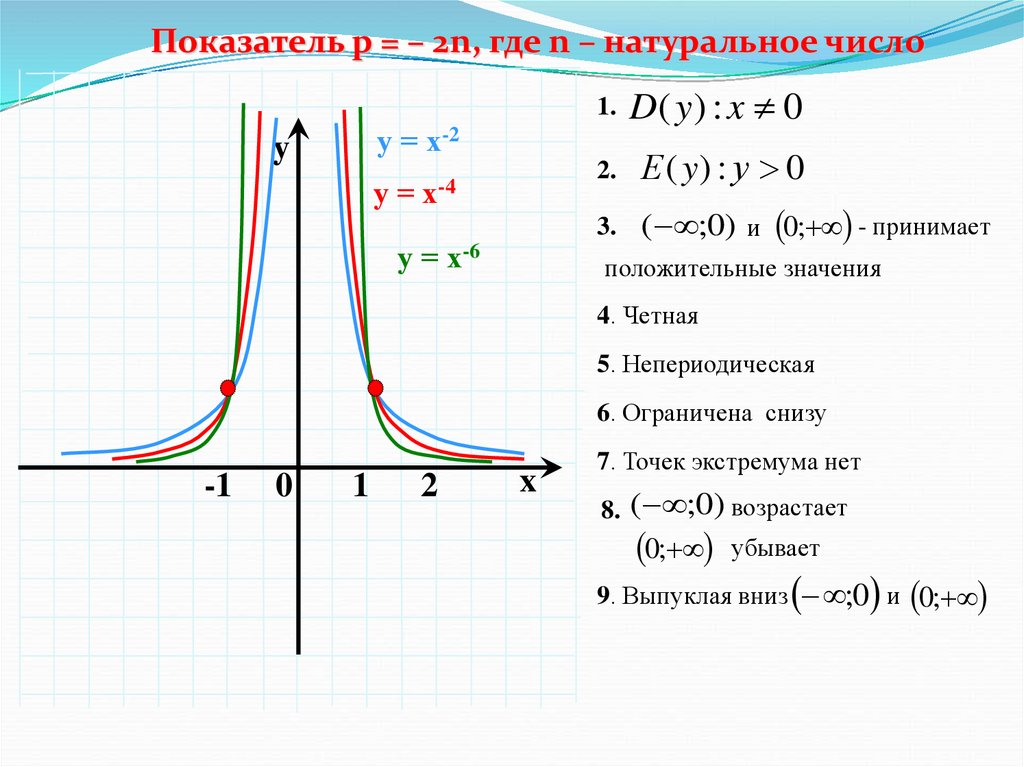
Показатель р = – 2n, где n – натуральное число
1. D ( y ) : x 0
у = х-2
y
у = х-4
у = х-6
2.
Е ( y) : у 0
3.
( ;0) и 0; - принимает
положительные значения
4. Четная
5. Непериодическая
6. Ограничена снизу
-1
0
1
2
x
7. Точек экстремума нет
8. ( ;0) возрастает
0; убывает
9. Выпуклая вниз ;0 и 0;

5.

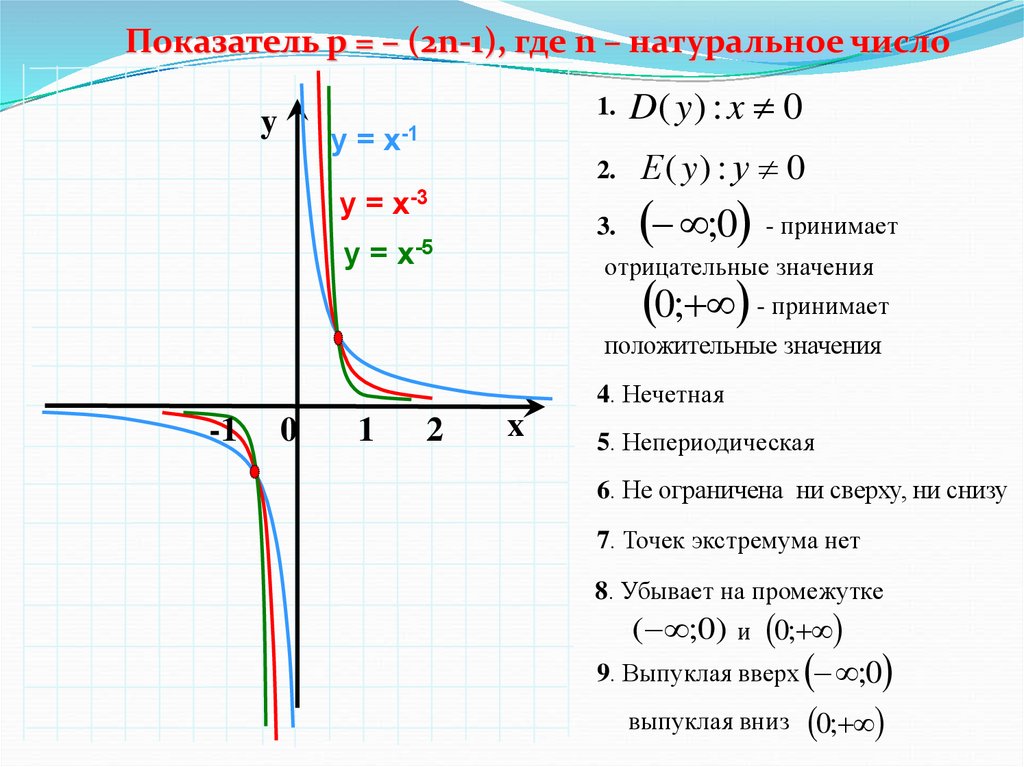
Показатель р = – (2n-1), где n – натуральное число
y
1. D ( y ) : x 0
у = х-1
2.
у = х-3
3.
у = х-5
Е ( y) : у 0
;0 - принимает
отрицательные значения
0; - принимает
положительные значения
4. Нечетная
-1
0
1
2
x
5. Непериодическая
6. Не ограничена ни сверху, ни снизу
7. Точек экстремума нет
8. Убывает на промежутке
( ;0) и 0;
9. Выпуклая вверх ;0
выпуклая вниз
0;

6.

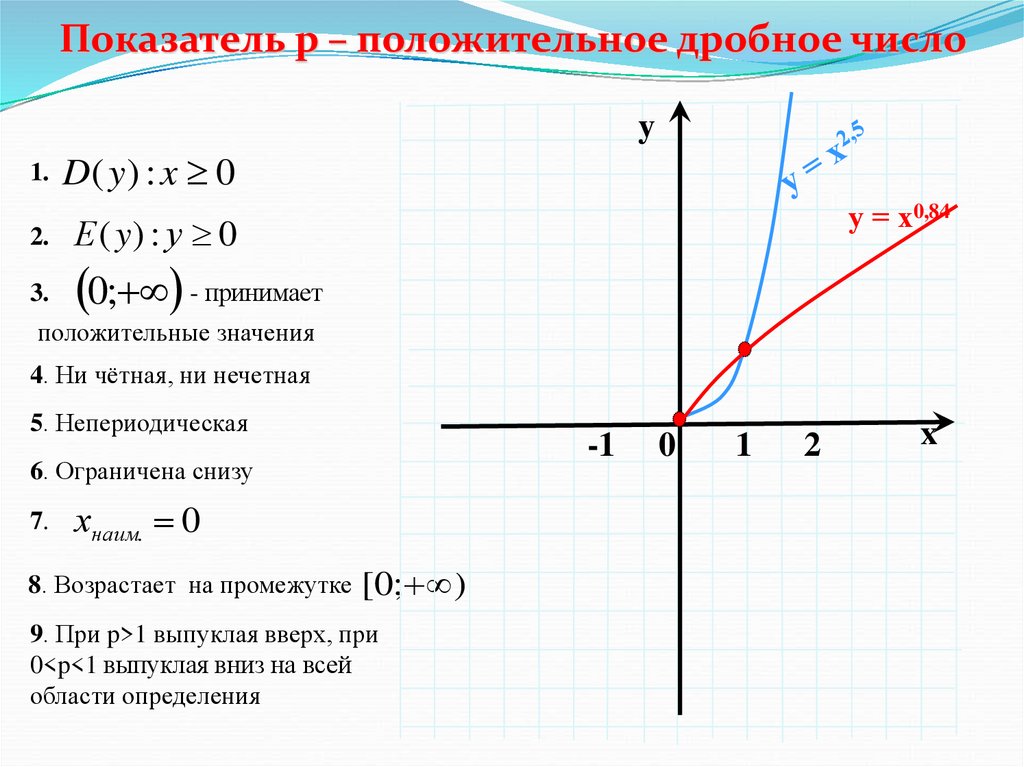
Показатель р – положительное дробное число
y
1. D ( y ) : x 0
2.
3.
у = х0,84
Е ( y) : у 0
0; - принимает
положительные значения
4. Ни чётная, ни нечетная
5. Непериодическая
6. Ограничена снизу
7.
хнаим. 0
8. Возрастает на промежутке [0; )
9. При p>1 выпуклая вверх, при
0<p<1 выпуклая вниз на всей
области определения
-1
0
1
2
x

7.

Преобразования
графиков
степенных функций

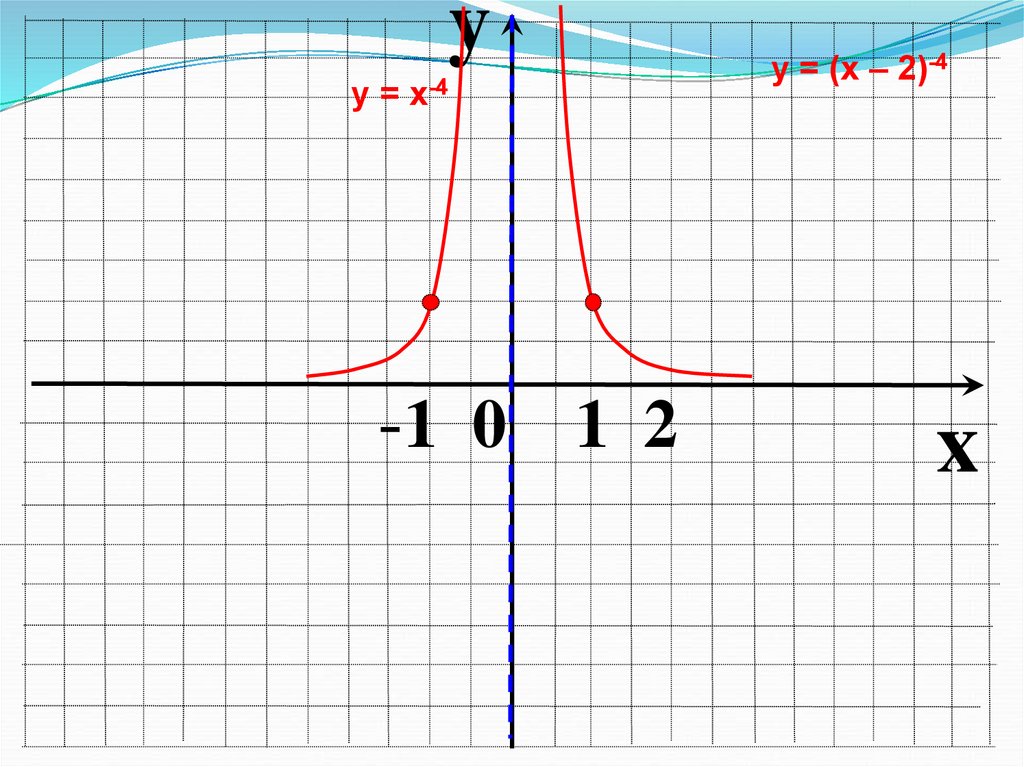
8.

y
у = х-4
-1 0 1 2
у = (х – 2)-4
x

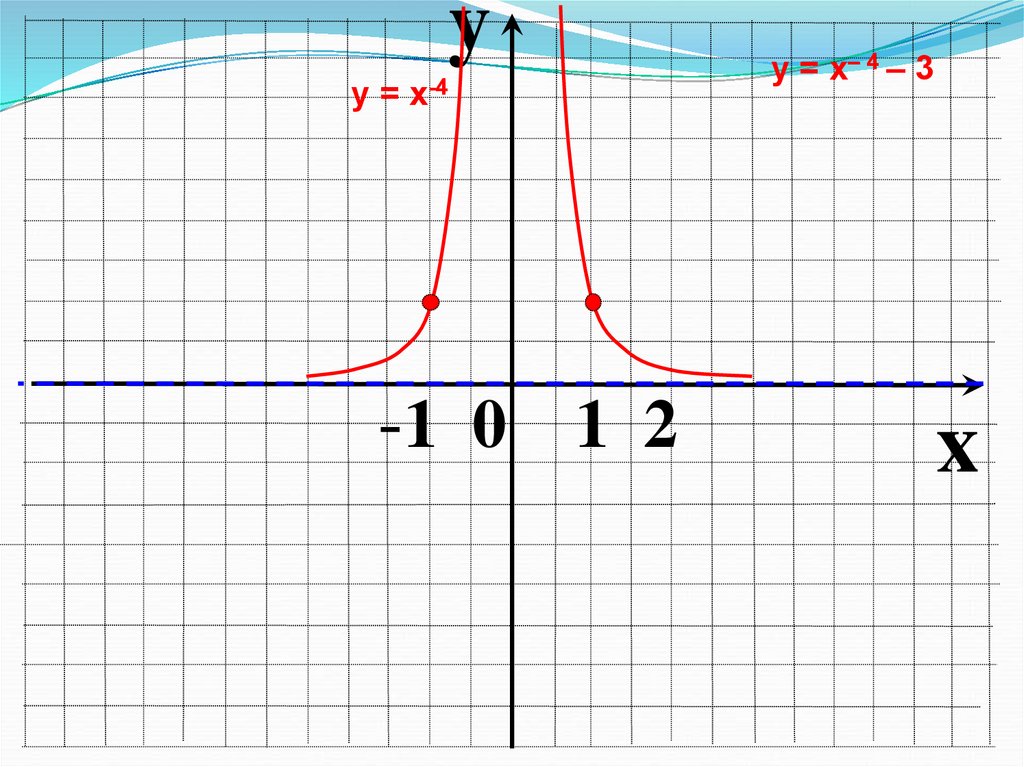
9.

y
у = х-4
-1 0 1 2
у = х– 4 – 3
x

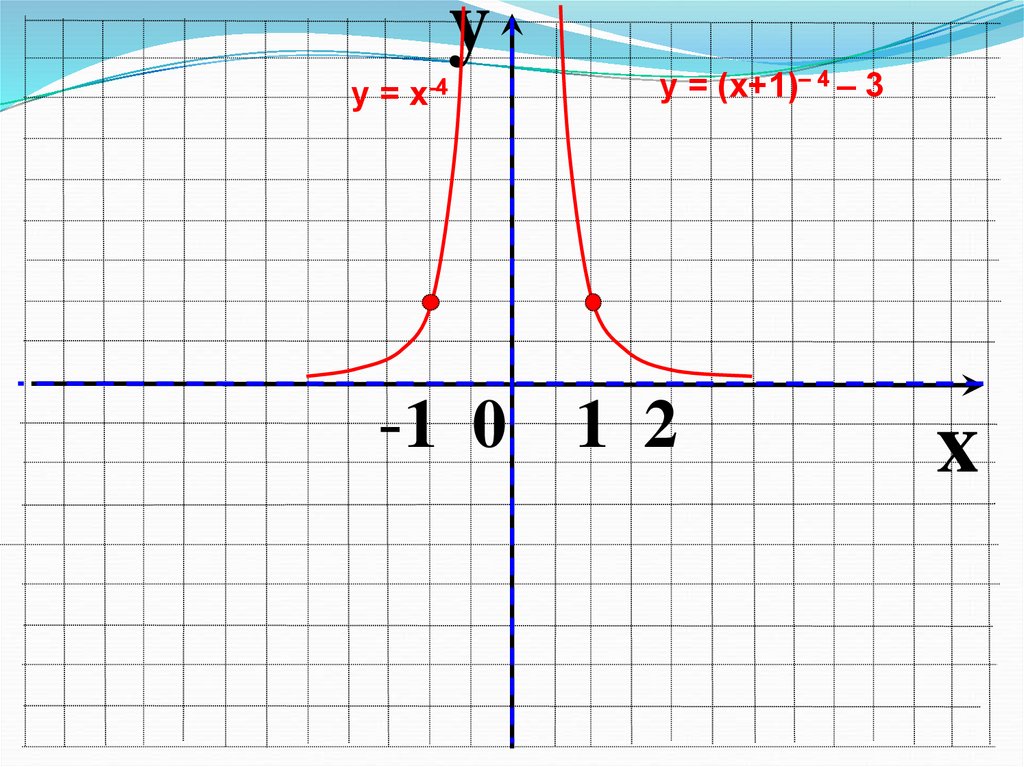
10.

y
у = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x

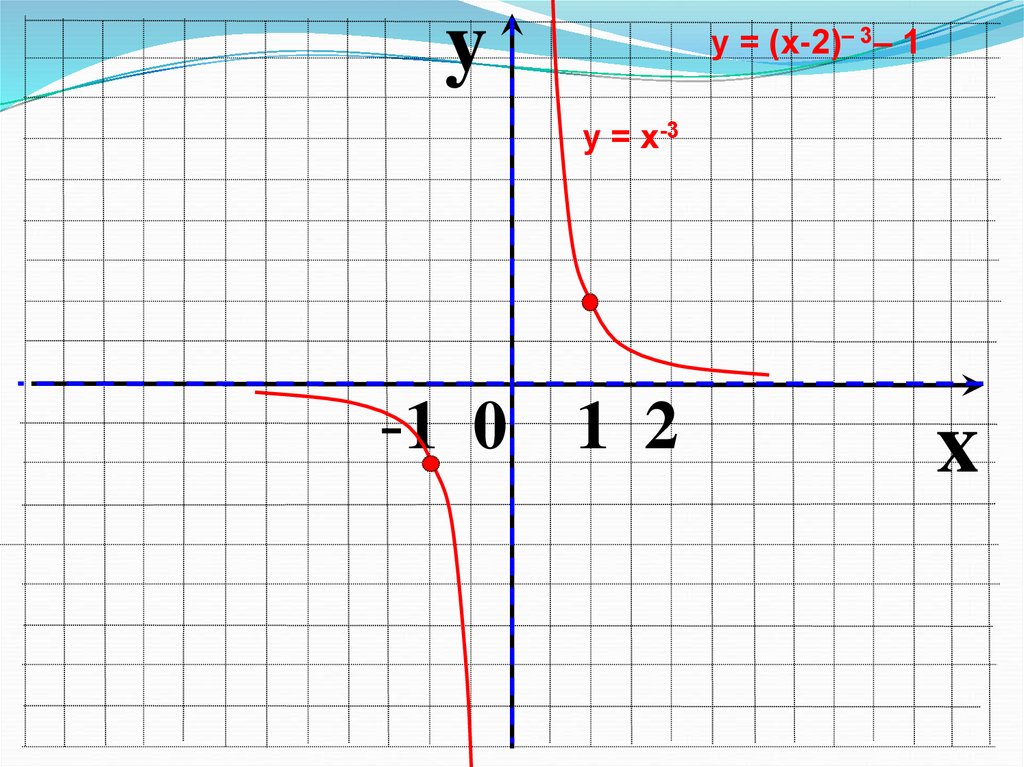
11.

y
у = (х-2)– 3– 1
у = х-3
-1 0 1 2
x

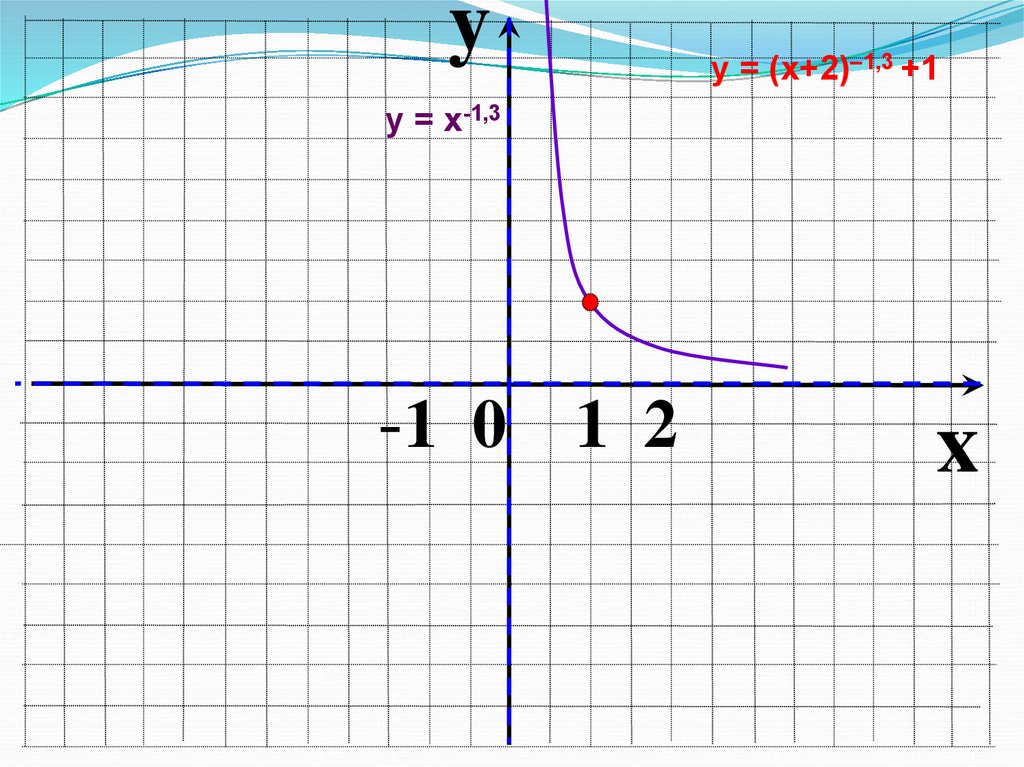
12.

y
у = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x

13.

Функция вида
y a , a 0, a 1
x
называется показательной функцией с
основанием а и показателем х

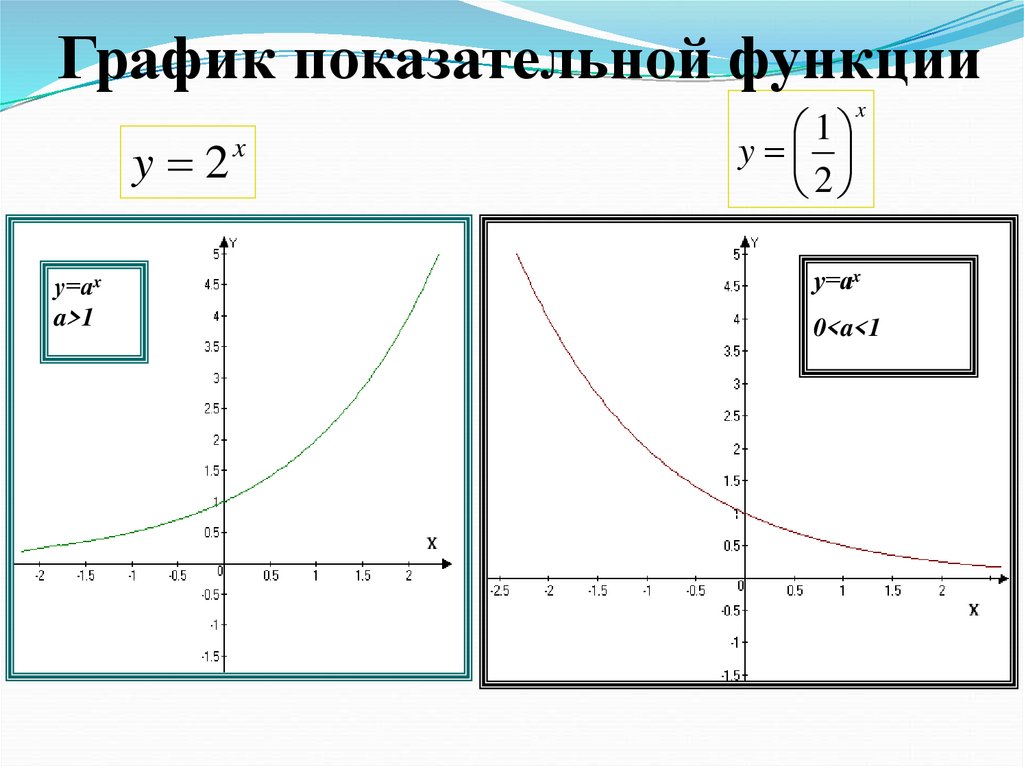
14.

График показательной функции
y 2
у=аx
a>1
x
1
y
2
x
у=аx
0<a<1

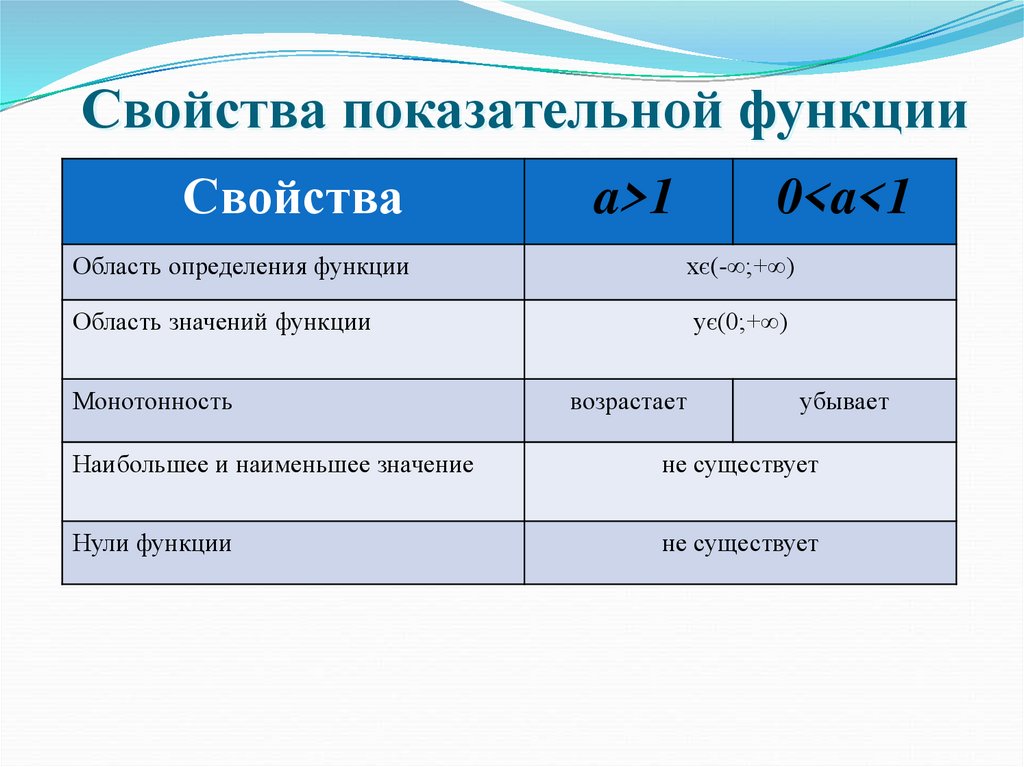
15. Свойства показательной функции

Свойства
a>1
0<a<1
Область определения функции
хє(-∞;+∞)
Область значений функции
ує(0;+∞)
Монотонность
возрастает
убывает
Наибольшее и наименьшее значение
не существует
Нули функции
не существует

16.

Какие из данных функций являются
показательными?
1. y 2 x;
4. y 7 x .
2. y x ;
5. y
2
3. y 2 ;
6. y
2
x
x
x

17.

Укажите возрастающую функцию:
1
1. y
4
x
1
2. y
7
1
3. y
2
x
x
4. y 10
x

18.

Укажите убывающую функцию:
x
1. y 5 ;
x
1
3. y ;
2
x
2. y 10 1;
x
1
4. y 1.
2

19.

Вычислите значение функции y x
точках:
1
4; ; 0; 0,01
9
1)
2 32
y 4 2
5
2 2
5
2)
3)
5
2
5
1
1 1
1
y
243
9 3
3
2
y 0 0
5
2
4)
2
1
1
1
y
5
10
100 10
5
2
в

20.

Дана функция y a x b . Вывести
правило, по которому можно, не
выполняя построение графика данной
функции, найти область значений
функции
Если
y a b, то E y b;
Если
y a b, то E y b;
x
x

21.

у=0,3х-4
Решение:
0,3х>0, для всех х
0,3х -4>0-4
у>-4
Ответ: (-4;+∞)

22.

Найдите область значений функций:
a) y 3 x 1 ;
x
7
б ) y 6;
9
в) y 17 x 2;
x
2
г ) y 8;
5
0;
6;
2;
8;

23.

Установите соответствие между графиками,
изображёнными на рисунке и степенными функциями:
1) y sin 2 x cos 2 x 2;
2) y sin arcsin x;
1
3) y
;
1 x
4) y 2log2 x ;
x3
5) y 2 ;
x