Исследование функций и построение графиков. Теоремы Ферма, Ролля, Лагранжа

1. Исследование функций и построение графиков

2. Исследование функций

Теорема Ферма.
Теорема Ролля.
Теорема Лагранжа.

3. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
Теорема Ролля.
Теорема Лагранжа.

4. Исследование функций

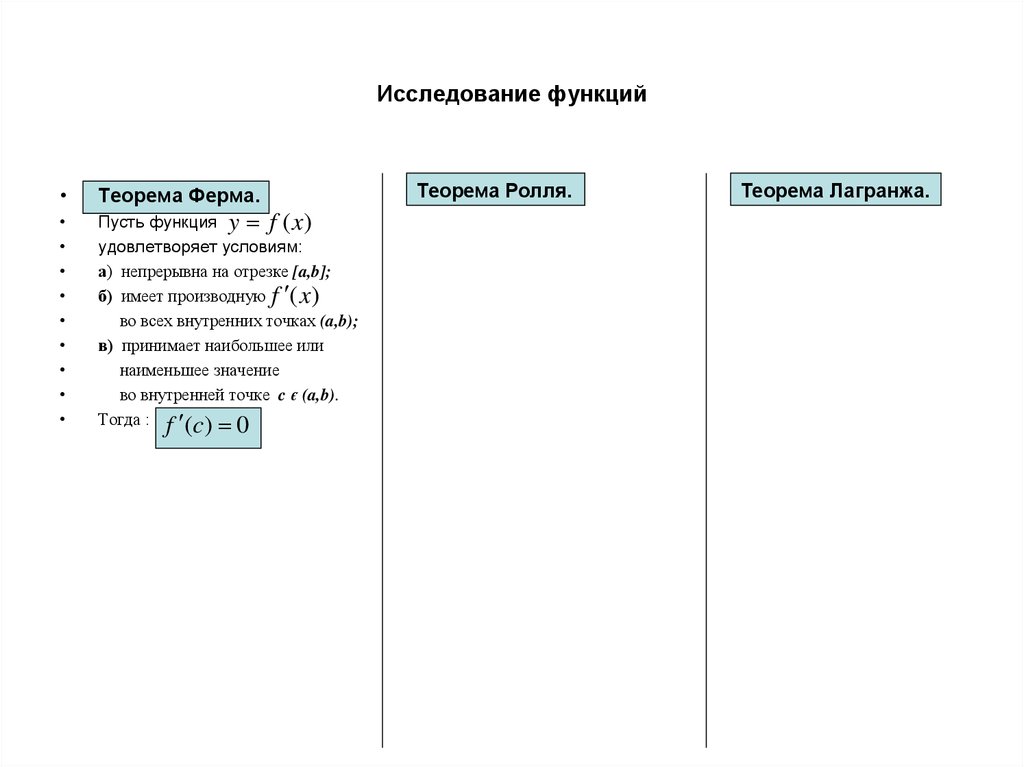
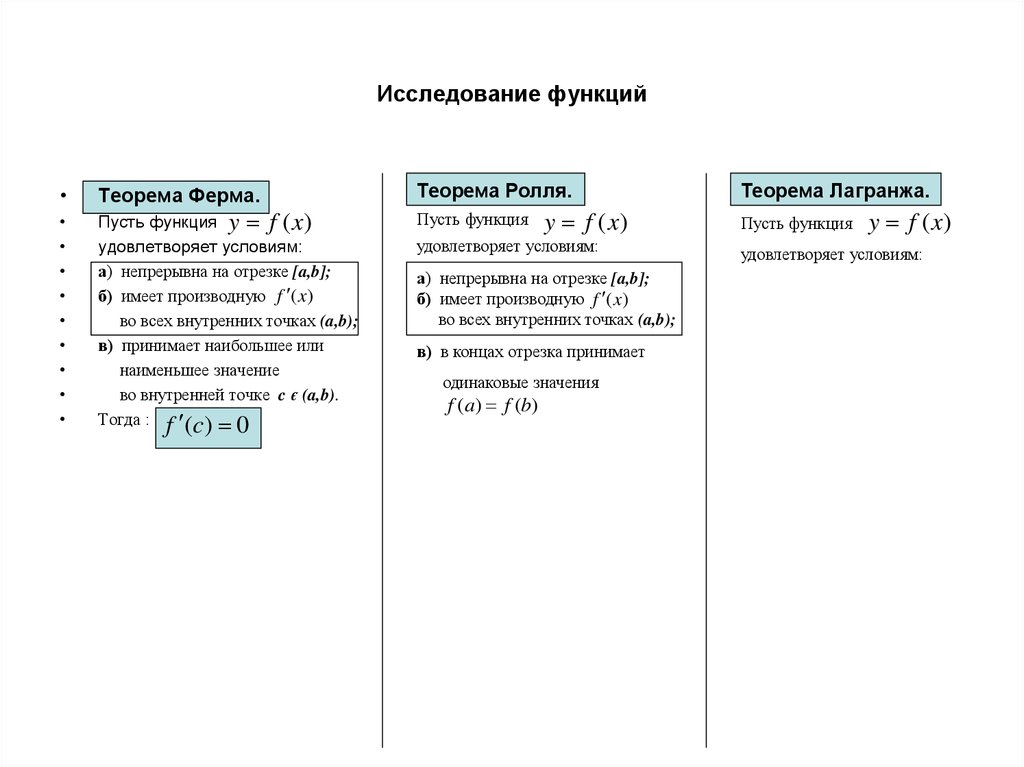
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Теорема Лагранжа.

5. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

6. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

7. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

8. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:

9. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);

10. Исследование функций

Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Теорема Ролля.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
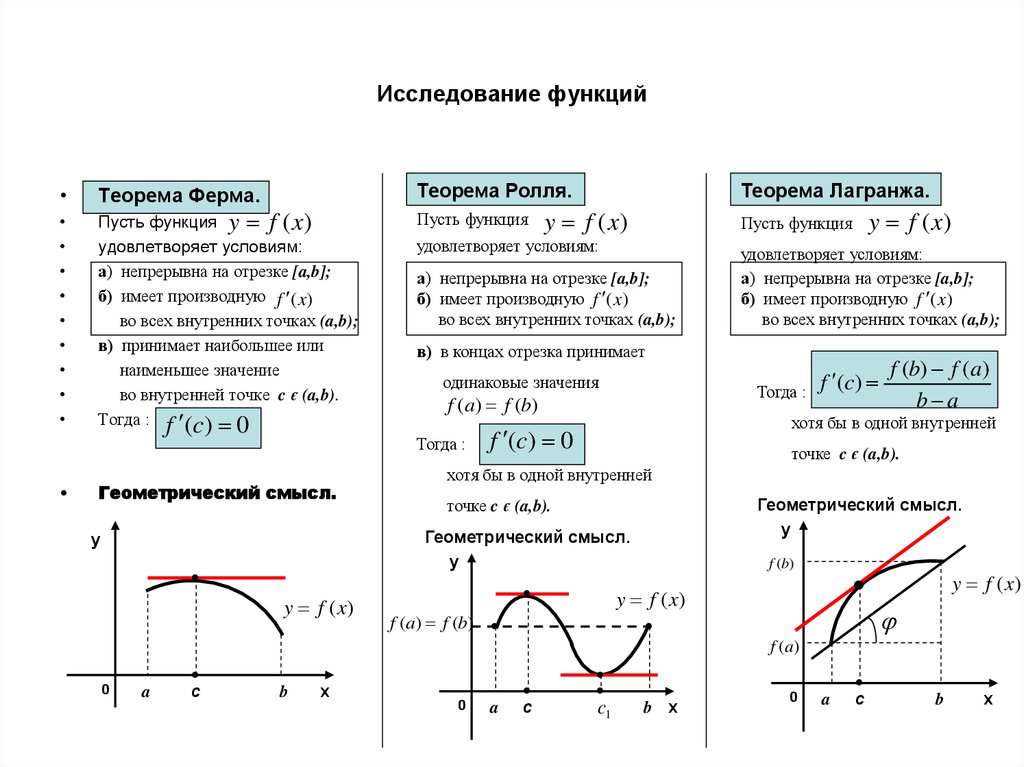
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
точке c є (a,b).

11. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Геометрический смысл.
y
0
a
c
b
x
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
Теорема Лагранжа.
Пусть функция
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
f (a) f (b)
Тогда :
f (c) 0
хотя бы в одной внутренней
точке c є (a,b).
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
точке c є (a,b).

12. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Геометрический смысл.
y f (x)
a
c
y f (x)
Пусть функция
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
b
x
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
f (a) f (b)
Тогда :
точке c є (a,b).
y f (x)
f (a) f (b)
0
a
f (b) f (a)
b a
точке c є (a,b).
хотя бы в одной внутренней
c
f (c)
хотя бы в одной внутренней
f (c) 0
Геометрический смысл.
y
y
0
Пусть функция
Теорема Лагранжа.
c1
b x

13. Исследование функций

Теорема Ролля.
Теорема Ферма.
Пусть функция y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) принимает наибольшее или
наименьшее значение
во внутренней точке c є (a,b).
Тогда : f (c) 0
Геометрический смысл.
Пусть функция
Теорема Лагранжа.
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
y f (x)
удовлетворяет условиям:
а) непрерывна на отрезке [a,b];
б) имеет производную f (x)
во всех внутренних точках (a,b);
в) в концах отрезка принимает
одинаковые значения
Тогда :
f (a) f (b)
Тогда :
f (c)
f (b) f (a)
b a
хотя бы в одной внутренней
f (c) 0
точке c є (a,b).
хотя бы в одной внутренней
Геометрический смысл.
y
точке c є (a,b).
Геометрический смысл.
y
y
y f (x)
Пусть функция
f (b)
y f (x)
f (a) f (b)
y f (x)
f (a)
0
a
c
b
x
0
a
c
c1
b x
0
a
c
b
x

14. Исследование функций

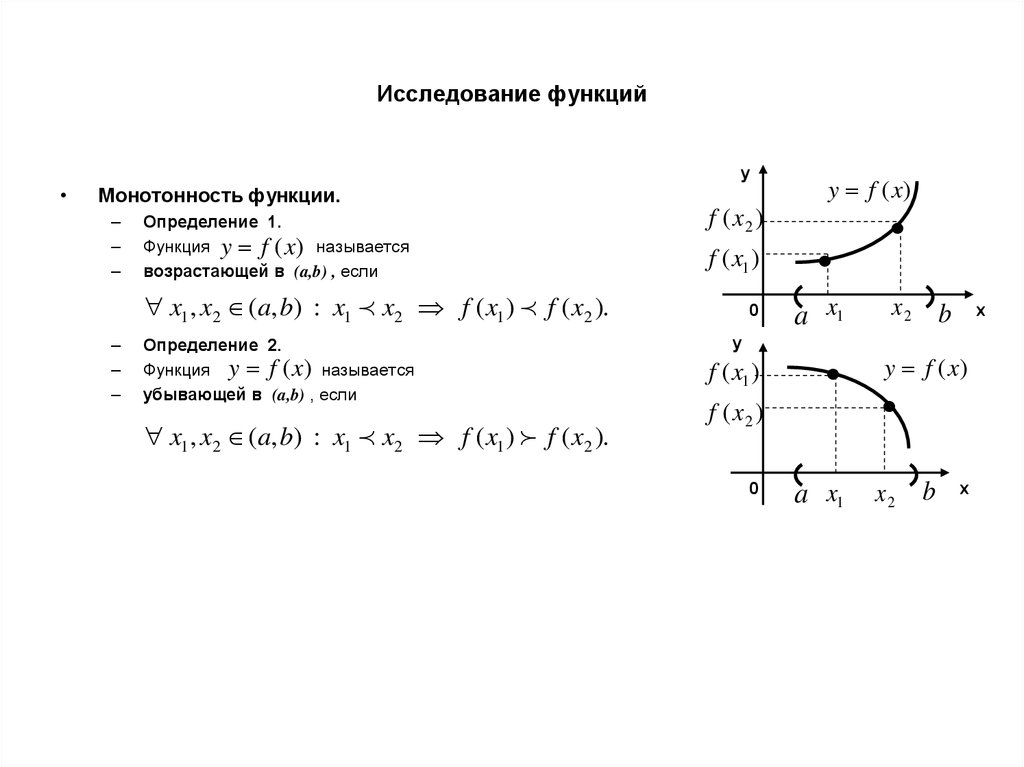
y
Монотонность функции.
–
–
–
Определение 1.
Функция y f (x) называется
возрастающей в (a,b) , если
f ( x2 )
f ( x1 )
x1 , x2 (a, b) : x1 x2 f ( x1 ) f ( x2 ).
–
–
–
Определение 2.
Функция y f (x) называется
убывающей в (a,b) , если
x1 , x2 (a, b) : x1 x2 f ( x1 ) f ( x2 ).
y f (x)
0
a x1
f ( x1 )
y
f ( x2 )
0
a x1
x2
b
x
y f (x)
x2
b
x

15. Исследование функций

Теорема.
Пусть
Тогда:
f ( x) x (a, b) .
1) f ( x) 0 f ( x) возраст аетв (a, b) ;
2) f ( x) 0 f ( x) убывает в (a, b) .
Доказательство.
1.
2.
x1 , x2 (a, b) : x1 x2
f ( x2 ) f ( x1 ) f (c)( x2 x1 ) ; c ( x1 , x2 ) (a, b).
f ( x) 0 x (a, b) f (c) 0
f ( x2 ) f ( x1 ) 0 f ( x2 ) f ( x1 ) ( убывает) .
3.
f ( x) 0 x (a, b) f (c) 0
f ( x2 ) f ( x1 ) 0 f ( x2 ) f ( x1 ) (возрастает) .

16. Исследование функций

y
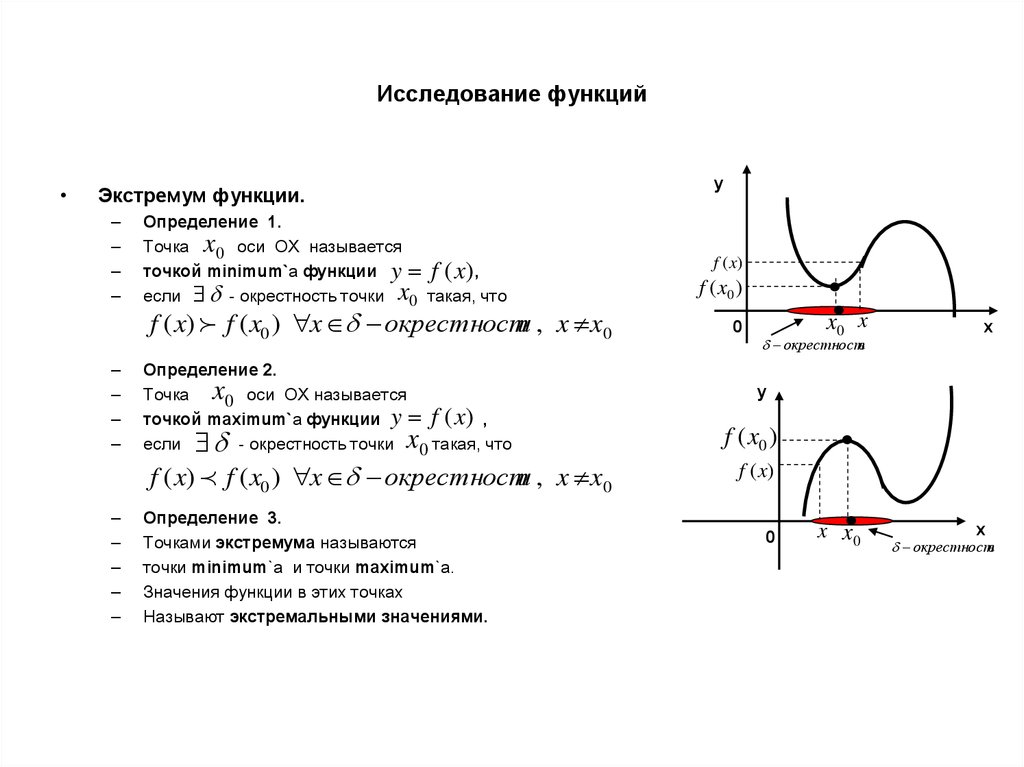
Экстремум функции.
–
–
–
–
–
–
–
–
Определение 1.
Точка x0 оси ОХ называется
точкой minimum`а функции y f (x),
если - окрестность точки x0 такая, что
f ( x) f ( x0 ) x окрестности , x x0
Определение 2.
Точка
0 оси ОХ называется
точкой maximum`а функции y f (x) ,
если
- окрестность точки 0 такая, что
x
x
f ( x) f ( x0 ) x окрестности , x x0
–
–
–
–
–
Определение 3.
Точками экстремума называются
точки minimum`а и точки maximum`а.
Значения функции в этих точках
Называют экстремальными значениями.
f (x)
x 0 x
f ( x0 )
0
окрестность
x
y
f ( x0 )
f (x)
0
x x 0
x
окрестность

17. Исследование функций

Необходимый признак экстремума.
–
–
Теорема.
1. y f ( x )
определена
в окрест ности т очки x0
–
( включая т очку x0 )
.
2. точка x0 точка экстремума
–
Доказательство.
–
Пусть
–
Определение 3.
–
Критическими точками называются
–
точки оси ОХ , в которых
–
либо
f ( x0 )
f ( x ) 0
f ( x0 ) 0 либо
f ( x0 ) не существует
y f (x) - удовлетворяет теореме Ферма
f ( x) 0
не существует.
f ( x0 ) 0

18. Исследование функций

Достаточные признаки экстремума.
–
–
Определение.
Пусть y f (x) определена и непрерывна
–
–
в δ - окрестности точки x0 (включая точку x0 ).
Пусть f (x) в δ - окрестности точки x0
–
(за исключением, быть может, точки
–
Говорят, что
–
меняет знак с « + » на « - », если
–
Говорят, что
–
меняет знак с « - » на « + » , если
x0 ).
f (x) при переходе через точку x0
при x x0 : f ( x) 0 , при x x0 : f ( x) 0 .
f (x)
при переходе через точку
x0
при x x0 : f ( x) 0 , при x x0 : f ( x) 0 .

19. Исследование функций

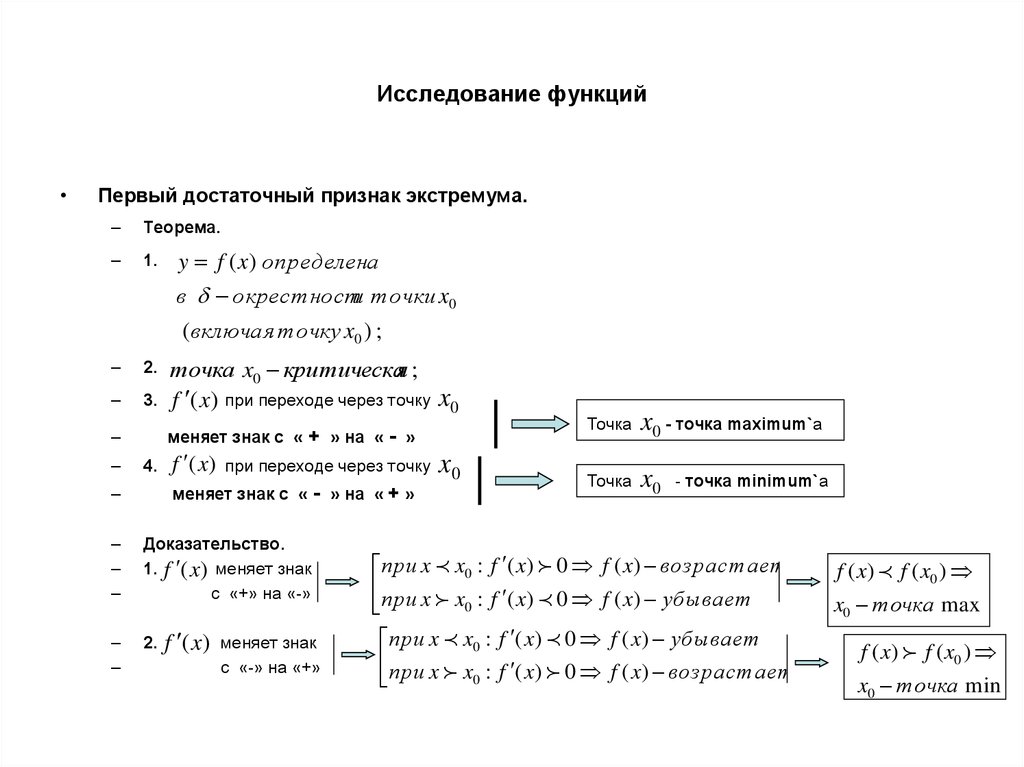
Первый достаточный признак экстремума.
–
Теорема.
–
1.
y f ( x) определена
в окрест ности т очки x0
(включая т очку x0 ) ;
–
2.
–
3.
–
–
точка x0 критическая ;
f (x) при переходе через точку x0
меняет знак с « + » на « - »
4.
–
f (x)
при переходе через точку
меняет знак с « - » на « + »
–
–
–
Доказательство.
1. f (x) меняет знак
с «+» на «-»
–
–
2.
f (x)
меняет знак
с «-» на «+»
x0
Точка
x0 - точка maximum`а
Точка
x0
- точка minimum`а
при x x0 : f ( x) 0 f ( x) возраст ает
при x x0 : f ( x) 0 f ( x) убывает
при x x0 : f ( x) 0 f ( x) убывает
при x x0 : f ( x) 0 f ( x) возраст ает
f ( x) f ( x0 )
x0 точка max
f ( x) f ( x0 )
x0 точка min

20. Исследование функций

Второй достаточный признак экстремума.
–
Теорема.
–
1.
y f ( x) определена
в окрест ности т очки x0
(включая т очку x0 ) ;
–
2.
f ( x0 ) 0 ;
–
3.
f ( x0 ) 0
Точка
–
4.
f ( x0 ) 0
Точка
x0
- точка minimum`а
x0 - точка maximum`а

21. Исследование функций

–
–
–
–
–
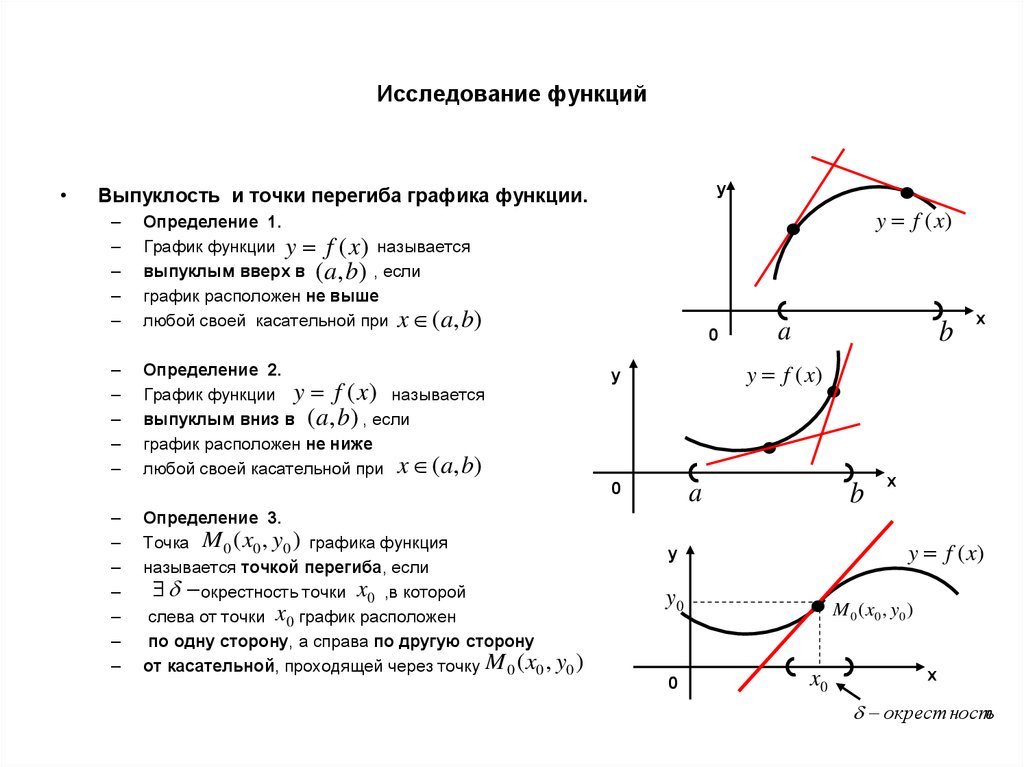
Определение 1.
График функции y f (x) называется
выпуклым вверх в ( a, b) , если
график расположен не выше
любой своей касательной при x (a, b)
–
–
–
–
–
Определение 2.
График функции y f (x) называется
выпуклым вниз в ( a, b) , если
график расположен не ниже
любой своей касательной при x (a, b)
Определение 3.
Точка M 0 ( x0 , y0 ) графика функция
называется точкой перегиба, если
окрестность точки x0 ,в которой
слева от точки x0 график расположен
по одну сторону, а справа по другую сторону
от касательной, проходящей через точку M 0 ( x0 , y0 )
y f (x)
b
a
0
y f (x)
y
x
0
–
–
–
–
–
–
–
y
Выпуклость и точки перегиба графика функции.
x
b
a
y f (x)
y
y0
M (x , y )
0
x0
0
0
0
x
окрестность

22. Исследование функций

Достаточный признак выпуклости.
–
Теорема.
–
1.
–
2.
f ( x) x (a, b) ;
f ( x) 0
x ( a, b)
–
3.
f ( x) 0
x ( a, b)
График функции
выпуклый вниз
y f (x)
в ( a, b)
y f (x)
выпуклый вверх в ( a, b)
График функции

23. Исследование функций

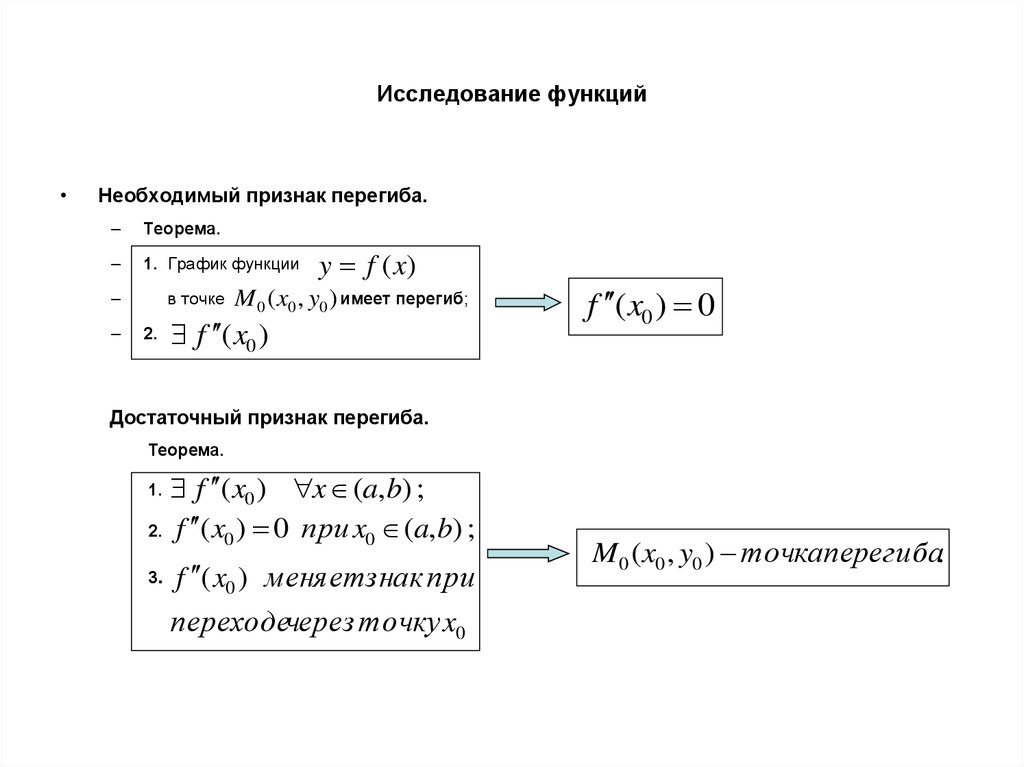
Необходимый признак перегиба.
–
Теорема.
–
1. График функции
–
–
в точке
2.
y f (x)
M 0 ( x0 , y0 ) имеет перегиб;
f ( x0 )
f ( x0 ) 0
Достаточный признак перегиба.
Теорема.
f ( x0 ) x (a, b) ;
2. f ( x0 ) 0 при x0 (a, b) ;
1.
3.
f ( x0 ) меняетзнак при
переходечерез точку x0
M 0 ( x0 , y0 ) точка перегиба.

24. Исследование функций

y
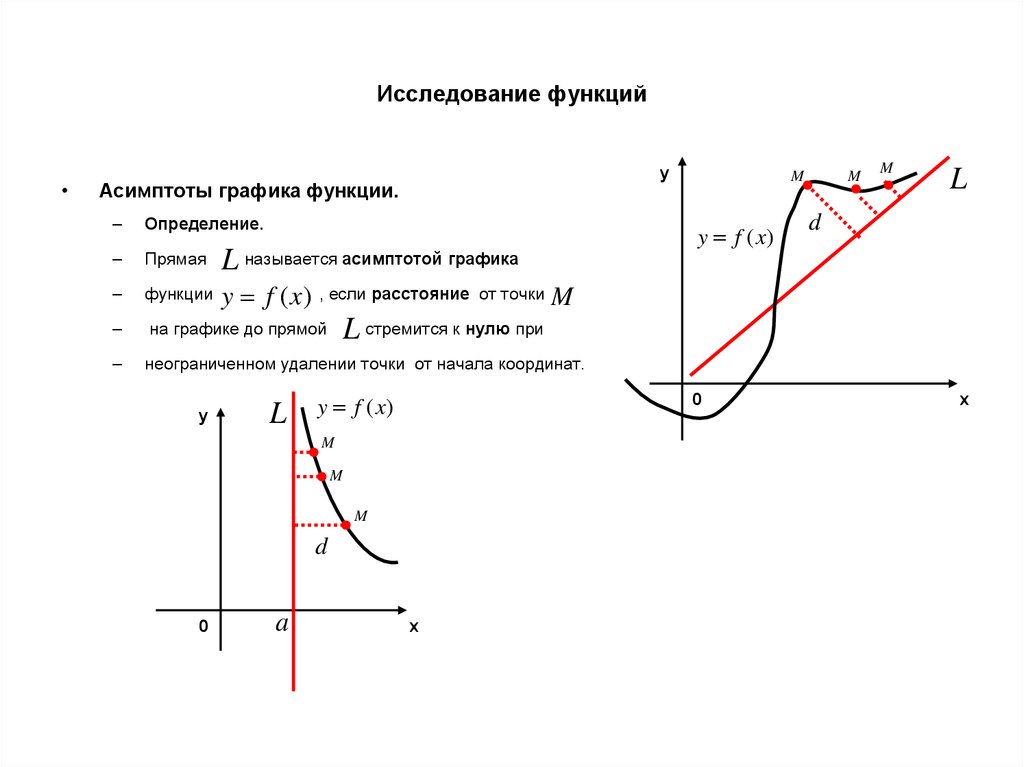
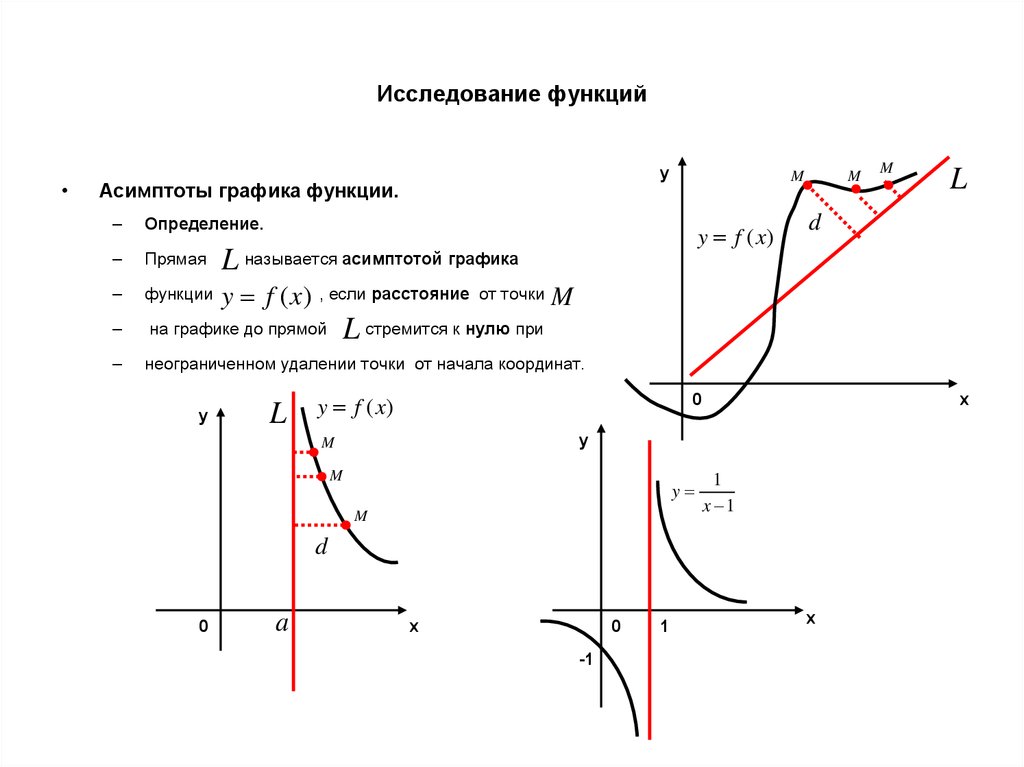
Асимптоты графика функции.
–
Определение.
–
Прямая
L называется асимптотой графика
–
функции
y f (x) , если расстояние
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
от точки
M
y f (x)
M
M
L
d
M
L стремится к нулю при
0
x

25. Исследование функций

y
Асимптоты графика функции.
–
Определение.
–
Прямая
L называется асимптотой графика
–
функции
y f (x) , если расстояние
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
y
L
y f (x)
M
L
d
M
0
M
M
d
a
y f (x)
M
L стремится к нулю при
M
0
от точки
M
x
x

26. Исследование функций

y
Асимптоты графика функции.
–
Определение.
–
Прямая
L называется асимптотой графика
–
функции
y f (x) , если расстояние
–
на графике до прямой
–
неограниченном удалении точки от начала координат.
y
L
от точки
M
y f (x)
M
d
M
y f (x)
0
x
y
M
y
M
1
x 1
d
a
L
L стремится к нулю при
M
0
M
x
0
-1
1
x

27. Исследование функций

Теорема 1.
–
–
x a
Прямая
является вертикальной асимптотой,
если хотя бы один из пределов
lim f ( x) или lim f ( x)
x a 0
–
равен
x a 0
или
Теорема 2.
y kx b является
f ( x)
lim
k
x
x
Прямая
если
и
наклонной асимптотой,
lim f ( x) kx b
x
Замечание. Горизонтальная асимптота - частный случай
наклонной асимптоты при k 0

28. Исследование функций

Общая схема исследования функции.
–
–
–
–
–
–
–
Первый этап.
1. Область определения, точки разрыва.
2. Четность, нечетность.
3. Периодичность.
4. Точки пересечения с осями координат.
5. Асимптоты графика.
6. Поведение при x
Уточненное исследование с помощью
первой производной.
1. Точки экстремума (вычислить экстремальные значения).
2. Интервалы монотонности.
Исследование с помощью второй производной.
1. Точки перегиба (вычислить значение функции и угловой коэффициент).
2. Интервалы выпуклости.

29. Исследование функций

Пример 1.
y x 8x 16 x
3
–
Исследовать функцию и построить график
–
1. О.О.Ф.
–
2. Четность, нечетность:
2
x R
y( x) ( x) 8( x) 16( x) x 8x 16 x ( x 8x 16 x)
y ( x) y ( x) ; y ( x) y ( x) Функция общего вида
3
2
3
–
3. Непериодическая.
–
4. Точки пересечения с осями координат:
с Оу:
С Ох:
2
3
2
x 0 y 0 M 0 (0,0)
y 0 x 8 x 16 x 0
3
2
x( x 8 x 16) 0
2
x( x 4) 0
2
x0 0, x1 4
M 0 (0,0), M 1 (4,0)

30. Исследование функций

–
5. Асимптоты.
а) вертикальных асимптот нет;
б) наклонные:
y kx b
f ( x)
x 8x 16 x
2
k lim
lim
lim ( x 8 x 16)
x
x
x
x
x
3
2
Наклонных асимптот нет
–
x
3
2
lim ( x 8 x 16 x)
6. Поведение при
x
lim ( x 8 x 16 x)
3
x
2

31. Исследование функций

Исследование с помощью первой производной.
2
y 3x 16 x 16
16 16 4 3 16 16 8
6
6
2
y 0 3x 16 x 16 0 x1, 2
4
x1 4, x2
3
2
y
+
max
4
3
4
4 3
4 2
4 256
y ( ) ( ) 8 ( ) 16
9,5
3
3
3
3 27
y (4) 0
-
min
4
+
х

32. Исследование функций

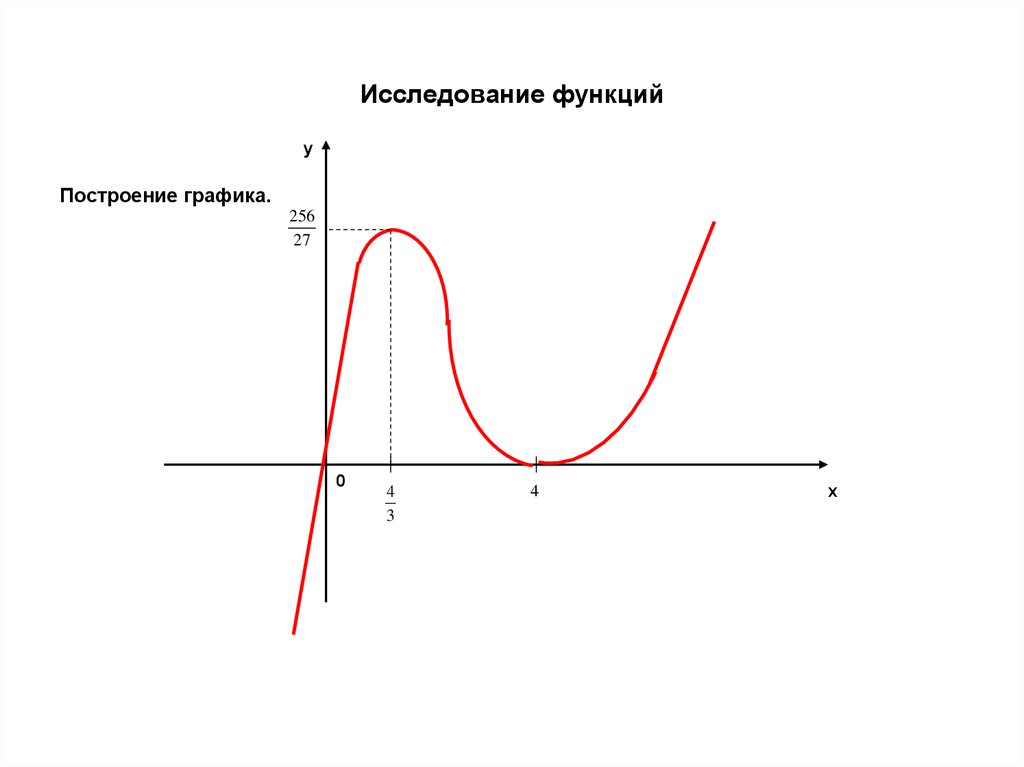
y
Построение графика.
256
27
0
4
3
4
x

33. Исследование функций

Исследование с помощью второй производной.
y (3x 16 x 16) 6 x 16
2
y 0 6 x 16 0 x
y
+
16 8
6 3
8
3
х

34. Исследование функций

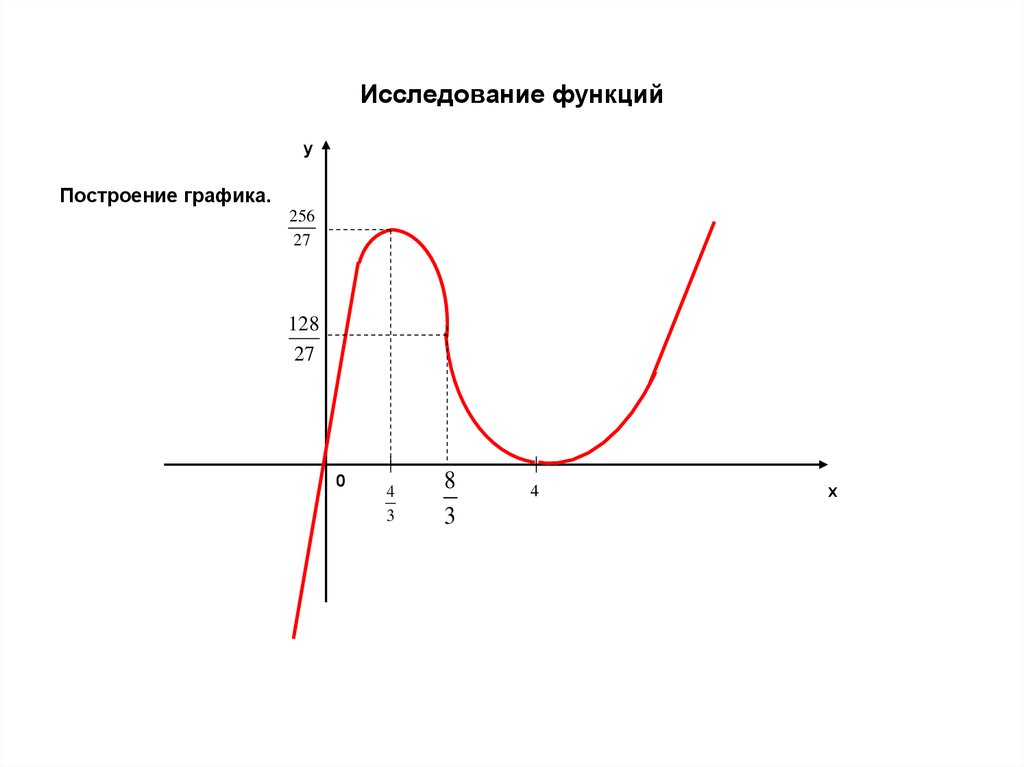
y
Построение графика.
256
27
128
27
0
4
3
8
3
4
x

35. Исследование функций

Пример 2.
–
–
Исследовать функцию и построить график
.
2
x
1. О.О.Ф.: x 1 ; lim
1 x
x2
lim
x 1 o 1 x
x 1 o
–
–
–
–
x2
y
1 x
x 1 т очка разрыва
вт орогорода.
2. Четность, нечетность:
( x) 2
x2
y ( x)
1 ( x) 1 x
y( x) y( x) ; y( x) y( x)
3. Непериодическая.
4. Точки пересечения с осями координат:
5. Асимптоты:
• а) вертикальные: x 1 .
• б) наклонные: y kx b ;
Функция
общего
вида.
x 0; y 0.
f ( x)
x
lim
1 ;
x
x
x
1 x
x2
b lim f ( x) kx lim
x 1 .
x
x 1 x
k lim
y x 1

36. Исследование функций

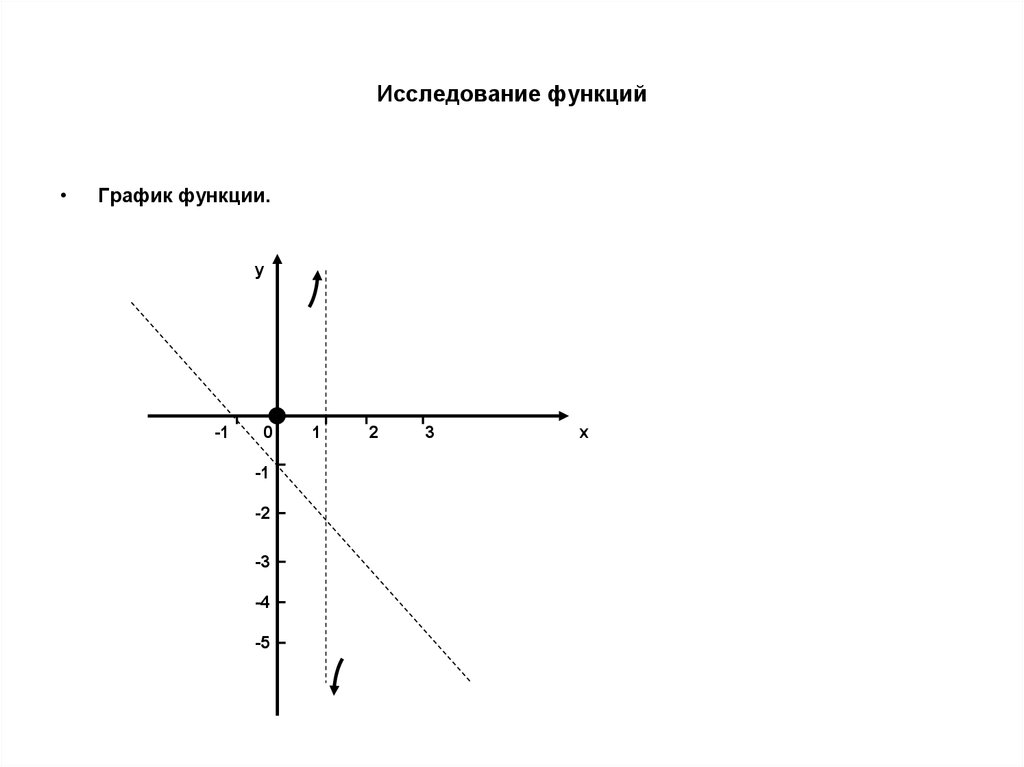
График функции.
y
-1
0
-1
-2
-3
-4
-5
1
2
3
x

37. Исследование функций

График функции.
y
-1
0
1
2
-1
-2
-3
-4
-5
?
3
x

38. Исследование функций

Исследование с помощью первой производной.
2 x(1 x) x 2 ( 1) x(2 x)
y
;
(1 x) 2
(1 x) 2
y 0 x1 0 ; x2 2 ;
y1 0 ; y2 4 ;
y не существует: x 1
y
min
0
1
max
2
x

39. Исследование функций

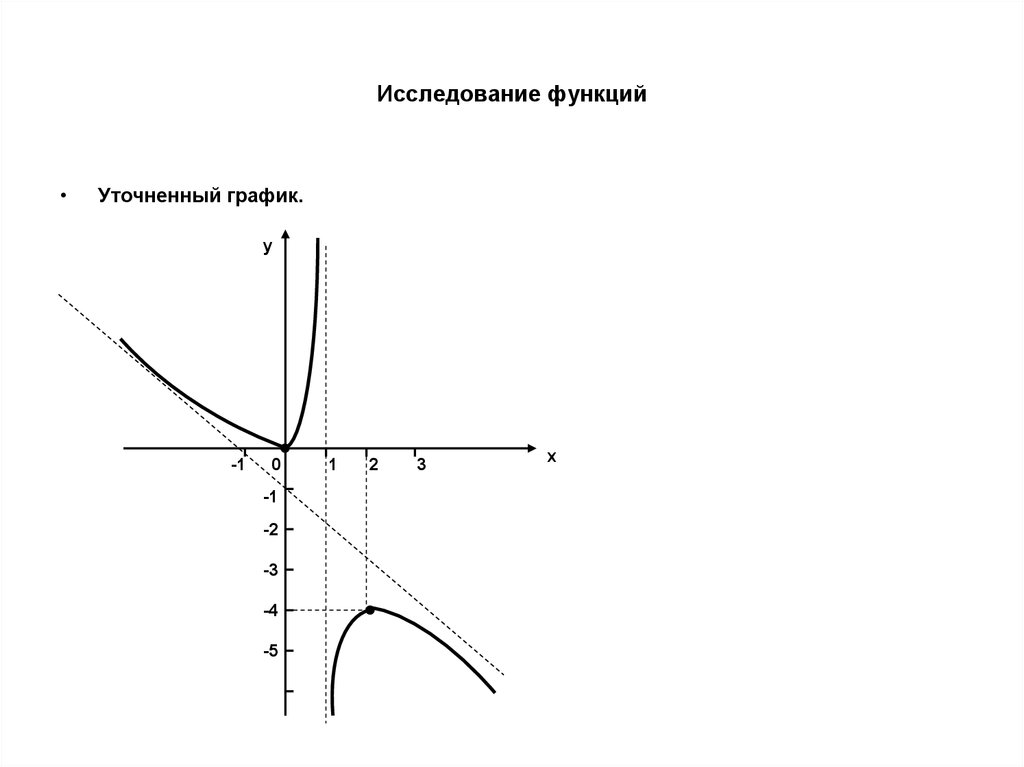
Уточненный график.
y
-1
0
-1
-2
-3
-4
-5
1
2
3
x