Темпоральная логика

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Неклассические логики»
Тема «Темпоральная логика»
Автор Анисимова Л.В.
Ижевск
2014

2.

Темпоральная логика
При всей широте использования классической логики в науке,
технике и в обычной жизни очевидны ее ограничения.
Классическая логика основывается на самой примитивной
модели истины, т. е. формулы логики могут принимать значения
только "да" и "нет", она не позволяет выразить степень
уверенности/неуверенности в истинности высказывания.
Поэтому появились логики, в которых истинностное значение
логических формул зависит от момента времени, в котором
вычисляются значения этих формул-это темпоральные логики.
Курс "Неклассические логики"
Тема "Темпоральные логики"
2

3.

История
Темпоральная логика начала
складываться в 50-е годы XX в.
прежде всего благодаря работам
англ. логика А. Н. Прайора, хотя
первые попытки учесть роль
временного фактора в логическом
выводе относятся еще к
античности (Аристотель, Диодор
Кронос).
Артур
Прайор
Курс "Неклассические логики"
Тема "Темпоральные логики"
3

4.

Суть темпоральной логики
Рассмотрение реального процесса во времени
заставляет отступиться от двузначной логики.
Например, между периодом, когда идёт дождь, и
периодом, когда дождь прекратился, имеется
промежуточное состояние, когда количество капель
слишком мало, для того что-бы сказать, что идёт
дождь, но слишком велико, чтобы утверждать, что
дождь уже закончился. Таким образом, появляется
третье значение высказывания:“ни истинно, ни ложно”.
Курс "Неклассические логики"
Тема "Темпоральные логики"
4

5.

Суть темпоральной логики
Необходимость оперировать высказываниями, истинность
которых меняется со временем, возникает часто. Например,
высказывание: "Путин - президент России" истинно только в
определенный период времени. Высказывание "Светит солнце",
ложное сегодня, может стать истинным завтра. Утверждение "Я
голоден" станет ложным после того, как я поем.
_______________________________________________________
Многие утверждения, в которых вводятся причинноследственные отношения, также связаны со временем:
"Если я видел ее раньше, то я узнаю ее при встрече";
"Раз Персил - всегда Персил";
"Мы не друзья, пока ты не извинишься".
Курс "Неклассические логики"
Тема "Темпоральные логики"
5

6.

Отличие от классической логики
Отличие темпоральной логики от классической попытаемся
объяснить на примере. свойств технических систем, обладающих
динамикой:
С1: Посланный запрос когда-нибудь в будущем будет обработан;
С2: Лифт никогда не пройдет мимо этажа, вызов от которого
поступил, но еще не обслужен.
Элементарные (атомарные) утверждения в этих высказываниях
могут быть истинны в один момент времени и ложны в другой.
Мы не можем адекватно представить утверждение С1 с
помощью такой формулы логики высказываний:
Послан(R)” Обработан(R) (то есть если запрос R послан, то он
обработан).
Курс "Неклассические логики"
Тема "Темпоральные логики"
6

7.

Отличие от классической логики
Действительно, в классической логике утверждения обычно
понимаются как истинные либо ложные независимо от времени, а
утверждение C1 явно различает разные моменты времени. Оно
утверждает, что если в некоторый момент времени t запрос R послан,
то в какой-то будущий момент времени
t ' > t он будет обработан.
Попытаемся выразить эти свойства с помощью логики предикатов
первого порядка, вводя в употребление такие выражения, как "событие
р наступило в момент t". Утверждение С1 при этом будет выглядеть
так:
Утверждение С2 в логике предикатов выглядит так (здесь ЛифтN(t)) утверждение: Лифт в момент t находится на этаже n):
Курс "Неклассические логики"
Тема "Темпоральные логики"
7

8.

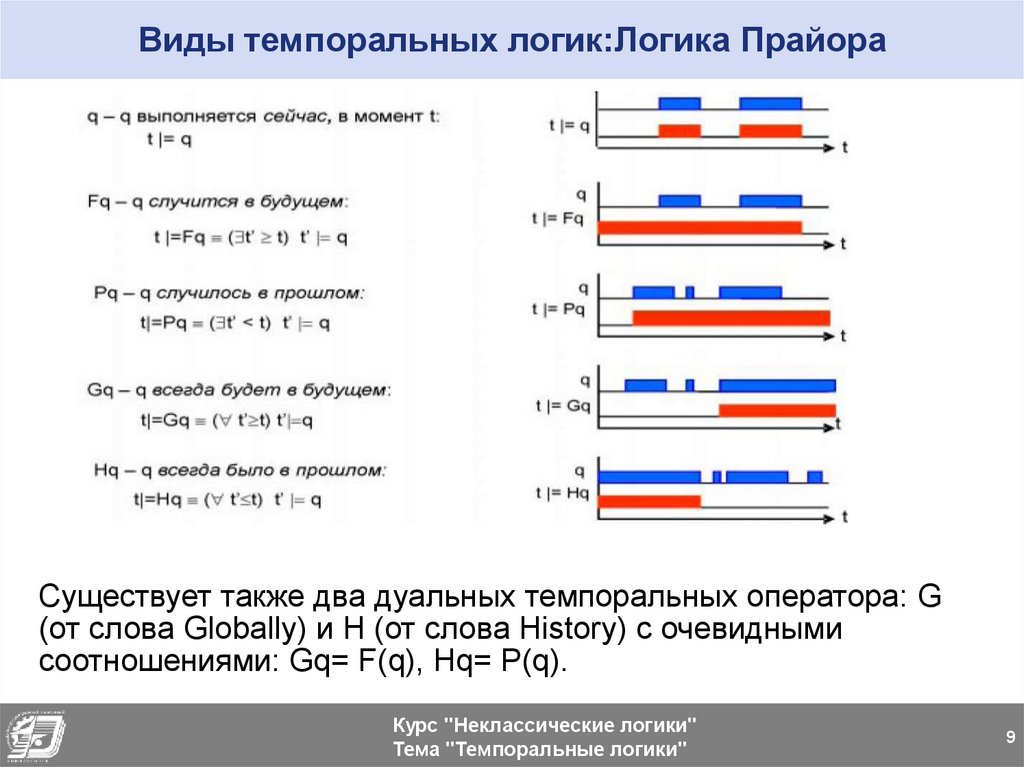
Виды темпоральных логик:Логика Прайора
В логике Прайора были впервые введены две
модальности: F (от Future): "когда-нибудь в будущем
будет истинно ..." и P (от Past): "когда-то в прошлом
было истинно ..."
Рассмотрим, как с помощью этих операторов формально
записать некоторые утверждения:
Джейн вышла замуж и родила ребенка:
Р( Джейн выходит замуж /\ Fджейн рожаеm ребенка)
Джейн родила ребенка и вышла замуж:
Р(Джейн рожает ребенка /\ Fджейн выходum замуж)
Курс "Неклассические логики"
Тема "Темпоральные логики"
8

9.

Виды темпоральных логик:Логика Прайора
Существует также два дуальных темпоральных оператора: G
(от слова Globally) и H (от слова History) с очевидными
соотношениями: Gq= F(q), Hq= P(q).
Курс "Неклассические логики"
Тема "Темпоральные логики"
9

10.

Виды темпоральных логик:Логика линейного времени (LTL)
Современная
темпоральная логика
линейного времени (LTL,
Linear Time Logic)
является наследницей
временной логики Tense
Logic Артура Прайора.
LTL разработана
израильским ученым
Амиром Пнуэли для
спецификации свойств
параллельных
технических систем. За
разработку этой логики в
1966 г. Амир Пнуэли был
награжден премией
Тьюринга.
Амир Пнуэли
Курс "Неклассические логики"
Тема "Темпоральные логики"
10

11.

Виды темпоральных логик:Логика линейного времени (LTL)
В LTL максимально упрощены все включенные в нее
концепции.
Во-первых, в LTL темпоральными операторами расширена
простейшая логика высказываний, формулы которой
строятся из конечного числа атомарных предикатов
(утверждений) и булевых операций над ними.
Во-вторых, в новую логику включено минимальное число
темпоральных операторов, которые определяют
характеристики истинности высказываний, упорядоченных во
времени. Таких операторов только два, U(Until) и X(NextTime).
Логика LTL не включает темпоральных операторов прошлого.
Основания для этого очевидны: прошлое для технических
систем менее важно, чем их будущее поведение,
начинающееся с момента их включения.
Курс "Неклассические логики"
Тема "Темпоральные логики"
11

12.

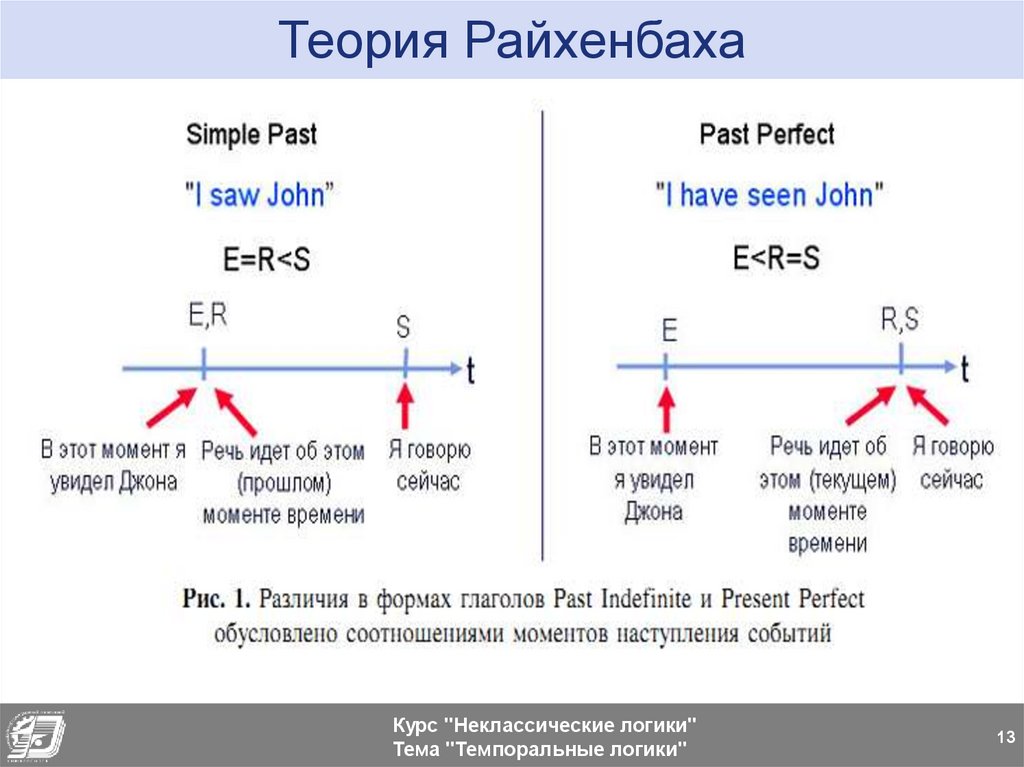
Теория Райхенбаха
Попытка построения формальной модели, учитывающей время
в высказываниях, была предпринята философом и логиком
Гансом Райхенбахом для изучения глагольных времен
английского языка. Время глагола в предложении
характеризуется соотношением моментов наступления событий.
Используя соотношения во времени двух моментов: момента S, в
который сделано высказывание (Speech time), и момента Е
наступления события, о котором говорится в высказывании
(Event time), можно образовать только три простых времени
глагола - настоящее, прошедшее и будущее с соотношениями
соответственно E=S, E<S и S<E. Для того чтобы покрыть
большое число различных глагольных времен, Рейхенбах ввел
третий момент - момент R точки референции (Reference time), то
есть момента, на который ссылается высказывание.
Курс "Неклассические логики"
Тема "Темпоральные логики"
12

13.

Теория Райхенбаха
Курс "Неклассические логики"
Тема "Темпоральные логики"
13

14.

Синтаксис темпоральной логики
Фиксируется бесконечное счётное множество Р. Элементы из Р
называются про-стыми высказываниями и обычно обозначаются через p,
q, r, или p1, p2, p3, …. (Модальные) формулы строятся из атомов и
символа 1 («истина») с помощью логических связок & и ¬, и модальности
□ («квадрат»):
1) каждый атом p ∈P является формулой;
2) символ 1 является формулой;
3) если А и В – формулы, то ¬A, A & B, [F]A и [P]A – формулы.
(Темпоральные формулыиспользуют вместо символа квадрата символы:
[F] и [P]
(будущего и прошлого). Вместо А применяется запись: [F]A или [P]A)
Дополнительные логические связки
Символ 0 (ложь) и связки ∨, →, ↔ введём как сокращенные записи
операций:
0 = ¬1, А ∨В = ¬(¬А & ¬В), А →В = ¬(А &¬В), А ↔В = (А →В) & (В
→А).
Курс "Неклассические логики"
Тема "Темпоральные логики"
14

15.

Приоритет операций
С целью уменьшения количества скобок будем
предполагать, что приоритеты
унарных связок выше, чем приоритеты бинарных и
располагаются в порядке убывания
следующим образом:
¬, , ◊, [F], [P], <F>, <P>, &, ∨, →, ↔.
Для унарных операций взаимные приоритеты не имеют
значения (и могут счи-таться равными). Например, ◊А & ¬В
→С означает: (((◊А) & ( (¬В))) →С).
Курс "Неклассические логики"
Тема "Темпоральные логики"
15

16.

Смысловые значения модальностей
Уточним, что мы понимаем под символами: □ , ◊, [F], [P], <F>, <P>.
Значения этих символов зависят от области применения и могут
обладать неодинаковыми свойствами.
Например, □А = «А обязательно», ◊А = «А возможно» обладают
свойством □А →А
(«Если сегодня в Москве обязательно идёт дождь, то в Москве
идёт дождь»). А модальности □А = «необходимо А», ◊А =
«допустимо А» не обладают этим свойством. Например,
высказывание: «Если необходим дождь, то идёт дождь» – может
быть ложным.
Другие значения модальностей: □А = «А известно» и ◊А =
«А
предположительно», □А = «А всегда верно» и ◊А = «А иногда
верно». При доказательстве правильности программ используются
модальности □А = «после окончания работы программы будет
верно А» и ◊А = «программа может закончиться так, что А станет
верным».
Курс "Неклассические логики"
Тема "Темпоральные логики"
16

17.

Примеры
Рассмотрим смысловые значения формул модальной логики:
□□А = «известно, что А известно»;
□◊А = «необходимо, чтобы А было допустимо»;
□А →А = «если известно, что А верно, то А – верно»;
[P][P]А →[P]А = «если всегда было верно, что А было верно всегда,
то А всегда
было верно»;
□□А → □А = «если известно, что А известно, то А известно»;
□А → □□А = «если агент знает А, то он знает, что он знает А»;
А →[F]<P>А = «если А верно, то в будущем всегда будет верно, что
в некоторый
момент прошлого было верно А»;
◊¬<P>А = «возможно, что А не было верным никогда»;
□А & □В → □(А & В) = «если А и В известны, то известно А & В».
Курс "Неклассические логики"
Тема "Темпоральные логики"
17

18.

English Русский Правила