fedyaev

1. Федяев Константин Сергеевич Институт космических исследований РАН

Методы решения
почти вырожденных
и плохо обусловленных
задач линейного программирования

2.

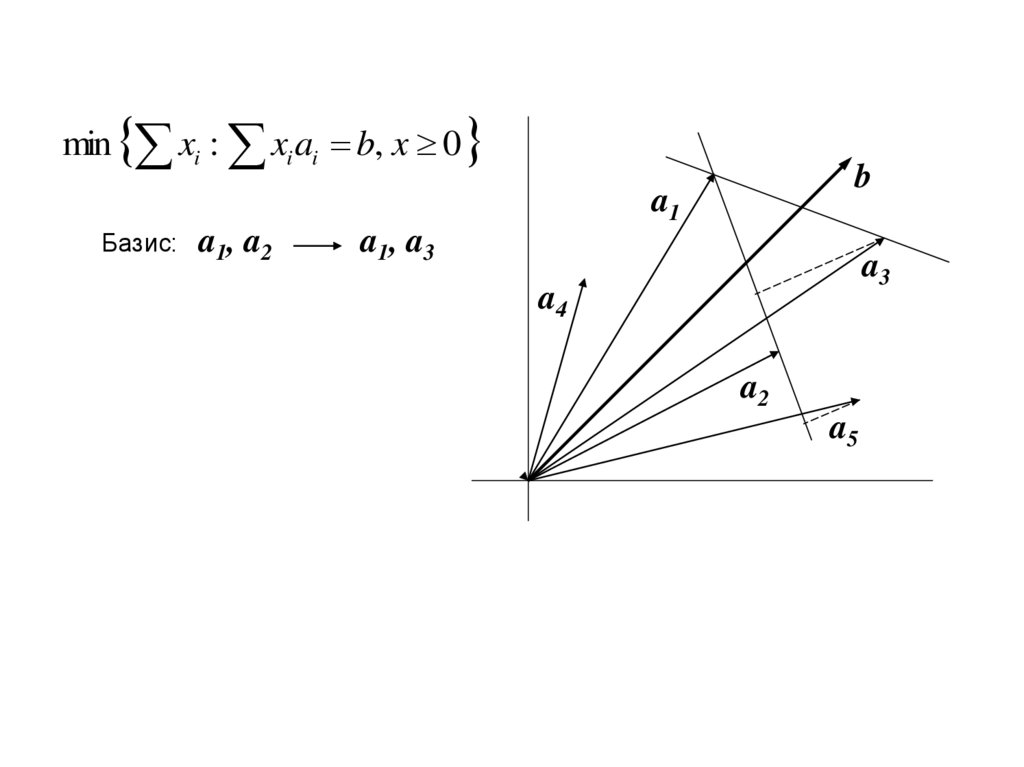
min xi : xi ai b, x 0
b
a1
Базис:
a1, a2
a1, a3
a3
a4
a2
a5

3. Задача линейного программирования Симплекс-метод

min ci xi : xi ai b, xi 0, 1 i n , ai , b R m
1. B ai - текущий базис,
xB B 1b,
2. : ' B cB'
3. j a j c j ' a j ,
s min j
4. s 0 оптимум.
Иначе :
xi
5. B as ,
min : i 0
r
i
6. ar as ~
z z s
1
xr

4. Вырожденность

B (m m) - текущий базис, x1 0,..., xk 0, xk 1 0,..., k m
r k
xr
r
0, ~
z z - вырожденная итерация
Вспомогательная задача (Бахшиян, 1989):
Обозначим V (ak 1 ,..., am ), L (V ) R m k , R m L(V )
hi Sai , S - матрица перехода от R m к L(V )
D min i yi : hi yi d , yi 0, 1 i n k , hi , d R m k
y
*
D* текущий базис B оптимален
D* строится новый базис основной задачи

5. Построение нового базиса в основной задаче

m k
hs ˆ i hi , ˆ i 0 i,
*
D
i 1
ˆ ˆ ' Bˆ 0
s
s
ˆ i , 1 i m k ,
i 1,
i s,
0
иначе
i gi , gi : ai gi hi , hi L(V )
xi
min : i 0
r 1 i k i
xr
(ak 1 ,..., am , ar ) (прообразы векторов h1 ,..., hm k , hs )
~
xi xi i ,
~
z z s

6.

n
n
min xi : xi ai b, xi 0, ai a( ) (cos , sin )
i 1
i 1
1
1 0, 2 2 , 3 4 ,..., n n ,
b
0
Обычный алгоритм:
(a1 , a2 ) : x1 1, x2 0
(a1 , a3 ) : x1 1, x3 0
(a1 , a4 ) : x1 1, x4 0
a2
...
(a , a ) : x 1, x 0
1
n
1
a3
n
Алгоритм Бахшияна:
V (a2 ),
hi - проекции ai на OY
h2 h3 ... hn 0
h3
a4
an
a1 b
3 4 ... n 0
d
min i yi : hi yi d k
базис (a1 , a2 ) оптимален
y
hk

7.

n
n
min xi : xi ai b, xi 0, ai a( ) (cos , sin )
i 1
i 1
1 3
1 2
, 4
,...,
0.001 1 , 2 2 , 3
2
2
1 n 2
a2
n 1
, n
2
a3
(a , a ) : x 1, x 0
1
2
1
2
(a1 , a3 )
...
(a1 , an ) : x1 x2 1
a4
2
xi
a0 1a1 2 a2 , i
x1 x2
(a0 , a2 ) - вырожденный базис
min i yi : hi yi d
y
an
a0
b
a1
(a0 , a2 ) (a1 , an )

8. Почти вырожденные задачи

n
n
min ci xi : xi ai b, xi 0, 1 i n
i 1
i 1
ОЗ
1
x
B
b, x1 0,..., xk 0, xk 1 ,..., xm малы
B (m m) - базис, B
I 0 i0 k 1,..., m , i0 k
xi
a0 i ai , i
,
i I 0
xj
c0 i ci .
j I 0
y ( y0 , y1 ,..., yn ) : y0 xi ,
i I 0
i I 0
0, i I 0
yi
xi иначе
n
n
min c0 y0 ci yi : y0 a0 yi ai b, yi 0, 0 i n
i 1
i 1
РЗ

9.

n
n
min ci xi : xi ai b, xi 0, 1 i n
i 1
i 1
n
n
min ci yi : yi ai b, yi 0, 0 i n
i 0
i 0
0, i I 0 ,
y : y0 xi , yi
i I 0
xi иначе.
ОЗ
РЗ
yi y0 i , i I 0 ,
xˆ : xˆi
i I0.
yi ,
Лемма 1. Вектор y является вырожденным допустимым базисным
решением расширенной задачи (РЗ), имеющим порядок вырожденности не меньший чем |I0|. Вектору y в задаче (РЗ) соответствует то же
значение целевой функции, что и вектору x в основной задаче (ОЗ).
Лемма 2. Вектор x̂ является допустимым решением основной задачи
(ОЗ), причем ему соответствует то же значение целевой функции, что и
вектору y в расширенной задаче (РЗ).
Лемма 3. Если вектор y является оптимальным решением расширенной
задачи (РЗ), то вектор x̂ является оптимальным решением основной
задачи (ОЗ).

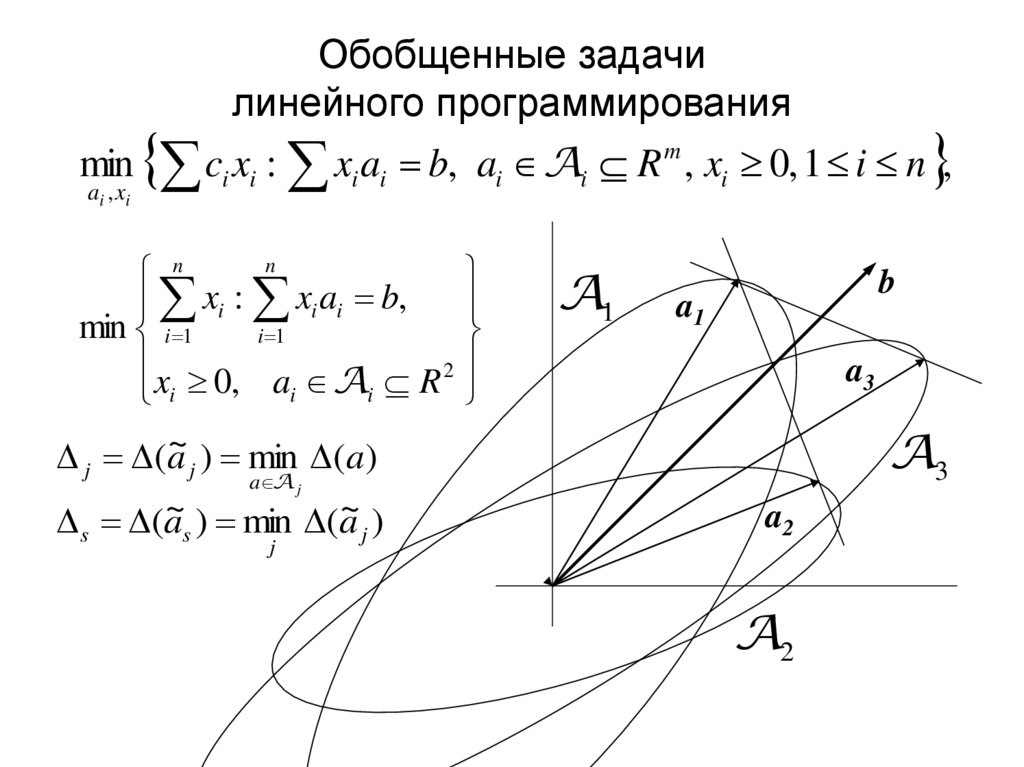
10. Обобщенные задачи линейного программирования

min ci xi : xi ai b, ai Ai R m , xi 0, 1 i n ,
ai , xi
n
n
xi : xi ai b,
min i 1
i 1
x 0, a A R 2
i
i
i
j (a~ j ) min (a)
a A j
(a~ ) min (a~ )
s
s
j
j
A1
b
a1
a3
A3
a2
A2

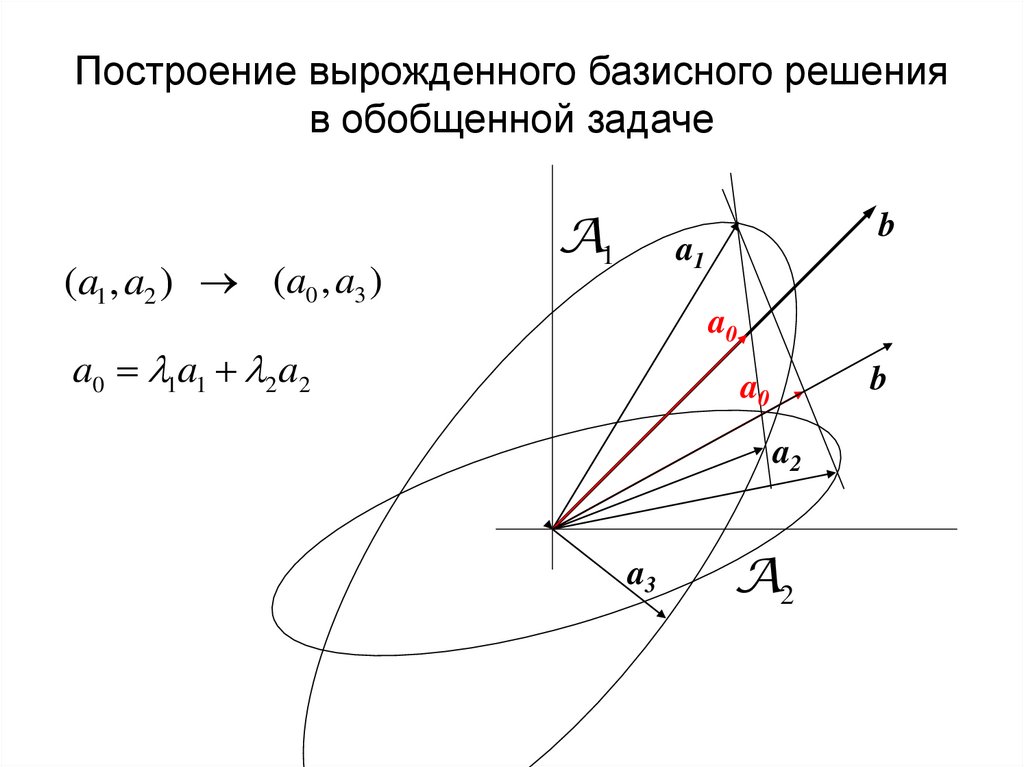
11. Вырожденные обобщенные задачи

min ci xi : xi ai b, ai Ai R m , xi 0, 1 i n ,
ai , xi
B (m m) - текущий базис, x1 0,..., xk 0, xk 1 0,..., k m
V (ak 1 ,..., am ), L (V ) R m k ,
hi Sai ,
.
S : R m L (V )
hi H i h R m k : h Sa, a Ai
D min (hi ) yi : yi hi d , hi H i , yi 0, 1 i n ,
*
hi , yi
D* текущий базис B оптимален
D* строится новый базис основной задачи

12. Построение вырожденного базисного решения в обобщенной задаче

(a1 , a2 ) (a0 , a3 )
A1
b
a1
a0
a0 1a1 2 a2
b
a0
a2
a3
A2

13. Задача коррекции траектории

l R m - вектор параметров системы
ui ui (ti ) - импульс в момент времени ti
l (ti ) Pi ui - изменение вектора l в момент времени ti
b - требуемое изменение вектора l :
Pu b
i i
i
pi (ui ) - затраты на коррекцию в момент времени ti
ui xi i ,
W min pi (ui ) : Pi (ui ) b
ui
i
i
xi pi (ui ), i : pi ( ) 1
min xi : xi ai b, xi 0, ai Ai
xi , ai
i
i
Ai a : a Pi i , pi ( i ) 1

14. Задача одноимпульсной коррекции

min xi : xi ai b, xi 0, ai A
xi , ai
i
i
P diag Pii ,
Pii i, i 1,..., m
Число итераций
m
Обычный
метод
Новый метод
2
8
5+1
3
21
14+2
4
42
25+3
5
41
32+1
6
81
51+8
7
123
74+10
8
161
84+51
9
216
71+42

15. Задача L-оптимального оценивания

R m - вектор неизвестных параметров,
при i 1,..., n проводится ri измерений функции H i ' :
n
1
M i 0, D i .
ri N ,
yi H i ' i ,
ri
i 1
l j b j ' - контролируемые параметры, j 1,..., s,
lˆj ij yi - оценки параметров l j ,
i
H b
i
ij
j
i
n
n
ˆ
ui : Pi ui b
Критерий: L min N Dl j min
ui
ri
i 1
i 1
j 1
s
(Бахшиян, Соловьев, 1998)
b1
b ,
b
s
Hi
0
Pi
0
0
Hi
0
0
0
Hi

16. Задача L-оптимального оценивания

ms
ms
min xi : ai xi b, xi 0, ai Ai ,
i 1
i 1
Ai a R ms : a Pi , R s , 1
Результаты для случая полиномиальной регрессии:
1
ti
Hi
m 1
t
i
2 m 8
s 2
Число итераций
m
Обычный
метод
Новый метод
2
26
12
3
46
19
4
62
25
5
79
25
6
98
28
7
146
37
8
129
44