ФОЭ_ Тема 3_2021.09.12

1.

ФИЗИЧЕСКИЕ ОСНОВЫ
ЭЛЕКТРОНИКИ
Тема 3
ПРОВОДИМОСТЬ
ПОЛУПРОВОДНИКОВ И МЕТАЛЛОВ

2.

Электрический ток в материалах
• Электрический ток может протекать только в том случае, когда в
материале имеются свободные носители заряда (как положительного,
так и отрицательного знака), “оторванные” от конкретных атомов.
• В металлах свободные носители – электроны.
• В полупроводниках свободные носители – электроны и дырки.
• Неподвижные ионы акцепторов и доноров в электропроводности не
участвуют.
• Для оценки параметров электропроводности материалов необходимо
провести анализ:
• причину образования (накопления) в материале свободных носителей
заряда;
• зависимость концентрации n(T), р(Т) свободных носителей заряда от
различных факторов (температуры, излучения и т.п.);
• Влияние различных факторов на перемещение свободных носителей
заряда внутри кристалла (температура, магнитное и электрическое
поле, и т.п.;
• Влияние различных факторов на электрическое сопротивление
полупроводникового материала

3.

Общие характеристики
электропроводности

4.

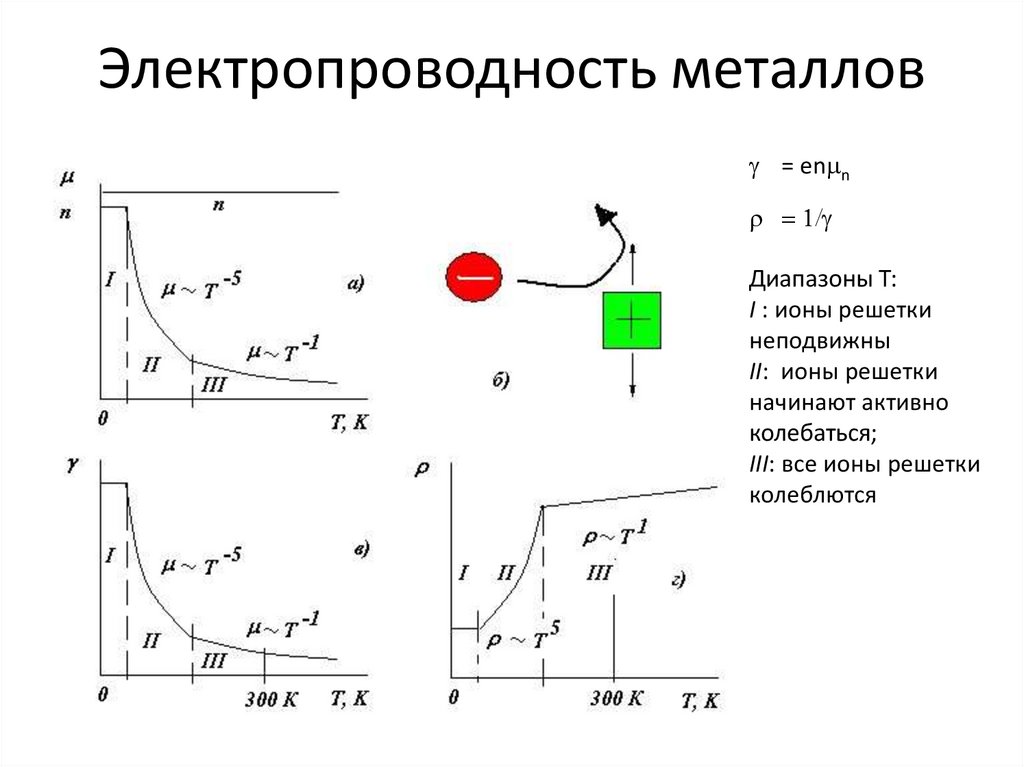
Электропроводность металлов
= enmn
= 1/
Диапазоны Т:
I : ионы решетки
неподвижны
II: ионы решетки
начинают активно
колебаться;
III: все ионы решетки
колеблются

5.

Электропроводность собственных
полупроводников
(T)= n+ p= enimn + epimp
mn≈const1; mp≈const2
(-DEз/2kT)
ni(T) = pi(T) = (NcNv)1/2e
= Aexp(-DEз/2kT)
(T) = B exp(-DEз/2kT)
ln (T) = lnB - DEз/2kT
(T)= 1/ (T)
ln (T) = lnB + DEз/2kT
Наклон: (ln 2-ln 1)/(1/T2 -1/T1) = DEз/2k
Вывод: при увеличении температуры
Проводимость собственных полупроводников
возрастает по экспоненте
Сопротивление собственных полупроводников
уменьшается по экспоненте

6.

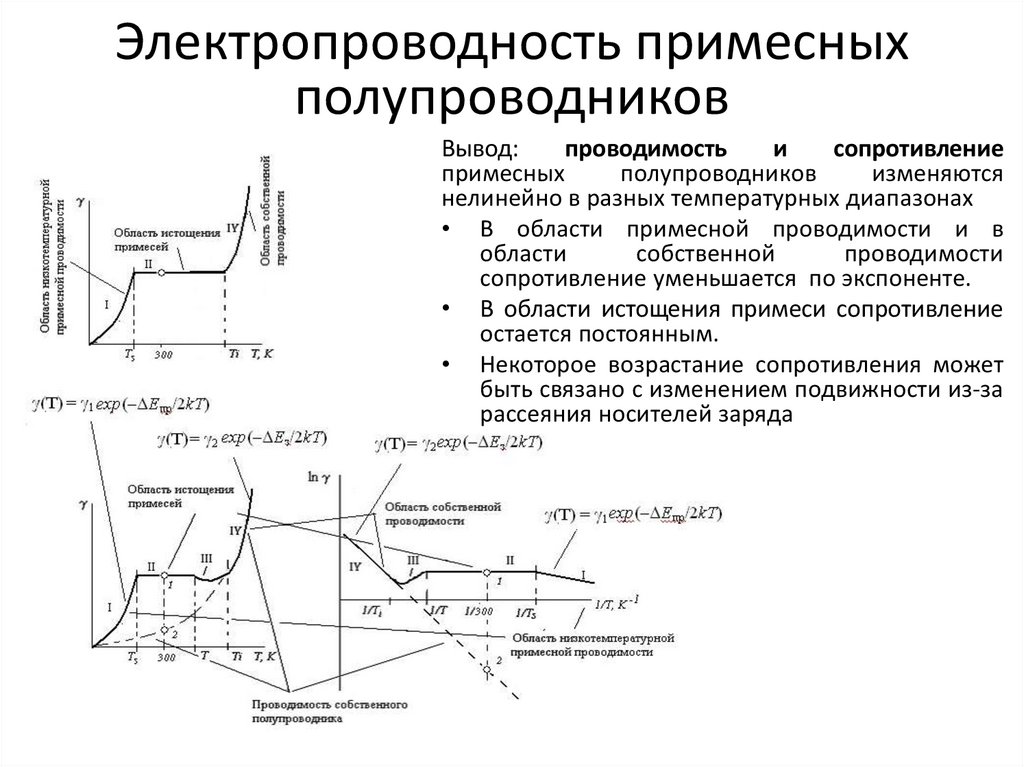
Электропроводность примесных
полупроводников
Вывод:
проводимость
и
сопротивление
примесных
полупроводников
изменяются
нелинейно в разных температурных диапазонах
• В области примесной проводимости и в
области
собственной
проводимости
сопротивление уменьшается по экспоненте.
• В области истощения примеси сопротивление
остается постоянным.
• Некоторое возрастание сопротивления может
быть связано с изменением подвижности из-за
рассеяния носителей заряда

7.

Расчет электропроводности в
полупроводниках
Задача. Т1 = 30 С. Через образец Ge p-типа проходит ток I = 100
mА. Размеры: Сечение S=0,1 мм, длина L=10 мм, напряжение
U=0,2 В; подвижность электронов и дырок: mn=0,19 м2/В·с и mp=
0,36 м2/В·с. Удельное сопротивление собственного германия i =
0,36 Ом·м. Концентрация дырок pp = 8,6·1020 1/м-3.
Решение.
1) Напряженность электрического поля: Е=U/L;
2) Сопротивление образца: R = U/I = l/S; = RS/L;
4) Удельная проводимость: а) = 1/ ; б) плотность тока j = I/S = E ; =I/SE;
5) i= enimn + epimp; = enpmn + eppmp
6) Концентрация np: np=( p-eppmp)/(emn);
7) отношение проводимостей p/ n = eppmp/enpmn;
8) Дрейфовые скорости vn=mnЕ; vp=mpЕ;
9) Время пролета длины L: tn=L/vn; tp= L/vp;
10) Концентрация собственных носителей: ni=pi=(nppp)1/2;
11) Во сколько раз изменится сопротивление собственного образца германия при
увеличении на DT=10С?
(DЕз= 0,7 эВ; k= 1,38·10˗23 Дж/К =1,38·10˗23/1,6·10-19 эВ/К = 8,625·10˗5 эВ/К;
2(Т2)/ 1(Т1) = Вexp(-DEз/2kT2)/Вexp(-DEз/2kT1)= exp[(DEз/2k)(1/T1 -1/T2)

8.

Расчет электропроводности в
полупроводниках
Задача. Т = 30 С. Через образец Ge p-типа проходит ток I = 100 mА.
Размеры: Сечение S=0,1 мм, длина L=10 мм, напряжение U=0,2 В;
подвижность электронов и дырок: mn=0,19 м2/В·с и mp= 0,36 м2/В·с.
Удельное сопротивление собственного германия i = 0,36 Ом·м.
Концентрация дырок pp = 8,6·1020 1/м-3.
Решение.
1) Напряженность электрического поля: Е=U/L; Е=0,2/10-2=20 В/м
2) Сопротивление образца: R = U/I; R = 0,2/100·10-3= 2 Ом; R= l/S
3) Удельное электрической сопротивление: = RS/L; = 2·10-4/10·10-3 =0,02 Омм;
4) Удельная проводимость: а) = 1/ ; = 1/0,02 = 50 Ом-1м-1;
б) плотность тока j = I/S = E ; =I/SE= 0,1/(10-4·20) = 50 Ом-1м-1;
5) i= enimn + epimp; = enpmn + eppmp
6) Концентрация np: np=( p-eppmp)/(emn);
np=(50 -1,6·10-19·8,6·1020·0,36)/(1,6·10-19·0,19) = 1,52·10+19 м-3
7) отношение проводимостей p/ n = eppmp/enpmn ; p/ n = 107 раз.
8) Дрейфовые скорости vn=mnЕ; vp=mpЕ; vn= 0,19·20 = 3,8 м/с; vp= 0,36·20 = 7,2 м/с;
9) Время пролета длины L: tn=L/vn; tp= L/vp; tn= 10-2/3,8 = 2,6 мc; tp= 1,38 мс
10) Концентрация собственных носителей: ni=pi=(nppp)1/2; ni=pi =
= ( 8,6·1020·1,52·10+19)1/2= (13·10+38)1/2= 3,6·1019 м-3
11) Во сколько раз изменится сопротивление собственного образца германия при увеличении на DT=10С?
(DЕз= 0,7 эВ; k= 1,38·10˗23 Дж/К =1,38·10˗23/1,6·10-19 эВ/К = 8,625·10˗5 эВ/К;
2(Т2)/ 1(Т1) = Вexp(-DEз/2kT2)/Вexp(-DEз/2kT1)= exp[(DEз/2k) ·(1/T1 -1/T2):
2(Т2)/ 1(Т1) =exp[(0,7 ·(1/303- 1/313)/(2·8,625·10˗5) =exp (0,427)= 1,53 раза

9.

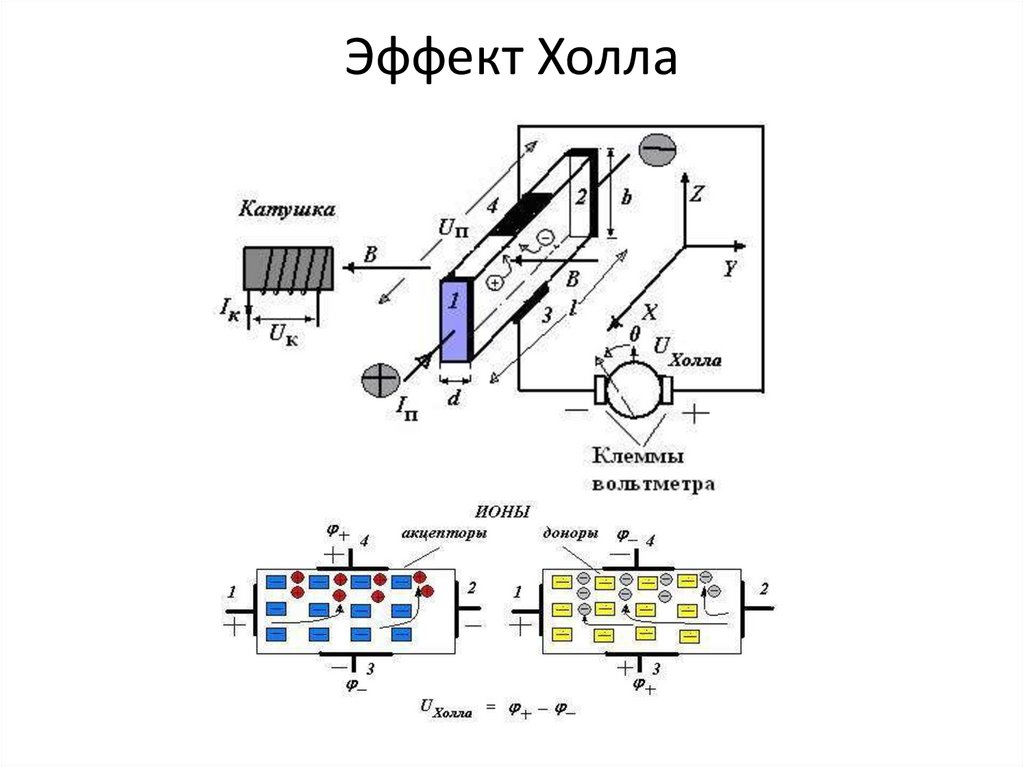
Эффект Холла

10.

Эффект Холла

11.

Эффект Холла
• Задача 1.
При исследовании эффекта Холла получены следующие значения:
толщина образца d= 0.2 мм, Ux = 5 мВ; В = 3.2 мТл; Iп = 50 мА. Определить
постоянную Холла R. (R = 6,25·10-3 м3/Кл)
• Задача 2.
При исследовании эффекта Холла получены следующие значения:
толщина образца d= 0.2 мм, Ux = 5 мВ; R = 3,12·10 3 м3/Кл; Iп = 50 мА.
Определить индукцию поля В. (В = 6.4 мТл)
• Задача 3.
Прямоугольный образец полупроводника n-типа с размерами l(длина) x d
(ширина) x b(высота) = 50 x 5 x 1 мм3 помещен в магнитное поле с
индукцией В = 0,5 Тл. Под действием U= 0,42 В по образцу протекает ток
20 мА, Ux = 6,25 мВ. Найти удельную проводимость, подвижность и
концентрацию носителей заряда, считая что один тип носителей (n = 2·1021
м 3; 476 Ом-1·м-1; 1,5 м2/В·с).
• Задача 4.
Пленка антимонида индия n-типа размерами l(длина)x b(высота)= 20x10
мм2 расположена в плоскости, перпендикулярной магнитному поля
Земли. Вычислить, какую разность потенциалов нужно приложить вдоль
пленки (по длине l ) , чтобы на других ее сторонах получить ЭДС Холла Ux =
1 мВ. Индукцию магнитного поля Земли принять равной 44 мк Тл, а
подвижность электронов 7.8 м2/(В·с). (5.82 В)