10Г през на 6.12 Параллельные прямые, перпендикулярные к плоскости

1.

Урок
геометрии в 10 классе

2.

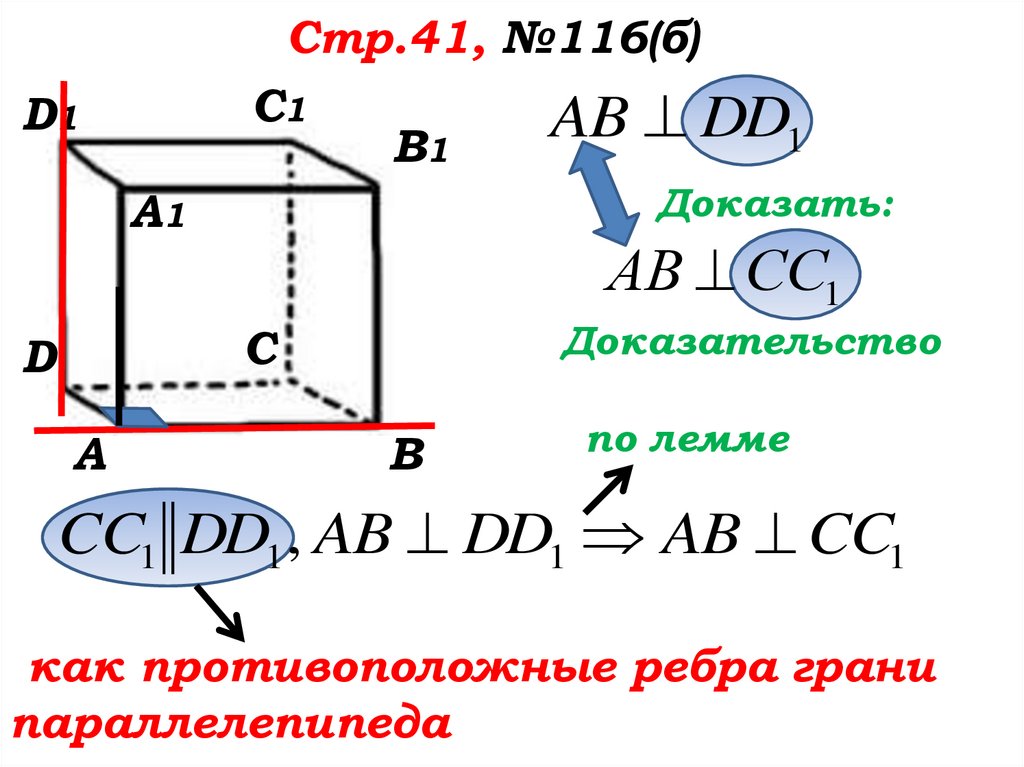
Стр.41, №116(б)
C1
D1
B1
Доказать:
А1
АВ СC1
Доказательство
С
D
А
AB DD1
В
по лемме
CC1 DD1 , AB DD1 AB CC1
как противоположные ребра грани
параллелепипеда

3.

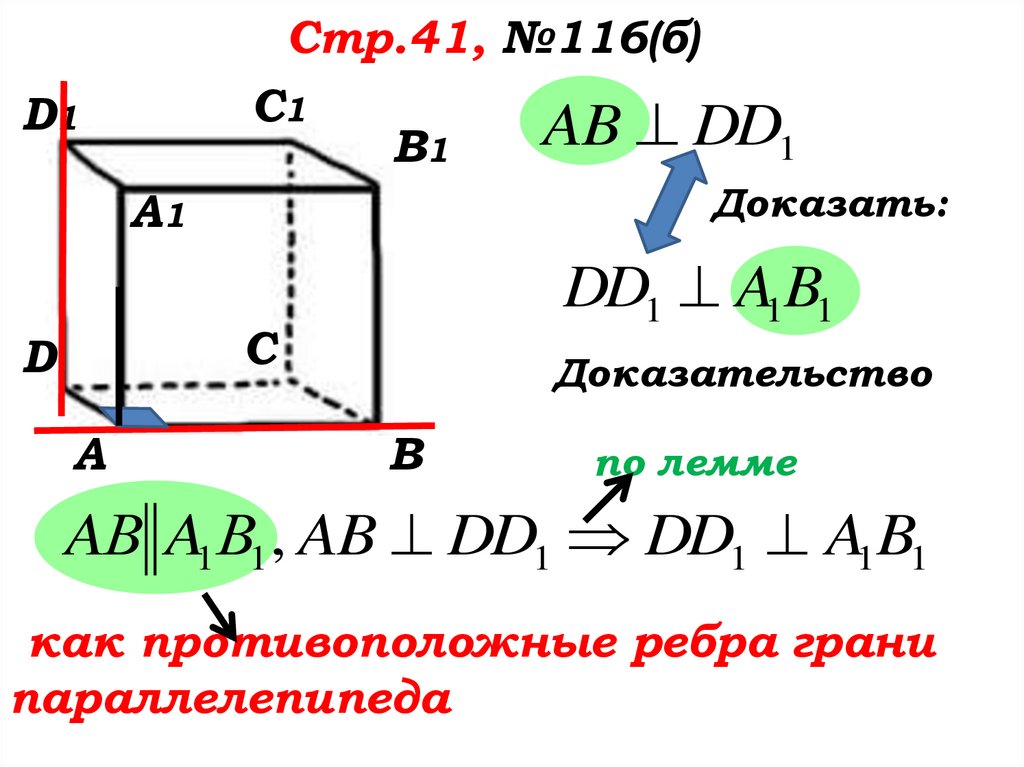
Стр.41, №116(б)
C1
D1
B1
Доказать:
А1
DD1 A1B1
С
D
А
AB DD1
Доказательство
В
по лемме
AВ A1В1 , AB DD1 DD1 A1B1
как противоположные ребра грани
параллелепипеда

4.

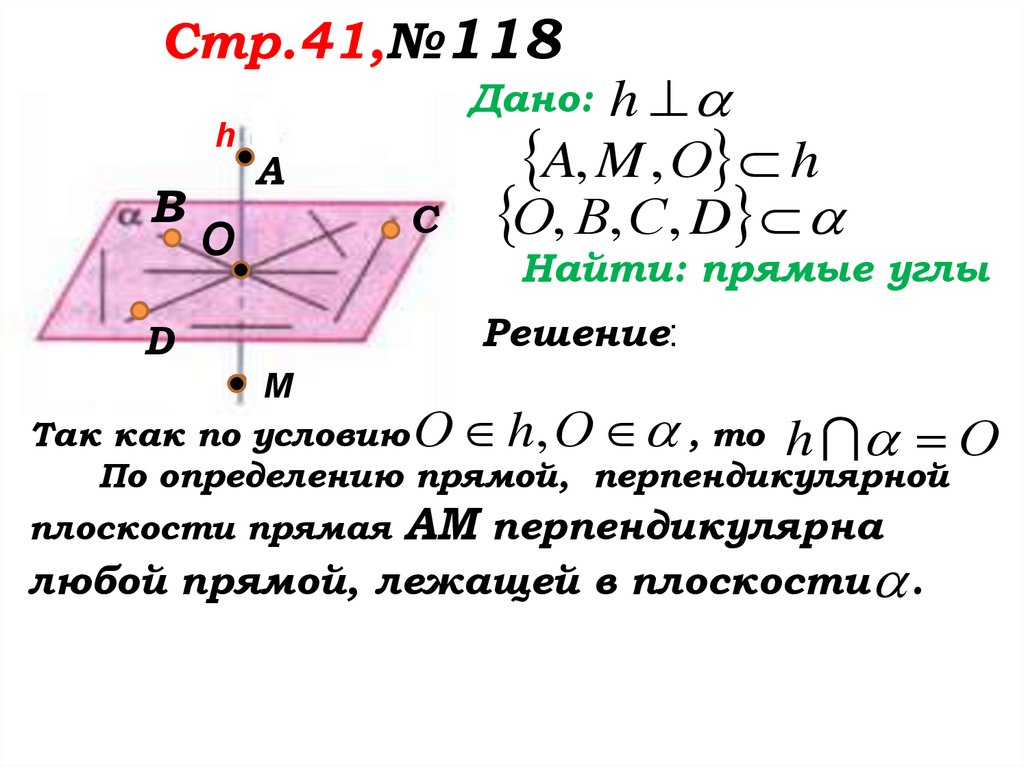
Стр.41,№118
h
В
D
О
Дано: h
А
С
A, M , О h
О, В, С, D
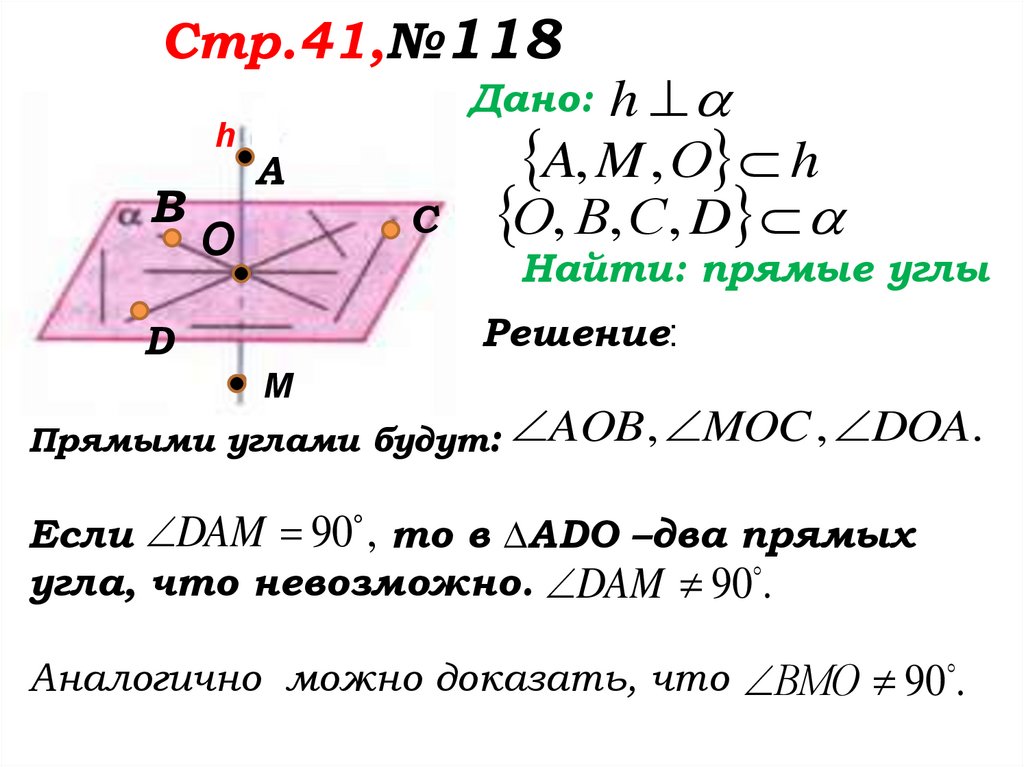
Найти: прямые углы
Решение:
М
Так как по условию О h, О , то h
О
По определению прямой, перпендикулярной
плоскости прямая АМ перпендикулярна
любой прямой, лежащей в плоскости .

5.

Стр.41,№118
h
В
Дано: h
А
С
О
A, M , О h
О, В, С, D
Найти: прямые углы
Решение:
D
М
Прямыми углами будут: AOB , MOC , DOA.
DAM
90
, то в ∆ADO –два прямых
Если
угла, что невозможно. DAM 90 .
Аналогично можно доказать, что ВMО 90 .

6.

Стр.41, №119(а)
А
B
O
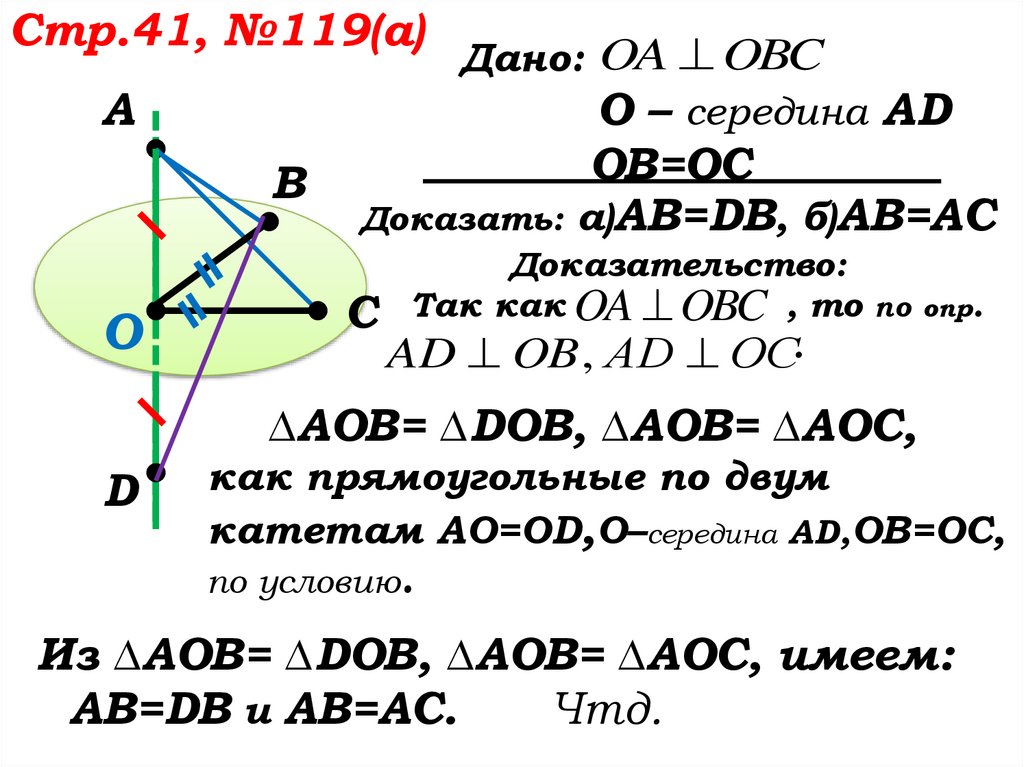
Дано: OA OBC
О – середина AD
OB=ОС
Доказать: а)AB=DB, б)АВ=АС
Доказательство:
С Так как OA OBC , то по опр.
AD OB , АD ОС.
∆АОВ= ∆DОВ, ∆АОВ= ∆АОС,
D
как прямоугольные по двум
катетам АО=ОD,О–середина AD,OB=ОС,
по условию.
Из ∆АОВ= ∆DОВ, ∆АОВ= ∆АОС, имеем:
AB=DB и АВ=АС.
Чтд.

7.

Стр.41, №119(б)
А
B
O
С
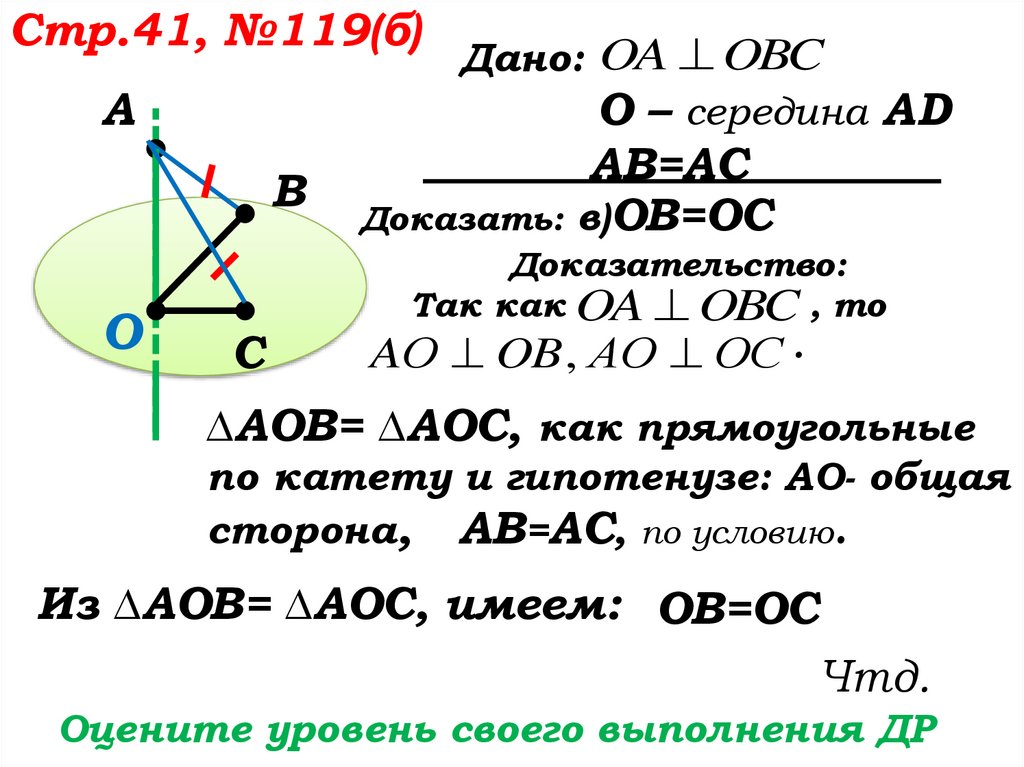
Дано: OA OBC
О – середина AD
АB=АС
Доказать: в)ОB=ОС
Доказательство:
Так как OA OBC , то
AО OB , АО ОС .
∆АОВ= ∆АОС, как прямоугольные
по катету и гипотенузе: АО- общая
сторона, АB=АС, по условию.
Из ∆АОВ= ∆АОС, имеем: ОB=ОС
Чтд.
Оцените уровень своего выполнения ДР

8.

1. Две пересекающиеся прямые
на плоскости называются
перпендикулярными
(взаимно перпендикулярными), если
они образуют … прямых угла.
Проверка

9.

Две пересекающиеся прямые на
плоскости называются
перпендикулярными
(взаимно перпендикулярными), если они
образуют четыре прямых угла.

10.

2.Две прямые в пространстве
называются перпендикулярными
(взаимно … ), если угол между
ними равен …°

11.

Две прямые в пространстве
называются
перпендикулярными
(взаимно перпендикулярными), если
угол между ними равен 90°

12.

3.Две перпендикулярные
прямые в пространстве могут
быть:
-…
-…

13.

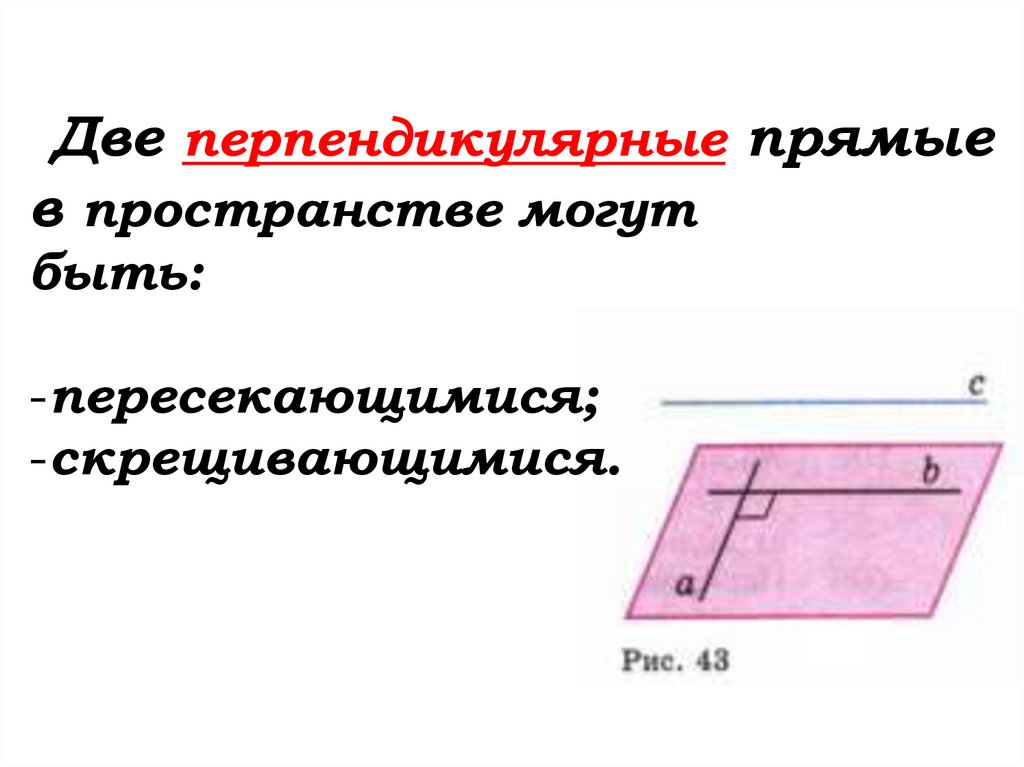
Две перпендикулярные прямые
в пространстве могут
быть:
-пересекающимися;
-скрещивающимися.

14.

4.На плоскости:
а
в
а с
с
в с
аив
…………

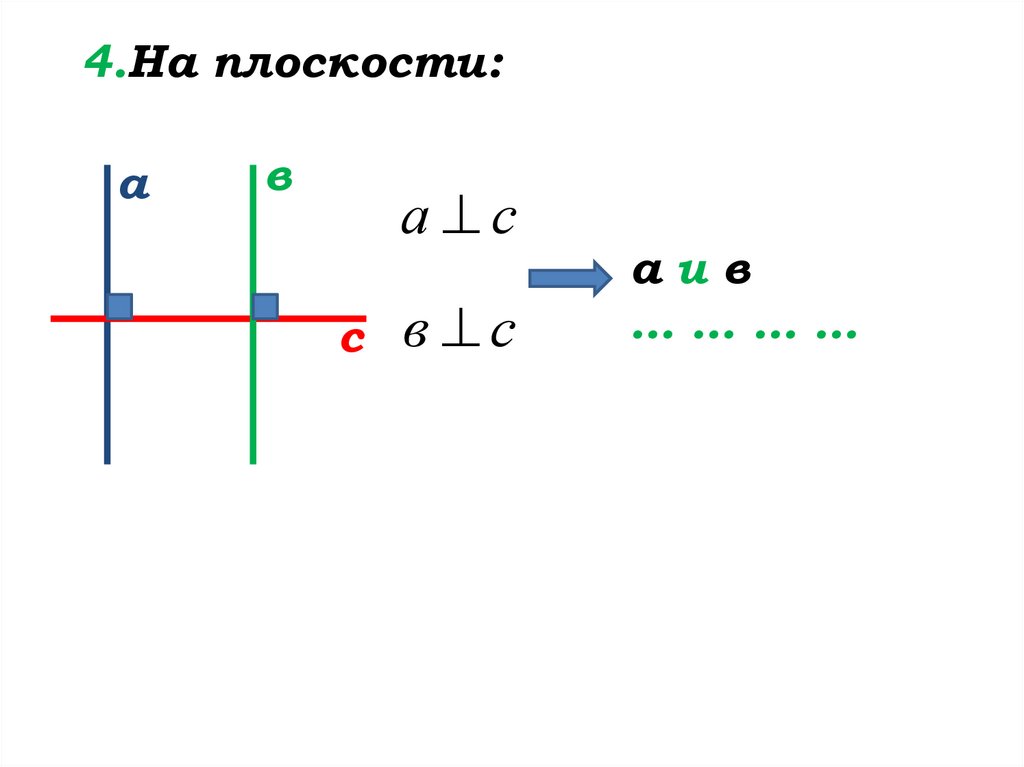
15.

На плоскости:
а
в
а с
в с
с
аив
не имеют
общих точек
Две прямые на плоскости
перпендикулярные к третьей
… ….

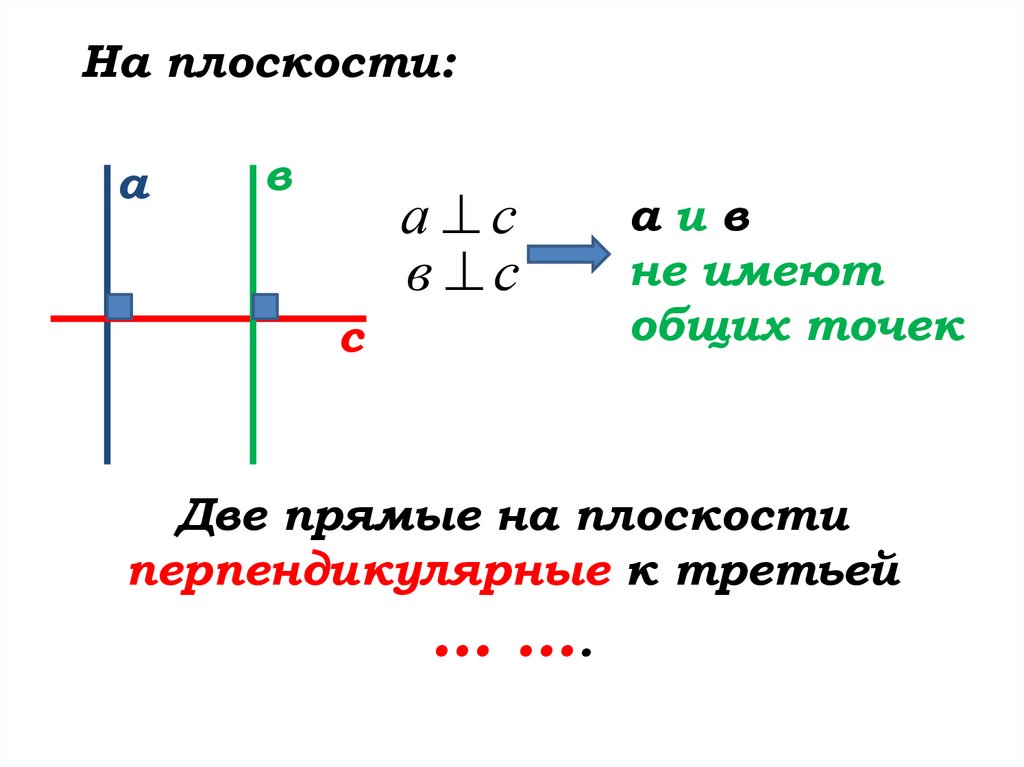
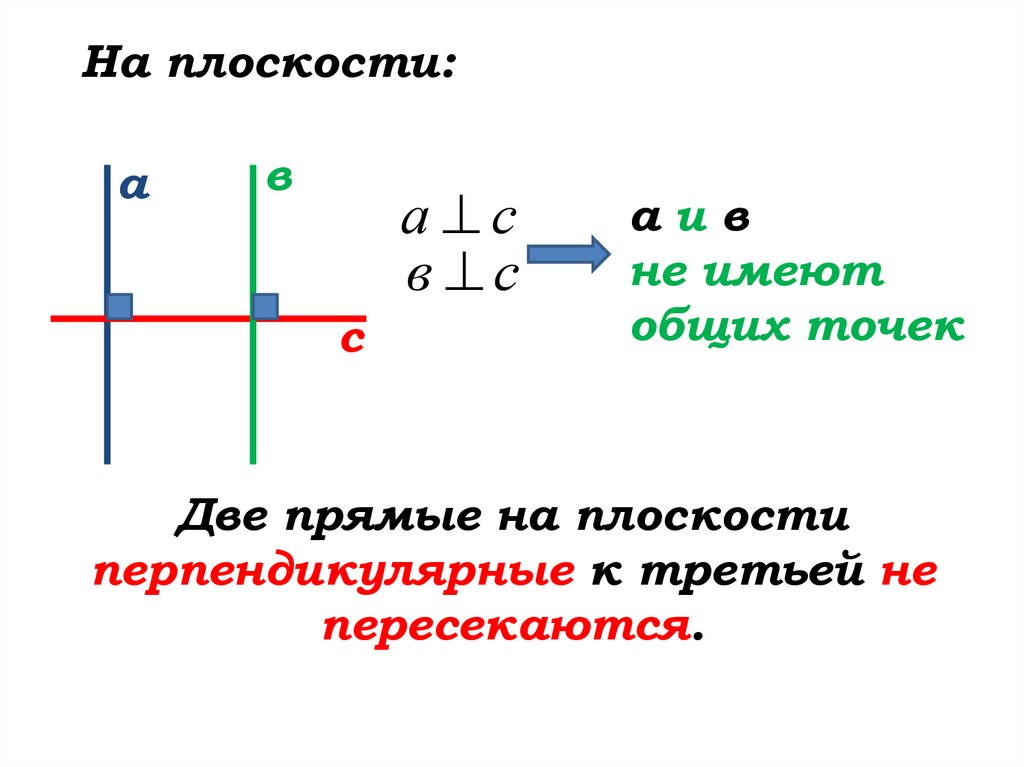
16.

На плоскости:
а
в
а с
в с
с
аив
не имеют
общих точек
Две прямые на плоскости
перпендикулярные к третьей не
пересекаются.

17.

5. Лемма: Если одна из двух
параллельных прямых
перпендикулярна к третьей прямой,
то и другая прямая
… к этой прямой
а в, а с ...

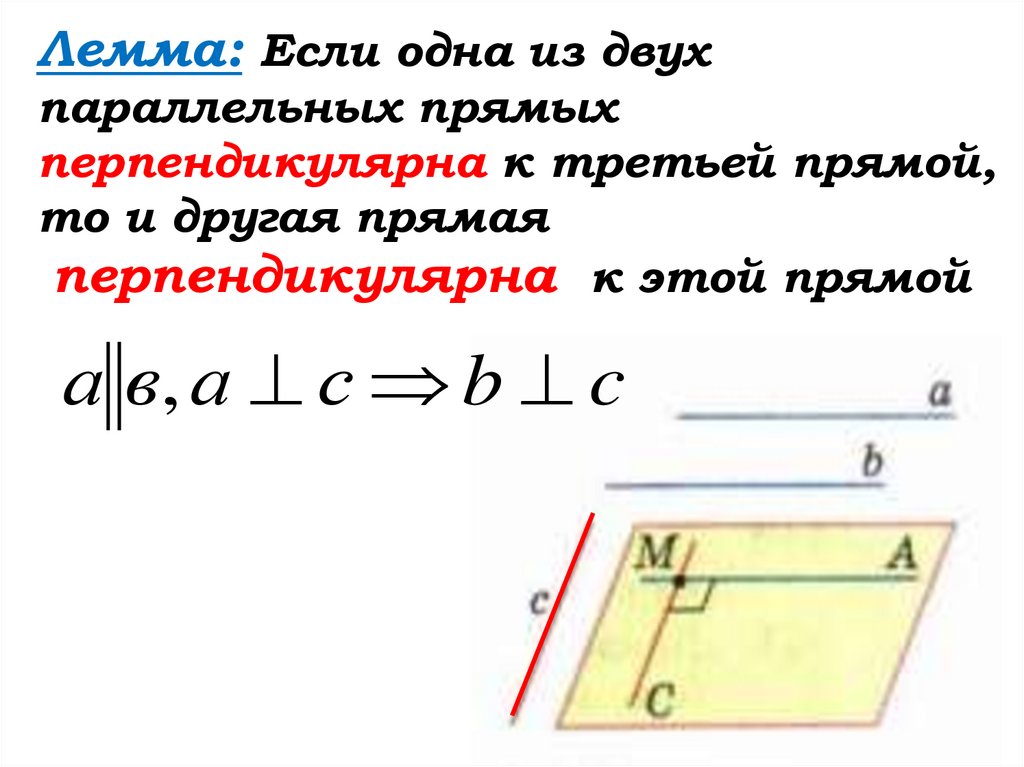
18.

Лемма: Если одна из двух
параллельных прямых
перпендикулярна к третьей прямой,
то и другая прямая
перпендикулярна к этой прямой
а в, а с b c

19.

6.Прямая называется
перпендикулярной к плоскости,
если она … к любой …, лежащей в
этой плоскости

20.

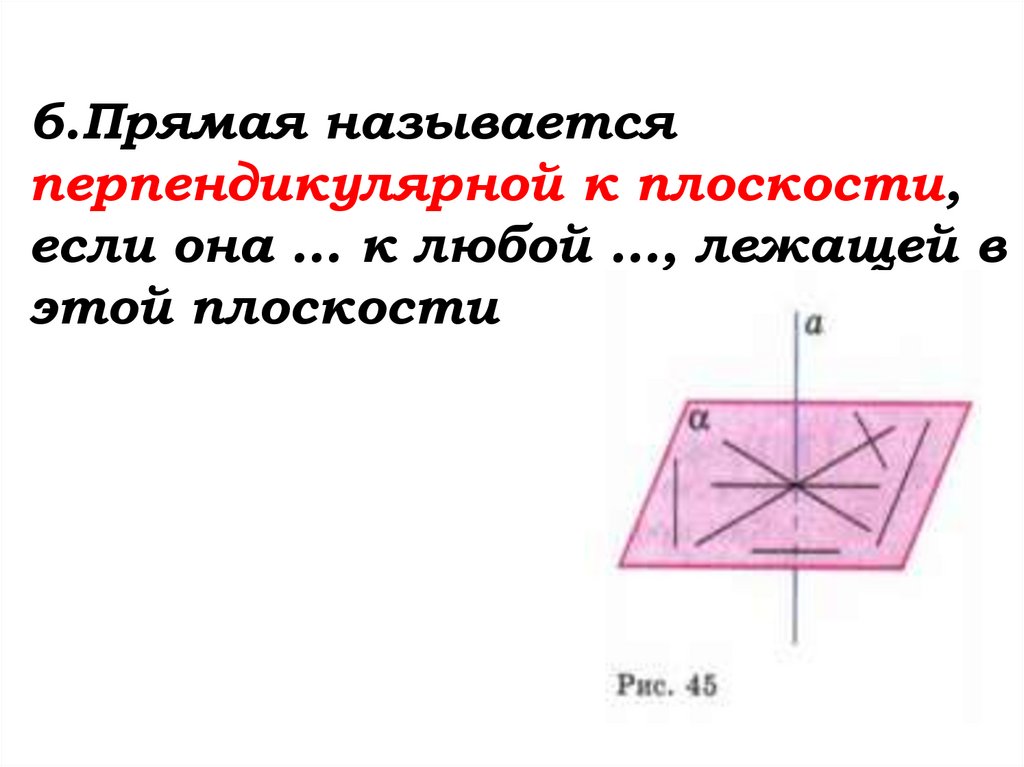
Прямая называется
перпендикулярной к плоскости, если
она перпендикулярна к любой
прямой, лежащей в этой плоскости.
Можно ли это
проверить?

21.

Прямая называется
перпендикулярной к плоскости, если
она перпендикулярна к любой
прямой, лежащей в этой плоскости .
7.Если а ,
то прямая а
… плоскость .

22.

Изучение нового материала
Прямая называется
перпендикулярной к плоскости, если
она перпендикулярна к любой
прямой, лежащей в этой плоскости .
Если а ,
то прямая а пересекает
плоскость .

23. Цели урока:

- Ввести понятие параллельных
прямых, перпендикулярных
плоскости.
-Учиться использовать
теоретические знания и
формировать практические умения
при решении задач.
-Формировать умение рассуждать и
делать правильные выводы, решать
задачи.

24.

Изучение нового материала
Теорема.
Если одна из двух параллельных
прямых перпендикулярна к
плоскости, то и другая прямая … к
этой плоскости .
a a1 ,а ...
Что дано и что
требуется доказать?

25.

Изучение нового материала
Если одна из двух параллельных
прямых перпендикулярна к
плоскости, то и другая прямая
перпендикулярна к этой плоскости .
a a1 ,а a1
Предложите свое
доказательство теоремы

26.

Изучение нового материала
Если одна из двух параллельных
прямых перпендикулярна к
плоскости, то и другая прямая
перпендикулярна к этой плоскости .
a a1 ,а a1
Читаем
доказательство по
учебнику

27.

28.

Обратная теорема.
Изучение нового материала
Если две прямые … к плоскости,
то они …
а , b ...
Что дано и что
требуется доказать?

29.

Изучение нового материала
Если две прямые перпендикулярны к
плоскости, то они параллельны.
а ,b b

30.

Стр.41, №124
Решение
задач
Прочитайте задачу.
Перечислите, что следует
записать в условие?

31.

Стр.41, №124
Решение задач
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Доказать: PQ P1Q1
Выполняем основной чертеж,
моделируем ситуацию

32.

Стр.41, №124
Решение задач
Р
Q
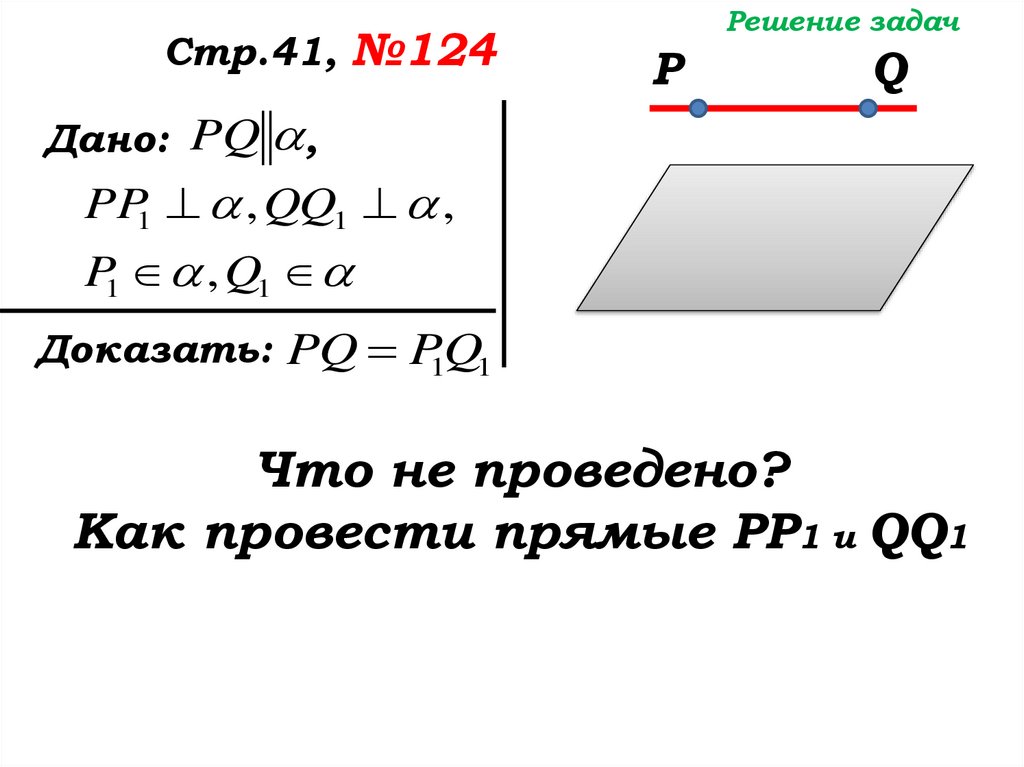
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Доказать: PQ P1Q1
Что не проведено?
Как провести прямые РР1 и QQ1

33.

Стр.41, №124
Решение задач
Р
Q
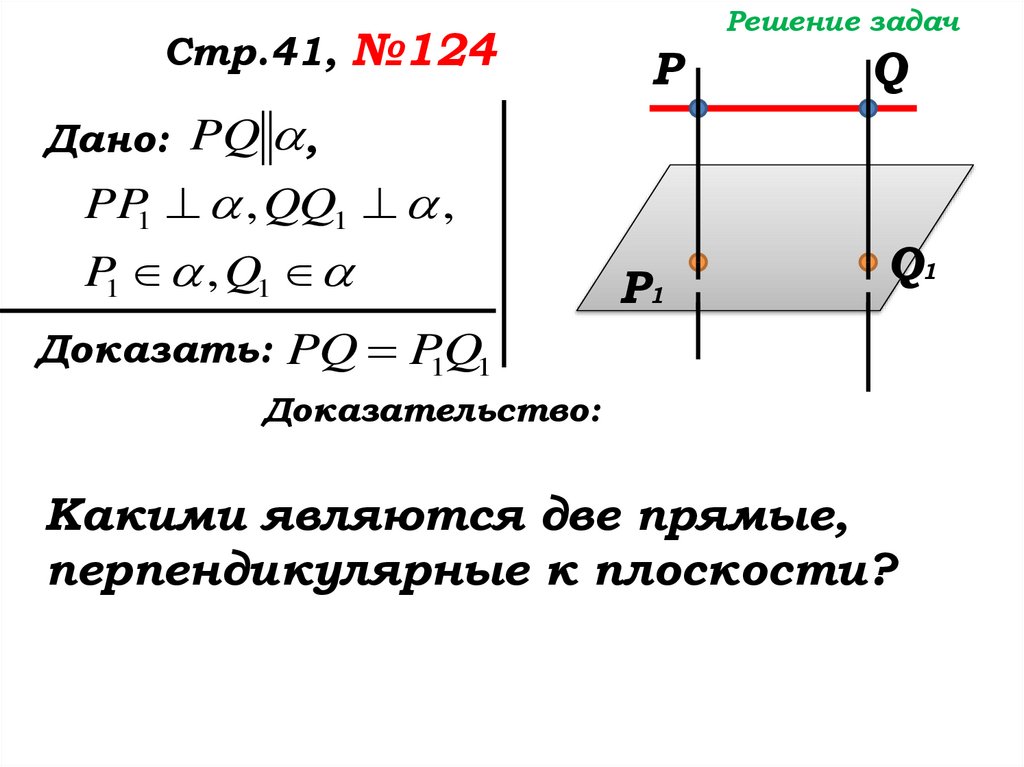
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Р1
Q1
Доказать: PQ P1Q1
Доказательство:
Какими являются две прямые,
перпендикулярные к плоскости?

34.

Стр.41, №124
Решение задач
Р
Q
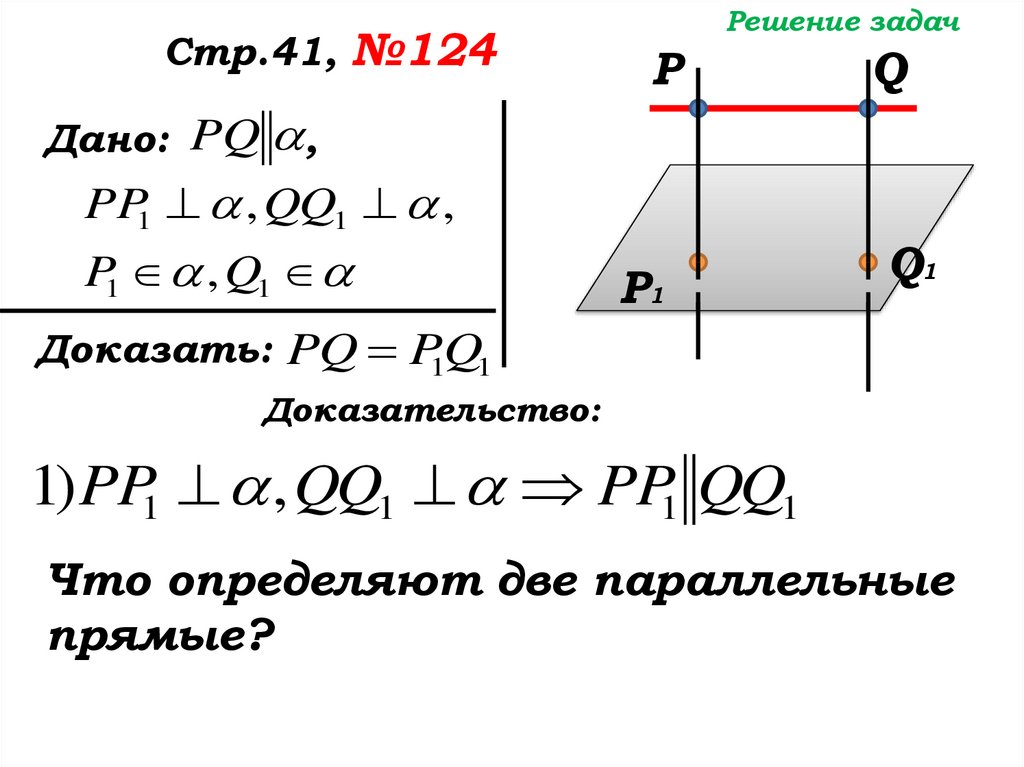
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Р1
Q1
Доказать: PQ P1Q1
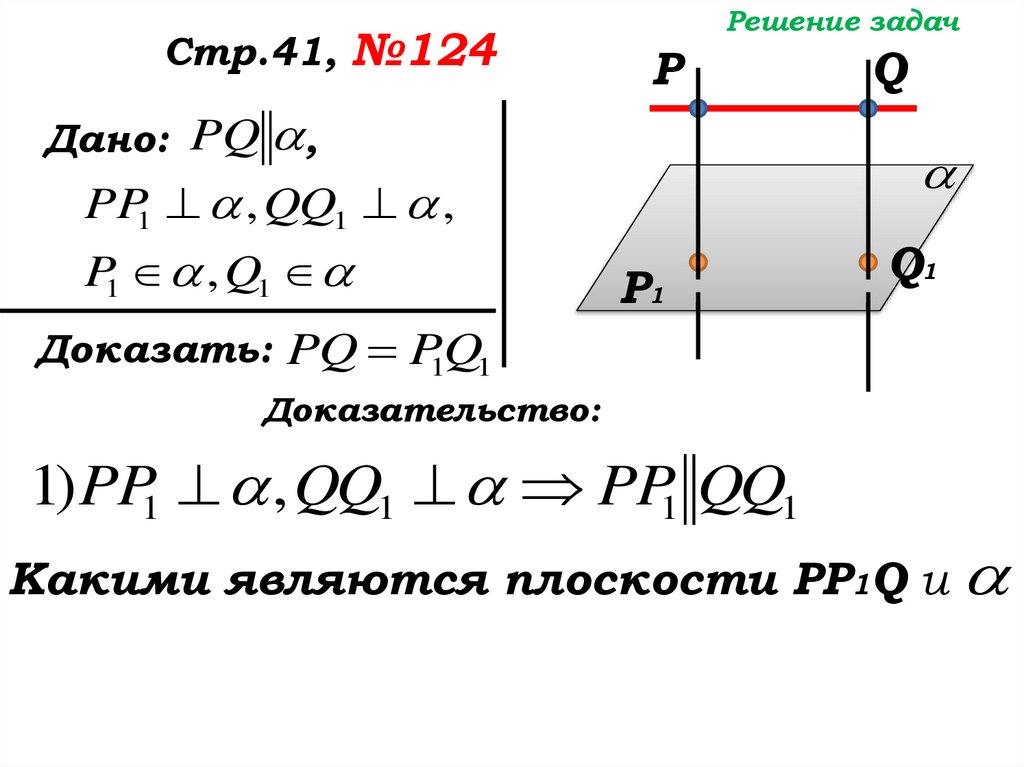
Доказательство:
1) PP1 , QQ1 PP1 QQ1
Что определяют две параллельные
прямые?

35.

Стр.41, №124
Решение задач
Р
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Q
Р1
Q1
Доказать: PQ P1Q1
Доказательство:
1) PP1 , QQ1 PP1 QQ1
Какими являются плоскости PP1Q и

36.

Стр.41, №124
Решение задач
Р
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Q
Р1
Доказать: PQ P1Q1
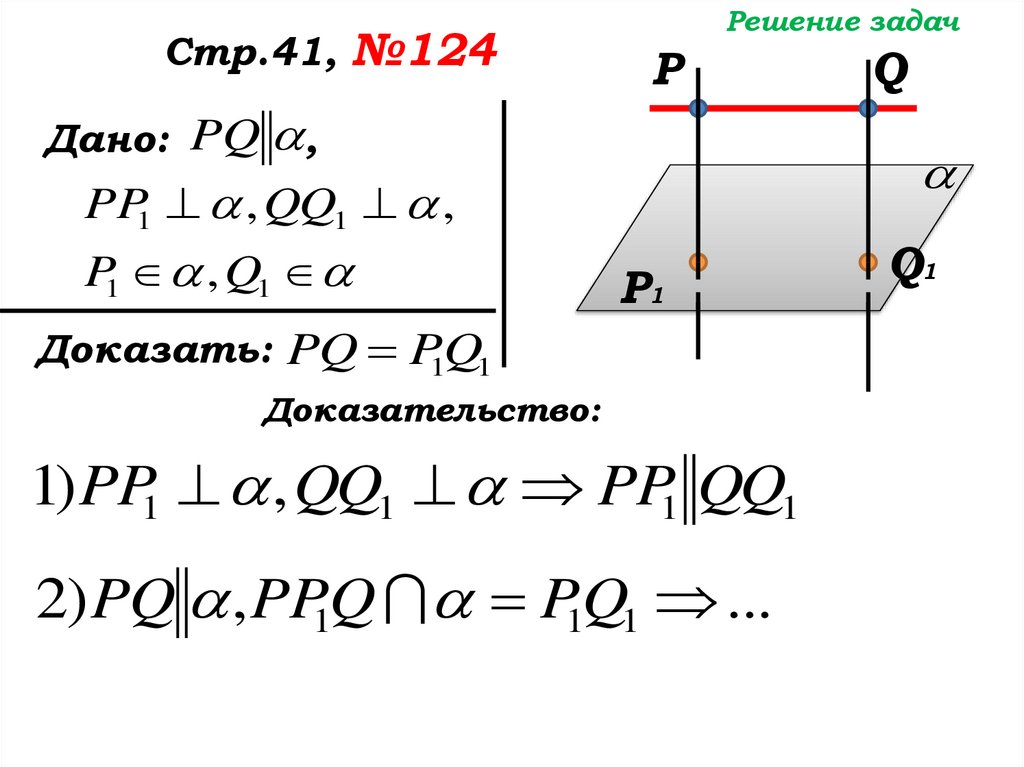
Доказательство:
1) PP1 , QQ1 PP1 QQ1
2) PQ , PP1Q P1Q1 ...
Q1

37.

Стр.41, №124
Решение задач
Р
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Q
Р1
Q1
Доказать: PQ P1Q1
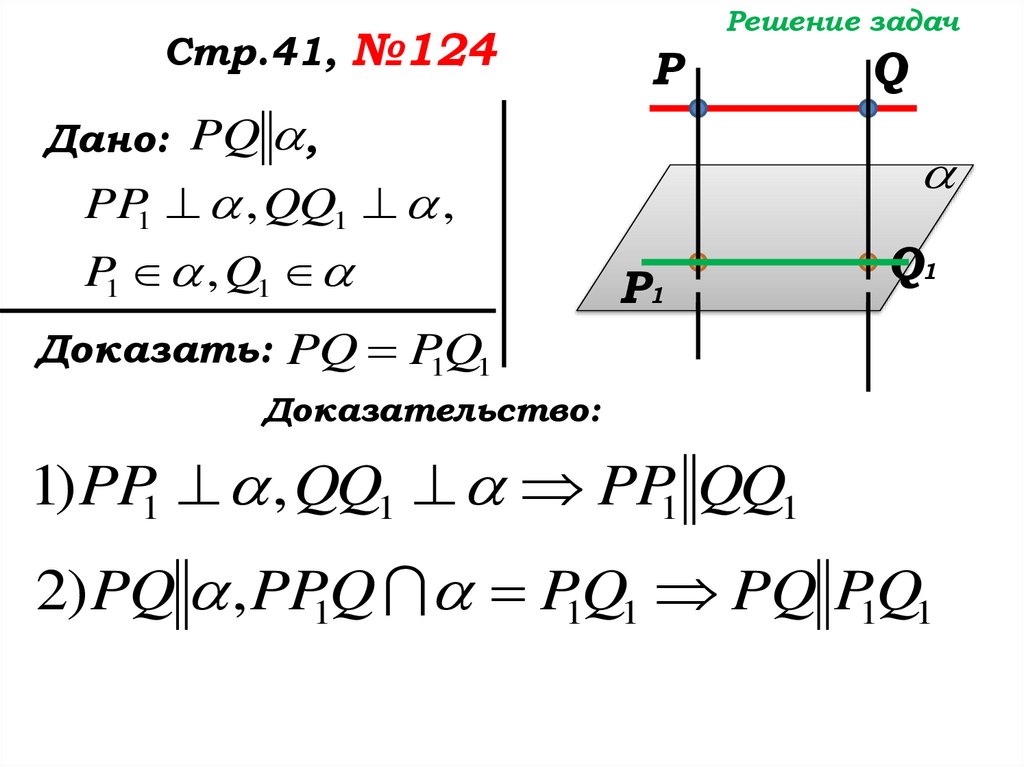
Доказательство:
1) PP1 , QQ1 PP1 QQ1
2) PQ , PP1Q P1Q1 PQ P1Q1

38.

Стр.41, №124
Решение задач
Р
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Доказать: PQ P1Q1
Q
Р1
Q1
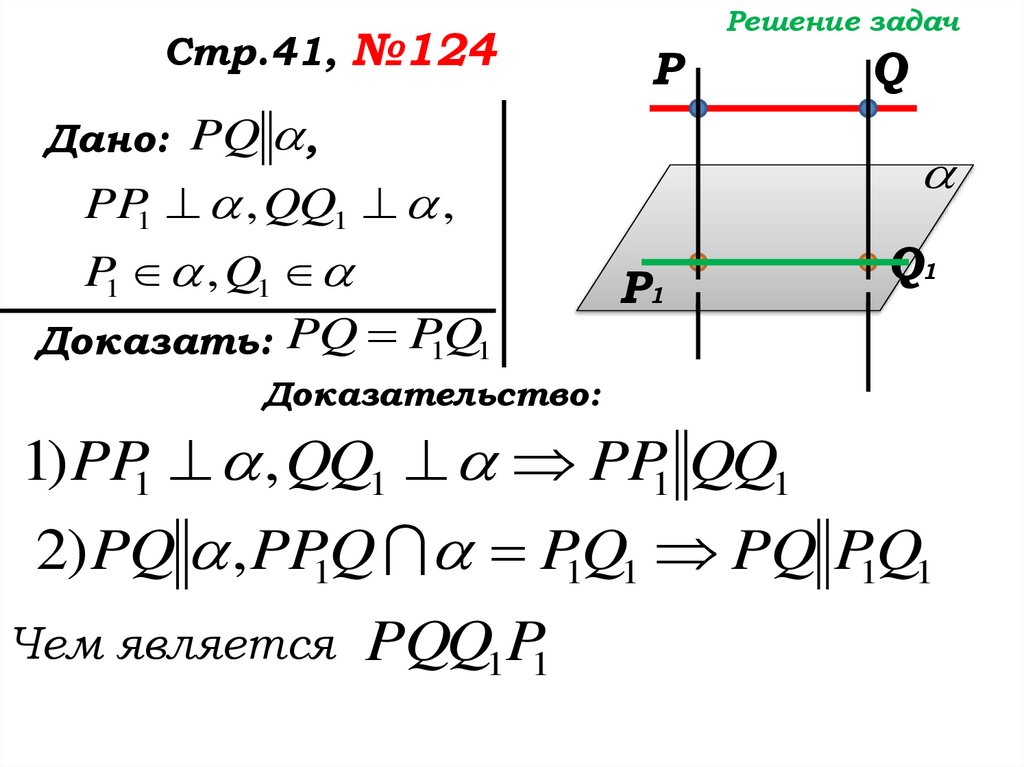
Доказательство:
1) PP1 , QQ1 PP1 QQ1
2) PQ , PP1Q P1Q1 PQ P1Q1
Чем является PQQ1P1

39.

Стр.41, №124
Решение задач
Р
Q
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Доказать: PQ P1Q1
Доказательство:
Р1
Q1
1) PP1 , QQ1 PP1 QQ1
2) PQ , PP1Q P1Q1 PQ P1Q1
3) PQQ1P1 -параллелограмм

40.

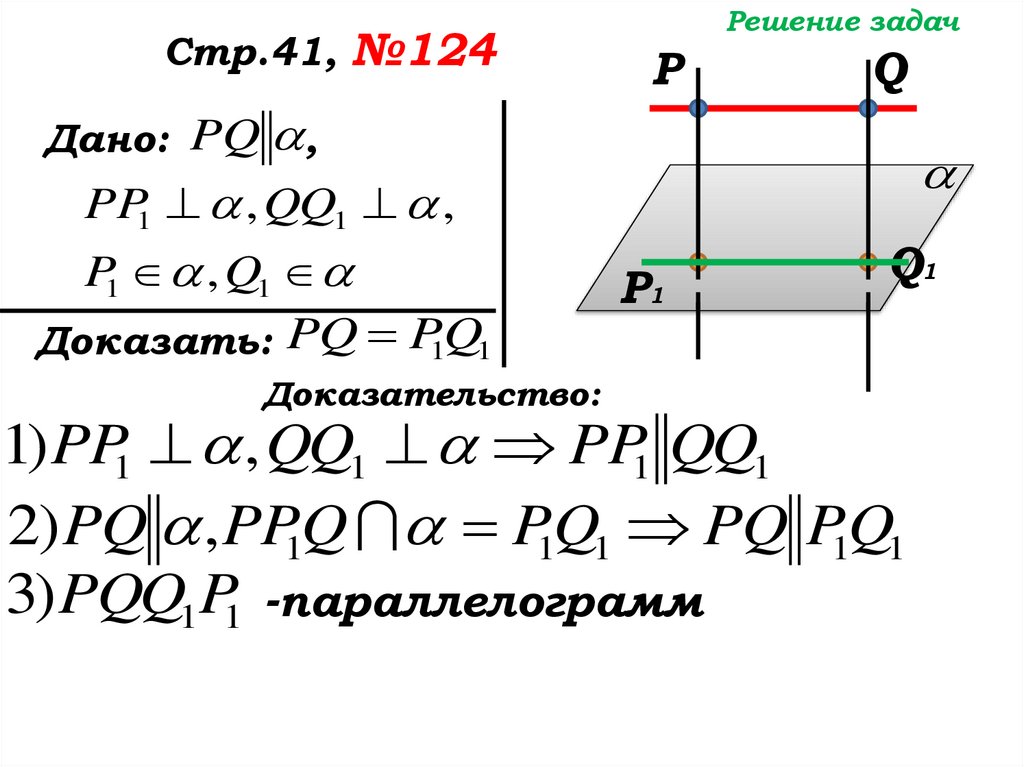
Решение задач
Стр.41, №124
Р
Q
Дано: PQ ,
PP1 , QQ1 ,
P1 , Q1
Доказать: PQ P1Q1
Q1
Р1
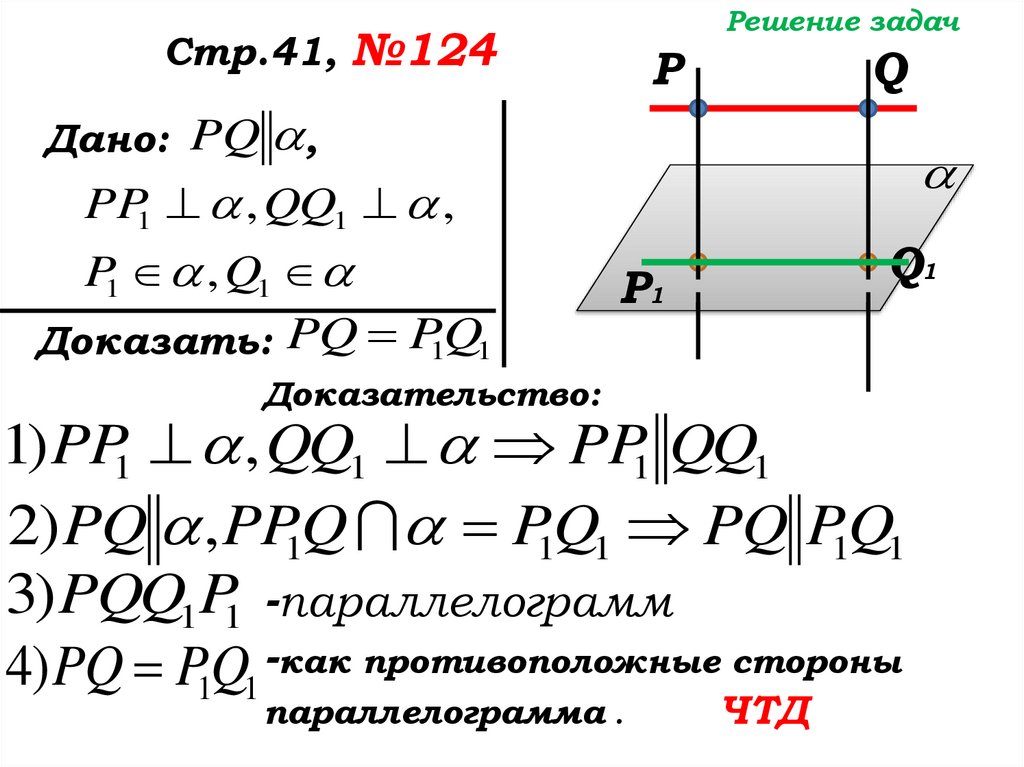
Доказательство:
1) PP1 , QQ1 PP1 QQ1
2) PQ , PP1Q P1Q1 PQ P1Q1
3) PQQ1P1 -параллелограмм
4) PQ P1Q1 -как противоположные стороны
параллелограмма .
ЧТД

41.

Прямая называется
перпендикулярной к плоскости,
если она … к любой прямой,
лежащей в этой плоскости .
Удобно ли применить это
определение для решения задач в
которых нужно показать
перпендикулярность прямой и
плоскости?

42.

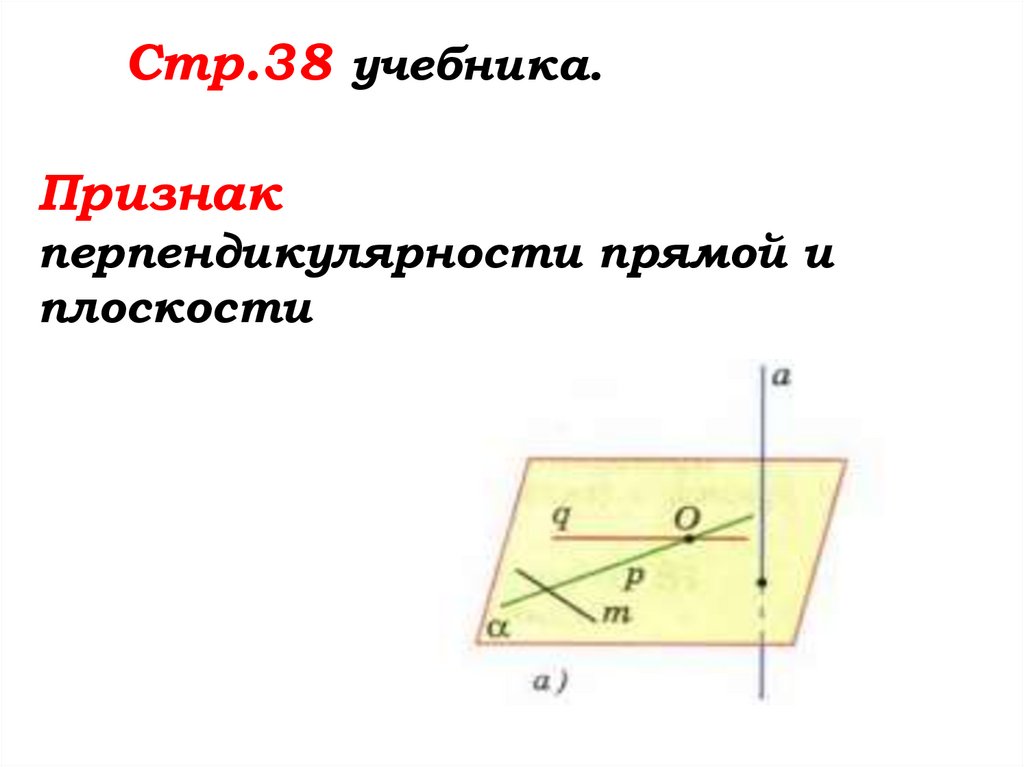
Стр.38 учебника.
Признак
перпендикулярности прямой и
плоскости

43.

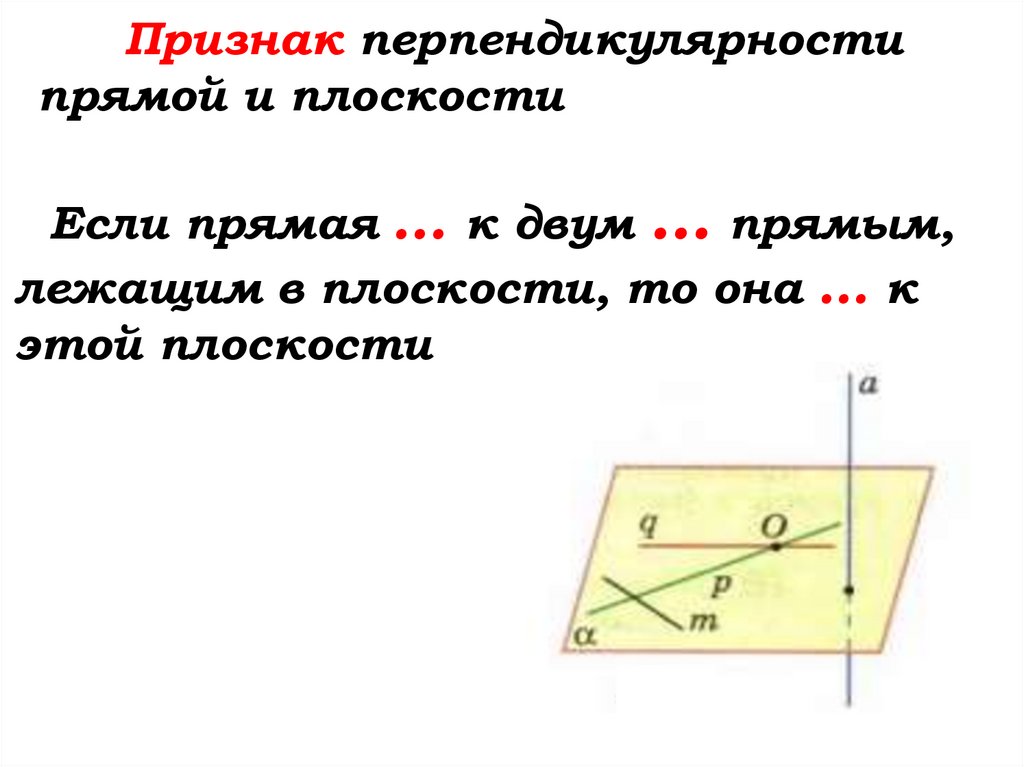
Признак перпендикулярности
прямой и плоскости
Если прямая … к двум … прямым,
лежащим в плоскости, то она … к
этой плоскости

44.

Признак перпендикулярности
прямой и плоскости
Если прямая перпендикулярна к
двум пересекающимся прямым,
лежащим в плоскости, то она
перпендикулярна к этой плоскости

45.

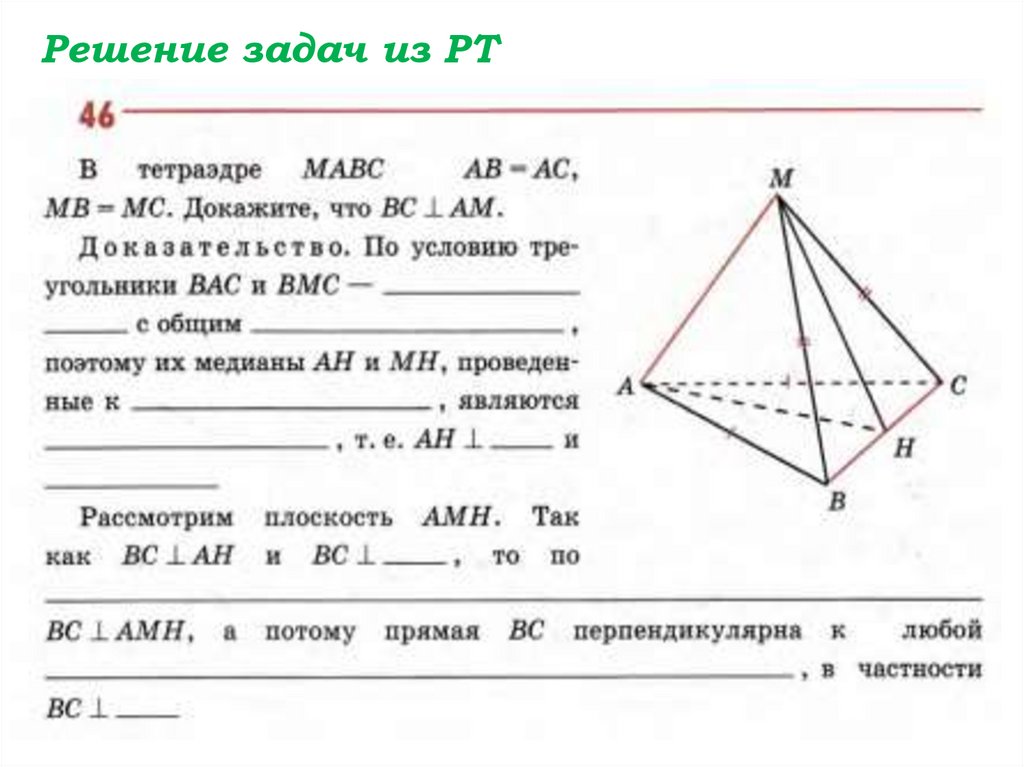
Решение задач из РТ с комментарием

46.

Решение задач из РТ

47.

Решение задач из РТ

48.

Решение задач по готовым чертежам на
слайде
АС
АМВ

49.

Решение задач по готовым чертежам
АС
АМВ
Прямая АС перпендикулярна двум …

50.

Решение задач по готовым чертежам
АС
В
Прямая АС перпендикулярна по
условию двум пересекающимся
прямым АМ и АВ плоскости АМВ, слно, по признаку перпендикулярности
прямой и плоскости,
АС перпендикулярна плоскости АМВ

51.

Решение задач по готовым чертежам
на слайде
АС
АМВ
Запишите доказательство с помощью
символов

52.

Решение задач по готовым чертежам
АС
АМВ
АС AB, АС АМ , AВ АМ А АС АМВ

53.

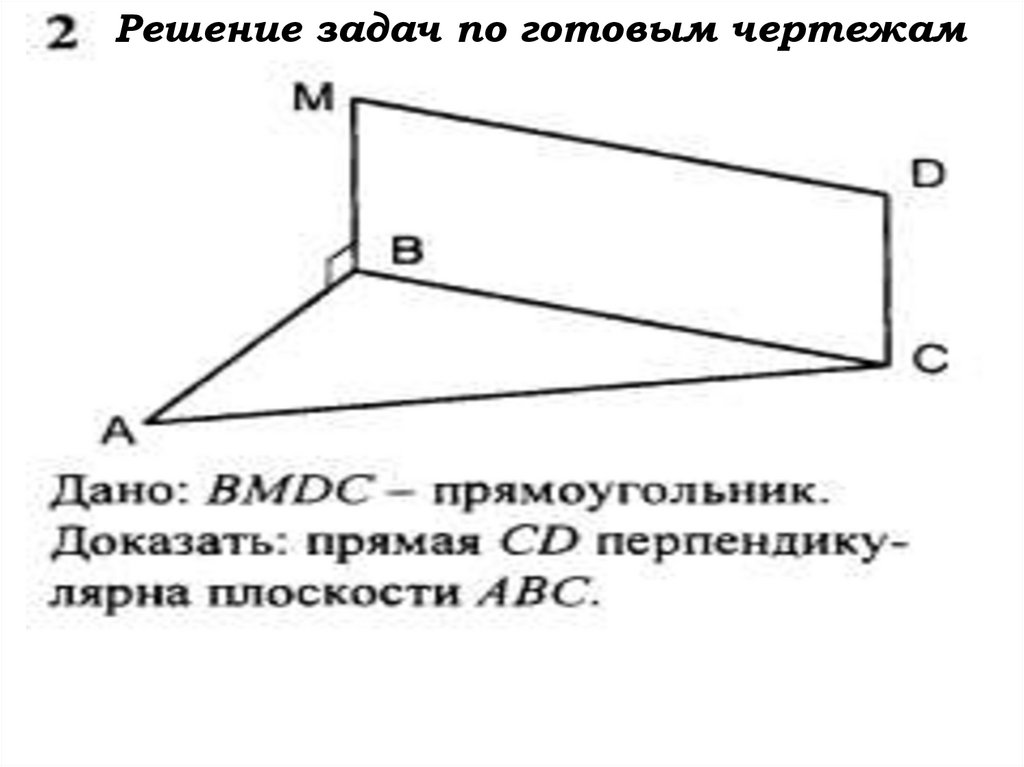
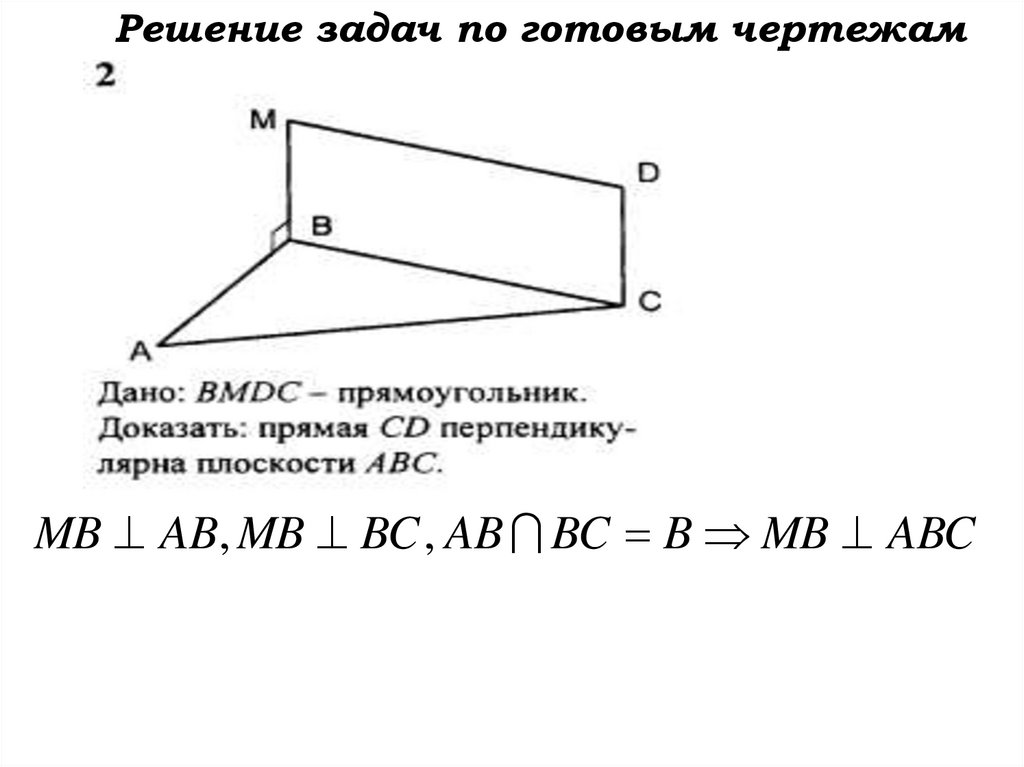
Решение задач по готовым чертежам

54.

Решение задач по готовым чертежам
MB AB, MB BC , AB BC B MB ABC

55.

Решение задач по готовым чертежам
MB AB, MB BC , AB BC B MB ABC
CD MB, MB ABC СD ABC

56.

Самостоятельное решение задач по
готовым чертежам

57.

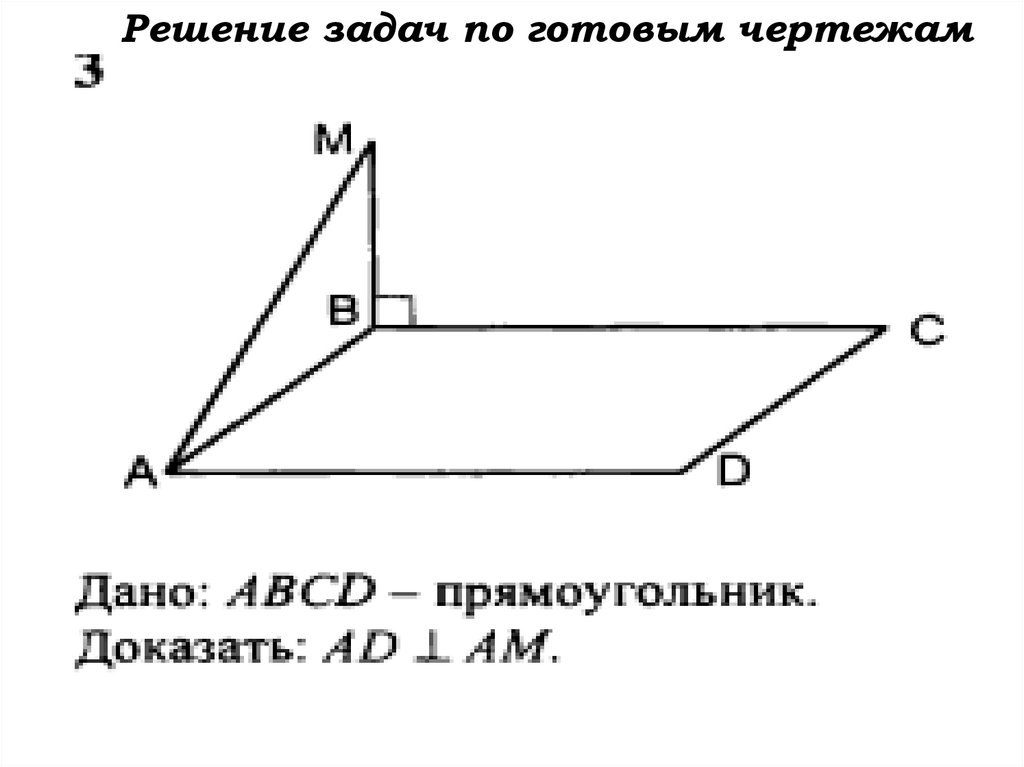
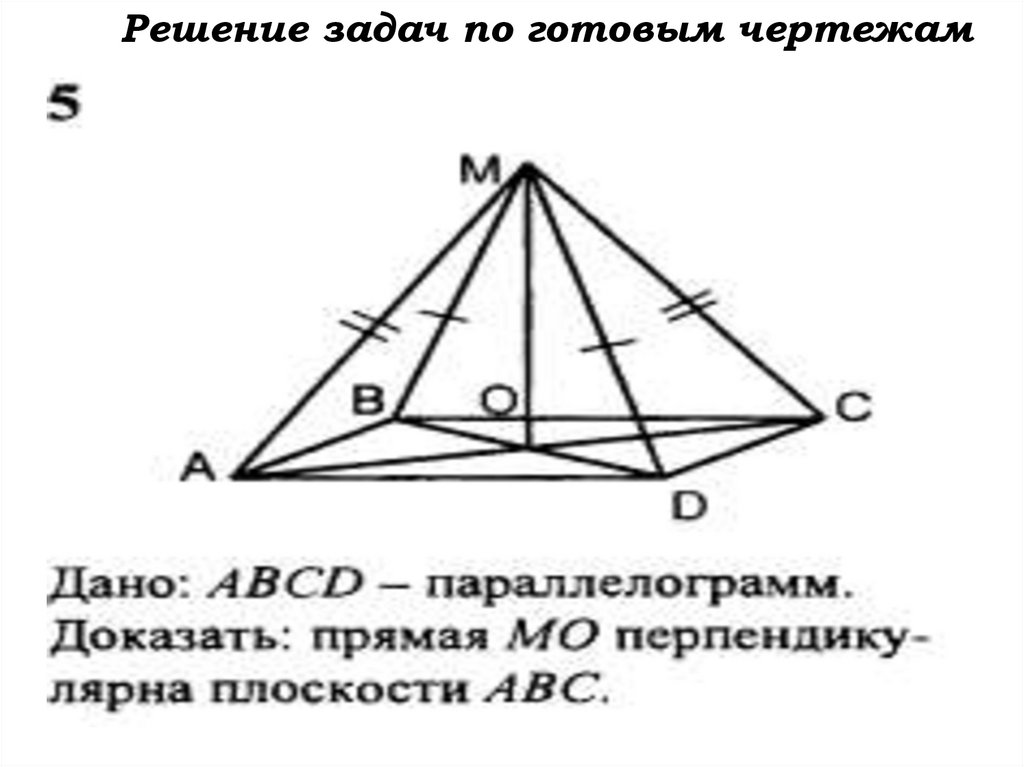
Решение задач по готовым чертежам

58.

Решение задач по готовым чертежам

59.

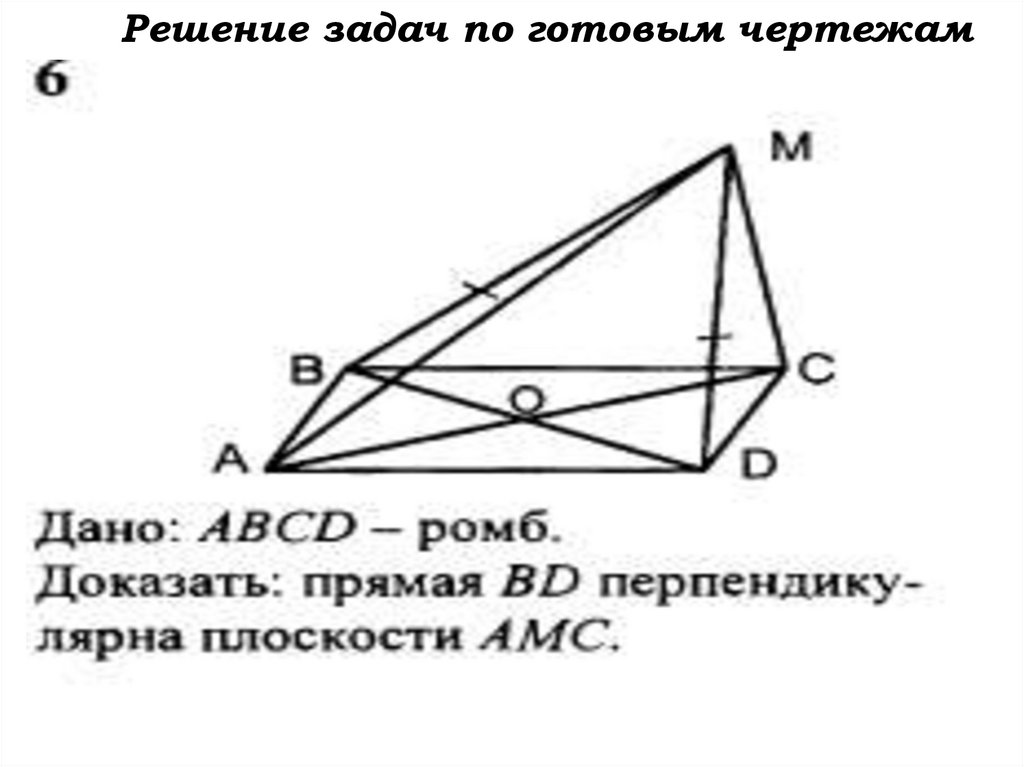
Решение задач по готовым чертежам

60.

Решение задач по готовым чертежам

61.

Вопросы 1 – 6, стр. 60

62.

Вопросы, стр. 60
C1
D1
А1
B1
С
D
А
В

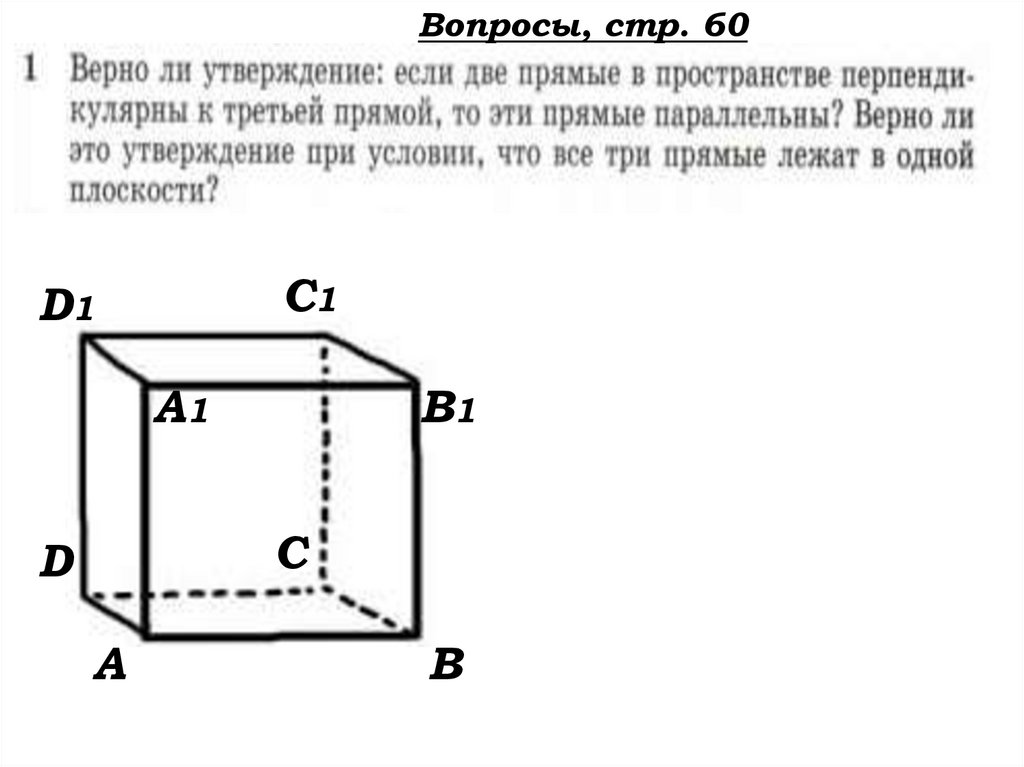
63.

Вопросы, стр. 60
C1
D1
А1
B1
С
D
А
А) Неверно,
например:
DD1 DC , BC DC
DD1 BC
б) Верно.
Если 2-е прямые на
плоскости
В перпендикулярны третьей
прямой, то они
параллельны.

64.

Вопросы, стр. 60

65.

Вопросы, стр. 60
а) По лемме о
перпендикулярности одной из
двух параллельных прямых
третьей, утверждение
а) верно;

66.

Вопросы, стр. 60
б)

67.

Вопросы, стр. 60
б)
а
с
в
Неверно, т.к прямая а может
лежать в плоскости

68.

Вопросы, стр. 60
а
в

69.

Вопросы, стр. 60
Пусть a b, тогда
а
в
a b, a b ,
что противоречит условию,
прямая b не перпендикулярна
плоскости .
Поэтому прямые a и b не
могут быть параллельными

70.

Вопросы стр. 60
в
а
с

71.

Вопросы стр. 60
в
Если a , то в плоскости
существует по крайней
мере одна прямая с,
а
с
параллельная прямой а.
Прямая b , то есть по опр. b
перпендикулярна любой прямой,
лежащей в плоскости , в том числе
и прямой с. По лемме a c, b c b a

72.

Вопросы стр. 60
а
b

73.

Вопросы стр. 60
а
b
Такая прямая существует,
она лежит в плоскости
(значит перпендикулярна
прямой b) и перпендикулярна
прямой а

74.

Вопросы, стр. 60

75.

Вопросы, стр. 60
Верно, так как все эти прямые
пересекают прямую, лежащую в этой
плоскости, и ей перпендикулярны. В этом
случае они являются параллельными и
лежат в одной плоскости.

76.

Д.З.
Разобрать конспект урока.
!!! (теория)
§1,пп. 15-17, 2 теоремы, признак.
Выучить теорему с
доказательством на оценку
Вопросы 1 – 6, стр. 60,