10_Статистическое машинное обучение

Особенность
◦ Недавние достижения в статистике были посвящены разработке более мощных
автоматизированных приемов в области предсказательного моделирования — как регрессии,
так и классификации. Эти приемы являются составной частью более общей методологии
статистического машинного обучения и отличаются от классических статистических методов
тем, что они управляемы данными и не стремятся описать данные линейной или иной
общей функцией.
◦ Метод K ближайших соседей, например, довольно прост: он классифицирует запись в
соответствии с тем, насколько записи схожи.
◦ Самые успешные и широко используемые приемы опираются на ансамблевое обучение
применительно к деревьям решений. Основная идея ансамблевого обучения состоит в том,
чтобы для формирования предсказания использовать много моделей в отличие от однойединственной модели. Деревья решений — это гибкий и автоматический прием,
предназначенный для того, чтобы обучаться правилам о связях между предикторными
переменными и переменными исходов. Оказывается, что комбинация ансамблевого обучения
с деревьями решений приводит к высокорезультативным стандартным приемам
предсказательного моделирования.
2

3.

K ближайших соседей
◦ Для каждой записи, которая будет классифицирована или
предсказана:
1. Найти K записей, которые имеют схожие признаки (т. е. схожие
значения предикторов).
2. Для классификации: выяснить среди этих схожих записей
мажоритарный класс и назначить этот класс новой записи.
3. Для предсказания (также именуемой KNN-регрессией): найти
среди этих схожих записей среднее и предсказать это среднее для
новой записи.
◦ k-nearest neighbors
◦ https://proglib.io/p/metod-k-blizhayshih-sosedey-k-nearest-
3

4.

Метод KNN как конструктор признаков
◦ Метод KNN получил свою популярность из-за его простоты и интуитивно понятной природы. С
точки зрения результативности, KNN как таковой обычно не конкурентоспособен по сравнению
с более изощренными приемами классификации.
◦ При подгонке моделей в практических условиях, однако, KNN может использоваться для
добавления "локального знания" в многоэтапном процессе с другими приемами
классификации.
1. KNN выполняется на данных, и для каждой записи формируется результат классификации
(либо квазивероятность класса).
2. Этот результат добавляется в качестве нового признака к записи, и затем на данных
выполняется еще один метод классификации. Исходные предикторные переменные таким
образом используются дважды. Поначалу можно засомневаться, не вызывает ли этот процесс
проблему, связанную с мультиколлинеарностью ввиду того, что некоторые предикторы
используются им дважды. Это не является проблемой, поскольку информация, включаемая в
модель второго этапа, очень локальна, получена только из нескольких соседних записей и
является поэтому не избыточной информацией, а дополнительной.
4

5.

Пример
При установлении продажной цены на дом агент по продаже
недвижимости будет основывать цену на схожих домах, которые были
недавно проданы, так называемых "продажах-аналогах". В сущности,
агенты по продаже недвижимости выполняют ручную версию KNN: глядя
на продажные цены схожих домов, они могут оценить, за что дом будет
продан. Мы можем создать новый признак для статистической модели,
которая будет имитировать профессионала в области торговли
недвижимостью путем применения KNN к недавним продажам.
Предсказываемое значение является продажной ценой, и существующие
предикторные переменные могут включать местоположение, общую
площадь в кв. футах, тип строения, размер земельного участка и
количество спален и ванных комнат. Новая предикторная переменная
(признак), которую мы добавляем посредством KNN, — это предиктор
KNN для каждой записи (аналогичной продажам-аналогам у агентов по
продаже недвижимости). Поскольку предсказываемое значение является
числовым, вместо мажоритарного голосования используется среднее K
ближайших соседей (KNN-регрессия).
5

6.

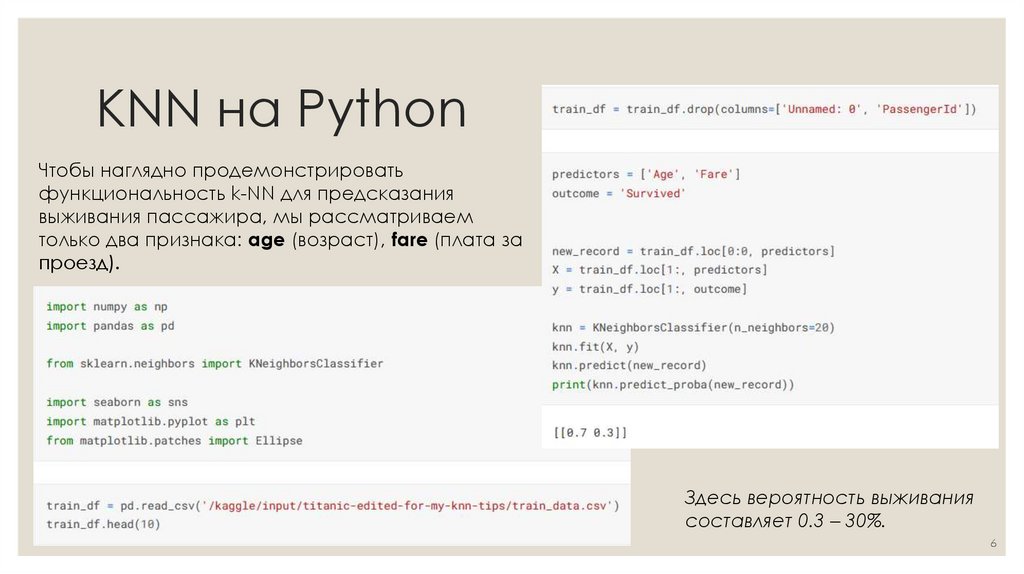
KNN на Python
Чтобы наглядно продемонстрировать
функциональность k-NN для предсказания
выживания пассажира, мы рассматриваем
только два признака: age (возраст), fare (плата за
проезд).
Здесь вероятность выживания
составляет 0.3 – 30%.
6

7.

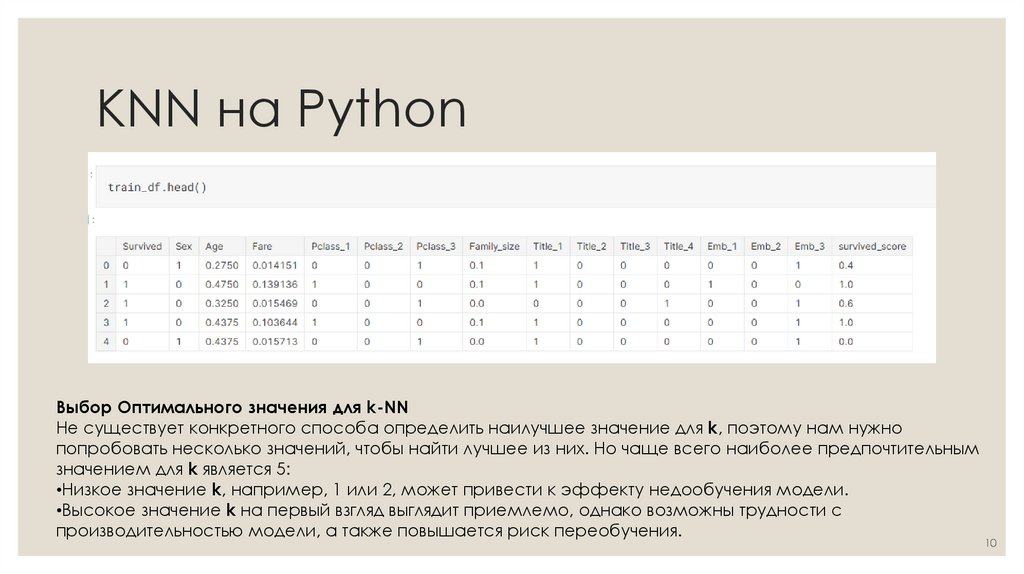
KNN на Python
Набор данных состоит из 15 столбцов, таких как
sex (пол), fare (плата за проезд), p_class (класс
каюты), family_size (размер семьи), и т. д. Главным
признаком, который мы и должны предсказать в
соревновании, является survived (выжил пассажир
или нет).
Дополнительный анализ показал, что находящиеся
в браке люди имеют больший шанс на то, чтобы
быть спасенными с корабля. Поэтому были
добавлены еще 4 столбца, переименованные из
Name (Имя), которые обозначают мужчин и
женщин в зависимости от того, были они женаты
или нет (Mr, Mrs, Mister, Miss).
7

8.

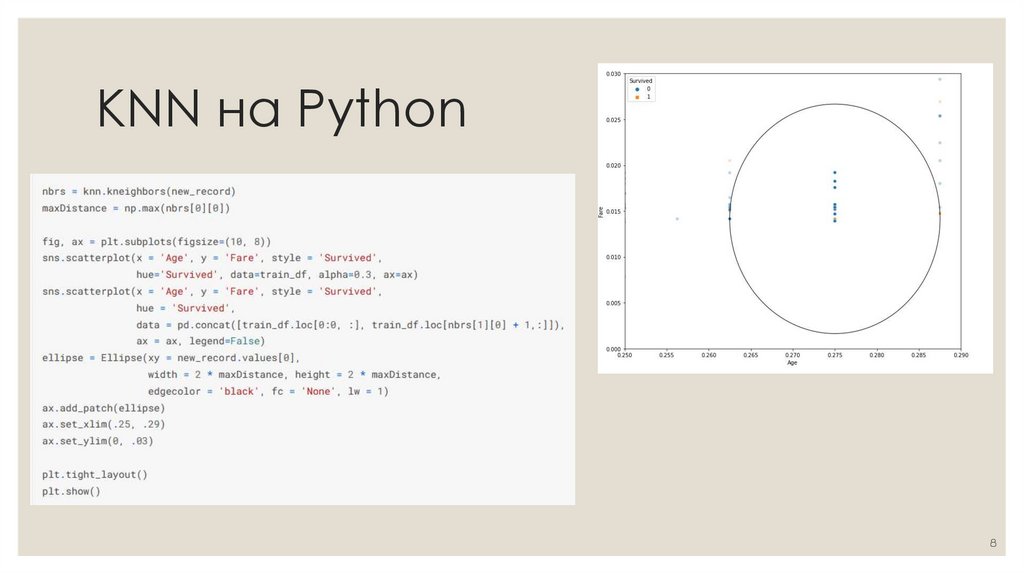
KNN на Python
8

9.

KNN на Python
9

10.

KNN на Python
Выбор Оптимального значения для k-NN
Не существует конкретного способа определить наилучшее значение для k, поэтому нам нужно
попробовать несколько значений, чтобы найти лучшее из них. Но чаще всего наиболее предпочтительным
значением для k является 5:
•Низкое значение k, например, 1 или 2, может привести к эффекту недообучения модели.
•Высокое значение k на первый взгляд выглядит приемлемо, однако возможны трудности с
производительностью модели, а также повышается риск переобучения.
10

11.

Древовидные модели
◦ Древовидные модели (классификационные и
регрессионные деревья - classification and regression
trees, CART), деревья решений, или просто деревья
— это эффективный и популярный метод
классификации (и регрессии).
◦ Древовидные модели и их более мощные потомки
случайные леса и бустинг формируют основание для
наиболее широко используемых и мощных
предсказательных инструментов моделирования в
науке о данных как для регрессии, так и для
классификации.
11

12.

Древовидная модель
◦ Древовидная модель — это набор правил импликации вида "если-то-иначе", которые
просто понять и реализовать. В отличие от регрессии и логистической регрессии, деревья
имеют способность обнаруживать скрытые шаблоны (образы, паттерны),
соответствующие сложным взаимодействиям в данных.
◦ В отличие от KNN или наивного байесовского классификатора, простые древовидные
модели могут быть выражены с точки зрения связей между предикторами, которые легко
поддаются интерпретации.
12

13.

Термины
◦ Рекурсивное сегментирование (recursive partitioning) - многократное разбиение данных на
разделы и подразделы с целью создания максимально однородных исходов в каждом итоговом
подразделе.
◦ Значение в точке разбиения (split value) - значение предиктора, которое делит записи на те, где
этот предиктор меньше и где он больше значения в точке разбиения.
◦ Узел (node) - в дереве решений или в наборе соответствующих правил ветвления узел это
графическое либо в виде правила представление значения в точке разбиения.
◦ Лист (leaf) - конец набора правил в формате "если-то", или ветвлений дерева, т. е. правила,
которые приводят к листу, обеспечивают одно из правил классификации для любой записи в
дереве.
◦ Потеря (loss) - число неправильных результатов классификации на конкретном этапе в
процессе разбиения; чем больше потерь, тем больше разнородность.
◦ Разнородность (impurity) (гетерогенность, нечистота) - степень смешанности классов в
подразделе данных (чем больше смешанность, тем больше разнородность).
◦ Подрезание (pruning) - Процесс поступательного подрезания ветвей полностью выращенного
дерева с целью снижения переподгонки.
13

14.

Дерево решений
◦ Деревья решений (DT) — это непараметрический
контролируемый метод обучения, используемый
для классификации и регрессии . Цель состоит в том, чтобы
создать модель, которая предсказывает значение целевой
переменной, изучая простые правила принятия решений,
выведенные из характеристик данных. Дерево можно
рассматривать как кусочно-постоянное приближение.
◦ Например, в приведенном ниже примере деревья решений
обучаются на основе данных, чтобы аппроксимировать
синусоидальную кривую с набором правил принятия
решений «если-то-еще». Чем глубже дерево, тем сложнее
правила принятия решений и тем лучше модель.
14

15.

Преимущества деревьев решений
◦ Просто понять и интерпретировать. Деревья можно визуализировать.
◦ Требуется небольшая подготовка данных. Другие методы часто требуют нормализации данных,
создания фиктивных переменных и удаления пустых значений. Однако обратите внимание, что этот
модуль не поддерживает отсутствующие значения.
◦ Стоимость использования дерева (т. Е. Прогнозирования данных) является логарифмической по
количеству точек данных, используемых для обучения дерева.
◦ Может обрабатывать как числовые, так и категориальные данные. Однако реализация scikit-learn
пока не поддерживает категориальные переменные. Другие методы обычно специализируются на
анализе наборов данных, содержащих только один тип переменных. См. Алгоритмы для получения
дополнительной информации.
◦ Способен обрабатывать проблемы с несколькими выходами.
◦ Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение
условия легко объяснить с помощью булевой логики. Напротив, в модели черного ящика
(например, в искусственной нейронной сети) результаты могут быть труднее интерпретировать.
◦ Возможна проверка модели с помощью статистических тестов. Это позволяет учитывать
надежность модели.
◦ Работает хорошо, даже если его предположения несколько нарушаются истинной моделью, на
основе которой были сгенерированы данные.
15

16.

Недостатки деревьев решений
◦ Обучающиеся дереву решений могут создавать слишком сложные деревья, которые плохо обобщают
данные. Это называется переобучением. Чтобы избежать этой проблемы, необходимы такие механизмы, как
обрезка, установка минимального количества выборок, необходимых для конечного узла, или установка
максимальной глубины дерева.
◦ Деревья решений могут быть нестабильными, поскольку небольшие изменения в данных могут привести к
созданию совершенно другого дерева. Эта проблема смягчается за счет использования деревьев решений в
ансамбле.
◦ Как видно из рисунка выше, предсказания деревьев решений не являются ни гладкими, ни непрерывными, а
являются кусочно-постоянными приближениями. Следовательно, они не годятся для экстраполяции.
◦ Известно, что проблема обучения оптимальному дереву решений является NP-полной с точки зрения нескольких
аспектов оптимальности и даже для простых концепций. Следовательно, практические алгоритмы обучения
дереву решений основаны на эвристических алгоритмах, таких как жадный алгоритм, в котором локально
оптимальные решения принимаются в каждом узле. Такие алгоритмы не могут гарантировать возврат глобального
оптимального дерева решений. Это можно смягчить путем обучения нескольких деревьев в учащемся ансамбля,
где функции и образцы выбираются случайным образом с заменой.
◦ Существуют концепции, которые трудно изучить, поскольку деревья решений не выражают их легко, например
проблемы XOR, четности или мультиплексора.
◦ Ученики дерева решений создают предвзятые деревья, если некоторые классы доминируют. Поэтому
рекомендуется сбалансировать набор данных перед подгонкой к дереву решений.
16

17.

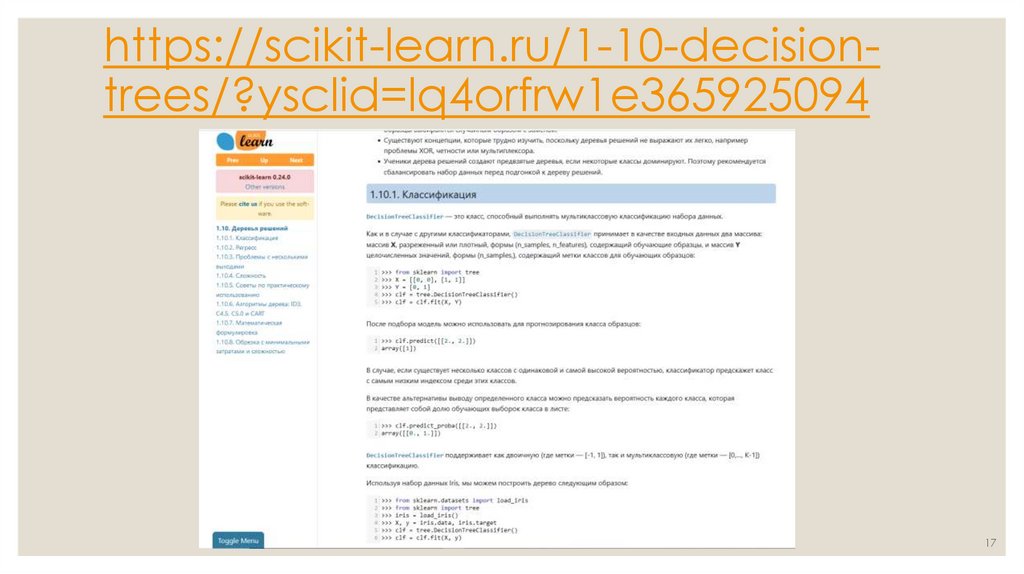
https://scikit-learn.ru/1-10-decisiontrees/?ysclid=lq4orfrw1e365925094
17

English Русский Правила