Лекция_10_Логические_основы_компьютера

1.

Логические основы
компьютеров
Логические элементы и основные
логические устройства компьютера

2.

Логические основы компьютера
Двоичная система оказалась удобной в качестве языка
логики. Это поняли спустя 100 лет после работ Буля.
С 1886 г. американский логик Чарльз
Сандерс Пирс работает над
модификацией и расширением булевой
алгебры. Пирс первый осознал, что
бинарная логика имеет сходство с работой
электрических переключательных схем.
Электрический переключатель либо
пропускает ток (истина), либо не
пропускает (ложь).
Пирс придумал простую электрическую
логическую схему, но так и не собрал ее.
(1839 - 1914)
2

3.

Логические основы компьютера
Американец Клод Шеннон –
основоположник теории информации,
разработчик теоретических основ
вычислительной техники, математик
и специалист по электронике.
Шеннон раскрыл связи между двоичным
кодированием, алгеброй логики и
электрическими схемами (релейными),
т.е. наполнил логические выражения
физическим смыслом, создал алгебру
релейных схем, на которой основана
теория бесконтактных логических
элементов.
1916 – 2001 гг.
3

4.

Логические основы компьютера
Клод Шеннон:
Принципы работы вычислительных машин в своей
основе просты.
Работа ЭВМ состоит в операциях над числами и
символами, закодированными двумя цифрами – 0 и 1,
и пересылке этой информации по линиям связи.
Работа всех устройств ЭВМ заключается в операциях
над этими последовательностями из 0 и 1.
4

5.

Логические элементы компьютера
Средством обработки двоичных сигналов в ЭВМ являются
логические элементы.
Логические элементы - это электронные схемы с одним или
несколькими входами и одним выходом, через которые проходят
электрические сигналы, представляющие цифры 0 и 1.
Для реализации любых логических операций над двоичными
сигналами достаточно элементов трех типов – элементов,
реализующих три основные логические операции: И, ИЛИ, НЕ.
Компьютер выполняет арифметические и логические операции при
помощи т.н. базовых логических элементов.
5

6.

Базовые логические элементы
Схема «И» - конъюнктор
Реализует конъюнкцию.
A
&
B
И
F
Таблица истинности
A
B
F=A B
0
0
0
0
1
0
1
0
0
1
1
1
Элемент И имеет не менее двух входов и один выход.
A, B – входные сигналы, F – выходной сигнал.
Сигнал 1 на выходе F будет сформирован тогда и только тогда,
когда на каждом из его входов будет сигнал 1. Когда хотя бы на
одном входе будет ноль, на выходе также будет ноль.
6

7.

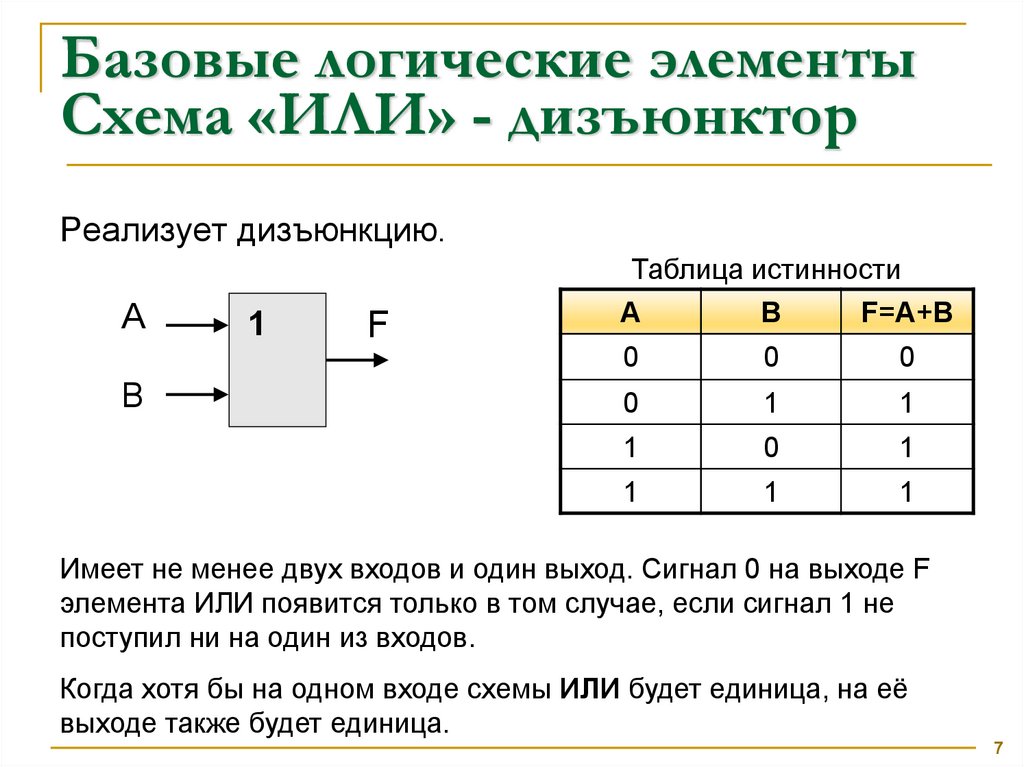
Базовые логические элементы
Схема «ИЛИ» - дизъюнктор
Реализует дизъюнкцию.
Таблица истинности
A
B
1
F
A
B
F=A+B
0
0
0
0
1
1
1
0
1
1
1
1
Имеет не менее двух входов и один выход. Сигнал 0 на выходе F
элемента ИЛИ появится только в том случае, если сигнал 1 не
поступил ни на один из входов.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на её
выходе также будет единица.
7

8.

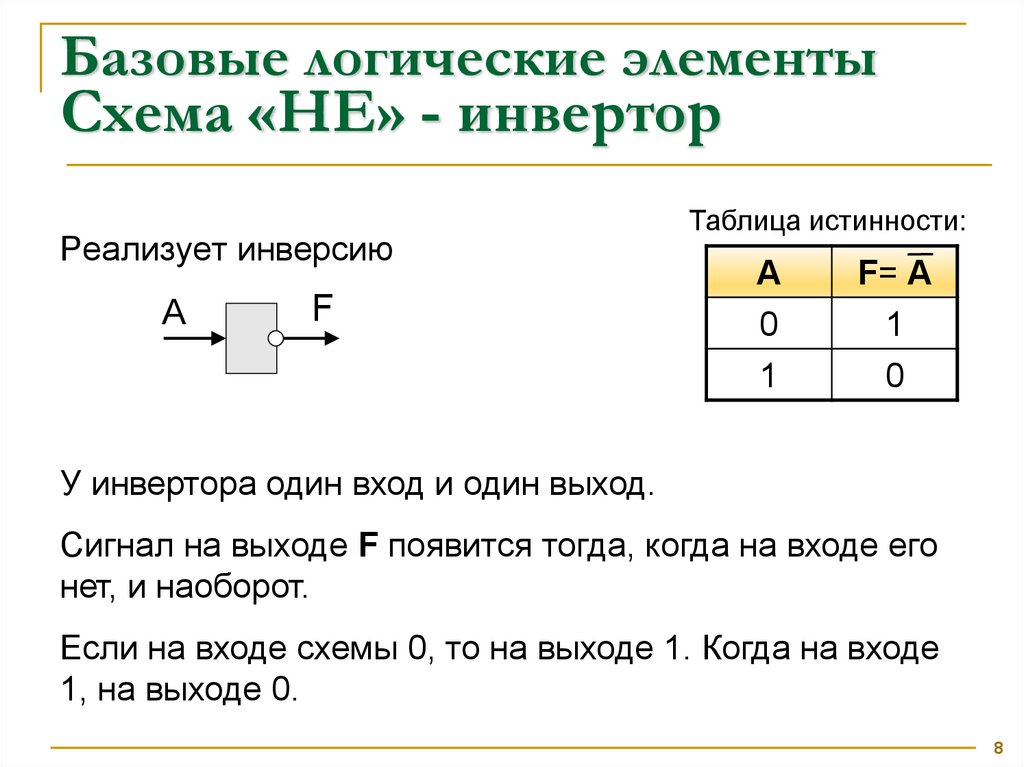
Базовые логические элементы
Схема «НЕ» - инвертор
Реализует инверсию
A
F
Таблица истинности:
A
F= A
0
1
1
0
У инвертора один вход и один выход.
Сигнал на выходе F появится тогда, когда на входе его
нет, и наоборот.
Если на входе схемы 0, то на выходе 1. Когда на входе
1, на выходе 0.
8

9.

Комбинированные логические
элементы
Базовые логические элементы в интегральных
микросхемах могут объединяться в
различных сочетаниях.
Комбинация логических элементов позволяет
создавать схемы: И-НЕ, ИЛИ-НЕ,
Исключающее ИЛИ и более сложные
конфигурации.
9

10.

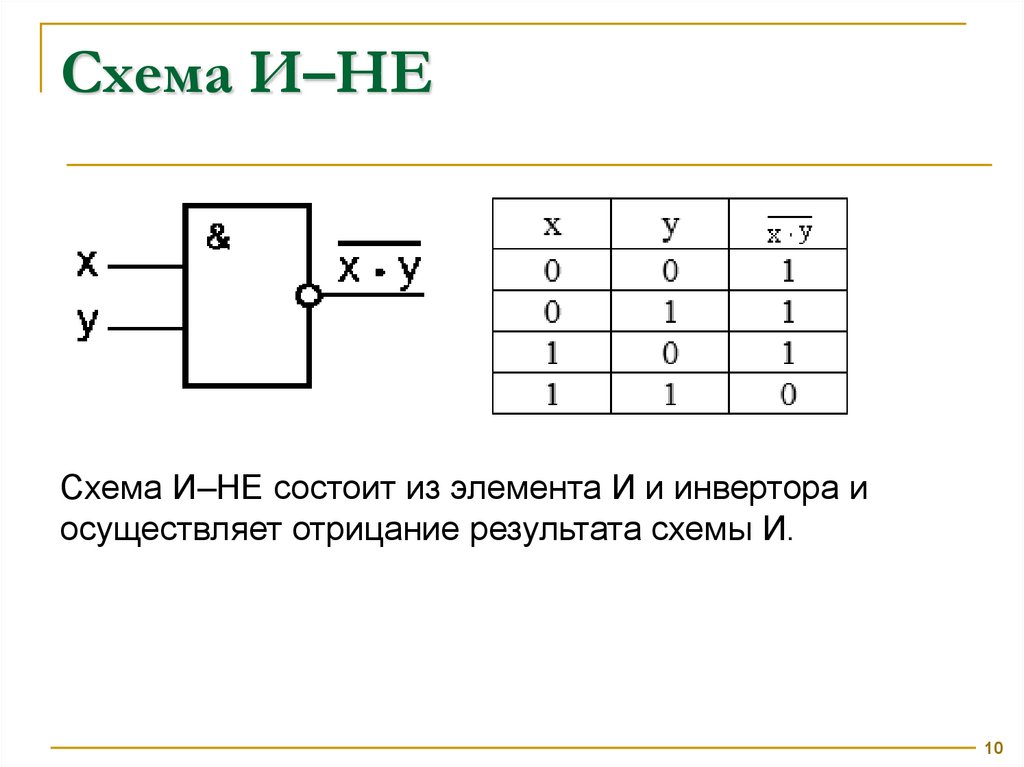
Схема И–НЕ
Схема И–НЕ состоит из элемента И и инвертора и
осуществляет отрицание результата схемы И.
10

11.

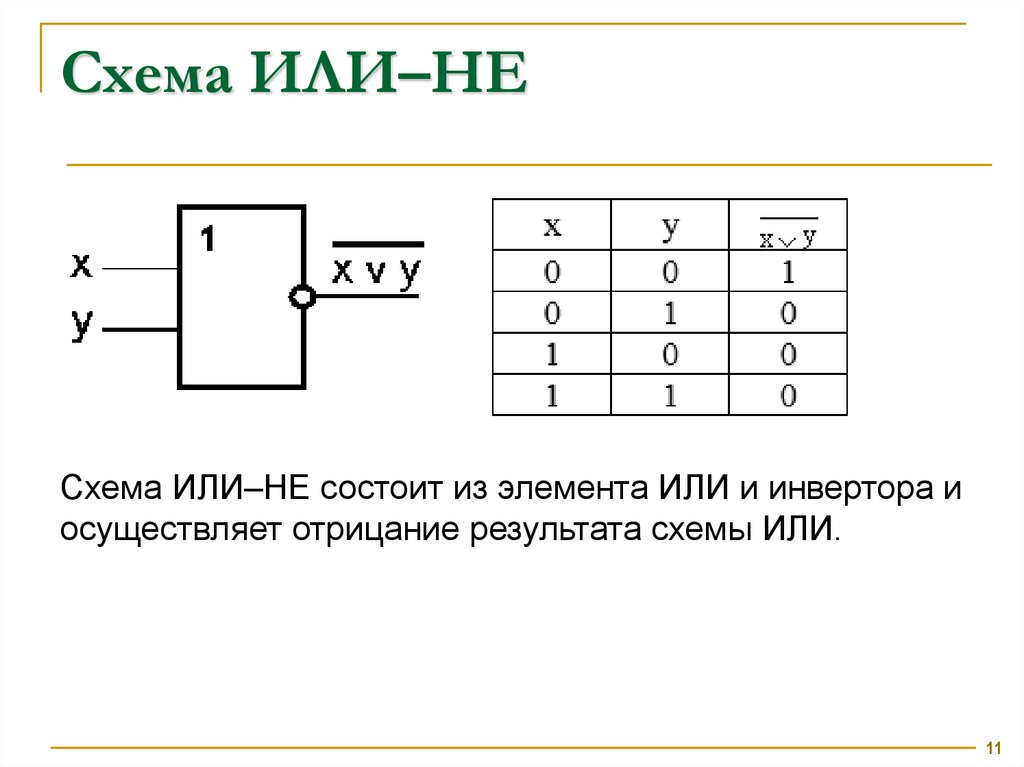
Схема ИЛИ–НЕ
Схема ИЛИ–НЕ состоит из элемента ИЛИ и инвертора и
осуществляет отрицание результата схемы ИЛИ.
11

12.

Схема Исключающее ИЛИ
Отличается от обыкновенного ИЛИ только при x = 1 и
y = 1.
Операция, которую выполняет XOR, часто называют
«сложение по модулю 2». На этих элементах строятся
цифровые сумматоры.
12

13.

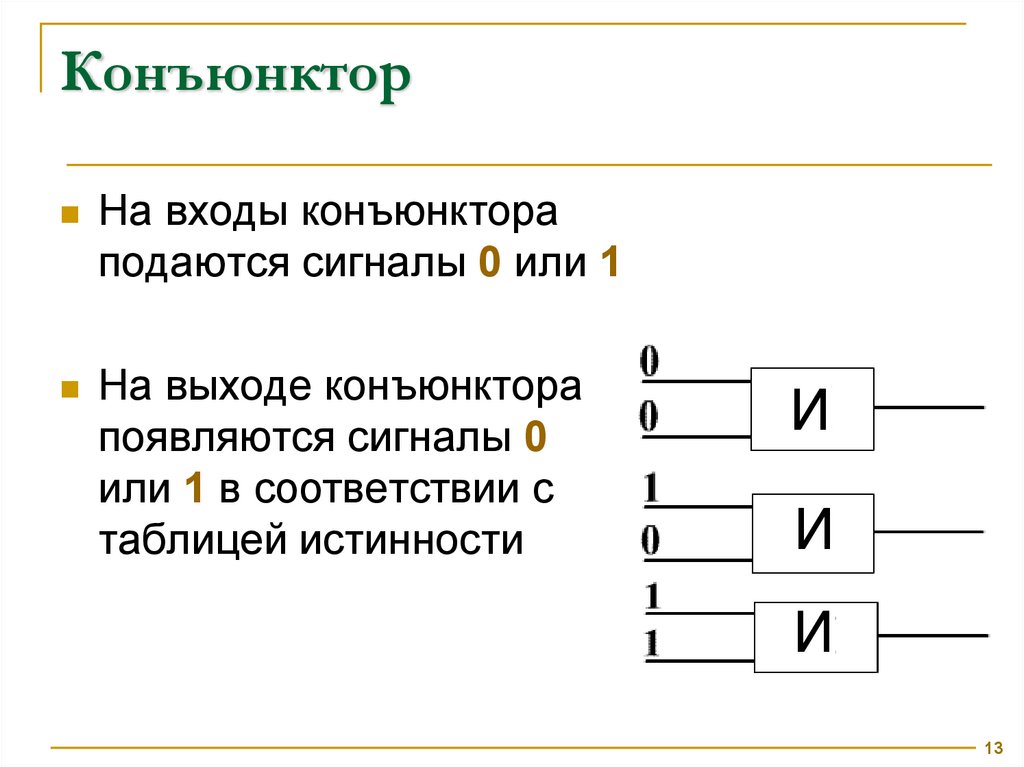
Конъюнктор
На входы конъюнктора
подаются сигналы 0 или 1
На выходе конъюнктора
появляются сигналы 0
или 1 в соответствии с
таблицей истинности
И
И
И
13

14.

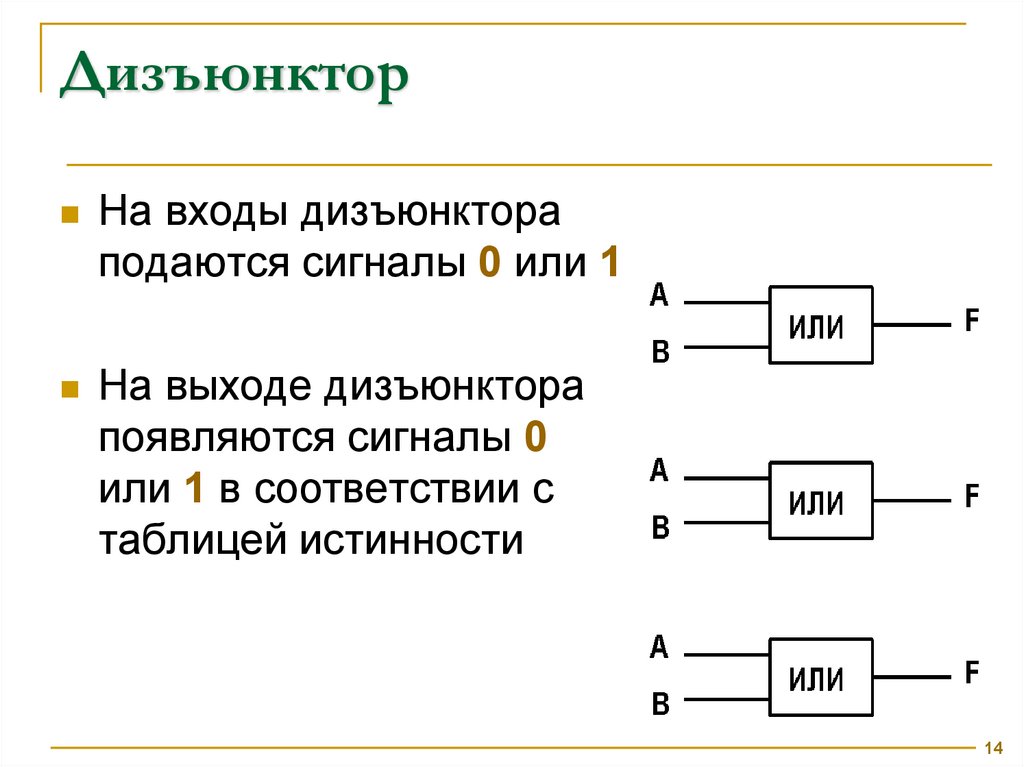
Дизъюнктор
На входы дизъюнктора
подаются сигналы 0 или 1
На выходе дизъюнктора
появляются сигналы 0
или 1 в соответствии с
таблицей истинности
14

15.

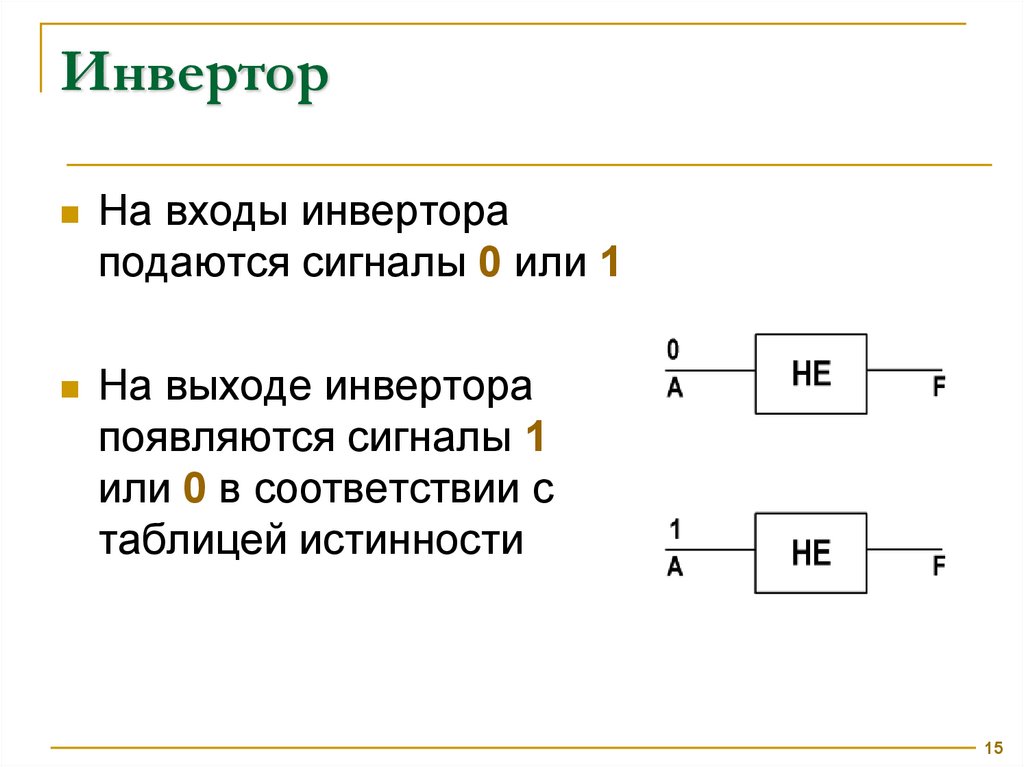
Инвеpтор
На входы инвертора
подаются сигналы 0 или 1
На выходе инвертора
появляются сигналы 1
или 0 в соответствии с
таблицей истинности
15

16.

Примеры
1. В старых елочных гирляндах лампочки включались
последовательно. Гирлянда работала тогда и только тогда,
когда все лампочки были исправны. На какую логическую
операцию это похоже?
Логическое умножение: F=А&B&C&D
2. В современных гирляндах лампочки подключены
параллельно. На какую логическую операцию это похоже?
Логическое сложение: F=АvBvCvD
3. Выключатель. Если свет не горел, то его включают, если
горел – выключают.
Инверсия
16

17.

Логические элементы компьютера
Составные элементы
Любая логическая операция может быть
представлена через конъюнкцию,
дизъюнкцию и инверсию.
Любой сколь угодно сложный элемент
компьютера может быть сконструирован
из элементарных логических схем.
17

18.

Логические элементы компьютера
Простейшие логические элементы можно реализовать
аппаратно.
Можно создать электронные устройства на
транзисторах, резисторах и т.п., каждое из которых
имеет один или два входа для подачи управляющих
напряжений и один выход, напряжение на котором
определяется соответствующей таблицей
истинности.
В электронных схемах логическому «да» («истина», или
цифра 1 в таблицах истинности) соответствует
наличие напряжения, логическому «нет» («ложь»,
или цифра 0) – его отсутствие.
18

19.

Логические элементы компьютера
С помощью элементарных логических элементов можно
реализовать (собрать как из конструктора) типовые
функциональные узлы (блоки) ЭВМ:
триггеры
сумматоры
шифраторы
регистры
счетчики
дешифраторы
В качестве характерных устройств выберем два наиболее
важных и интересных – триггер и сумматор. Первый – основа
устройств оперативного хранения информации, второй служит
для сложения чисел.
19

20.

Триггер
Триггер – это электронная схема, широко применяемая в
регистрах компьютера для надёжного запоминания
одного разряда двоичного кода. Триггер имеет два
устойчивых состояния, одно из которых соответствует
двоичной единице, а другое – двоичному нулю.
Термин триггер происходит от английского слова trigger –
защёлка, спусковой крючок.
Для обозначения этой схемы в английском языке чаще
употребляется термин flip-flop, что означает «хлопанье».
Это название указывает на способность электронной
схемы почти мгновенно переходить
(«перебрасываться») из одного электрического
состояния в другое и наоборот.
20

21.

Триггер
Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
1
1
R
вспомогательный
выход
Q
Таблица истинности
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1
0
1
сброс
Q
1 0
1 1
1
0
установка 1
0
0
запрещен
основной
выход
reset, сброс
21

22.

Сумматор
В качестве второго примера применения логических
элементов в вычислительной технике рассмотрим
устройство, называемое сумматором.
Его назначение состоит в нахождении суммы двух
двоичных чисел.
Этот узел интересен тем, что он лежит в основе
арифметического устройства ЭВМ и иллюстрирует
некоторые принципы выполнения вычислительных
операций в компьютере.
22

23.

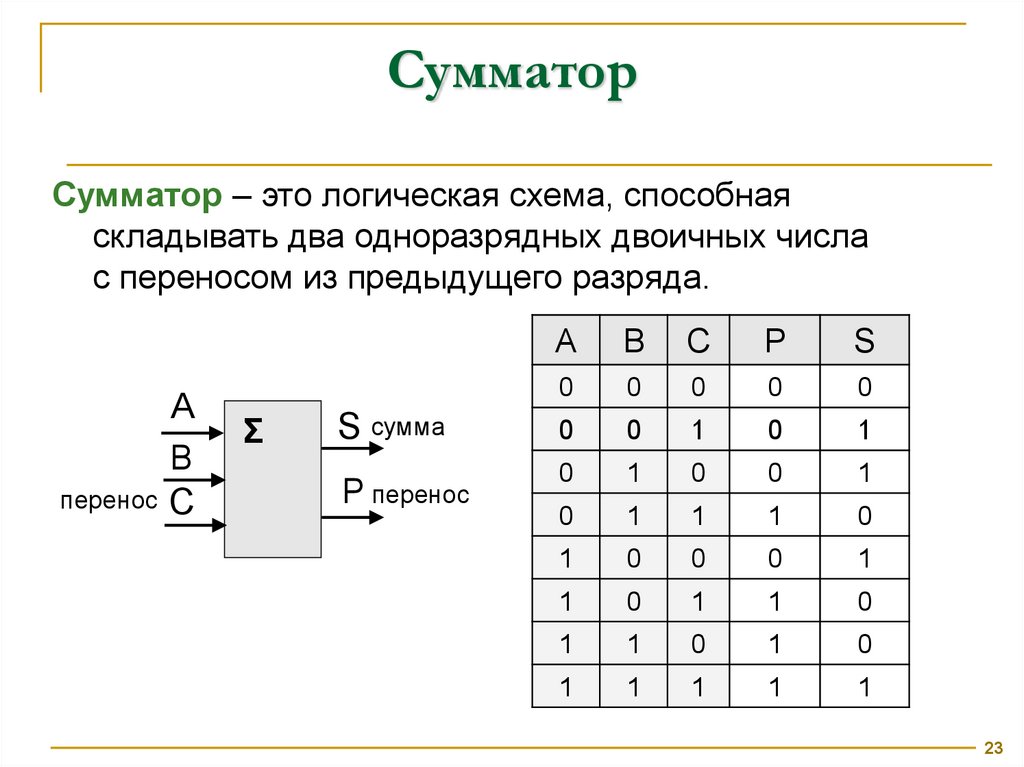
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа
с переносом из предыдущего разряда.
A
B
перенос C
Σ
S сумма
P перенос
A
B
C
P
S
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
23

24.

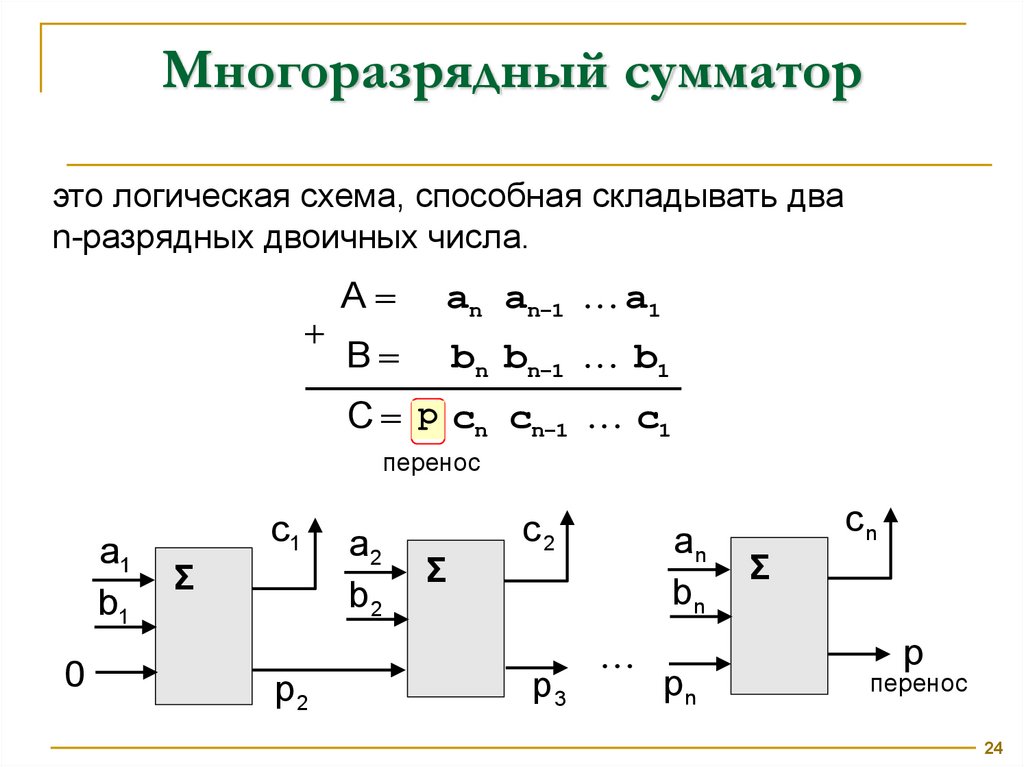
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
A
an an-1 a1
B
bn bn-1 b1
C p cn cn-1 c1
перенос
a1
b1
0
c1
Σ
p2
a2
b2
Σ
c2
p3
an
bn
pn
cn
Σ
p
перенос
24

25.

Построение логических схем по
логическому высказыванию
1) определить число простых ЛВ;
2) определить количество логических операций и их
порядок;
3) построить для каждой логической операции схему;
4) объединить логические схемы в порядке
выполнения логических операций.
25

26.

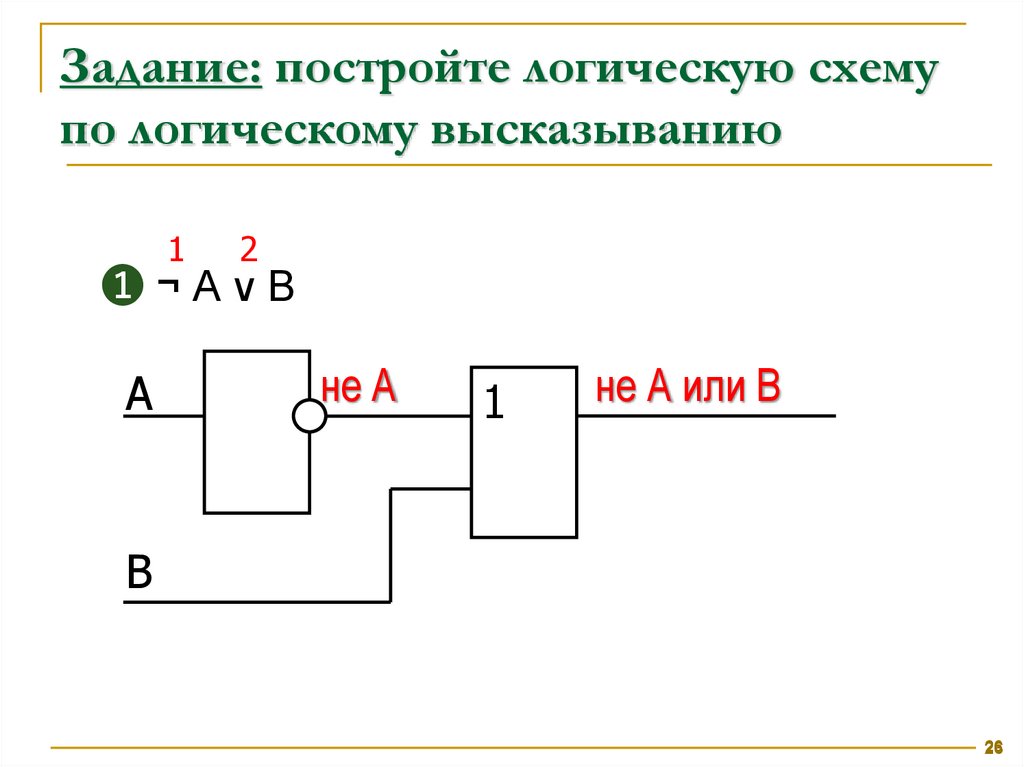
Задание: постройте логическую схему
по логическому высказыванию
1
2
➊¬AvB
A
не А
1
не А или В
В
26

27.

1
2
5
3
4
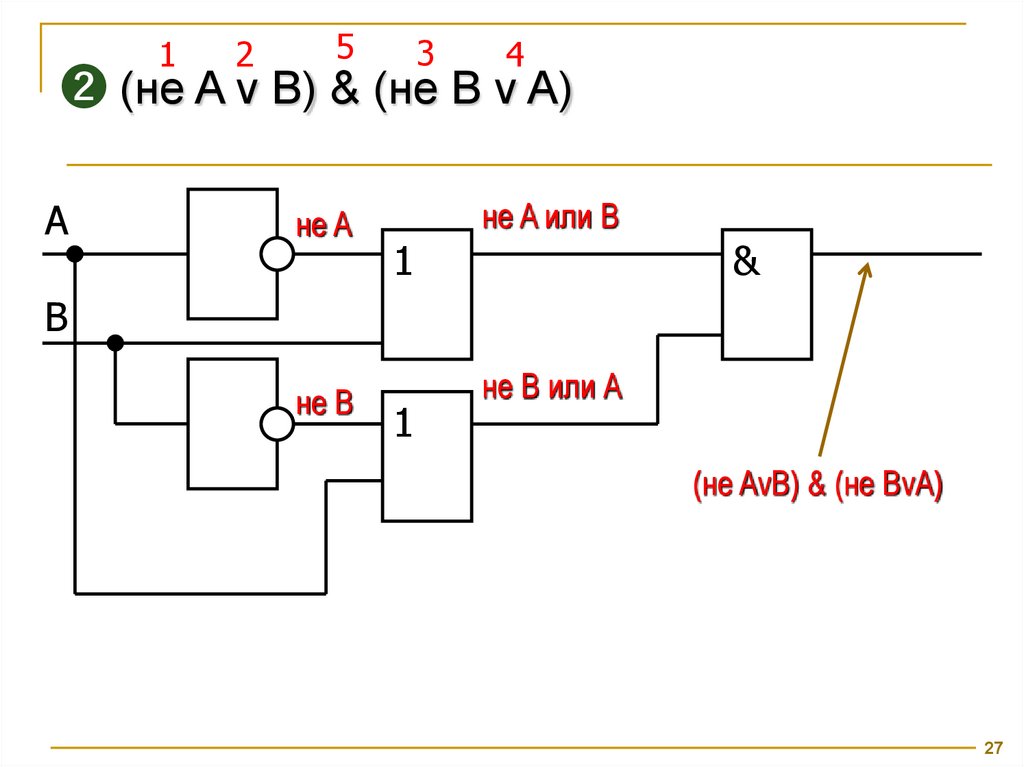
➋ (не A v B) & (не B v A)
A
не A
1
не A или B
&
B
не B
1
не В или А
(не AvB) & (не BvA)
27

28.

1
3
1
А или В
2
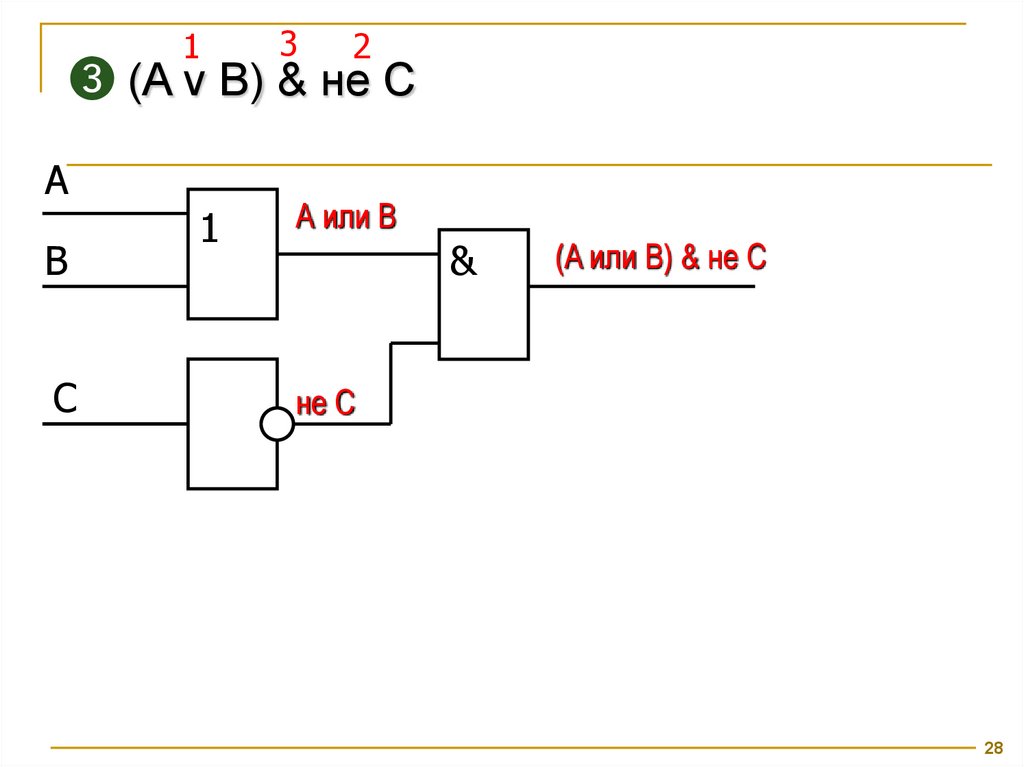
❸ (A v B) & не C
A
B
С
&
(A или B) & не C
не С
28

29.

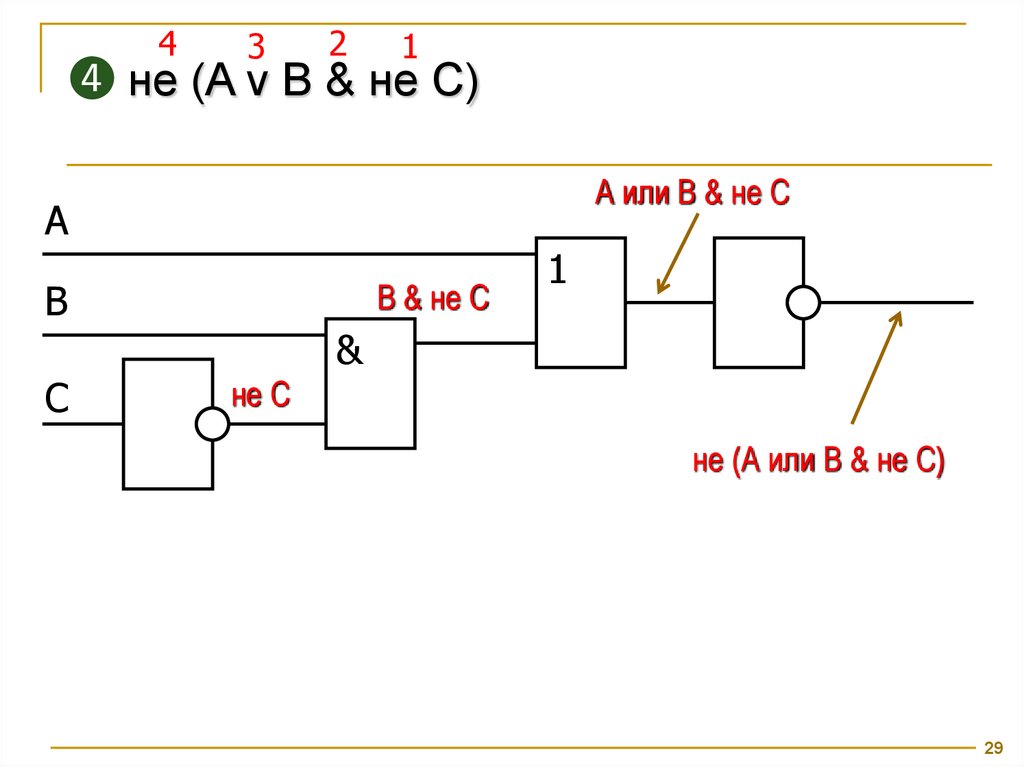
4
3
2
1
❹ не (A v B & не C)
А или В & не C
A
B
B & не C
1
&
С
не С
не (А или В & не C)
29

30.

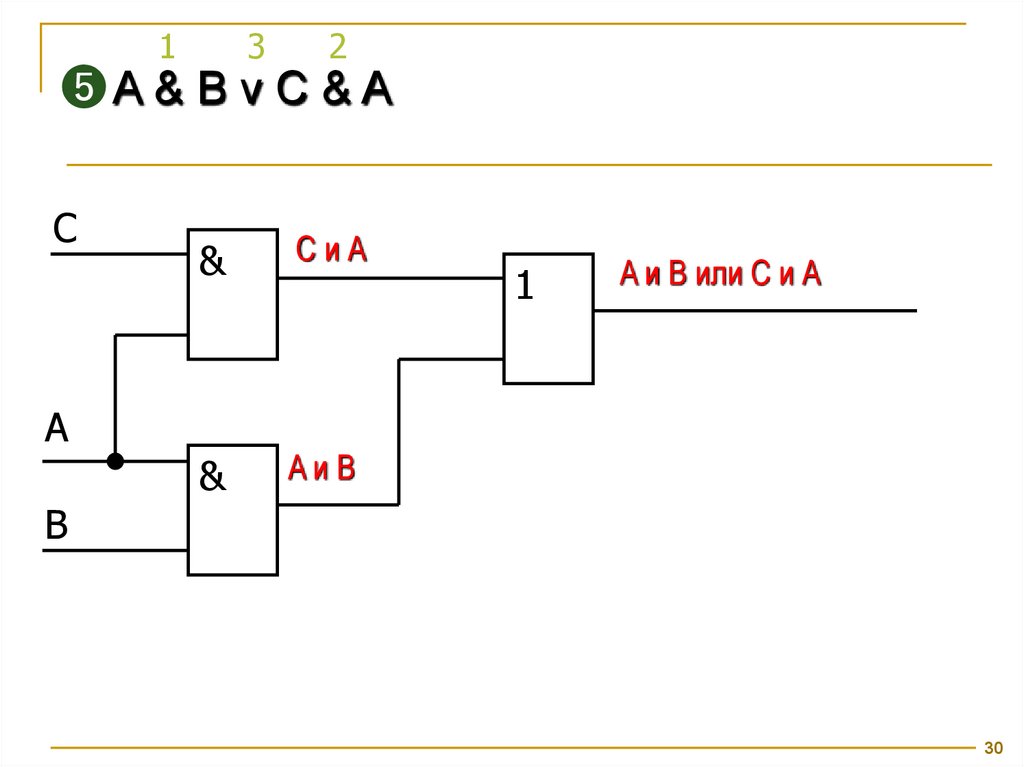
1
3
2
❺A & B v C & A
С
&
СиА
&
AиВ
A
1
A и B или С и А
B
30

31.

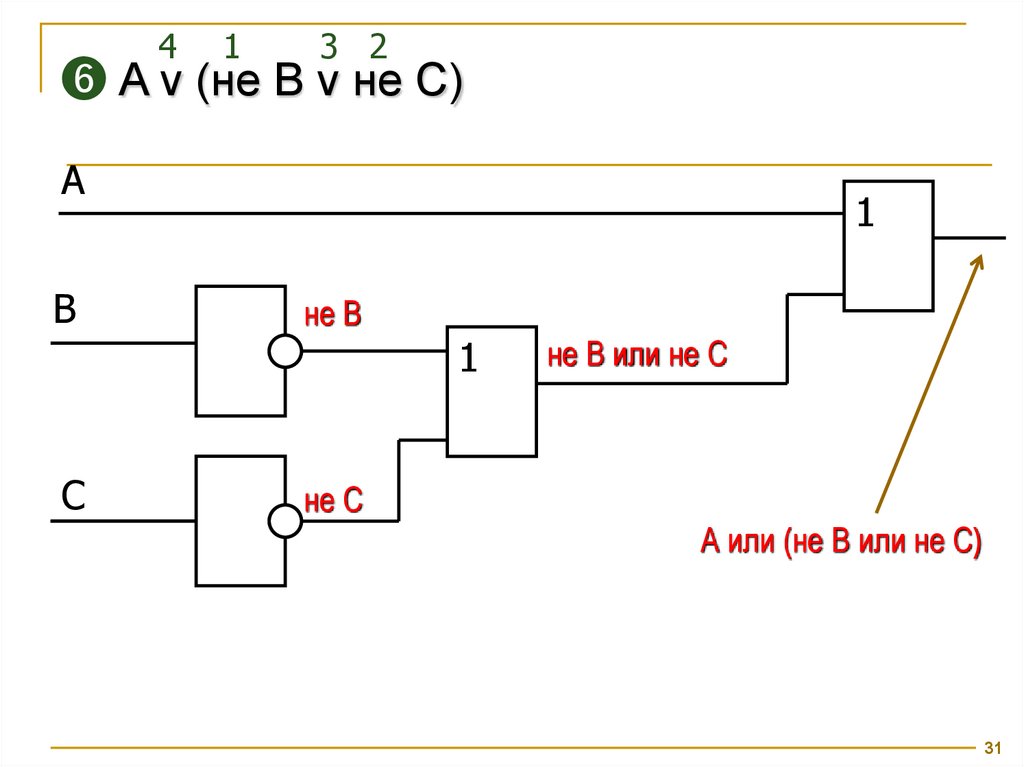
4
1
3 2
❻ A v (не B v не C)
A
B
С
1
не В
1
не B или не C
не С
А или (не B или не C)
31

32.

Построение логического
высказывания по логической схеме
1) на выходе каждого логического элемента
записать результат логической операции
2) записать получившуюся формулу на
выходе последнего элемента
32

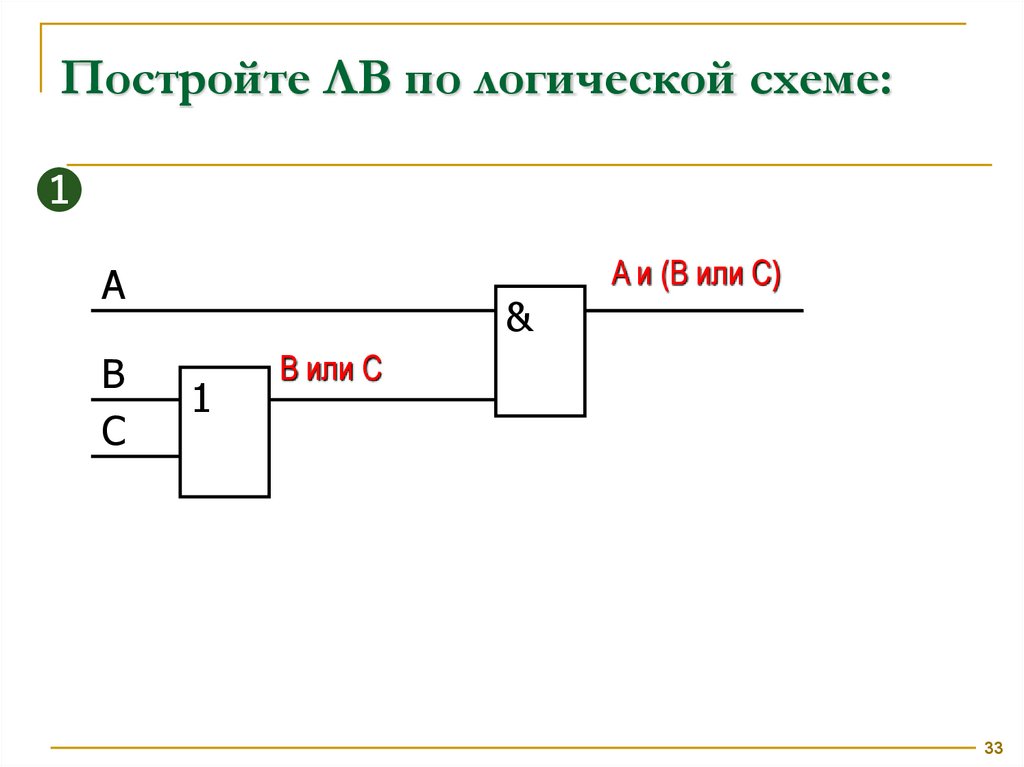
33.

Постройте ЛВ по логической схеме:
➊
A
B
C
&
1
A и (B или C)
B или C
33

34.

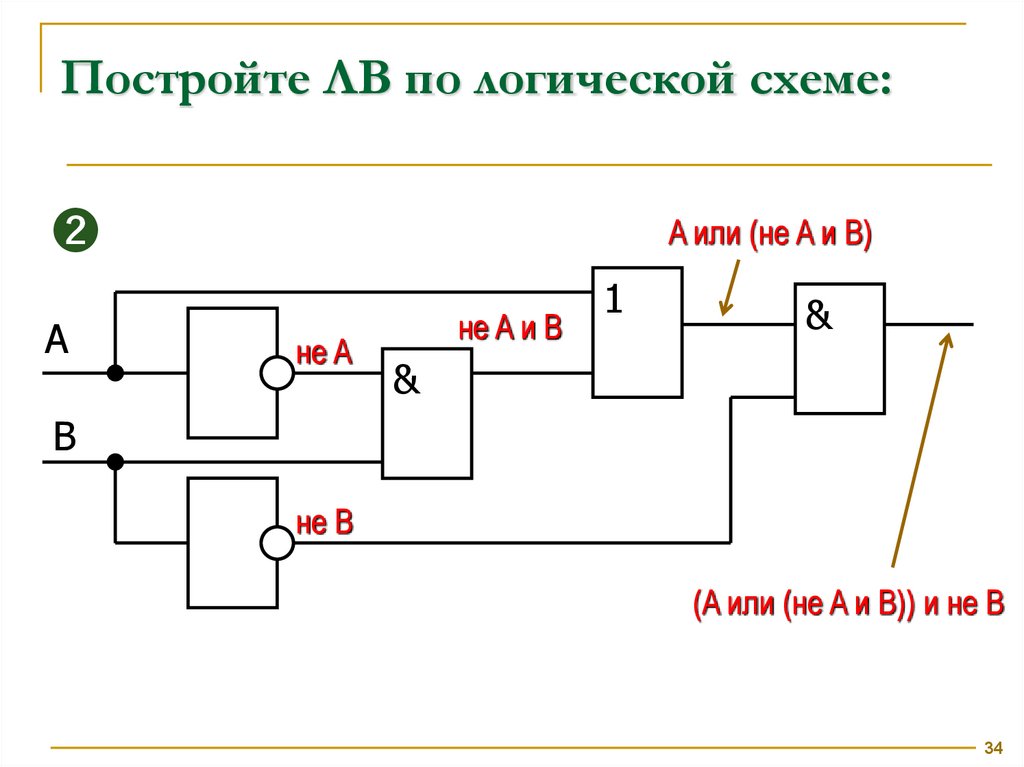
Постройте ЛВ по логической схеме:
➋
A
A или (не A и B)
не A
не A и B
1
&
&
B
не B
(A или (не A и B)) и не B
34

35.

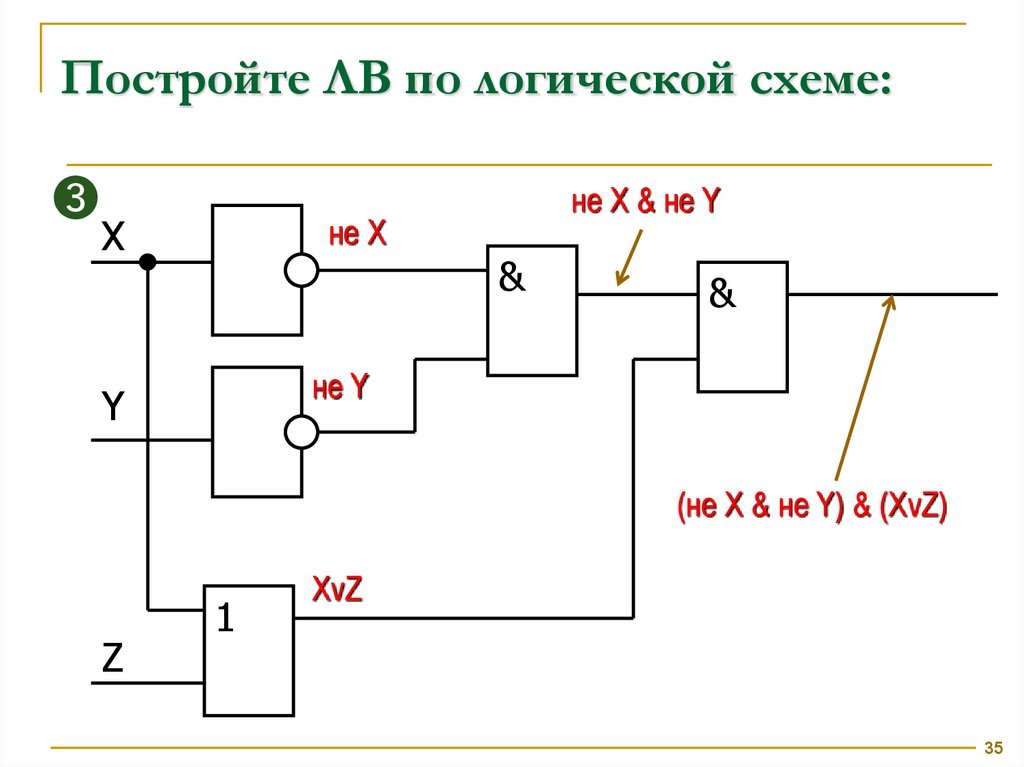
Постройте ЛВ по логической схеме:
❸
X
не X
не X & не Y
&
&
не Y
Y
(не X & не Y) & (XvZ)
Z
1
XvZ
35

36.

Постройте ЛВ по логической схеме:
❹
X
Y
Z
не X v не Y
не X
1
1
не Y
&
X & не Z
не Z
(не X v не Y) v (X & не Z)
36