Похожие презентации:
Дисперсия и стандартное отклонение случайной величины
1.
Дисперсия и стандартноеотклонение случайной
величины
11 класс
2.
ДисперсияМатематическое ожидание очень важная характеристика
случайной величины. Но часто, чтобы оценить происходящее,
математического ожидания недостаточно.
Задача 1. Один стрелок очень точно стреляет по мишени и
все попадания рядом с центром, смещение в стороны
незначительные. Второй очень плохо стреляет, и его
отметки от выстрелов разбросаны во все стороны далеко
от центра. При этом средняя не далеко от центра у обоих,
математическое ожидание у них одинаковое, но разная
кучность стрельбы.
3.
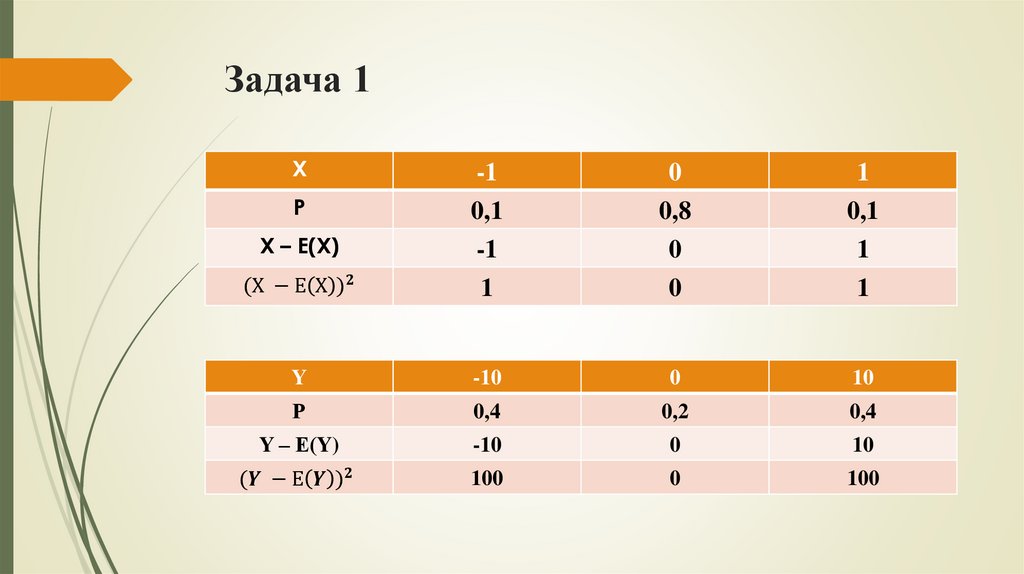
ДисперсияСтрелок X:
Х
-1
0
1
Р
0,1
0,8
0,1
Стрелок Х бьёт в цель намного чаще и промахивается недалеко:
Е(Х) = -1 · 0,1 + 0 · 0,8 + 1 · 0,1 = 0
Стрелок Y:
Y
-10
0
10
Р
0,4
0,2
0,4
Стрелок Y редко попадает в цель и промахи у него очень
далёкие от цели:
Е(Y) = -10 · 0,4 + 0 · 0,2 + 10 · 0,4 = 0
4.
ДисперсияМатематические ожидания обеих случайных величин равны
нулю. То есть у обоих стрелков прицел не смещён в сторону,
оба в среднем стреляют именно в мишень, но у них совершенно
разное рассеяние. Понятно, что у второго это рассеяние больше.
Но можно ли его вычислить для обеих случайных величин?
Насколько далеко каждый выстрел отклоняется от среднего —
от математического ожидания. Ведь что такое высокая кучность
стрельбы? Это когда все выстрелы близко друг другу.
5.
ДисперсияНа практике часто нужно знать, на сколько случайная величина отклоняется
от своего среднего значения, то есть от математического ожидания этой
случайно величины. Чтобы найти насколько одна величина отличается от
другой, находят разность между этими величинами. Но чаще не имеет
значения, в какую сторону происходит отклонение, то есть больше или
меньше случайная величина своего среднего значения, а важно узнать
именно абсолютное значение отклонения. Поэтому разность между
значением случайной величины и ее математическим ожиданием
возводят в квадрат.
Дисперсией случайной величины Х называют математическое
ожидание случайной величины (Х − Е Х )2 и обозначают
D(X):
D(X) = (Х − Е Х )


















 Математика
Математика








