Похожие презентации:
Случайная величина
1. Случайная величина.
Случайной называется величина, которая может в результатеопыта принимать то или иное числовое значение, заранее
неизвестно, какое именно.
Случайные величины обозначаются X, Y, Z, а их возможные
значения x, y, z.
Примеры.
Случайные величины бывают двух типов: дискретные и
непрерывные.
Дискретной называется случайная величина, если число ее
возможных значений конечно или счетно (т.е. их можно
пересчитать).
Дискретная случайная величина принимает отдельно
стоящие значения.
2. Случайная величина называется непрерывной, если
ее возможные значения целиком заполняют некоторыйинтервал, конечный или бесконечный.
Пример 1. Производится залп из пяти орудий. Случайная
величина X – число попаданий в цель. Ее
возможные значения : 0, 1, 2, 3, 4, 5. X – дискретная
случайная величина.
Пример 2. Испытывается машина.
Случайная величина T – время работы двигателя
от момента включения до его поломки.
Возможные значения T: 0 T . T – непрерывная
случайная величина.
3. Законом распределения (рядом распределения) дискретной случайной величины называется соответствие между ее
возможными значениями и ихX
вероятностями:
x1
x2
…
xn
P
p1
p2
…
pn
Так как события X x1 , X x 2 , ..., X x n
n
полную группу, то pi 1.
i 1
образуют
4.
Для непрерывной случайной величины закон распределениязадать нельзя, так как невозможно выписать все ее значения.
Функция распределения случайной величины.
Функцией распределения случайной величины называется
функция F (x), которая равна вероятности того, что
случайная величина X примет значение, меньшее аргумента x,
т.е.
F( x ) P(X x ).
Или
F( x ) P[X ( ; x )].
P( X ) F( ) F( )
5. Плотность распределения вероятностей непрерывной случайной величины.
Плотностью распределения вероятностейнепрерывной случайной величины называется
функция f (x) – первая производная функции
распределения F (x)
F ( x ) f ( x ) - плотность распределения
случайной величины.
6. Свойства плотности распределения.
1). Плотность распределения – неотрицательная функция: f ( x ) 0.Доказательство. Функция распределения F (x) – неубывающая
функция, поэтому ее производная f ( x ) F ( x ) - функция
неотрицательная.
x
F( x ) f ( x ) dx.
2).
Доказательство.
x
x
x
f (x ) dx F (x ) dx lim F(x ) F(x ) lim F(A) F(x ).
A
A
A
3). Вероятность попадания случайной величины в заданный интервал.
P( X ) f ( x ) dx
Доказательство.
P( X ) F( ) F( ) f ( x ) dx f ( x ) dx f ( x ) dx
7.
4).f (x ) dx 1.
Доказательство.
f ( x ) dx это вероятность того, что случайная величина
примет значение, принадлежащее интервалу ( , )
- это достоверное событие, следовательно, его вероятность равна 1.
В частности, если все возможные значения случайной величины
принадлежат интервалу (a, b), то b
f (x) dx 1.
a
8. Пример.
Дана функция распределения F (x) непрерывной случайнойвеличины X:
0, если x 0;
F( x ) ax 3 , если 0 x 1;
1, если x 1.
Найти: 1). коэффициент а,
2). плотность распределения f (x),
3). P (0,2 < X <2) – вероятность попадания случайной
величины X в интервал (0,2 ; 2).
9. Решение.
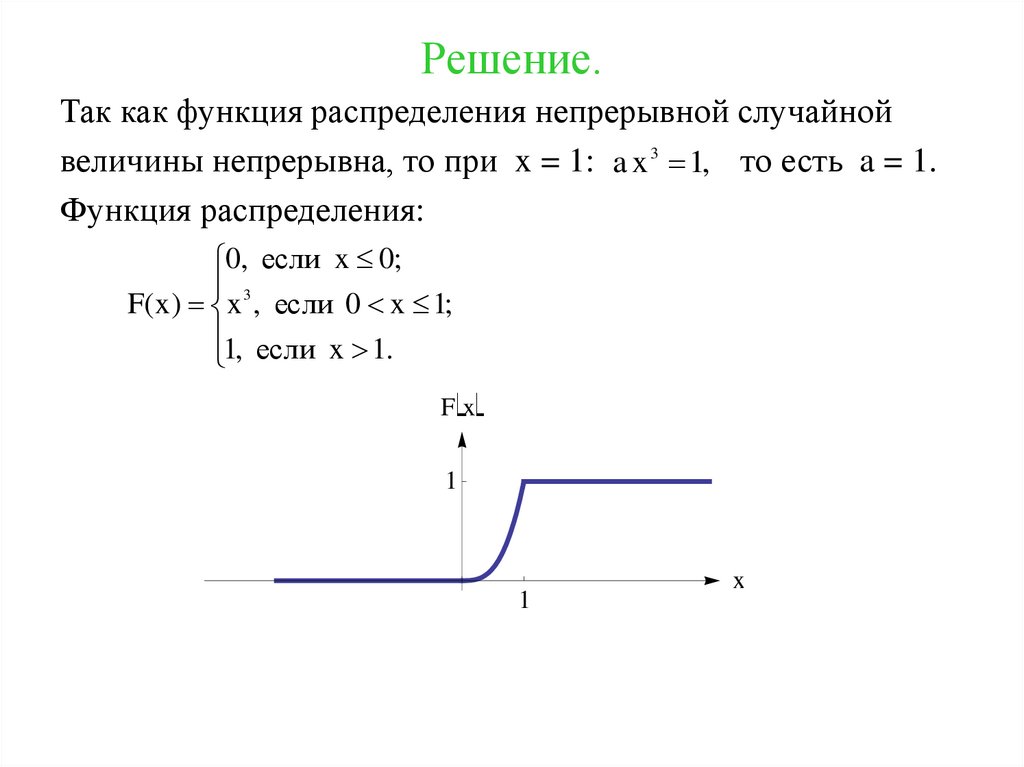
Так как функция распределения непрерывной случайнойвеличины непрерывна, то при x = 1: a x 3 1, то есть a = 1.
Функция распределения:
0, если x 0;
F( x ) x 3 , если 0 x 1;
1, если x 1.
Fx
1
1
x
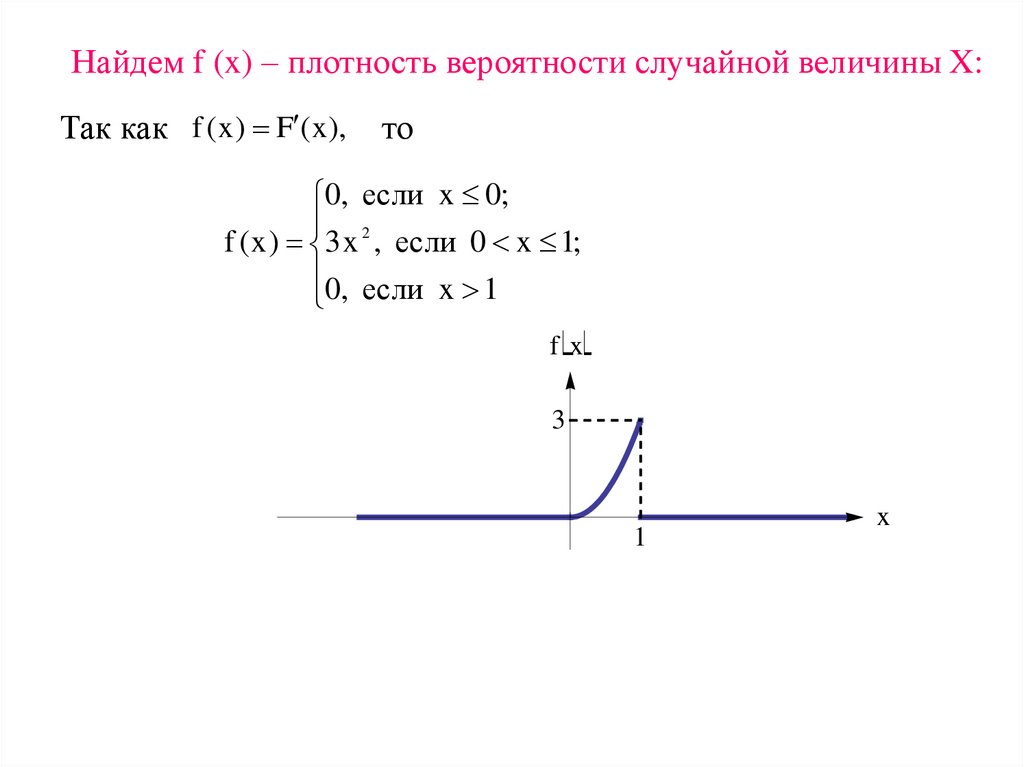
10. Найдем f (x) – плотность вероятности случайной величины X:
Так как f ( x ) F ( x ),то
0, если x 0;
f ( x ) 3 x 2 , если 0 x 1;
0, если x 1
fx
3
1
x
11. Найдем вероятность попадания случайной величины X в заданный интервал:
Применяя формулу P( X ) F( ) F( ) , получим:P (0,2 X 2) F(2) F(0,2) 1 0,23 1 0,008 0,992.
12. Числовые характеристики случайной величины.
Как известно, закон распределения полностьюхарактеризует случайную величину.
Но часто закон распределения неизвестен, и приходится
ограничиваться меньшими сведениями.
Иногда даже выгоднее пользоваться числами, которые
описывают случайную величину суммарно, такие числа
называются числовыми характеристиками случайной
величины.
К числу важных числовых характеристик относятся
математическое ожидание и дисперсия.
13. Математическое ожидание случайной величины.
Математическое ожидание приблизительно равносреднему значению случайной величины.
Если известно, что математическое ожидание числа
выбиваемых очков у первого стрелка больше, чем у второго,
то первый стрелок стреляет лучше.
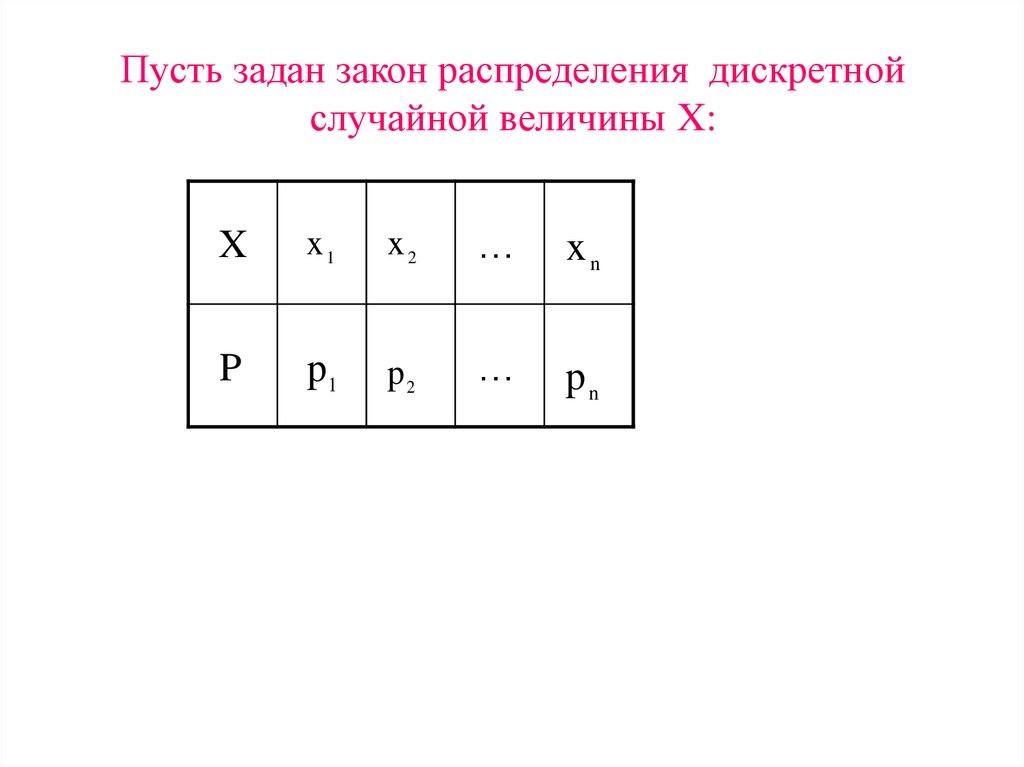
14. Пусть задан закон распределения дискретной случайной величины X:
Xx1
x2
…
xn
P
p1
p2
…
pn
15. Математическим ожиданием дискретной случайной величины X называется сумма произведений возможных значений случайной величины на
соответствующиевероятности,
то есть
n
M(X) x i pi
i 1
16. Для непрерывной случайной величины X
математическое ожидание вычисляется так:M(X) x f ( x ) dx
f (x) - плотность распределения случайной
величины X.
(Предполагается, что несобственный интеграл, сходится абсолютно, то
есть существует.)
17. Дисперсия случайной величины.
Математическое ожидание характеризует среднее значениеслучайной величины и не дает ответа на вопрос о том, как
разбросаны значения случайной величины около
математического ожидания.
Мерой разброса значений случайной величины
относительно математического ожидания служит
дисперсия.
18. Отклонением случайной величины X от ее математического ожидания M (X) = a называется случайная величина, равная разности X – a.
Дисперсией случайной величины X называетсяматематическое ожидание квадрата отклонения
случайной величины X от ее математического
ожидания.
D(X) M [(X a )]
2
19.
Для дискретной случайной величины:n
D(X) M [(X a )] pi ( x i a ) .
2
2
i 1
Для непрерывной случайной величины:
D(X) M [(X a )] ( x a ) f ( x ) dx.
2
2
20.
(X) D(X) - среднее квадратическое отклонение.Для вычисления дисперсии удобна следующая формула:
D( X ) M ( X ) [ M ( X ) ]
2
2
Дисперсия равна математическому ожиданию квадрата
случайной величины минус квадрат ее математического
ожидания.
21.
D( X ) M ( X ) [ M ( X ) ]2
2
Докажем эту формулу.
Пусть M (X) = а.
D(X) M [(X a )]2 M [X 2 2a X a 2 ]
M ( X 2 ) 2 M (a X ) M (a 2 )
M (X 2 ) 2M (a ) M (X) M (a 2 ) M (X 2 ) 2a a a 2
M (X 2 ) a 2 M (X 2 ) [ M (X)]2 .
22. ПРИМЕР.
Известен закон распределения дискретной случайнойвеличины X:
X
2
3
5
P
0,1 0,6 0,3
Математическое ожидание:
n
M(X) x i pi 2 0,1 3 0,6 5 0,3 3,5.
i 1
23. Найдем дисперсию по формуле:
D(X) M (X 2 ) [ M (X)]2Для этого определим M ( X 2 ) :
X2
4
9
25
P
0,1
0,6
0,3
n
M(X ) x i2 pi 4 0,1 9 0,6 25 0,3 13,3.
2
i 1
Тогда дисперсия равна:
D(X) M (X 2 ) [ M (X)]2 13,3 3,52 1,05.
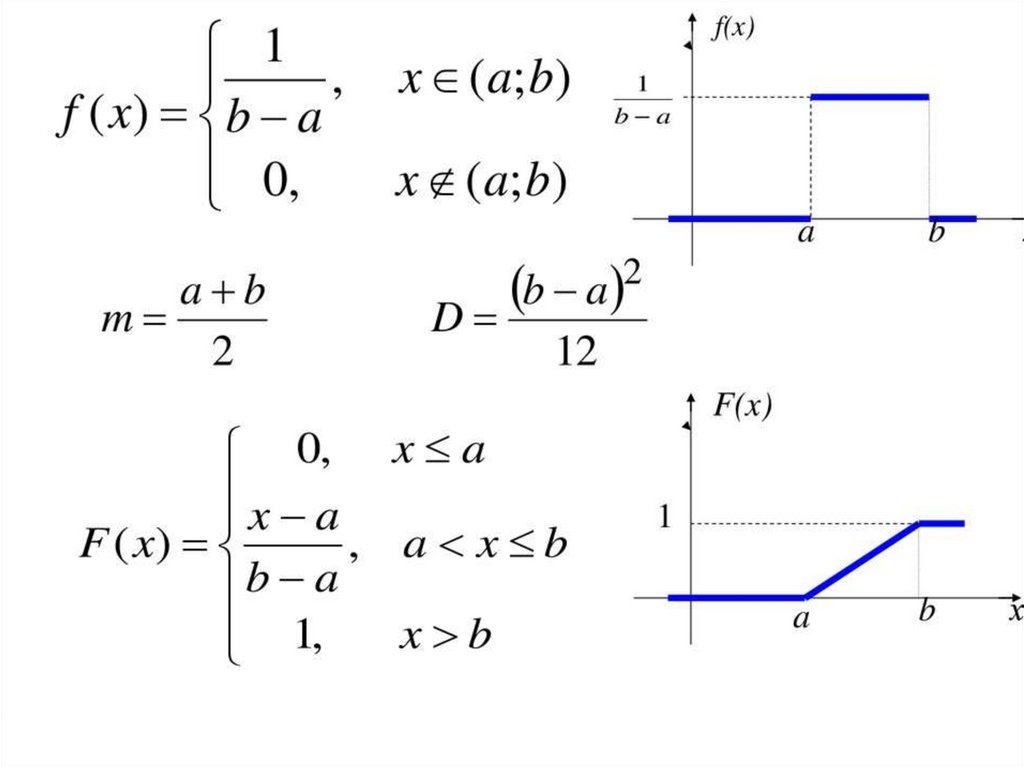
24. Равномерное распределение
Дана плотность распределения0, x a
f ( x ) C, a x b
0, x b
a
b
a
b
f ( x )dx 1
f ( x )dx 0dx Cdx 0dx 1 C
0, x a
1
f(x)
,a x b
b
a
0, x b
1
b a
25. Функция распределения
xПо определению
F( x ) f ( x )dx . В нашем случае
1. x<a
x
F( x ) 0dx 0
2.
a x b
3. x>b
x
a
1
x a
dx
b a
b a
a
x
F( x ) f ( x )dx 0dx
x
a
b
x
1
F( x ) f ( x )dx 0dx
dx 0dx 1
b a
a
b
0, x a
x a
F( x )
,a x b
b a
1, x b

















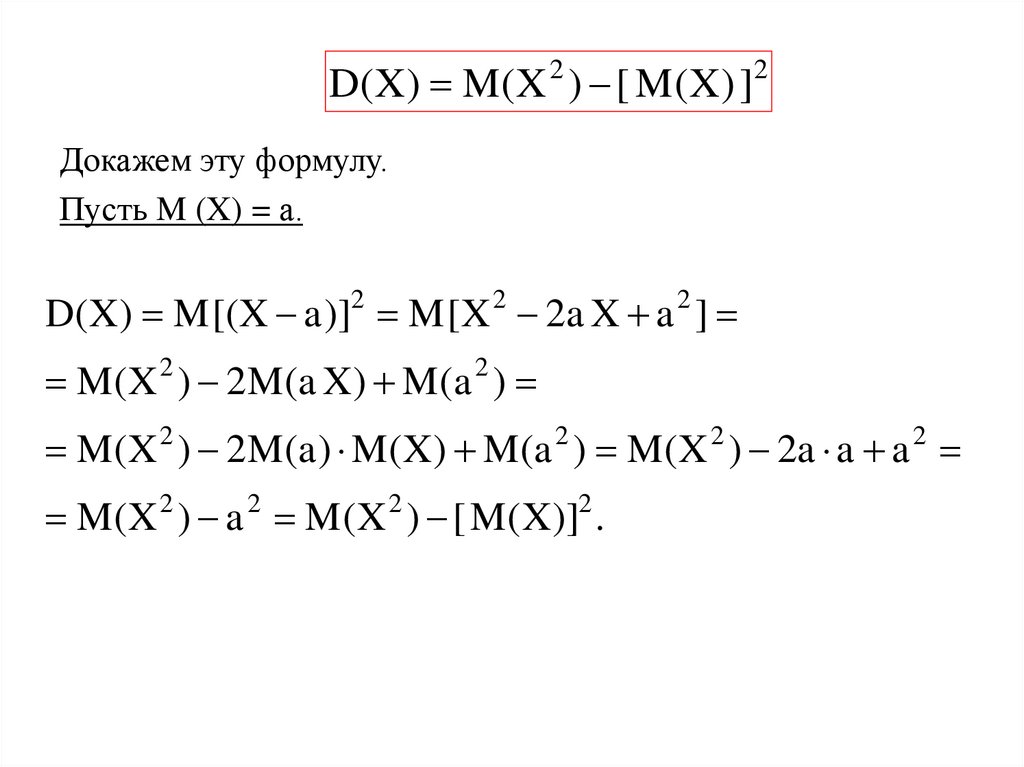




 Математика
Математика








