Похожие презентации:
Исследование палиндромных чисел
1.
Исследование палиндромныхчисел
Исследовательский
2.
ЦельИсследовать свойства палиндромных чисел и разработать алгоритм их генерации.
2
3.
Задачи1. Определить и описать свойства палиндромных чисел. 2. Рассмотреть примеры и показать, как
легко можно генерировать новые палиндромные числа. 3. Разработать алгоритм для поиска
палиндромных чисел в заданном диапазоне. 4. Подготовить отчет о результатах исследования.
3
4.
ПроблемаНедостаточная осведомленность о палиндромных числах и их практическом применении.
4
5.
Введение в палиндромные числаПалиндромные числа – это уникальные объекты математики, читающиеся одинаково с обеих
сторон. Они вызывают интерес как у математиков, так и у программистов, исследуя симметрию и
гармонию чисел. В данной работе мы стремимся понять свойства палиндромных чисел, методы их
генерации и алгоритмы поиска. Актуальность исследования связана с недостаточной
осведомленностью о применении палиндромных чисел в криптографии, компьютерной графике и
других сферах. Мы также обсудим существующую литературу и выявим направления для будущих
исследований.
5
6.
Введение в палиндромные числаПалиндромные числа представляют собой уникальный класс чисел, которые читаются одинаково
слева направо и справа налево, например, 16461. Они находят применение в теории чисел и
программной инженерии, а также обнаруживаются в различных системах счисления. Примеры
палиндромов, такие как 8 и 676, демонстрируют наличие симметрии, что делает их удобными для
математических операций. Бесконечно много палиндромов существует, благодаря возможности
модификации их цифр. Эти числа привлекают внимание ученых благодаря своей универсальности и
полезности в алгоритмах обработки данных.
6
7.
Свойства палиндромных чиселПалиндромные числа обладают уникальными свойствами, делающими их интересными для
исследований. Первое – это симметрия: однозначные числа всегда палиндромы, а в многозначных
цифры, находящиеся на симметричных позициях, совпадают. Второе свойство заключается в
структуре, где палиндромы могут возникать из перестановок своих цифр. Имеется множество
методов генерации палиндромов, включая операции с квадратами чисел. Важным фактом является
также их бесконечное множество и наличие гипотез о закономерностях между палиндромами и
другими числовыми категориями.
7
8.
Генерация палиндромных чиселГенерация палиндромных чисел включает несколько методов, таких как непосредственное
формирование чисел, проверка и создание определенного количества палиндромов. Первый
метод позволяет создавать палиндром, соединяя число с его реверсией. Второй метод проверяет,
является ли число палиндромом, сравнивая его с реверсированной строкой. Также существуют
алгоритмы для нахождения ближайших палиндромов, что полезно в различных задачах.
Учитывание различных систем счисления расширяет возможности генерации, позволяя
исследовать свойства чисел более глубоко.
8
9.
Алгоритмы поиска палиндромных чиселАлгоритмы поиска палиндромных чисел, в частности алгоритм Манакера, играют важную роль в
алгоритмике. Он позволяет находить все палиндромы в строке за линейное время, значительно
превосходя наивные методы по производительности. Алгоритм разделяет палиндромы на четные и
нечетные, оптимизируя поиск через актуализацию границ. Генерация массива с длиной
максимального палиндрома для каждого индекса снижает количество проверок. Альтернативные
методы, такие как динамическое программирование, менее эффективны, что делает алгоритм
Манакера предпочтительным для решения задач.
9
10.
Схемы алгоритмов для поиска палиндромныхчисел
10
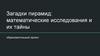
11.
Схемы алгоритмов для поиска палиндромныхчисел
11
12.
Примеры практического примененияпалиндромных чисел
Палиндромные числа имеют широкий спектр применения. В математике они становятся объектом
увлекательных задач, таких как поиск палиндромных простых чисел и череда чисел, которые при
сложении со своими обратными значениями формируют палиндром. В информатике они
применяются для анализа текстов и поиска паттернов. Алгоритмы, основанные на палиндромах,
актуальны в обработке естественного языка. Кроме того, палиндромы обогащают литературу,
становясь основой для словесных игр и стихов, что подчеркивает их креативное и культурное
значение.
12
13.
Примеры использования палиндромных чиселв математике и их применение в алгоритмах
13
14.
Примеры использования палиндромных чиселв математике и их применение в алгоритмах
14
15.
Обзор литературы по теме палиндромных чиселПалиндромные числа занимают важное место в теории чисел, исследуются в различных системах
счисления. Работы В.В. Любимова и Р.В. Меликджаняна анализируют количество палиндромов в
зависимости от разрядов. Исследуются числа, возникающие при делении на девять, которые
демонстрируют интересные палиндромные структуры. Гипотеза Лишрел о непалиндромизируемых
числах привлекает внимание математиков, открывая новые свойства чисел. Практическое
применение палиндромов в информатике и криптографии подчеркивает их значимость для
создания алгоритмов.
15
16.
Заключение: Значение исследованияПалиндромные числа представляют собой уникальную область в математике, сочетая симметрию и
разнообразные свойства. Их изучение углубляет понимание чисел и открывает новые
математические концепции. Применение палиндромов в таких областях, как анализ данных и
программирование, подтверждает их важность. Исследования также провоцируют интересные
гипотезы о числах, создавая возможности для дальнейших исследований. Палиндромы служат
мостом между теорией и практикой, обогащая нашу математику и создавая новые горизонты для
будущих ученых.
16
17.
Примеры и методы преобразования чисел впалиндромы
17
18.
Примеры и методы преобразования чисел впалиндромы
18
19.
ЗаключениеВ ходе нашего исследования палиндромных чисел мы углубили понимание их свойств и
практического применения. Эти числа, читающиеся одинаково с обеих сторон, имеют значительное
значение в математике, симметрии и структуре. Мы разработали эффективные алгоритмы для
генерации палиндромов, которые могут найти применение в криптографии и анализе данных. Наше
исследование подчеркивает, что палиндромные числа не только абстрактная концепция, но и
мощный инструмент для решения задач в науке и технике.
19
20.
Список литературы1. Палиндромное число - Palindromic number - Википедия. Доступно:
https://en.wikipedia.org/wiki/palindromic_number
2. Числа-палиндромы — Википедия. Доступно: https://ru.wikipedia.org/wiki/числа-палиндромы
3. Палиндромы среди простых чисел | Наука... Доступно: https://www.nkj.ru/archive/articles/17984/
4. Магия математики: числа-палиндромы. Доступно: https://dzen.ru/a/xosifl79ojj5e0ps
5. Научно-практическая работа по математике на тему: Палиндромы. Доступно:
https://infourok.ru/nauchnoprakticheskaya-rabota-po-matematike-na-temu-palindromi-v-matematike-klassi3072309.html
6. Палиндромы в математике | nsportal.ru. Доступно: https://nsportal.ru/ap/library/nauchnotekhnicheskoe-tvorchestvo/2017/01/13/palindromy-v-matematike
20



















 Математика
Математика