Основные положения сопротивления материалов

1.

2.

Основоположником этой науки считают итальянского ученого Г. Галилея
(1564-1642 гг.)

3.

ВВЕДЕНИЕ
Сопротивление материалов - это раздел
механики, в котором рассматриваются
твердые деформируемые тела.
Основной
задачей
СМ
является
разработка инженерных методов расчета
элементов конструкций
на
прочность,
жесткость и устойчивость.
3

4.

Сопротивлен
ие
материалов
Теоретическая
часть
Экспериментальная
часть
Теоретическая
механика
Физика
Математика
Материаловедение
4

5.

6.

7.

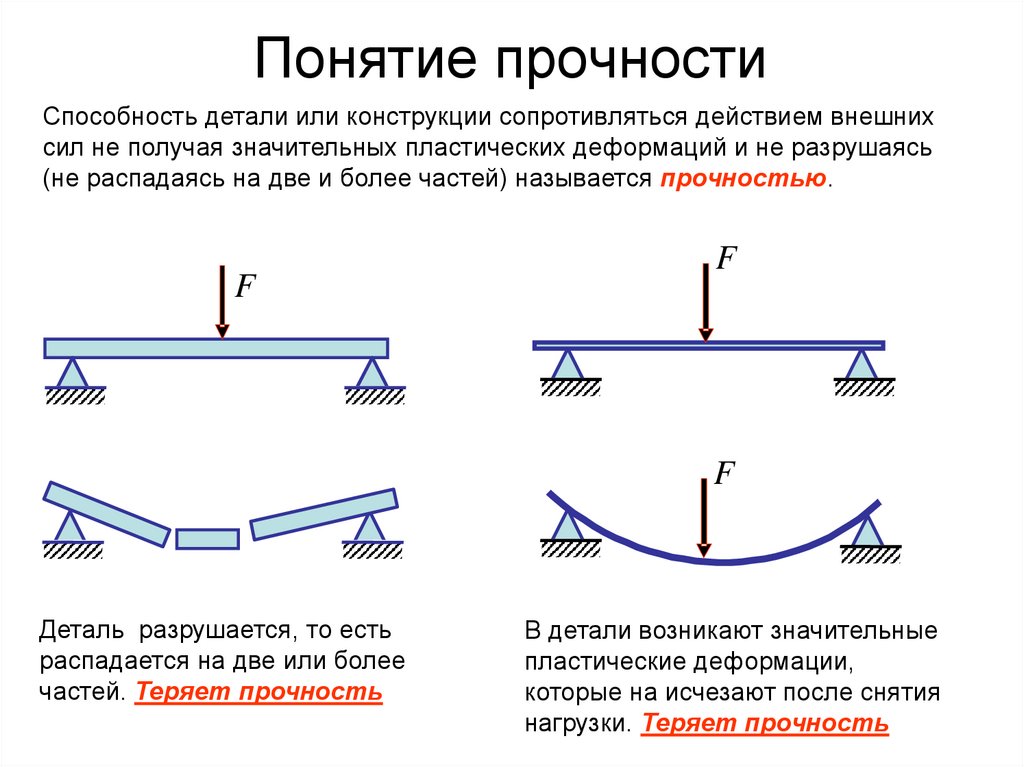
Понятие прочности
Способность детали или конструкции сопротивляться действием внешних
сил не получая значительных пластических деформаций и не разрушаясь
(не распадаясь на две и более частей) называется прочностью.
F
F
F
Деталь разрушается, то есть
распадается на две или более
частей. Теряет прочность
В детали возникают значительные
пластические деформации,
которые на исчезают после снятия
нагрузки. Теряет прочность

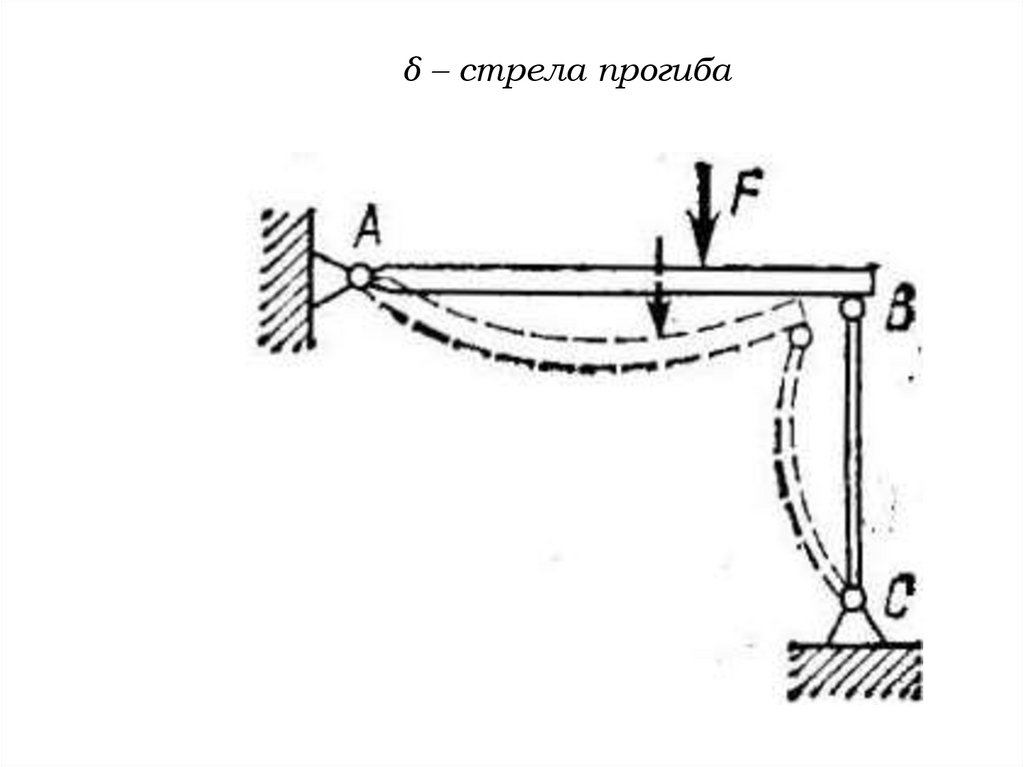
8.

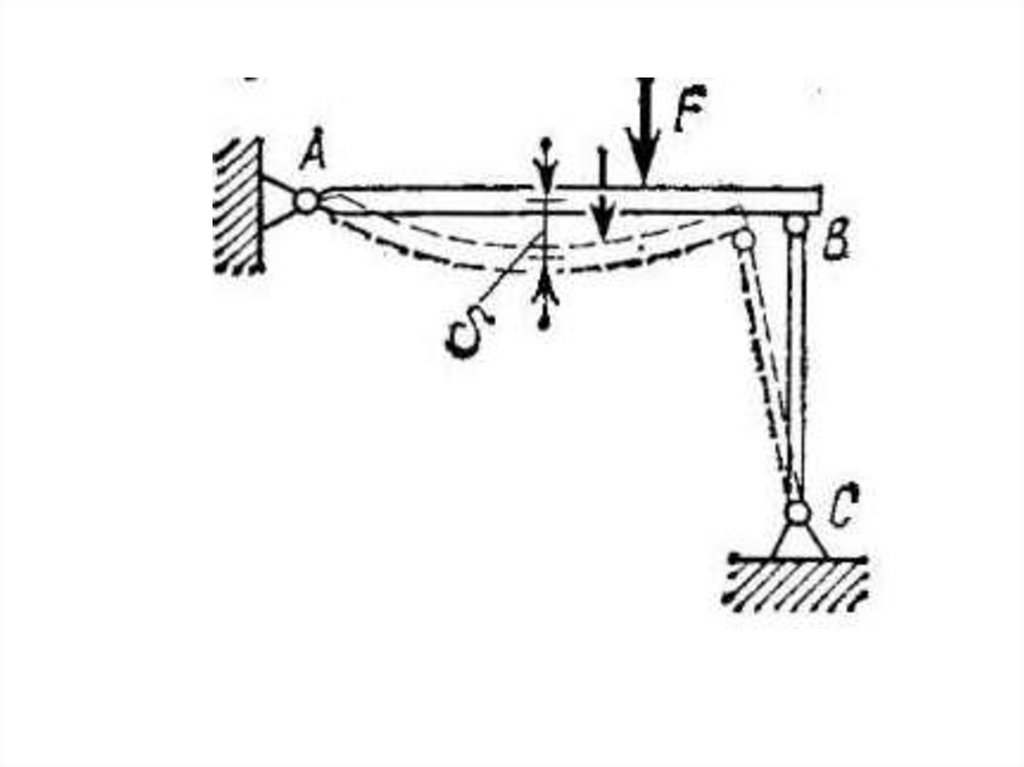
δ – стрела прогиба

9.

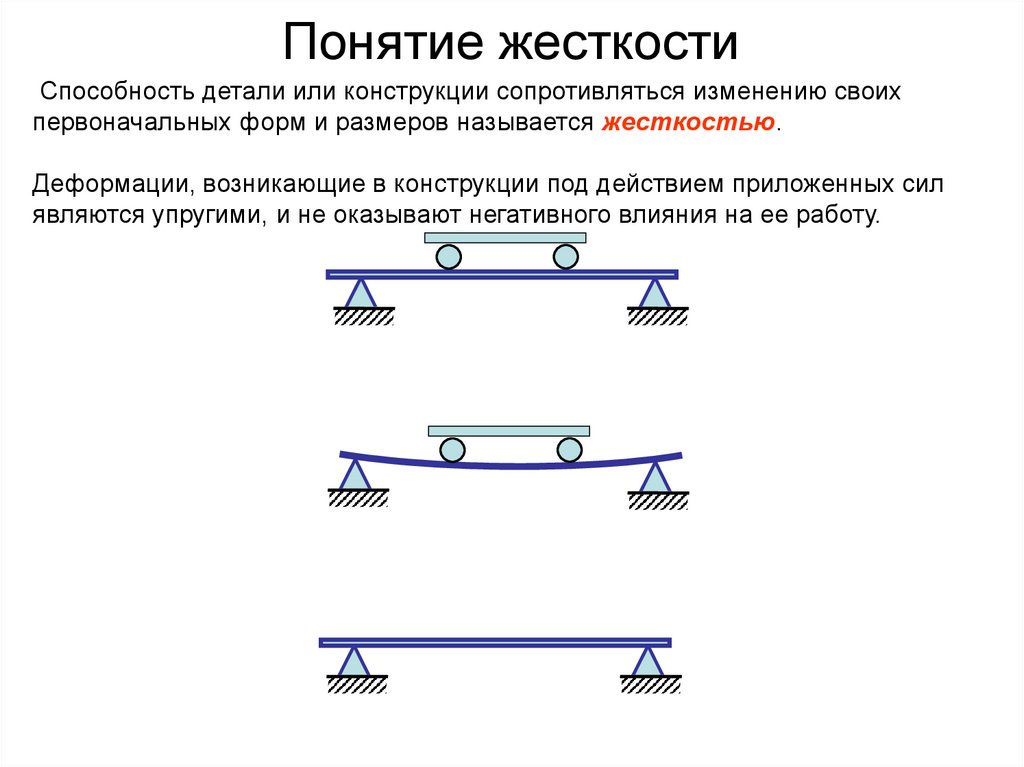
Понятие жесткости
Способность детали или конструкции сопротивляться изменению своих
первоначальных форм и размеров называется жесткостью.
Деформации, возникающие в конструкции под действием приложенных сил
являются упругими, и не оказывают негативного влияния на ее работу.

10.

Понятие устойчивости Не устойчива
Конструкция или деталь называется устойчивой,
если в результате действия на нее заданных
нагрузок она сохраняет первоначальную форму
упругого равновесия.
F
F
Не устойчива
F
Устойчива
Устойчива

11.

• Усталость – процесс постепенного
накопления повреждений под действием
переменных напряжений, приводящий к
изменению свойств, образованию трещин, их
развитию и разрушению.
• Надежность – свойство объекта сохранять
работоспособное состояние в течение
некоторого времени или некоторой
наработки.
• Долговечность – свойство элемента или
системы длительно сохранять
работоспособность до наступления
предельного состояния при определенных
условиях эксплуатации.

12.

Задача сопротивления материалов:
определение деформаций и
напряжений в твердом упругом теле,
которое подвергается силовому или
тепловому воздействию.

13.

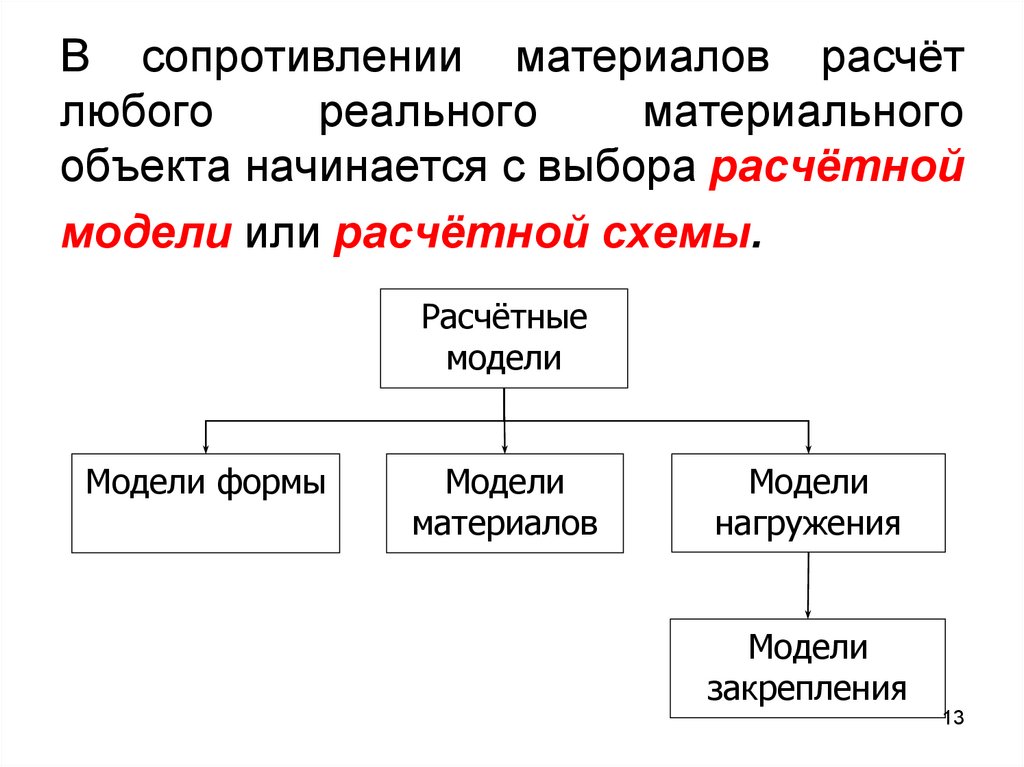
В сопротивлении материалов расчёт
любого
реального
материального
объекта начинается с выбора расчётной
модели или расчётной схемы.
Расчётные
модели
Модели формы
Модели
материалов
Модели
нагружения
Модели
закрепления
13

14.

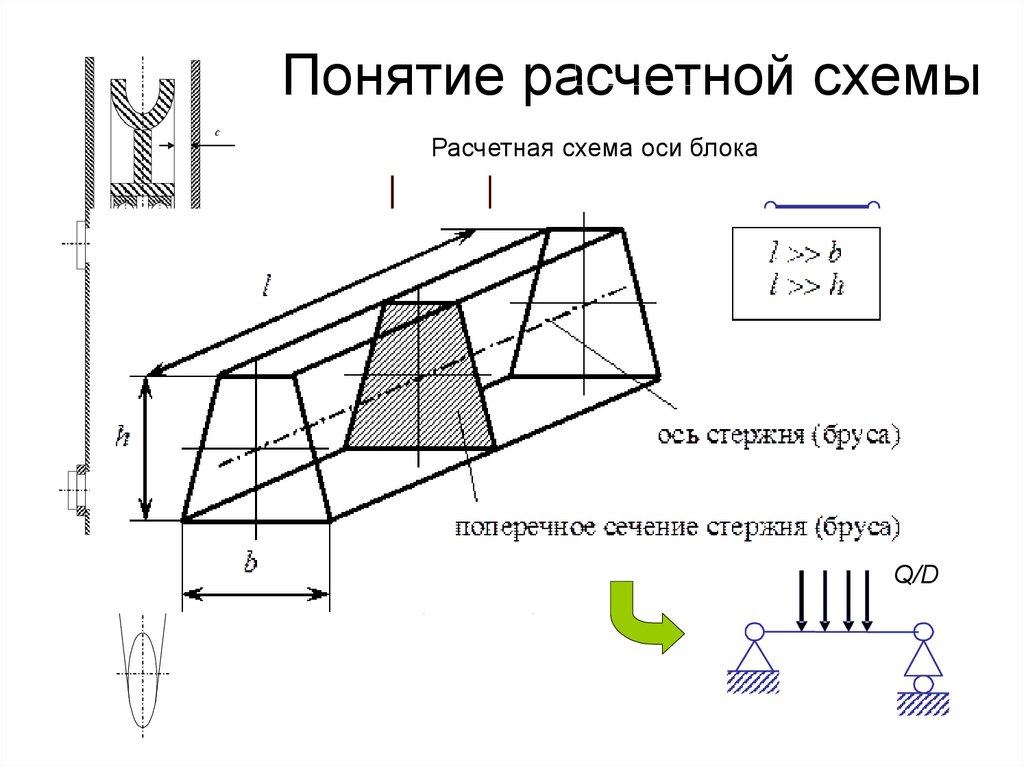
Понятие расчетной схемы
Условное изображение конструкции или детали принимаемое для выполнения
расчета, называется расчетной схемой.
Расчетная схема выбирается так, чтобы существенно упростить расчет, не
искажая действительной картины работы конструкции или детали
Расчетную схему составляют в следующем порядке:
1. Разбивают конструкцию на простые элементы
2. Каждый простой элемент конструкции заменяют соответствующим
расчетным элементом (брусом, пластиной, оболочкой, массивным телом);
3. Выбирают схему опорных частей элемента или конструкции (подвижный и
неподвижный шарнир, жесткая заделка и другие);
4. Выбирают вариант соединения элементов конструкции между собой и с
опорными частями (жесткий или шарнирный) .

15.

16.

Понятие расчетной схемы
с
Расчетная схема оси блока
Q/2
Q/2
Расчетная схема траверсы крюка
Q
Q/D

17.

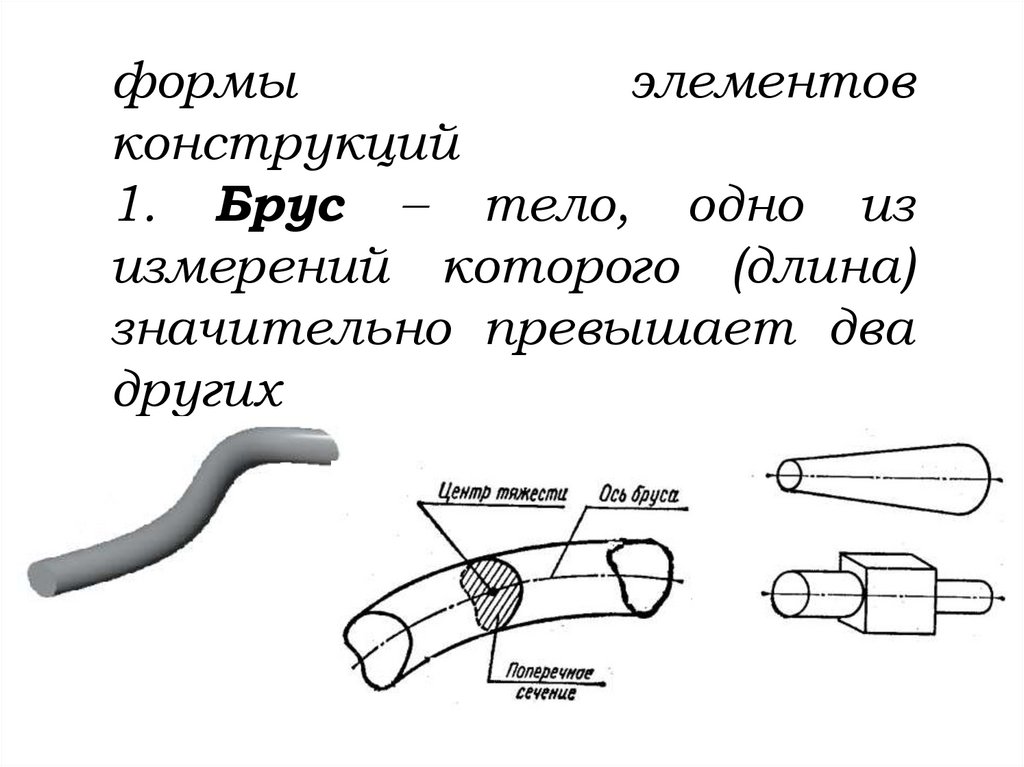
формы
элементов
конструкций
1. Брус – тело, одно из
измерений которого (длина)
значительно превышает два
других

18.

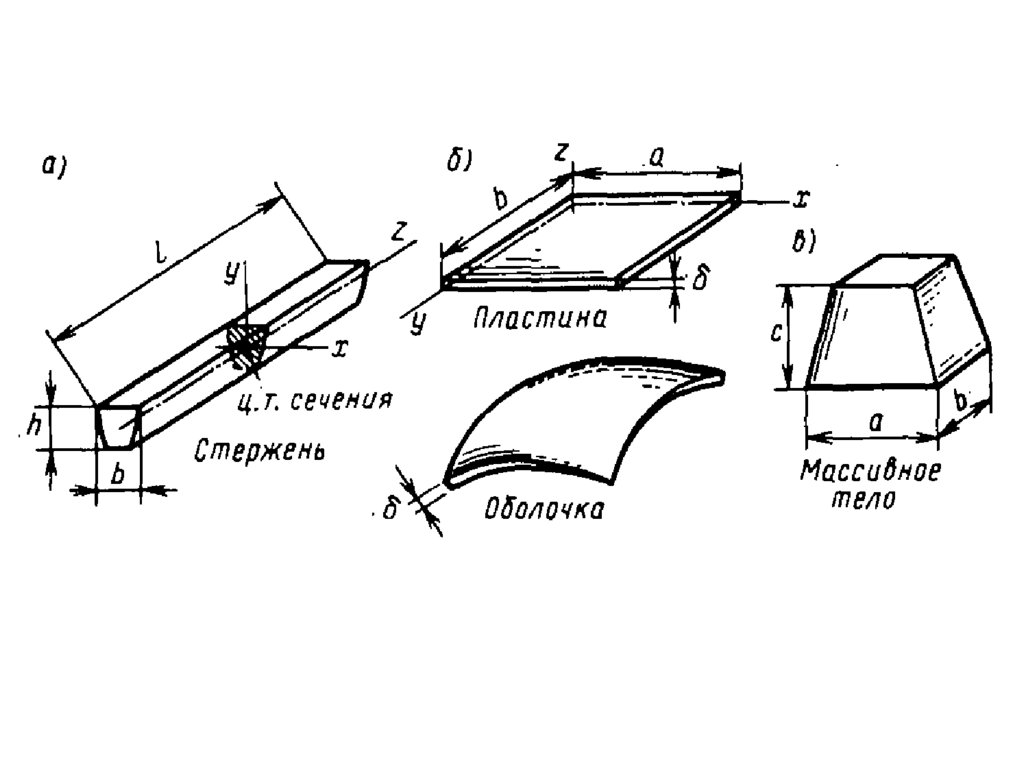
Расчетные формы и их
классификация
По форме поперечного сечения
постоянного сечения и переменного
сечения.
По форме оси – прямолинейные и
криволинейные брусья.

19.

2. Оболочка – тело, одно из
измерений которых (толщина) во
много раз меньше двух других
размеров.
Серединная поверхность

20.

Расчетные формы и их классификация
Оболочки могут иметь цилиндрическую,
коническую или сферическую форму.
Оболочка, срединная поверхность которой
представляет собой плоскость, называется
пластинкой.
Встречаются пластинки прямоугольные и круглые.

21.

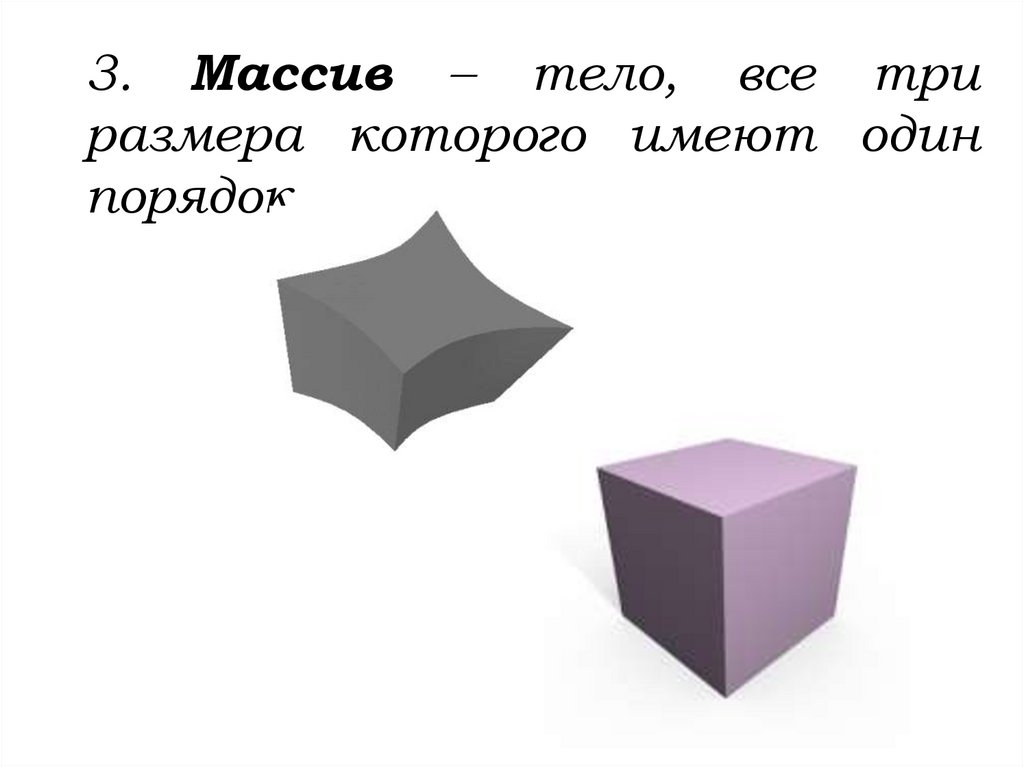
3. Массив – тело, все три
размера которого имеют один
порядок

22.

23.

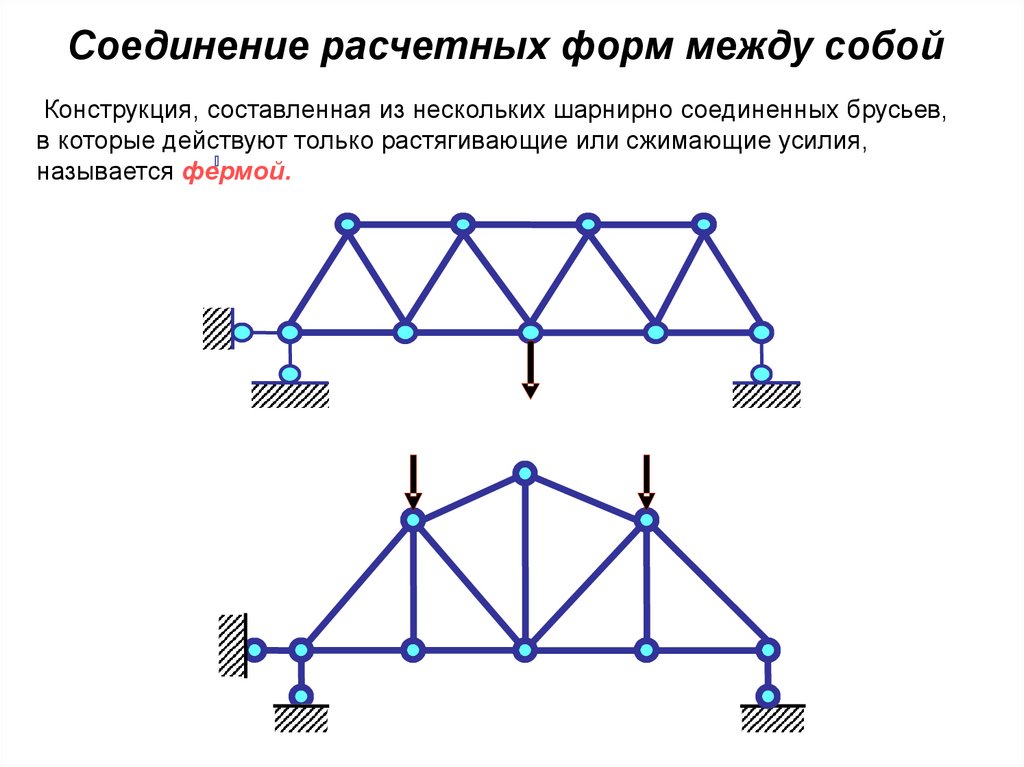
Соединение расчетных форм между собой
Конструкция, составленная из нескольких шарнирно соединенных брусьев,
в которые действуют только растягивающие или сжимающие усилия,
называется фермой.

24.

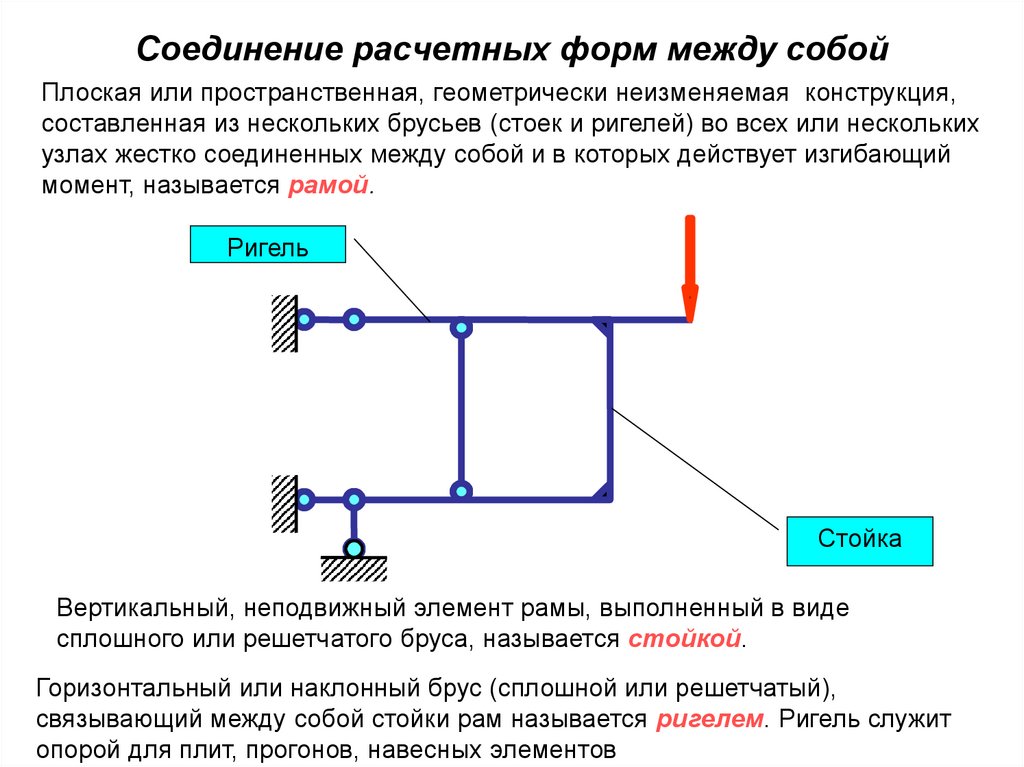
Соединение расчетных форм между собой
Плоская или пространственная, геометрически неизменяемая конструкция,
составленная из нескольких брусьев (стоек и ригелей) во всех или нескольких
узлах жестко соединенных между собой и в которых действует изгибающий
момент, называется рамой.
Ригель
Стойка
Вертикальный, неподвижный элемент рамы, выполненный в виде
сплошного или решетчатого бруса, называется стойкой.
Горизонтальный или наклонный брус (сплошной или решетчатый),
связывающий между собой стойки рам называется ригелем. Ригель служит
опорой для плит, прогонов, навесных элементов

25.

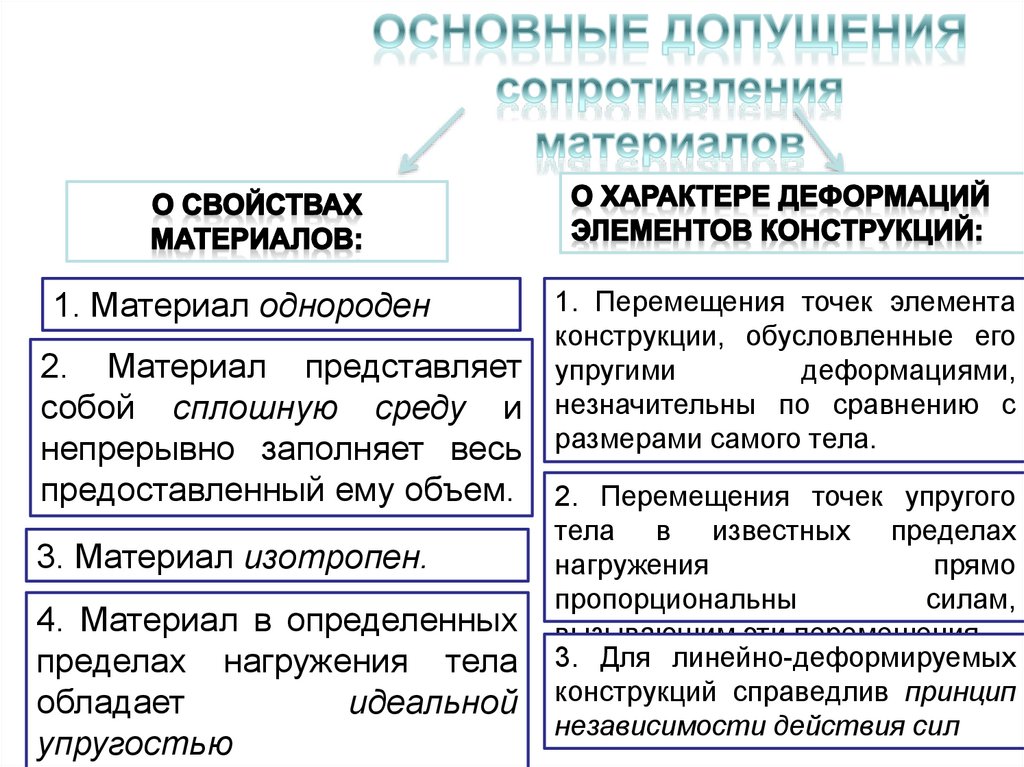
1. Материал однороден
1. Перемещения точек элемента
конструкции, обусловленные его
упругими
деформациями,
незначительны по сравнению с
размерами самого тела.
2. Материал представляет
собой сплошную среду и
непрерывно заполняет весь
предоставленный ему объем. 2. Перемещения точек упругого
3. Материал изотропен.
4. Материал в определенных
пределах нагружения тела
обладает
идеальной
упругостью
тела в известных пределах
нагружения
прямо
пропорциональны
силам,
вызывающим эти перемещения.
3. Для линейно-деформируемых
конструкций справедлив принцип
независимости действия сил

26.

Допущения и гипотезы
в сопротивлении материалов
1. Допущения о свойствах
материалов: (модели материалов)
материал считается:
• сплошным;
• однородным;
• изотропным;
• идеально-упругим.
26

27.

• Сплошность – понятие, предполагающее,
что материал полностью заполняет
занимаемый объем и распределен в нем без
пустот и разрывов.
• Однородность –свойства материала во
всех точках тела одинаковы.
• Изотропность - свойства материала во
всех направлениях одинаковы.
Пример: сталь изотропна, дерево анизотропно.
• Идеальная упругость – свойство
полностью восстанавливать форму и
размеры после устранения причин,
вызвавших эти изменения.
27

28.

2. Допущения о деформациях:
• Упругие (обратимые) деформации –
исчезают после устранения причин,
их вызвавших (например, после
снятия нагрузки);
• Пластические (необратимые)
деформации – остаются после
устранения причин, их вызвавших
(например, после снятия нагрузки).
28

29.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
1. Гипотеза сплошности и
однородности —
материал представляет собой
однородную сплошную среду;
2. Гипотеза об изотропности
материала –
физико-механические свойства
материала одинаковы по всем
направлениям.
3.Гипотеза об идеальной упругости
материала – тело способно
восстанавливать свою первоначальную

30.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
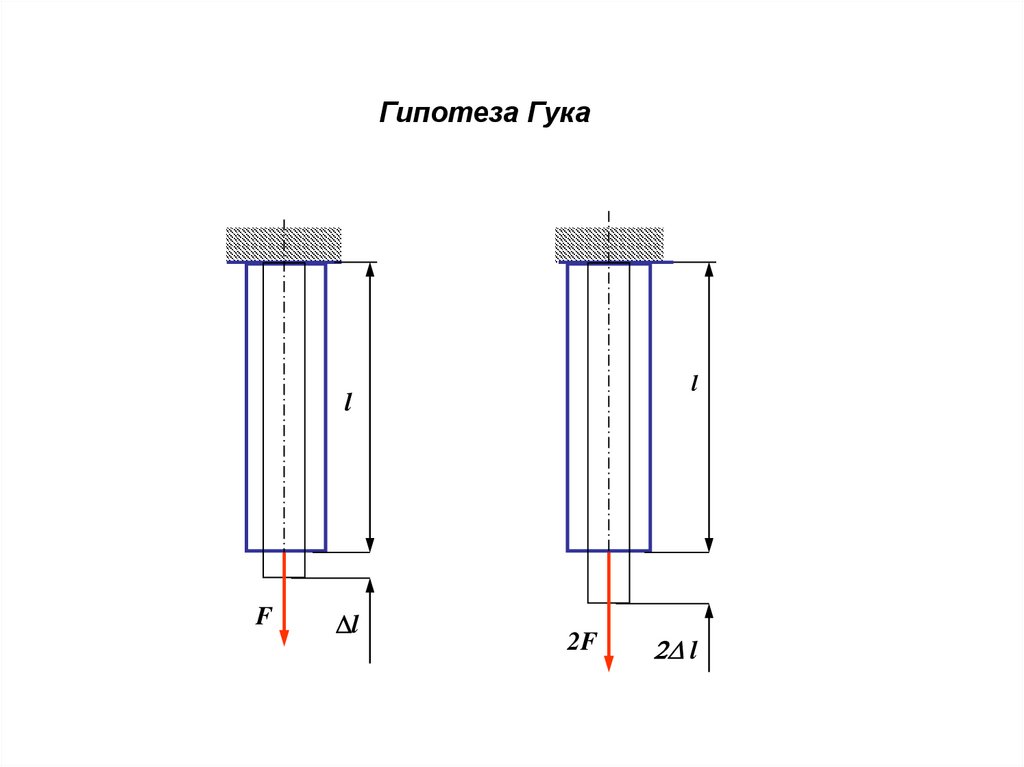
4.Гипотеза о совершенной упругости
материала – перемещения точек
конструкции в упругой стадии работы
материала прямо пропорциональны силам
, вызывающим эти перемещения
(справедлив закон Гука);

31.

Гипотеза Гука
l
l
F
l
2F
l

32.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
5. Гипотеза Бернулли о плоских
сечениях –
поперечные сечения, плоские и
нормальные к оси стержня до приложения
к нему нагрузки, остаются плоскими и
нормальными к его оси в
деформированном состоянии; при изгибе
сечения поворачиваются не искривляясь.

33.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
6. Принцип Сен-Венана – в точках
тела, достаточно удалённых от места
приложения нагрузок, внутренние
силы весьма мало зависят от
конкретного способа приложения этих
нагрузок.

34.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
7. Принцип Д’Аламбера – если к
активным силам, действующим на
точки механической системы, и
реакциям наложенных связей
присоединить силы инерции, то
получится уравновешенная
система сил.
Принцип используется в расчетах на прочность
при динамическом действии сил.

35.

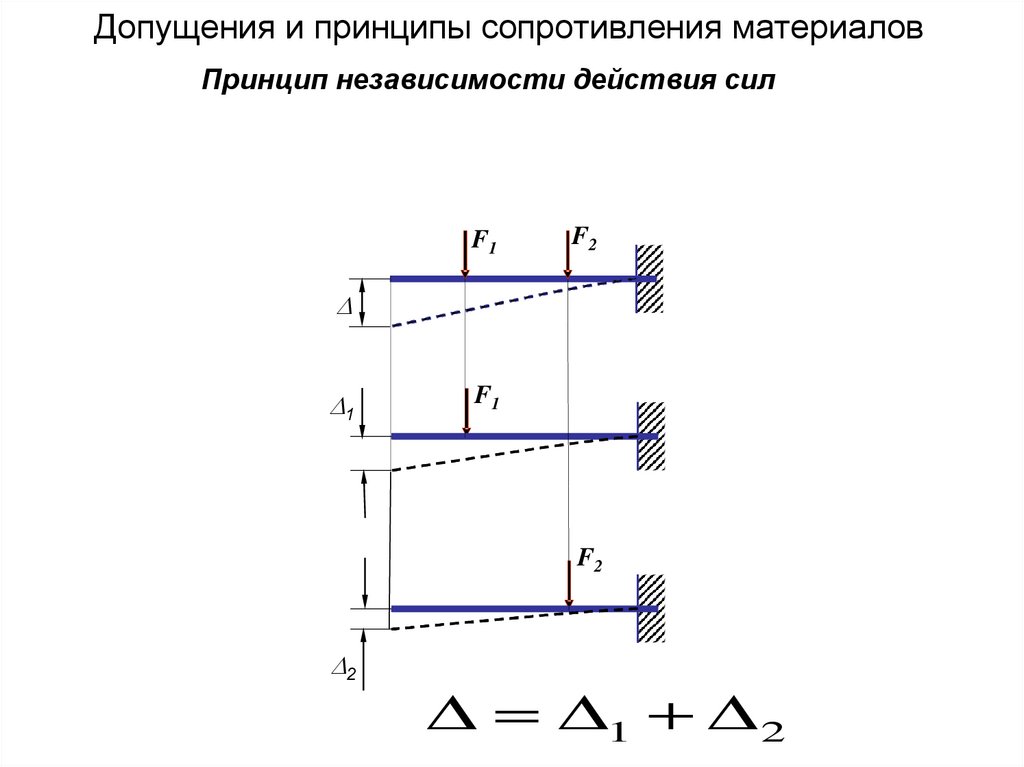
ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
8. Принцип независимости
действия сил (принцип
суперпозиции) – результат
воздействия нескольких внешних
факторов равен сумме результатов
воздействия каждого из них,
прикладываемого в отдельности, и
не зависит от последовательности
их приложения.
Это же справедливо и в отношении
деформаций.

36.

Допущения и принципы сопротивления материалов
Принцип независимости действия сил
F1
F2
1
F1
F2
2
1 2

37.

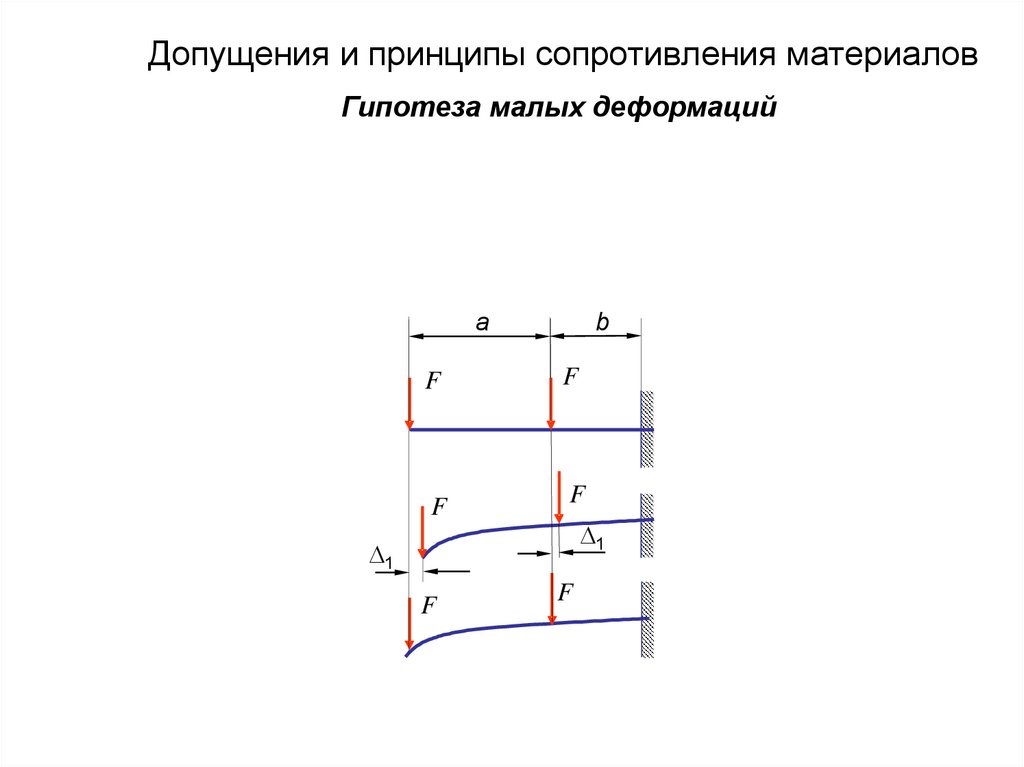
ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
9. Принцип начальных размеров
(гипотеза о малости деформаций) –
деформации в
точках тела настолько малы по
сравнению с размерами
деформируемого тела, что не
оказывают существенного влияния
на взаимное расположение нагрузок,
приложенных к телу.
Допущение применяют при составлении
условий статики, считая тело абсолютно

38.

Допущения и принципы сопротивления материалов
Гипотеза малых деформаций
a
b
F
F
F
F
1
1
F
F

39.

ГИПОТЕЗЫ И ДОПУЩЕНИЯ, ПРИНЯТЫЕ
В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
10. Допущение об отсутствии
начальных
внутренних усилий в теле до
приложения

40.

• Внешние силы –это результат
действия на тело других тел или
внешней среды;
• Внутренние силы – это усилия,
возникающие между всеми
соседними частицами внутри тела,
под воздействием нагрузки
(внешних сил).
40

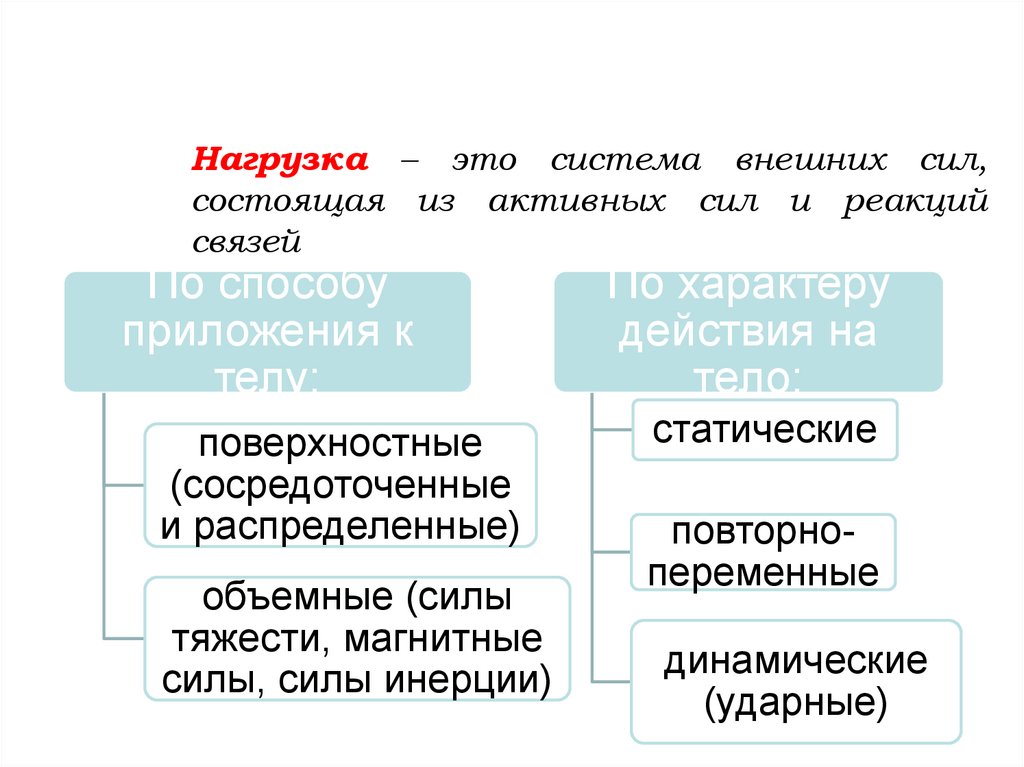
41.

Нагрузка – это система внешних сил,
состоящая из активных сил и реакций
связей
По способу
приложения к
телу:
поверхностные
(сосредоточенные
и распределенные)
объемные (силы
тяжести, магнитные
силы, силы инерции)
По характеру
действия на
тело:
статические
повторнопеременные
динамические
(ударные)

42.

По ХАРАКТЕРУ (времени) действия различают:
1.Статическую нагрузку – если она плавно
меняется от нуля до конечного значения;
возникающие силы инерции малы и ими можно
пренебречь.
2.Динамическую нагрузку:
а) мгновенно приложенную нагрузку – если она
изменяется от нуля до конечного значения за
доли секунды.
б) ударную нагрузку – если тело, вызывающее
нагрузку, обладает кинетической энергией.
3. Повторно-переменную нагрузку – если она
меняется по времени.

43.

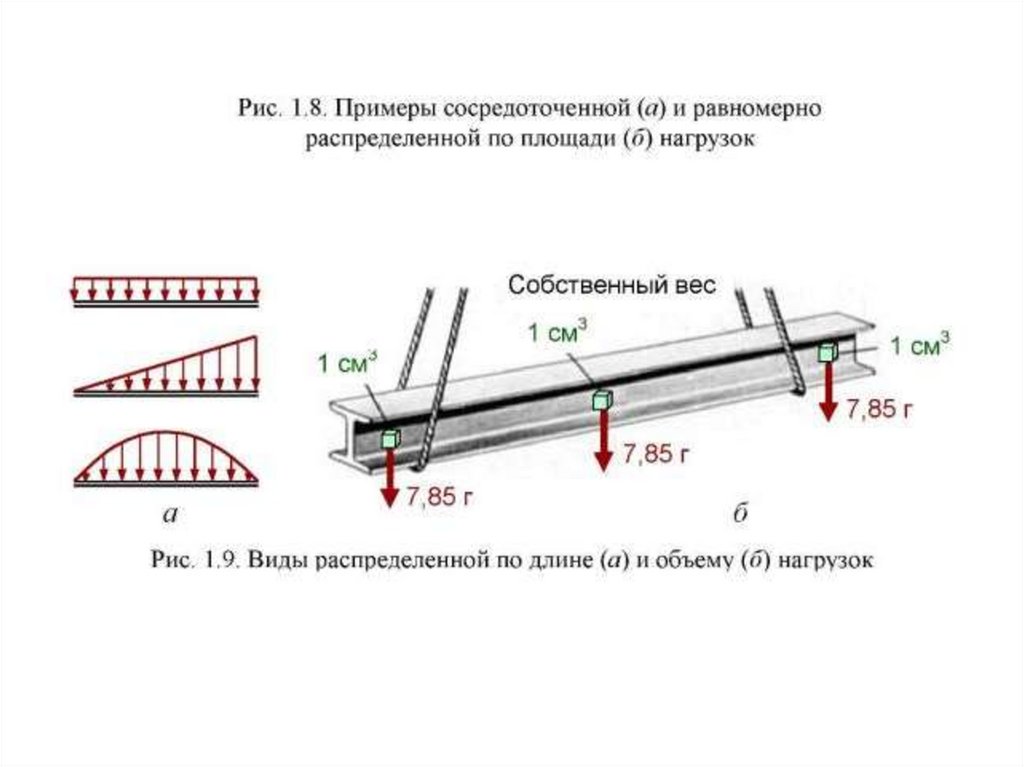
Внешние силы разделяются на
поверхностные и объёмные.
Объемные
(массовые)
силы
приложены к каждой частице объема
(массы) материала.
Поверхностные силы – это силы,
распределенные определенным образом
по поверхности тела.
43

44.

45.

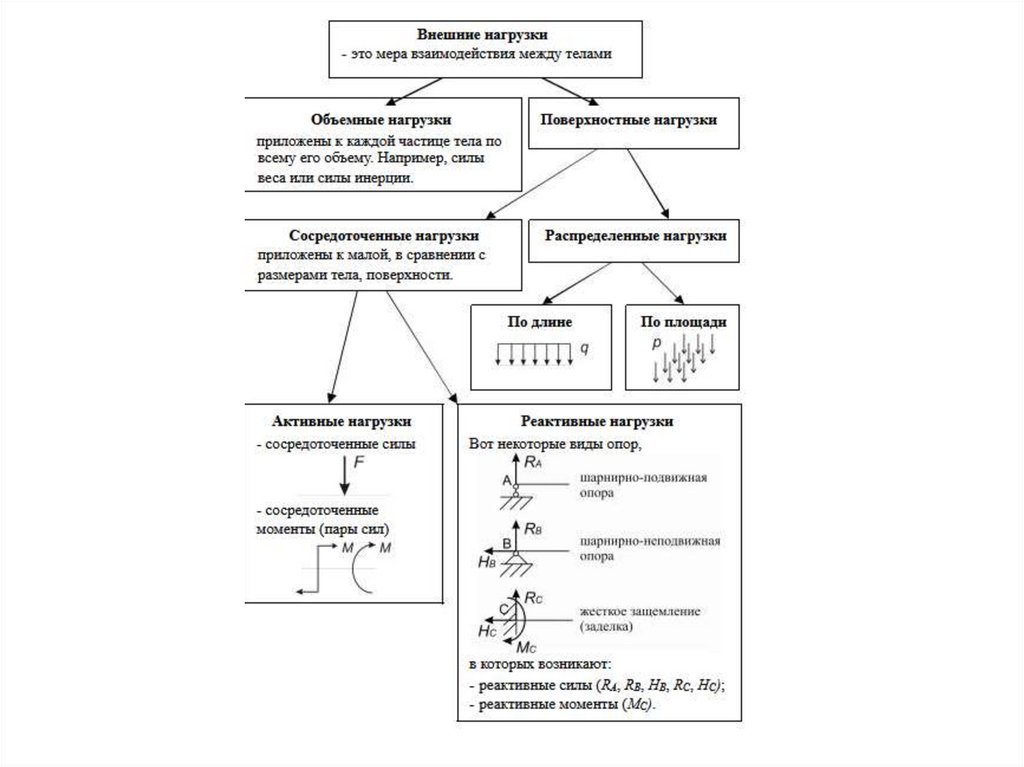
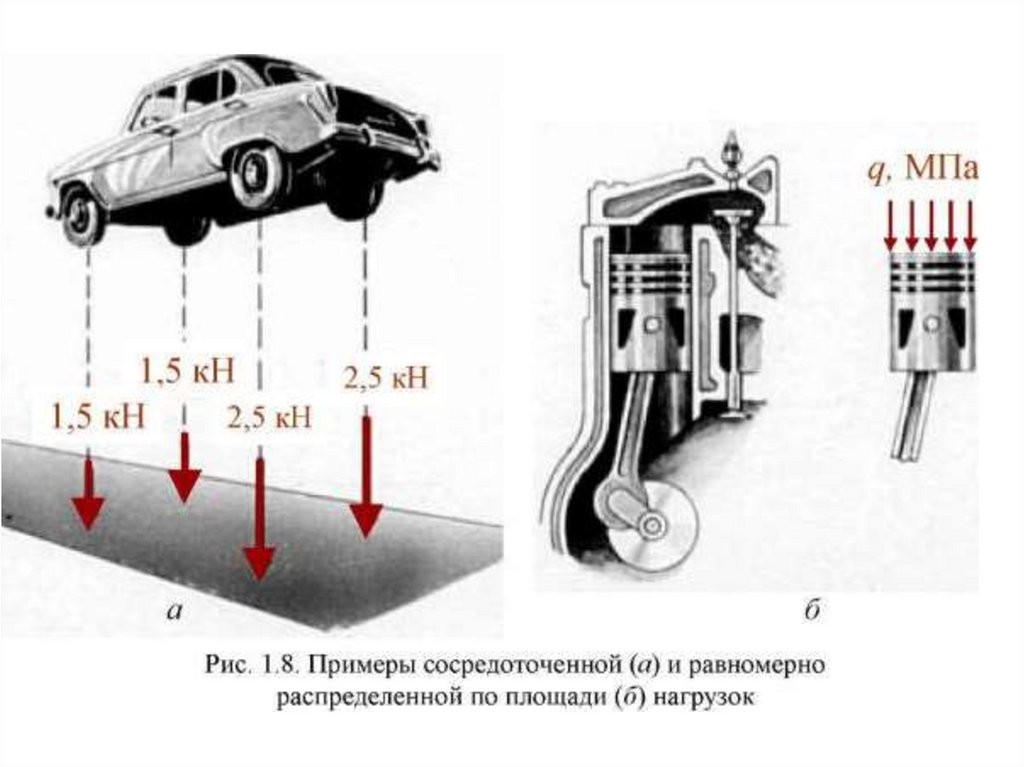
Классификация внешних сил
Внешние силы (нагрузка) подразделяются на
распределенные и сосредоточенные.
Распределенной нагрузкой называется нагрузка,
приложенная к значительным участкам поверхности
тела.
Распределенная нагрузка подразделяется на
равномерно и произвольно распределенную по длине
либо по некоторой площади поверхности тела
q Н м
Размерность интенсивности нагрузки, распределенной
по длине поверхности тела
45

46.

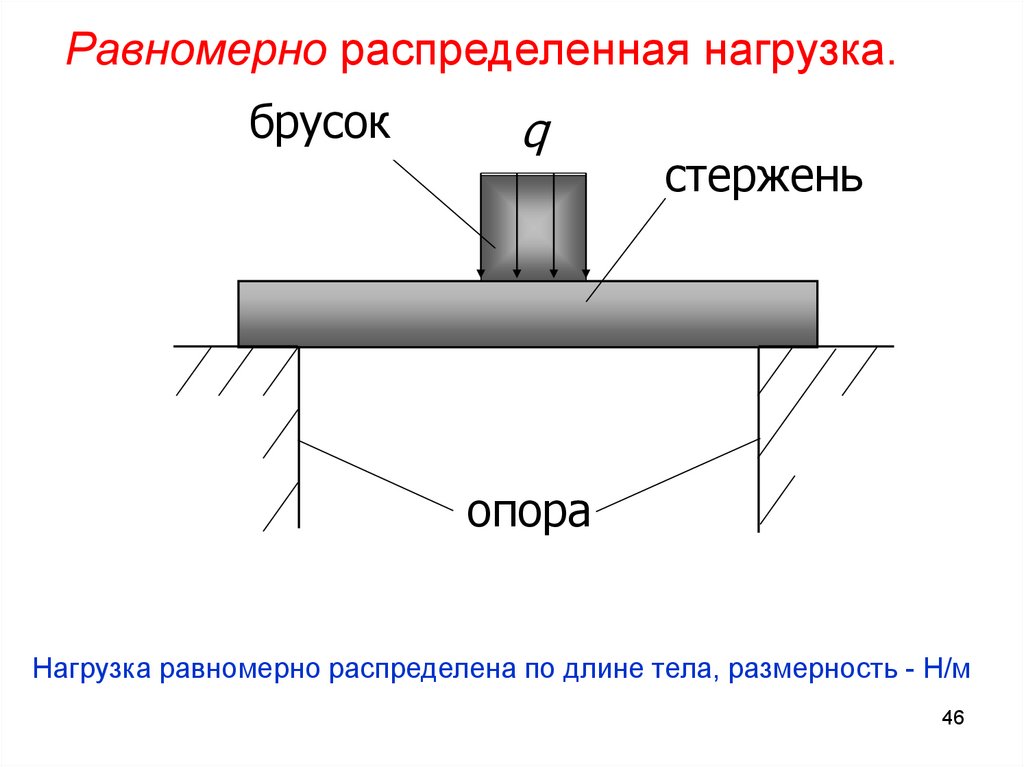
Равномерно распределенная нагрузка.
брусок
q
стержень
опора
Нагрузка равномерно распределена по длине тела, размерность - Н/м
46

47.

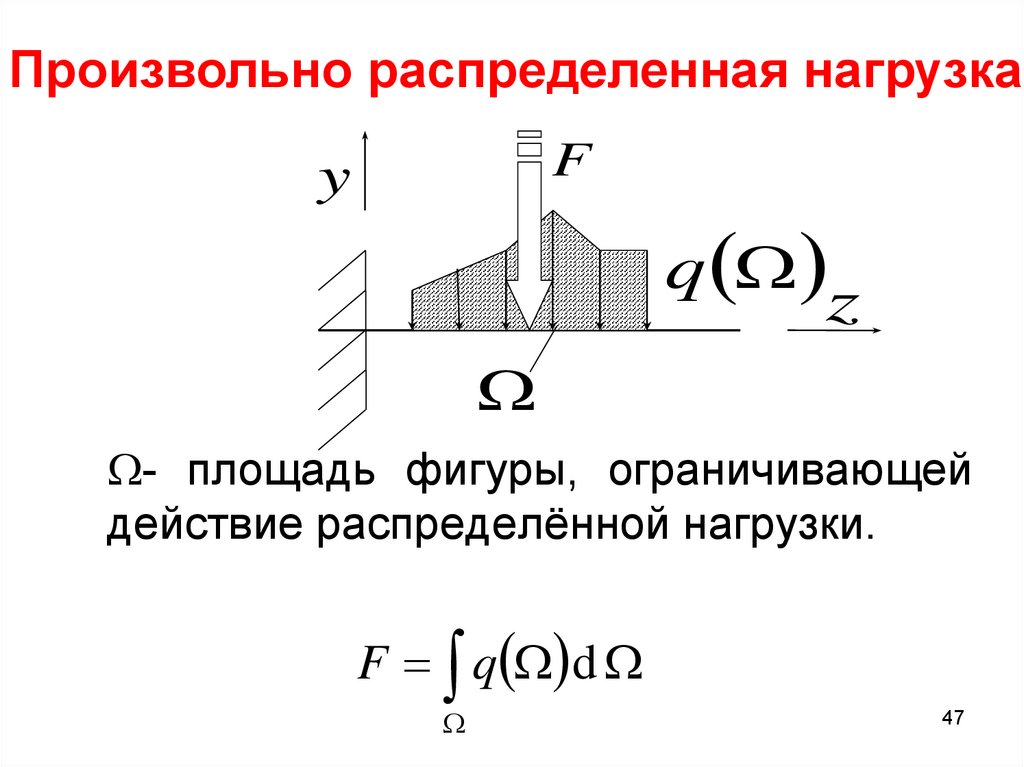
Произвольно распределенная нагрузка.
F
y
q
z
- площадь фигуры, ограничивающей
действие распределённой нагрузки.
F q d
47

48.

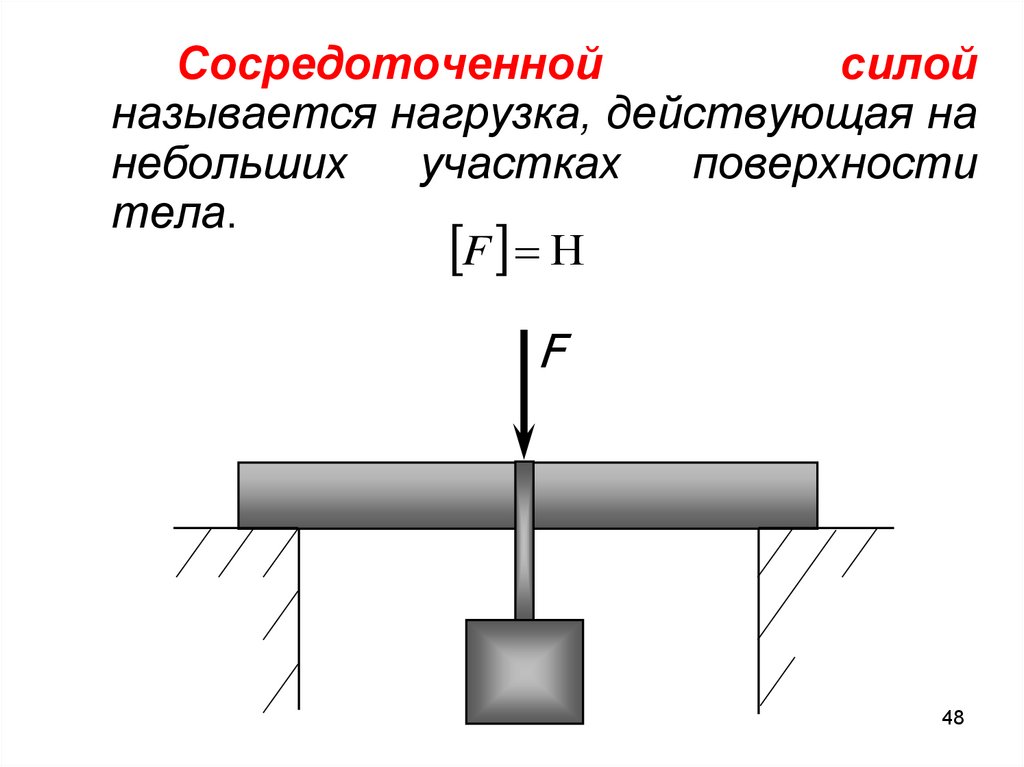
Сосредоточенной
силой
называется нагрузка, действующая на
небольших
участках
поверхности
тела.
F Н
F
48

49.

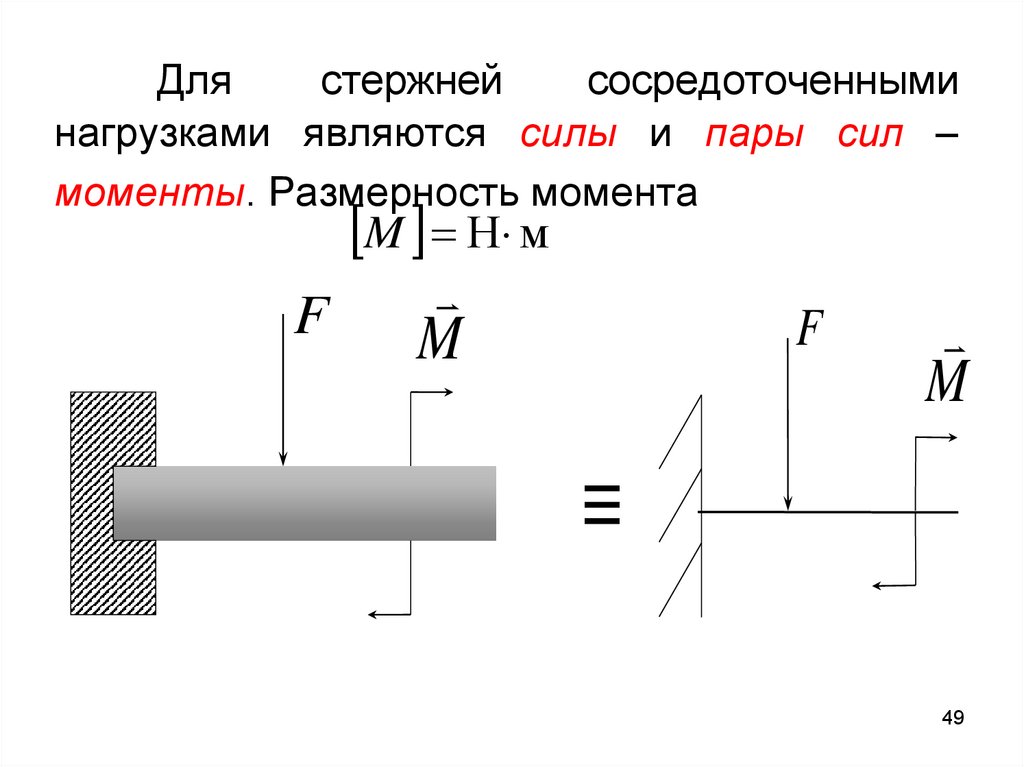
Для
стержней
сосредоточенными
нагрузками являются силы и пары сил –
моменты. Размерность момента
M Н м
F
M
F
M
49

50.

51.

52.

ВНУТРЕННИЕ УСИЛИЯ. МЕТОД
СЕЧЕНИЙ
Внутренние усилия –
силы взаимодействия между
частицами тела (кристаллами,
молекулами, атомами), возникающие
внутри элемента конструкции, как
противодействие внешним нагрузкам.

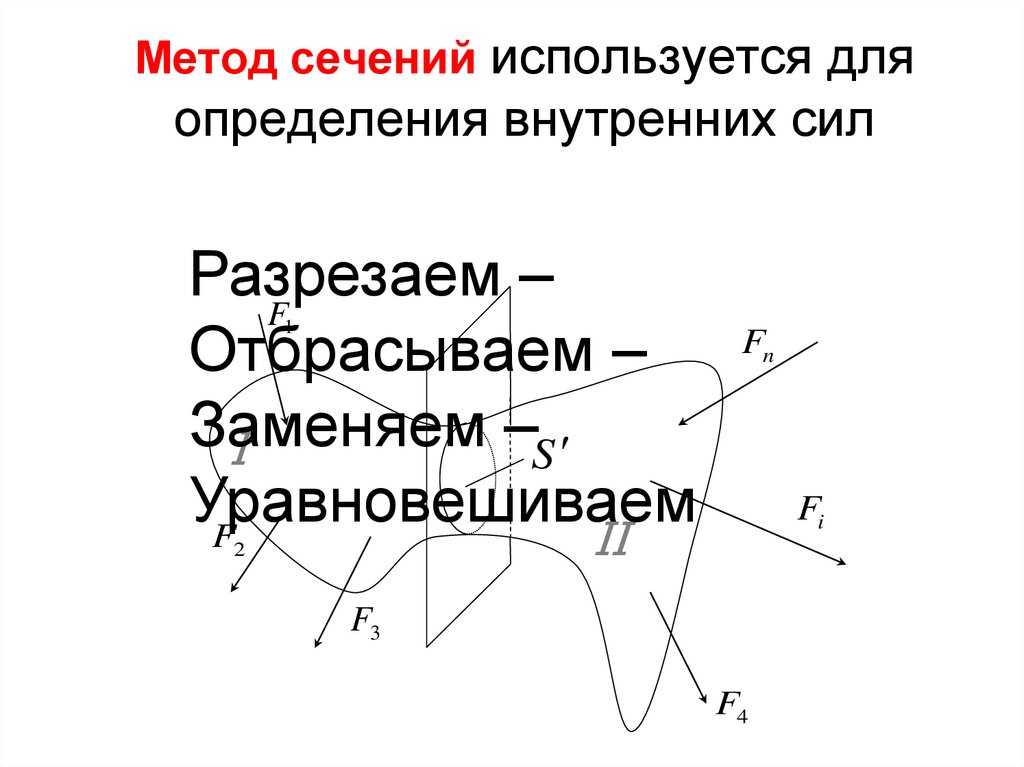
53.

Метод сечений используется для
определения внутренних сил
Разрезаем
–
F
F
Отбрасываем –
Заменяем
–S
I
F
Уравновешиваем
F
1
n
II
2
i
F3
F4

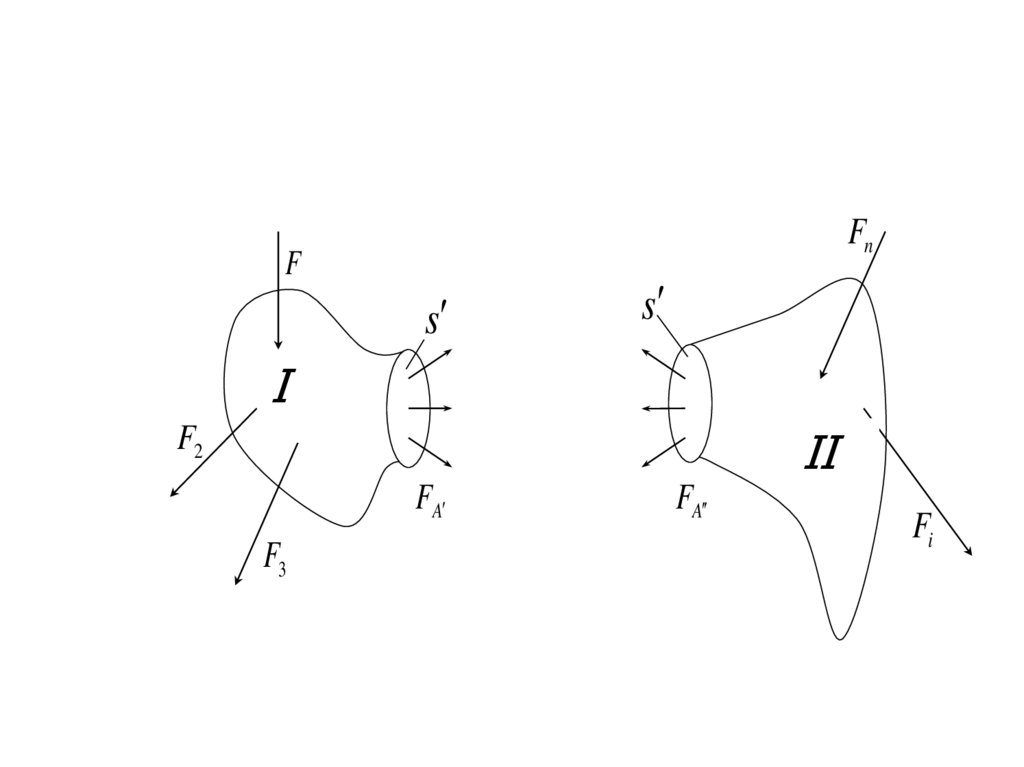
54.

Fn
F
s
s
I
II
F2
FA
F3
FA
Fi

55.

Для внутренних силовых факторов приняты
следующие названия:
N - продольная или осевая сила;
Qy и Qх – поперечные силы;
Мк - крутящий момент;
M y моменты
Мy и Mх - изгибающие
y
Qy
F1
Qx
F2
F3
x
Mx
R
M
z
N
Mk

56.

Для определения внутренних силовых
факторов можно составить уравнения
равновесия для левой и правой частей:
n
n
n
N Fiz ;
Qx Fix ;
Qy Fiy ;
n
n
n
i 1
i 1
i 1
i 1
i 1
i 1
M z m0 z Fi ; M x m0 x Fi ; M y m0 y Fi .
Правило определения внутренних силовых
факторов: внутренние силы N, Qy, Qz
численно равны алгебраической сумме
проекций всех внешних сил (в том числе и
реакций), приложенных к брусу по одну
сторону от рассматриваемого сечения.

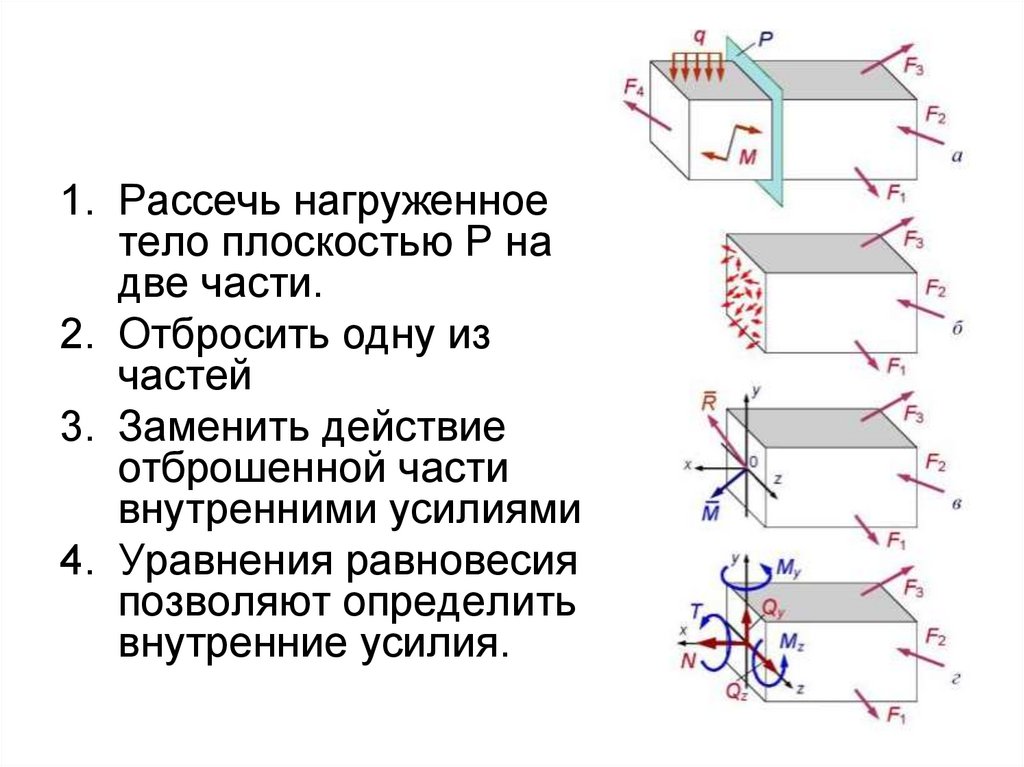
57.

1. Рассечь нагруженное
тело плоскостью Р на
две части.
2. Отбросить одну из
частей
3. Заменить действие
отброшенной части
внутренними усилиями
4. Уравнения равновесия
позволяют определить
внутренние усилия.

58.

ПОНЯТИЕ О НАПРЯЖЕНИЯХ
• Напряжение в точке по сечению –
внутренняя сила взаимодействия,
приходящаяся на единицу площади у
этой точки.
• Напряжение – величина,
характеризующая интенсивность
внутренних усилий в точке.

59.

• Напряжение нормальное σ, σн –
перпендикулярное к сечению,
характеризует интенсивность
сил отрыва или сжатия частиц
элементов конструкции.

60.

• Напряжение касательное τ, στ–
действующее в плоскости
сечения, характеризует
интенсивность сил, сдвигающих
эти части в плоскости сечения.

61.

• Единица измерения давления и
механического напряжения паскаль
(обозначение Па).
Паскаль – давление, вызываемое силой 1 Н,
равномерно распределенной по поверхности
площадью 1 м2.
• 1 Па = 1 Н/м2;
• 1 МПа = 0,102 кгс/мм2;
• 1 МПа = 10,2 кгс/см2;
• 1 МПа = 1 Н/мм2;
• 1 кгс/мм2 = 9,81 МПа.

62.

Понятие
напряжения
dR
dQ
F1
dN
dA
Полным механическим напряжением называют
отношение равнодействующей внутренних сил dR
действующей на малый элемент выбранного
сечения к площади этого элемента dA.
р
F2
Fn
Нормальным напряжением называется отношение
нормальных сил dN действующих на малый элемент
выбранного сечения к площади этого сечения dA:
p
F1
F2
dA
Fn
dR
lim
dA 0 dA
dN
dA 0 dA
lim
Касательным напряжением называется отношение
касательных сил dQ действующих на малый элемент
выбранного сечения к площади dA этого элемента.
dQ
dA 0 dA
lim
Нормальные и касательные напряжения являются составляющими
полного напряжения р:
р
2 2

63.

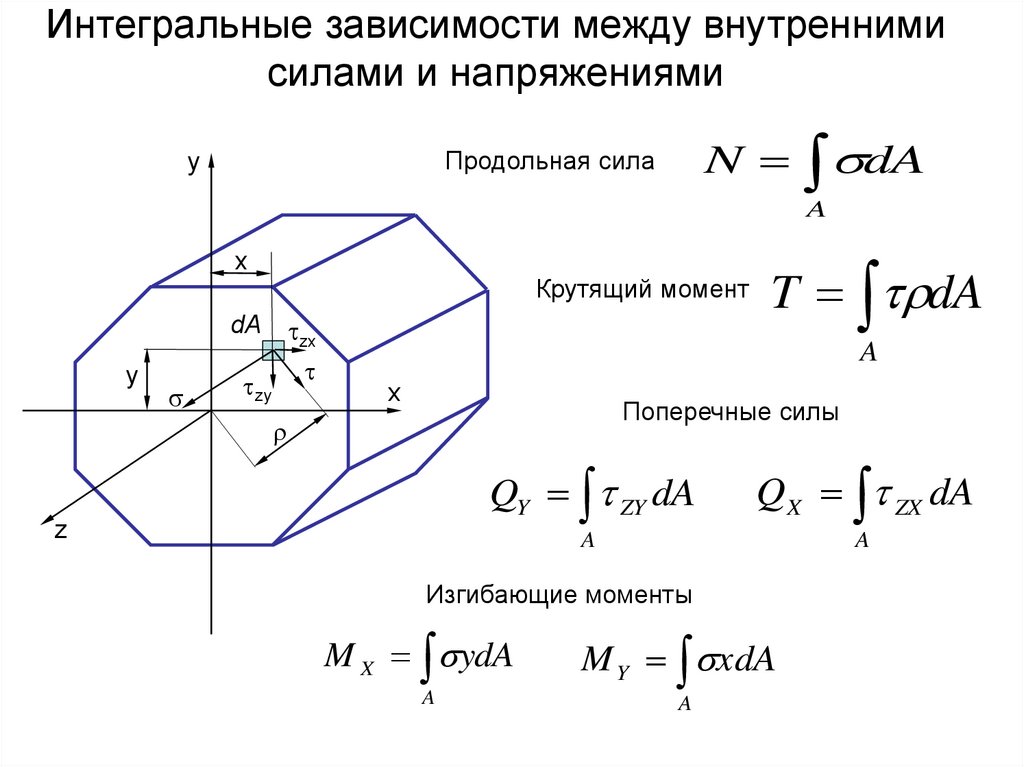
Интегральные зависимости между внутренними
силами и напряжениями
N dA
Продольная сила
y
A
x
Крутящий момент
zx
dA
y
zy
T dA
A
x
Поперечные силы
QY ZY dA
z
Q X ZX dA
A
Изгибающие моменты
M X ydA
A
M Y xdA
A
A

64.

ВИДЫ ДЕФОРМАЦИЙ И
ДЕФОРМИРОВАНИЯ
• Растяжение (сжатие) – вид сопротивления
(деформирования), при котором из шести
внутренних усилий не равно нулю одно –
продольное усилие N.
• Сдвиг – вид сопротивления
(деформирования), характеризующийся
взаимным смещением параллельных слоев
материала под действием приложенных сил
при неизменном расстоянии между слоями.
Внутреннее усилие одно – поперечная сила Q.

65.

ВИДЫ ДЕФОРМАЦИЙ И
ДЕФОРМИРОВАНИЯ
• Кручение – вид сопротивления
(деформирования), при котором из шести
внутренних усилий не равно нулю одно –
крутящий момент Т.
• Изгиб – вид сопротивления
(деформирования), при котором происходит
искривление оси прямого бруса, или
изменение кривизны кривого бруса.

66.

Деформации и перемещения.
Деформация – изменение формы и размеров тела в
результате действия внешних нагрузок.
в/2
в
F
а
a
Любая деформация элементов тела может быть
разложена на два вида элементарных
деформаций: линейные и угловые.

67.

Деформации и перемещения.
Линейными называются деформации, при которых
происходит изменение линейных размеров бруса, а все
угловые соотношения остаются неизменными.
в/2
в
F
а
a
Приращение длины ребра бруса после
деформации а ( в) называется абсолютным
удлинением (укорочением).

68.

Деформации и перемещения.
Мерой линейной продольной деформации
является относительное удлинение, ,
которое равно отношению абсолютного
удлинения бруса, а к начальному
размеру а:
а
а

69.

Деформации и перемещения.
а
F
g
а
s
Угловыми называются деформации, при
которых изменяются углы между ребрами
бруса за счет сдвига одной плоскости
элемента относительно другой.
Величина перемещения любой точки в
плоскости сдвига s, называется
абсолютным сдвигом.
Мерой угловой деформации является относительный сдвиг, g, который
равен отношению абсолютного сдвига s к расстоянию между плоскостями
сдвига а:
s
g
а

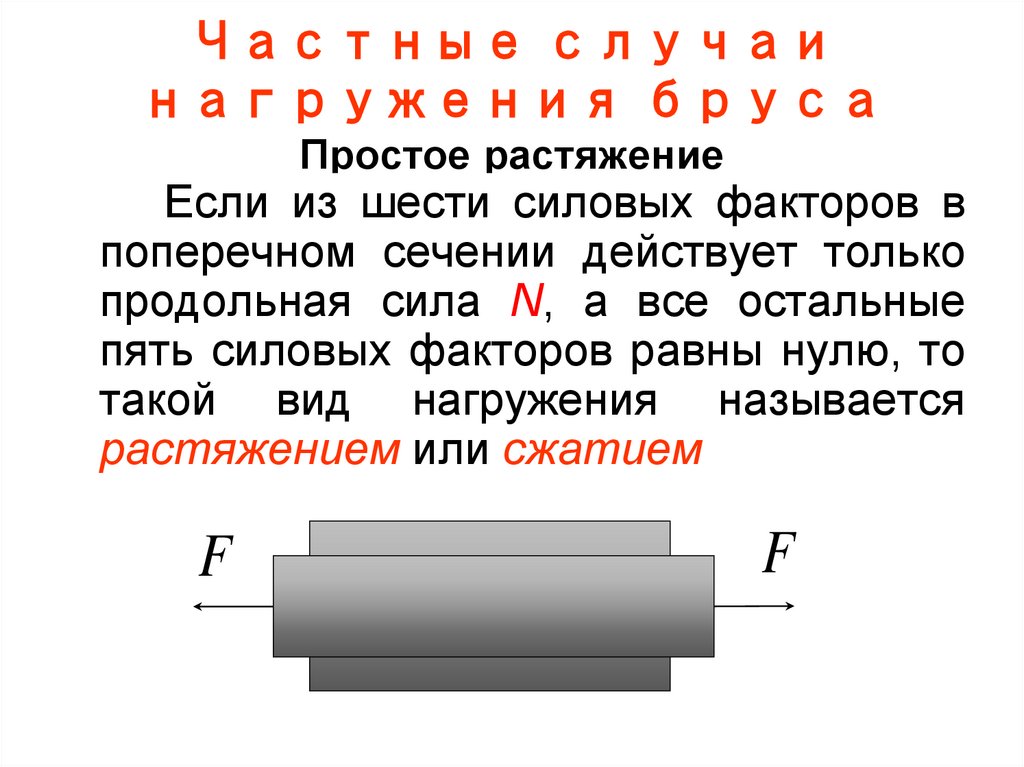
70.

Частные случаи
нагружения бруса
Простое растяжение
Если из шести силовых факторов в
поперечном сечении действует только
продольная сила N, а все остальные
пять силовых факторов равны нулю, то
такой вид нагружения называется
растяжением или сжатием
F
F

71.

Если внешняя сила F действует от сечения,
то она вызывает растяжение (увеличение
длины бруса) и сила N в сечении считается
положительной (N > 0 – растяжение).
Если внешняя сила F действует к сечению,
то она вызывает сжатие (уменьшение длины
бруса) и сила N в сечении считается
отрицательной (N < 0 – сжатие).
Брусья, в основном работающие на
растяжение-сжатие, называются
стержнями.

72.

Сдвиг
Если из шести силовых факторов в
проведённом сечении действует только
поперечная сила Qx или Qy, а все
остальные пять силовых факторов
равны нулю, то такой вид нагружения
называется сдвигом
F
F
F
F

73.

Кручение
Кручением
называется
такой
вид
нагружения бруса, при котором в его поперечном
сечении возникает только один внутренний
силовой фактор, отличный от нуля, крутящий
момент Mz или Мкр.
Примером детали, работающей на кручение, является вал.
Mz
Mz
При действии разнонаправленных
крутящих моментов одинаковой величины
в противоположных торцах вала, он будет
закручиваться, сечения вала будут
поворачиваться относительно друг друга,
а
длина
вала
будет
оставаться
неизменной.

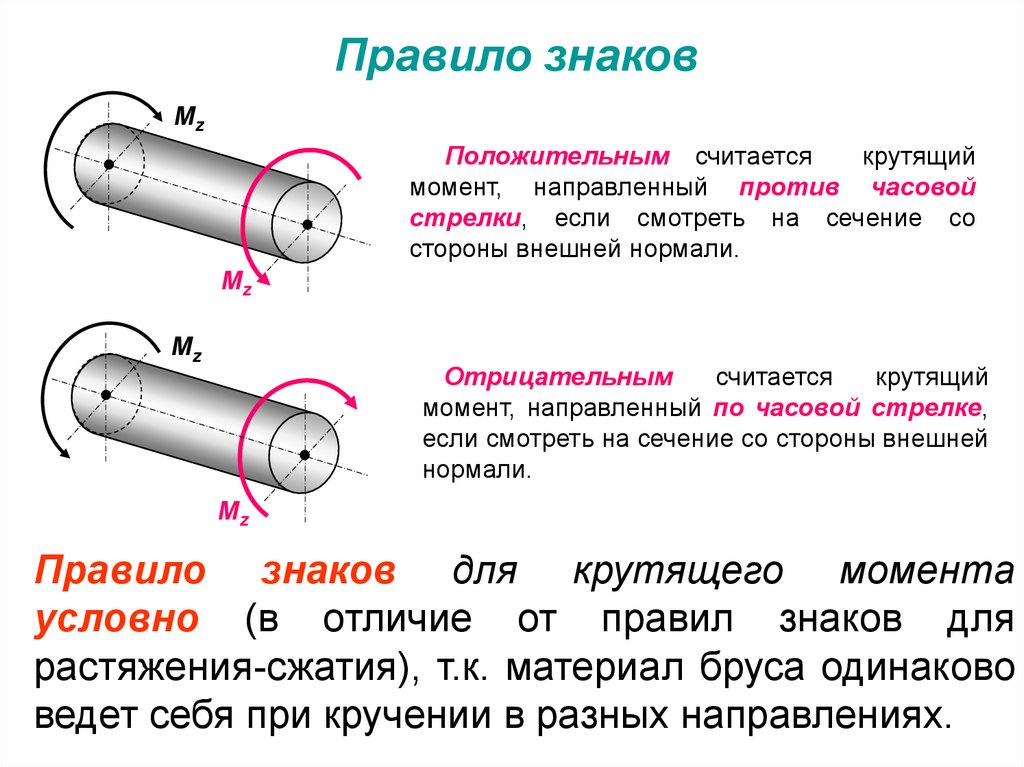
74.

Правило знаков
Mz
Положительным считается
крутящий
момент, направленный против часовой
стрелки, если смотреть на сечение со
стороны внешней нормали.
Mz
Mz
Отрицательным
считается
крутящий
момент, направленный по часовой стрелке,
если смотреть на сечение со стороны внешней
нормали.
Mz
Правило знаков для крутящего момента
условно (в отличие от правил знаков для
растяжения-сжатия), т.к. материал бруса одинаково
ведет себя при кручении в разных направлениях.

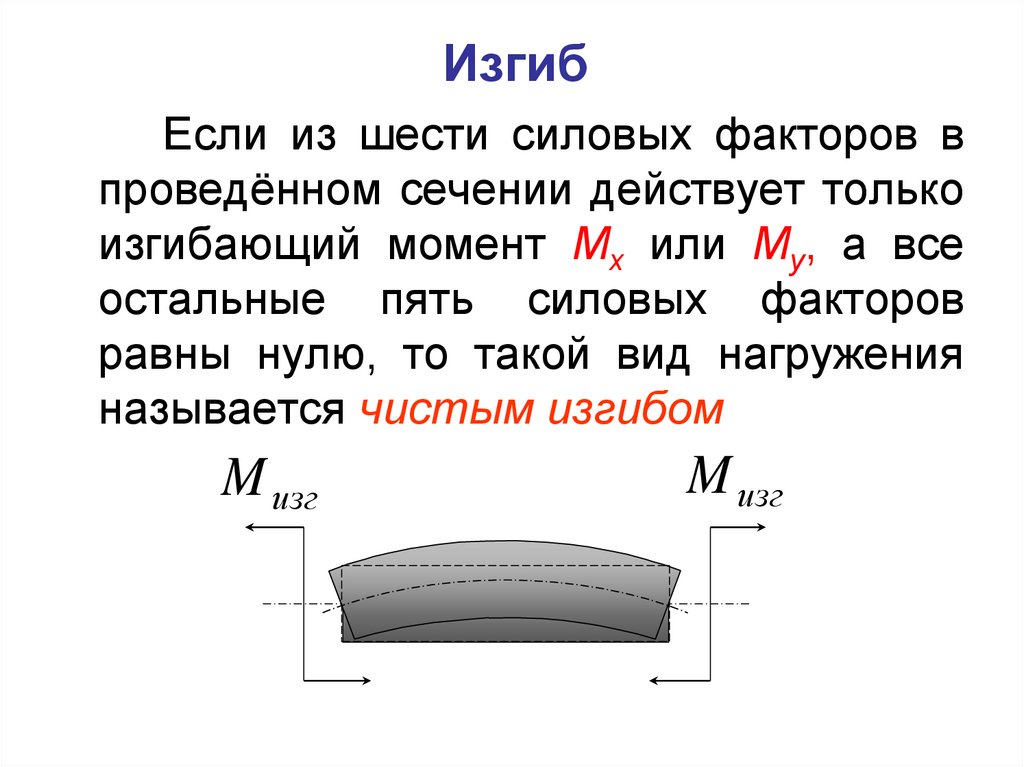
75.

Изгиб
Если из шести силовых факторов в
проведённом сечении действует только
изгибающий момент Mx или My, а все
остальные пять силовых факторов
равны нулю, то такой вид нагружения
называется чистым изгибом
M изг
M изг

76.

Если из шести силовых факторов в
проведённом
сечении
действует
только изгибающий момент Mx и
поперечная сила Qy или My и Qx, а все
остальные четыре силовых фактора
равны нулю, то такой вид нагружения
называется поперечным изгибом.
В остальных случаях нагружение
называется сложным нагружением
или сложным сопротивлением.

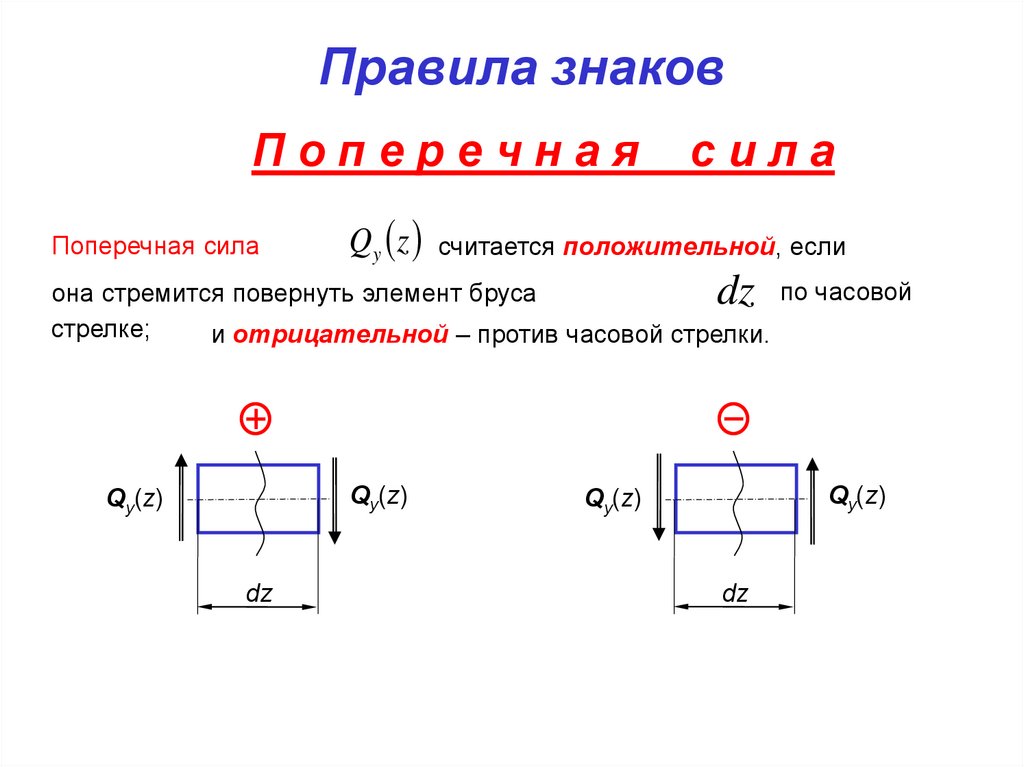
77.

Правила знаков
Поперечная
Поперечная сила
сила
Qy z считается положительной, если
dz
по часовой
она стремится повернуть элемент бруса
стрелке;
и отрицательной – против часовой стрелки.
Qy(z)
Qy(z)
dz
Qy(z)
Qy(z)
dz

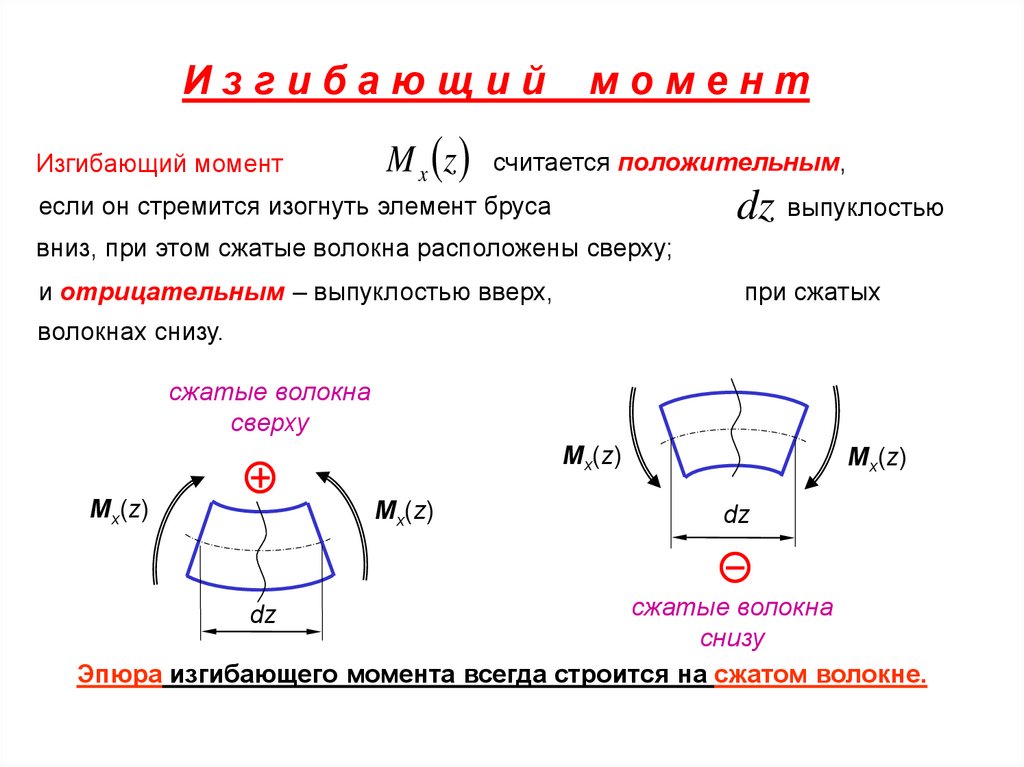
78.

Изгибающий
Изгибающий момент
момент
M x z считается положительным,
dz выпуклостью
если он стремится изогнуть элемент бруса
вниз, при этом сжатые волокна расположены сверху;
и отрицательным – выпуклостью вверх,
при сжатых
волокнах снизу.
сжатые волокна
сверху
Mx(z)
Mx(z)
Mx(z)
Mx(z)
dz
сжатые волокна
снизу
Эпюра изгибающего момента всегда строится на сжатом волокне.
dz

79.

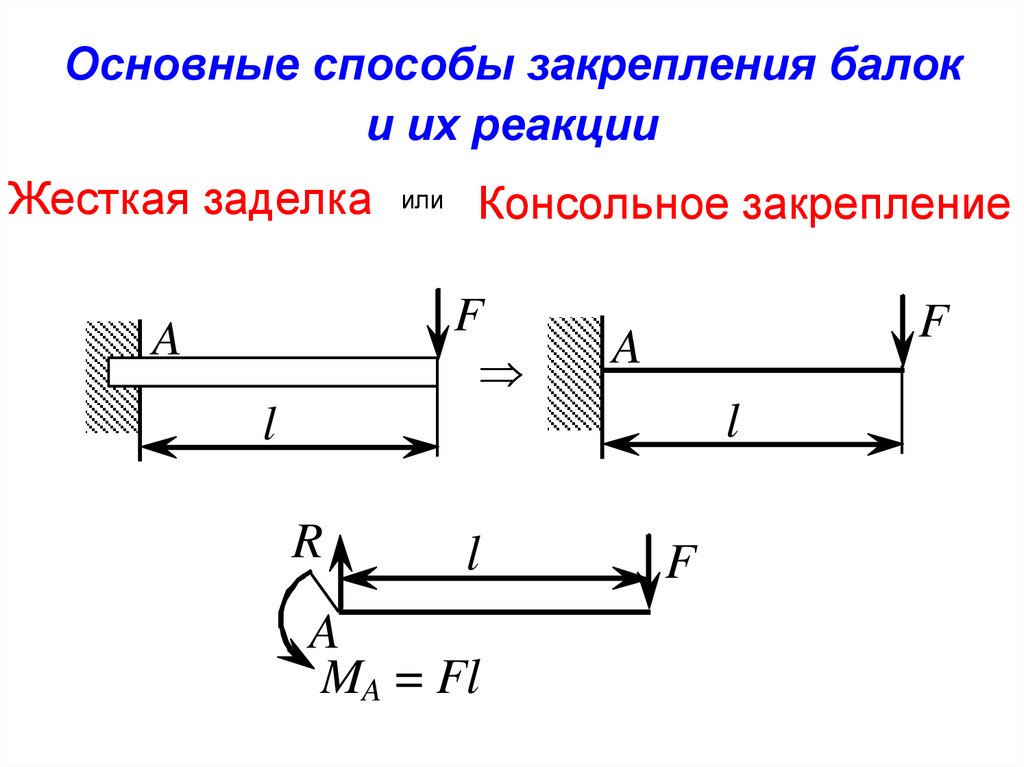
Основные способы закрепления балок
и их реакции
Жесткая заделка или Консольное закрепление
F
A
F
A
l
l
R
l
A
MA = Fl
F
F

80.

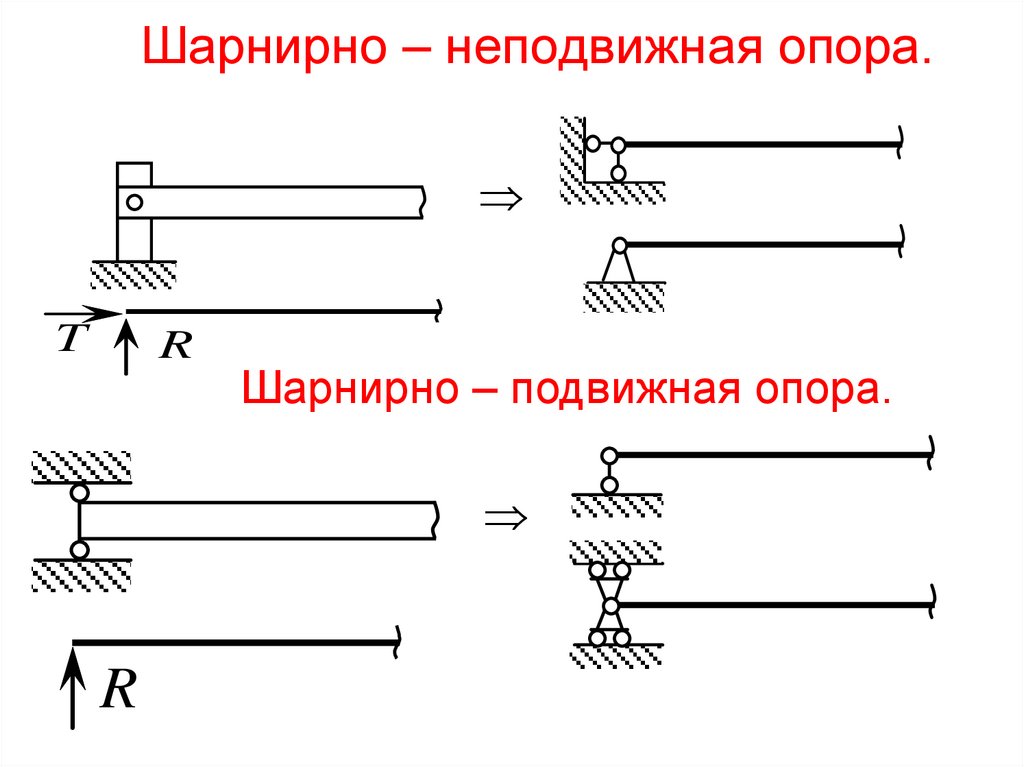
Шарнирно – неподвижная опора.
T
R
Шарнирно – подвижная опора.
R

81.

Определение опорных реакций.
Для плоской системы можно составить три уравнения
равновесия:
n
1. Fу 0
i 1
n
2. Fх 0
i 1
n
3. M B 0
i 1
Правила знаков:
Силы, направленные вверх, считаются положительными (+),
-
вниз – отрицательными ( )
Моменты сил, направленные по часовой стрелке, считаются
отрицательными (-), против – положительными (+)

82.

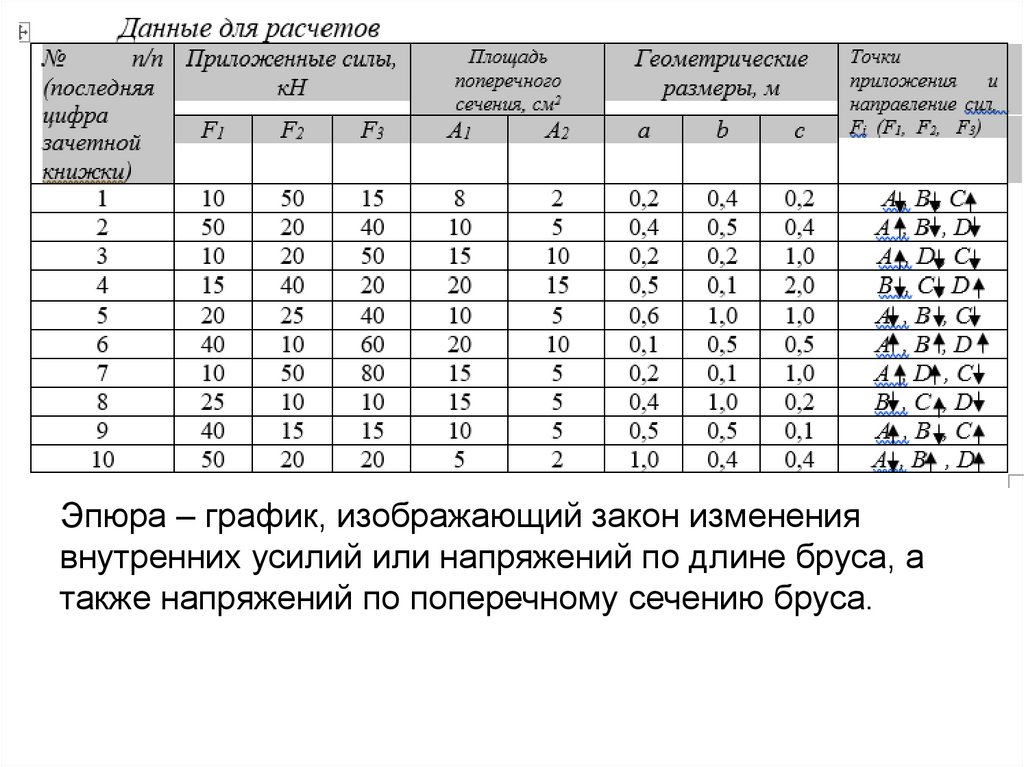
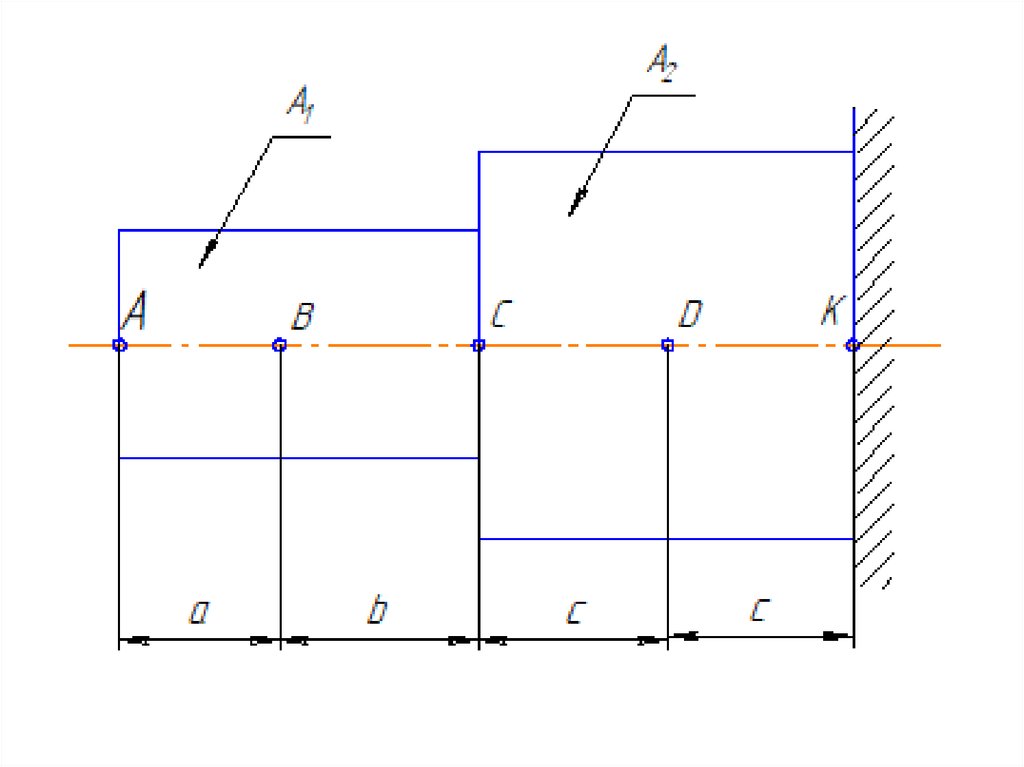
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОГО
СТУПЕНЧАТОГО СТЕРЖНЯ БЕЗ УЧЕТА
СОБСТВЕННОГО ВЕСА
Дано: двухступенчатый стержень,
на который
действуют активные силы F1; F2 и F3; площади
поперечных сечений А1 и А2. Стержень изготовлен из
стали Ст.3. Допускаемое напряжение на растяжение и
сжатие для стали Ст. 3