13-Презентация+ДЗ-В-9

1.

Испытание. Успех и
неудача. Серия
испытаний до первого
успеха

2.

Испытание — основное понятие в теории
вероятности.
Под испытанием подразумевают действие,
которое может повторяться неопределённое
количество раз при неизменных условиях.
Термин «испытание» ассоциируют с Бернулли.
Яков Бернулли изучал серии испытаний, которые
оказались важными для науки.
Испытание Бернулли — случайный опыт,
который может закончиться одним из двух
элементарных событий.

3.

Под двумя элементарными событиями
подразумевают несовместные взаимно
противоположные исходы события. Данные
исходы условно называют «успехом» или
«неуспехом».
Испытание Бернулли, которое завершится успехом, будем
обозначить буквой p.
Испытание Бернулли, которое завершится неуспехом,
будем обозначить буквой q.

4.

Из формулы следует,
что успех — это разность неуспеха от единицы: p=1−q,
а неуспех — это разность успеха от единицы: q=1−p.
Считается, что и успех, и неуспех не могут быть меньше
нуля и больше единицы:
0<p<1,
0<q<1.
Результатом испытания является случайное событие.
Случайное событие может произойти или не произойти.

5.

ПРИМЕР:
Примером случайного события может быть
получение оценки в школе. Ученик может получить
оценку «пять», а может и не получить.
Случайные события состоят из множества элементарных
событий.
Элементарные события — это возможные,
исключающие друг друга, результаты испытаний. На
более простые события элементарные события не
раскладываются.

6.

Проанализируем серию испытаний до
наступления первого успеха. При наступлении успеха
серия испытаний прекращается.
ПРИМЕР:
Собирать кубик Рубика, пока не собрались все грани
одного цвета.
Пытаться забить гол в ворота соперника.
При стрельбе из лука попасть в мишень.
Найти выход из лабиринта.

7.

Условия проведения испытаний:
1) независимость испытаний;
2) вероятность успеха равна p.
Исследуя случайный опыт, получим некую
последовательность элементарных событий.
Обозначим успех буквой У, неуспех — буквой Н.
Последовательность элементарных событий может
быть У, НУ, ННУ, НННУ, ННННУ, НННННУ и т. д.
Теоретически получаем бесконечное множество
элементарных событий.

8.

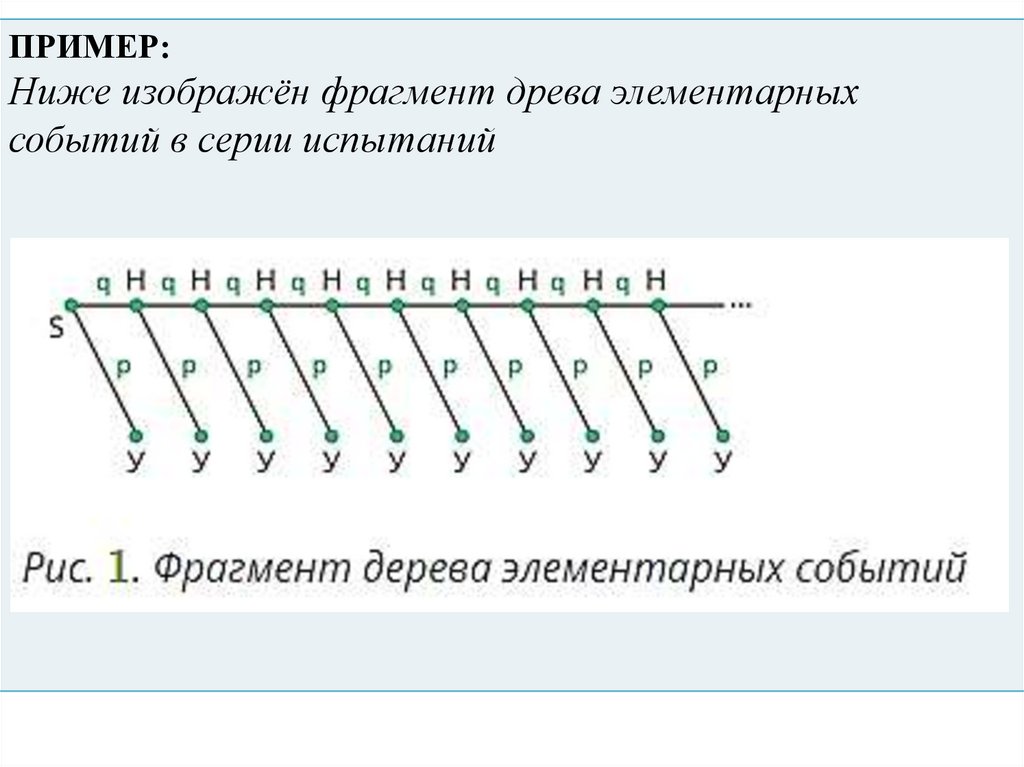
ПРИМЕР:
Ниже изображён фрагмент древа элементарных
событий в серии испытаний

9.

ПРИМЕР:
Цепочка элементарных событий из начальной точки S к
конечным вершинам У.

10.

Вероятность каждого элементарного события находим,
используя правило умножения, где P(У) = p,
P(НУ) = q⋅p,
P(ННУ)= q⋅q⋅p=q2⋅p,
P(НННУ)= q⋅q⋅q⋅p=q3p и так далее, пока не наступит успех.
Для нахождения вероятности успеха в нескольких
элементарных исследованиях формула будет следующей:
P(A)=1−qn, где
A — это благоприятствующие элементарные
события У, НУ, ННУ, НННУ…
n — количество попыток всего.

11.

Задание 1
Вероятность успеха в серии испытаний
равна 0,77. Найди вероятность неуспеха.
Задание 2
Для экзамена необходимо повторить решение 75 типов
задач. Григорий успел повторить только 39. Найди
вероятность того, что Григорию придётся решать на
экзамене задачу, которую он не успел повторить.
(Ответ округли до сотых.)

12.

Задание 3
Выбери соответствующее древо испытаний вероятности
элементарного события P(НY)=qp.

13.

Задание 4
Вычисли вероятность элементарного события, в
котором вероятность успеха испытания p = 0,8, а перед
успехом случилось ровно 3 неуспеха
Задание 5
Кубик бросается до тех пор, пока не выпадет грань с
пятью очками.
Какая вероятность то, что пятёрка не выпадет никогда?

14.

Задание 6
Посчитай вероятность того, что будет сделано
ровно три броска в серии испытания по бросанию игральной
кости до тех пор, пока не выпадет тройка. Заполни пропуски в
решении. (Ответ в 1, 2 пункте запиши в виде несократимой
обыкновенной дроби, а в пункте 3 запиши десятичную дробь,
которую округли до тысячных.)

15.

Задание 7
Вероятность успеха в каждом отдельном испытании
равна p, вероятность неудачи равна q=1−p. Испытания
производятся последовательные, одинаковые и
независимые, пока не наступит успех.
Найдите вероятность события (выраженного
через p или q), если успех случится не позже третьего
испытания.

16.

Задание 8
Найди вероятность попадания в мишень, если до первого
попадания стрелок произведёт не
больше трёх выстрелов, а вероятность неуспеха при
каждом отдельном выстреле равна 0,5.
Задание 9
Простая вероятность серии испытаний равна 0,05,
простая вероятность серии этого же испытания, но с
другим количеством неудач,
равна 0,005. Посчитай вероятность того, что произойдёт
любое из данных двух испытаний.

17.

Задание 10
Найди вероятность, что Пётр, стреляя из лука, попадёт в
мишень на пятом выстреле из десяти попыток, если
вероятность попадания при одном выстреле равна 5/10.

18.

Домашнее задание
Задание № 1
Вероятность успеха в серии испытаний равна 0,93.
Найди вероятность неуспеха.
Задание № 2
Для экзамена необходимо повторить решение 70 типов
задач. Григорий успел повторить только 50. Найди
вероятность того, что Григорию придётся решать на
экзамене задачу, которую он не успел повторить.
(Ответ округли до сотых.)

19.

Домашнее задание
Задание № 3
Найди соответствующее древо испытаний вероятности
элементарного события P(ННY)=q2p.
Задание № 4
Вычисли вероятность элементарного события, в
котором вероятность успеха испытания p = 0,4, а перед
успехом случилось ровно 3 неуспеха

20.

Домашнее задание
Задание № 5
Вероятность успеха в каждом отдельном испытании
равна p, вероятность неудачи равна q=1−p. Испытания
производятся последовательные, одинаковые и
независимые, пока не наступит успех.
Отметь вероятность события (выраженного
через p или q), если успех случится позже пятого
испытания.