Похожие презентации:
Сложность алгоритма
1.
• Сложность задачиПо мере накопления опыта работы в той или иной области знаний человек
начинает интуитивно чувствовать, что одна задача более трудна, чем другая. Очень
часто задачу называют сложной из-за того, что она обладает разветвлённой
логической структурой, содержит большое количество проверок условий, переходов
и т. д. Программа, реализующая алгоритм её решения, также кажется нам сложной,
поскольку тяжело понять, что же она делает. А вот для компьютера выполнение
этой программы никакой трудности может не представлять! Потому что он просто
выполняет одну за другой команды, которые там написаны. Для него абсолютно
неважно, какие они именно – сложения или проверки условий и переходы.
Более сложной может показаться программа с текстом, состоящим из большего
числа операторов. Но и такой взгляд на сложность оказывается не вполне
оправданным. В самом деле, для компьютера две программы – состоящая из
одного оператора цикла, 100 раз повторяющего сложение двух чисел, и состоящая
из 100 операторов сложения, выписанных подряд, – практически одинаковы.
входных данных.
2.
• Сложность в теорииалгоритмов
Практическое использования алгоритмов показало, что огромное
значение имеет ещё одно их свойство – эффективность. Алгоритм должны быть
такими, чтобы исполнитель (компьютер) был способен выполнить его с
использованием имеющихся вычислительных ресурсов (скорость выполнения
операций и используемый объем памяти). Поэтому в теории алгоритмов сложность
– понятие, характеризующее количественно средства, необходимые для
реализации вычислимых функций. Принято различать сложность алгоритмов и
сложность вычислений.
Сложность алгоритма есть величина, характеризующая размеры его
записи в рассматриваемом алгоритмическом языке.
Сложность вычислений оценивается с помощью сигнализирующих
функций, определяющих время работы алгоритма или объем памяти, используемой
алгоритмом в процессе вычислений в зависимости от исходных данных.
3.
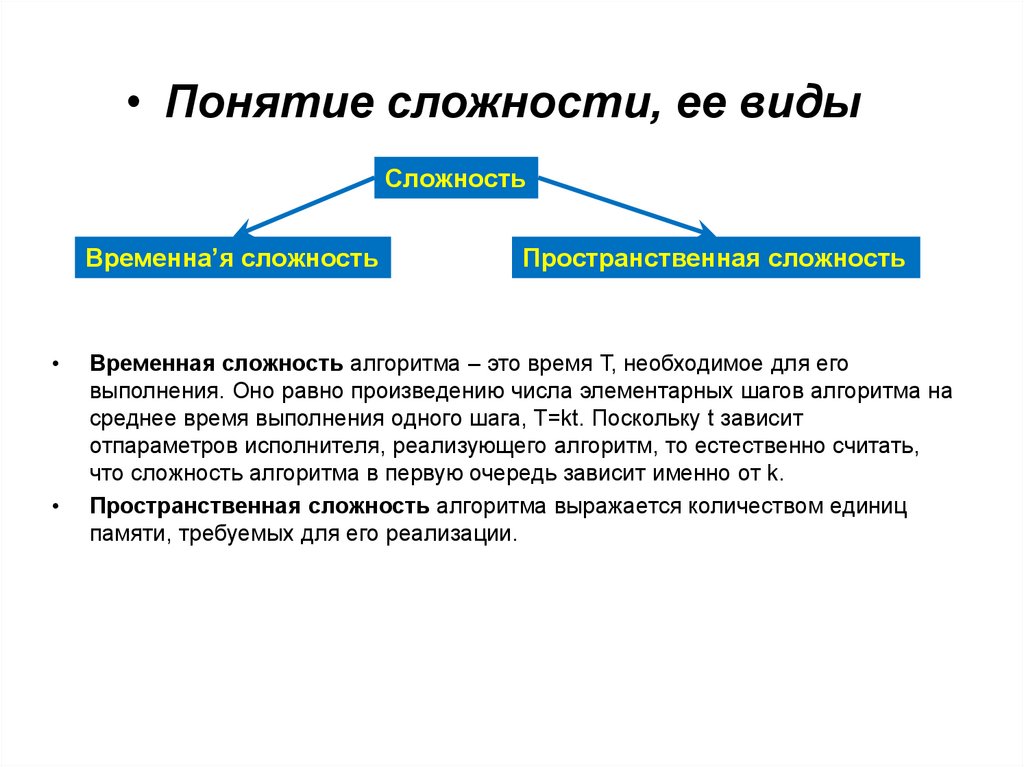
• Понятие сложности, ее видыСложность
Временна’я сложность
Пространственная сложность
Временная сложность алгоритма – это время Т, необходимое для его
выполнения. Оно равно произведению числа элементарных шагов алгоритма на
среднее время выполнения одного шага, T=kt. Поскольку t зависит
отпараметров исполнителя, реализующего алгоритм, то естественно считать,
что сложность алгоритма в первую очередь зависит именно от k.
Пространственная сложность алгоритма выражается количеством единиц
памяти, требуемых для его реализации.
4.
Оценка сложности алгоритмовПространственная сложность
Временная сложность
Многие алгоритмы предлагают выбор между объёмом памяти и скоростью.
5.
1.2. Оценка временной сложности1 с на 1000 чисел
10 с на миллион чисел
2 с на 1000 чисел
5 с на миллион чисел
Часто нельзя однозначно сказать, какой алгоритм лучше.
В общем случае сложность алгоритма можно оценить по порядку величины.
Говорят, что алгоритм имеет сложность O(f(n)), если при увеличении
размерности входных данных N, время выполнения алгоритма возрастает с
той же скоростью, что и функция f(N).
6.
• Оценка временной сложностиПространственная сложность не может расти быстрее временной, т.к. на
использование каждой дополнительной единицы памяти обязательно потребуется
дополнительное время. Поэтому для простоты часто ограничиваются
рассмотрением лишь временной сложности. На практике сложность алгоритма
обычно связывают с основным его параметром, существенно влияющим на
количество выполняемых действий. Как правило, это размер массива
обрабатываемых данных (размер задачи). Например, в задаче умножения двух
квадратных матриц это их порядок, в задаче упорядочивания массива – его
размерность. Сложность алгоритма (число операций, необходимых для его
реализации) выражают в виде функции от объема данных О (О большое).
7.
Поскольку производительность алгоритма может отличаться при входаходного и того же размера, обычно используется временная сложность
наихудшего случая (T(N))поведения алгоритма, которая определяется как
максимальное время, которое требуется для любого входа длины n.
Max:=A[1];
for J:=1 to N do
if A[J]>Max then
Max:=A[J]
Writeln(Max);
A={10, 9, 3, 5, 8, 4, 7, 6}
A={3, 4, 5, 6, 7, 8, 9, 10}
В приведенном алгоритме переменная J меняется от 1 до N. При
увеличении N вдвое в наихудшем случае количество тактов алгоритма
тоже увеличивается примерно в 2 раза. Скорость алгоритма линейно
зависит от N. Это определяет сложность алгоритма O(N).
8.
Max:=A[1,1];for I:=1 to N do
for J:=1 to N do
if A[I,J]>Max then
Max:=A[I,J]
Writeln(Max);
В приведенном алгоритме переменная J меняется от 1 до N. И этот цикл
повторяется N раз при различных значениях I, При увеличении N вдвое в
наихудшем случае количество тактов алгоритма тоже увеличивается
примерно в 4 раза. Скорость алгоритма зависит от N2. Это определяет
сложность алгоритма O(N2).
9.
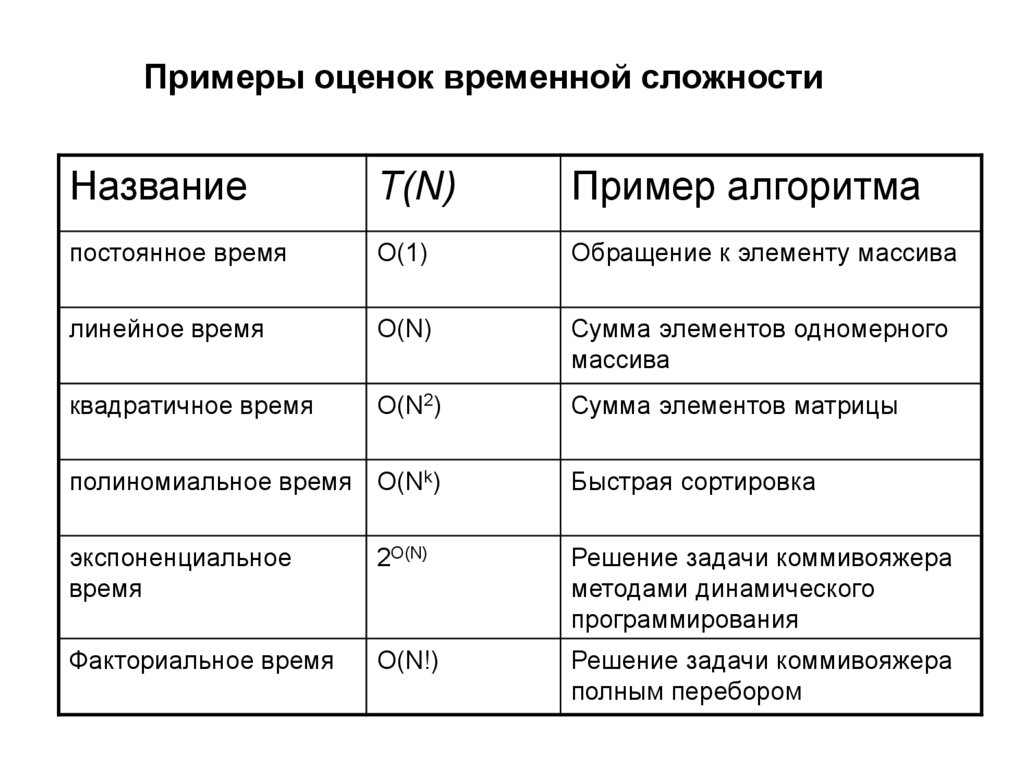
Примеры оценок временной сложностиНазвание
T(N)
Пример алгоритма
постоянное время
О(1)
Обращение к элементу массива
линейное время
O(N)
Сумма элементов одномерного
массива
квадратичное время
O(N2)
Сумма элементов матрицы
полиномиальное время O(Nk)
Быстрая сортировка
экспоненциальное
время
2O(N)
Решение задачи коммивояжера
методами динамического
программирования
Факториальное время
O(N!)
Решение задачи коммивояжера
полным перебором
10.
Классы временной сложностиКонцепция полиномиального времени приводит к нескольким классам
сложности в теории сложности вычислений.
P: Класс сложности задач разрешимости (КСЗР), которые могут быть решены
в детерминированной машине Тьюринга (МТ) за полиномиальное время.
NP: КСЗР, которые могут быть решены в недетерминированной МТ за
полиномиальное время.
ZPP: КСЗР, которые могут быть решены с нулевой ошибкой в вероятностной
МТ за полиномиальное время.
RP: КСЗР, которые могут быть решены с односторонними ошибками
в вероятностной МТ за полиномиальное время.
BPP: КСЗР, которые могут быть решены с двусторонними ошибками
в вероятностной МТ за полиномиальное время.
BQP: КСЗР, которые могут быть решены с двусторонними ошибками
в квантовой МТ за полиномиальное время.








 Информатика
Информатика








