Лекция 3. МАИ

1.

Лекция 3. Методы принятия
решений
Лекция №3 по дисциплине
Красноярск, 2024
1

2.

Системы поддержки принятия решений (СППР)
1
Сбор данных
2
Моделирование и анализ
3
Обоснованные решения
СППР собирает и интегрирует актуальные данные из различных источников для
поддержки принятия решений.
СППР использует передовую аналитику и методы моделирования для получения
информации и оценки различных сценариев.
СППР предоставляет менеджерам конкретные рекомендации для
информированного принятия стратегических решений.
2

3.

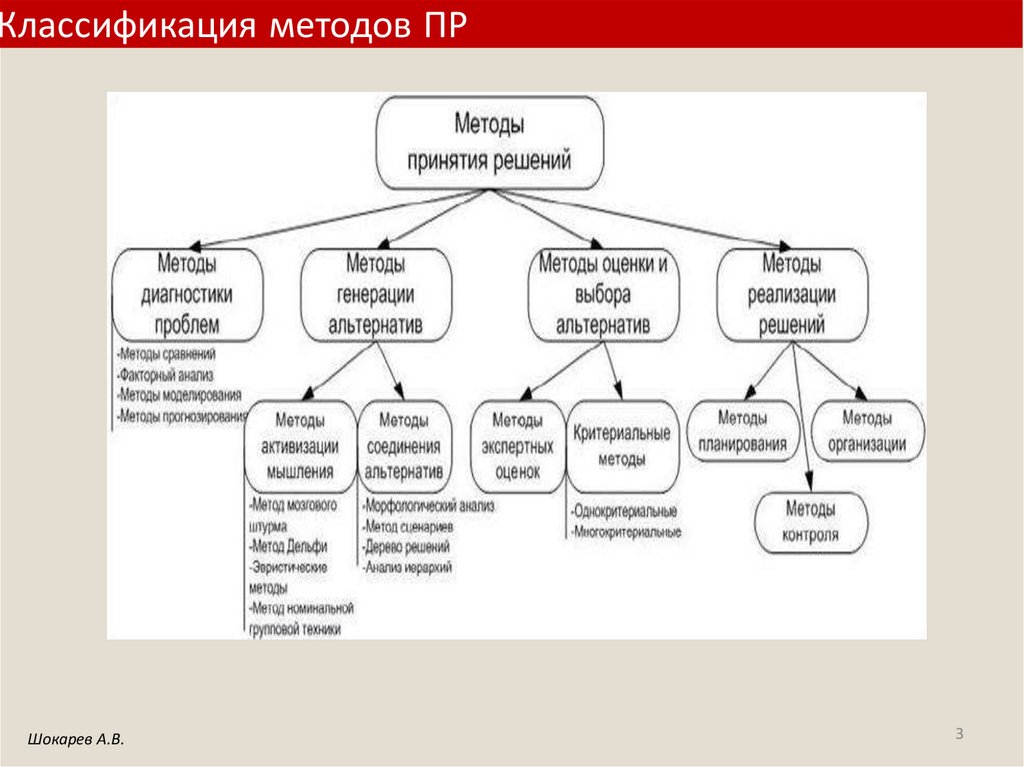
Классификация методов ПР
Шокарев А.В.
3

4.

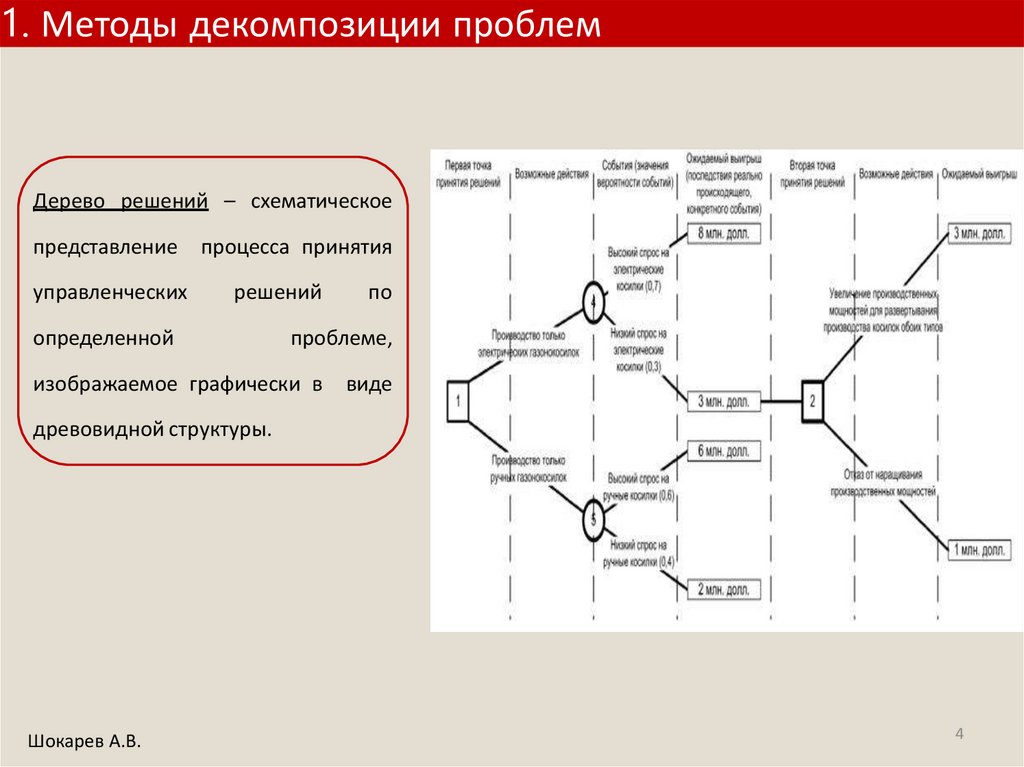
1. Методы декомпозиции проблем
Дерево решений – схематическое
представление
управленческих
процесса принятия
решений
определенной
по
проблеме,
изображаемое графически в
виде
древовидной структуры.
Шокарев А.В.
4

5.

2. Методы выявления альтернатив
1. Метод мозгового штурма
2. Метод Дельфи
3. Эвристические методы
4. Методы морфологического анализа
5. Метод синектики
6. Методы коллективных ассоциаций
5

6.

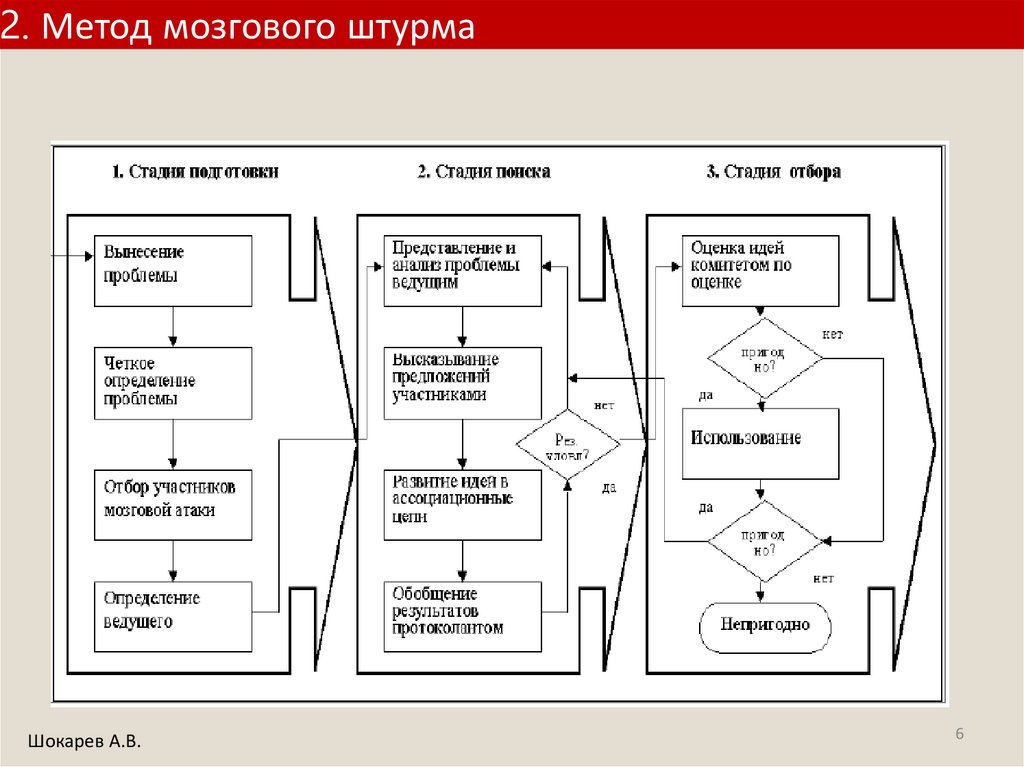
2. Метод мозгового штурма
Шокарев А.В.
6

7.

2. Метод Дельфи
Цель метода заключается в том, чтобы
получить согласованную информацию
высокой степени достоверности от
группы экспертов.
В нем реализована попытка устранить
противоречие,
возникающее
при
организации работы группы экспертов.
Суть его заключается в том, что если
опрашивать экспертов независимо друг
от друга, то возможны отклонения в
больших пределах. А если позволить
экспертам
взаимодействовать,
обмениваться мнениями в процессе
работы, то это может привести к
появлению
оценок,
навязанных
авторитетными коллегами.
Шокарев А.В.
7

8.

2. Эвристические методы
Эвристика – наука, изучающая продуктивное творческое мышление
(эвристическая деятельность). Эвристические методы – специальные
методы, используемые в процессе открытия нового. Эвристики – это
основанные на опыте: правила, стратегии, удачные приемы, упрощения или
иные средства, существенно ограничивающие пространство поиска
решения в сложных задачах.
Эвристические методы основаны на эффектах «озарения» и синергии,
типичные условия применения данных методов состоят в следующем:
дефицит времени на обоснование проблемной ситуации, перегруженность
информацией, затрудняющей процесс ее обработки.
Наиболее известные эвристики – эвристика доступности, эвристика
репрезентативности, эвристика привязки и согласования.
8

9.

2. Эвристические методы
1.
2.
3.
4.
5.
6.
7.
8.
конкретизация задачи;
обобщение
формулирование обратной задачи;
включение в другую структуру;
критика очевидных решений;
поиск привнесенных условий;
движение от конца к началу;
сближение данных и цели, перекодирование текста в
модель;
9. использование сходных задач;
10. рассмотрение с различных сторон;
11. анализ условий;
12. анализ конфликта;
13. выдвижение любых идей;
14. переструктурирование.
9

10.

2. Методы морфологич. анализа
Метод основан на комбинировании выделенных элементов или их признаков в
процессе поиска решения проблем. В рамках этого метода определяются все
возможные элементы, от которых может зависеть решение проблемы,
перечисляются возможные значения этих элементов, а затем наступает процесс
генерирования альтернатив путем перебора всех возможных сочетаний этих
значений.
При использовании данного метода исследования объект необходимо разбить на
функциональные части (функционально-морфологические признаки), такие, без
которых объект не будет выполнять свои функции. Затем следует выписать отдельно
морфологические признаки и записать информацию о них (варианты
осуществления) без связи с объектом (изделием), т.е. применить морфологические
признаки к другим аналогичным изделиям. Анализ полученных вариантов выявляет
такие их комбинации, которые при обычном переборе могут быть упущены.
10

11.

3. Методы выбора альт.-в в условиях определенности
Линейное
1.
2.
3.
4.
5.
6.
7.
программирование
задачи о распределении ограниченных ресурсов (задачи
оптимального планирования);
задачи об оптимальной корзине продуктов (задачи о диете, задачи
оптимального смешения);
задачи оптимального раскроя (материалов, заготовок);
транспортные задачи;
задачи о назначениях;
задачи оптимизации финансовых потоков;
задачи оптимизации графиков платежей.
11

12.

3. Методы выбора альтернатив в условиях риска
Для предоставления и анализа
результатов
выбранных
альтернативных
стратегий
используют матрицу
решений,
называемую
также
платежной
матрицей.
A1, A2, A3 –альтернативные стратегии
действий;
S1, S2, S3 – состояние экономики
(стабильность, спад, рост и др.);
E11; E12; E13; E21; … E33; … – результаты
решений.
Числа
в
ячейках
матрицы
представляют
собой результаты
реализации Eij стратегии Ai в
условиях Sj. При этом в условиях
риска вероятность наступления Sj
известна – wj(Sj).
Шокарев А.В.
12

13.

3. Методы выбора альтернатив в условиях риска
Методы принятия решений в условиях риска используют теорию выбора,
получившую название теории полезности. В соответствии с этой теорией ЛПР
выбирает Ai из совокупности {Ai} (i = 1 … n), которая максимизирует ожидаемую
стоимость его функции полезности Ej.
В условиях риска при принятии решения основным моментом является
определение вероятности наступления состояния среды Sj , т. е. степени риска.
После определения вероятности wj(Sj) наступления состояния среды Sj,
определяют ожидаемую стоимость реализации каждой альтернативы, которая
представляет собой средневзвешенную стоимость E(Ai):
где E(Ai) – результат реализации Ai; wj(Sj) – вероятность наступления Sj.
Оптимальной стратегией является та, которая обеспечивает наибольшую
ожидаемую стоимость:
13

14.

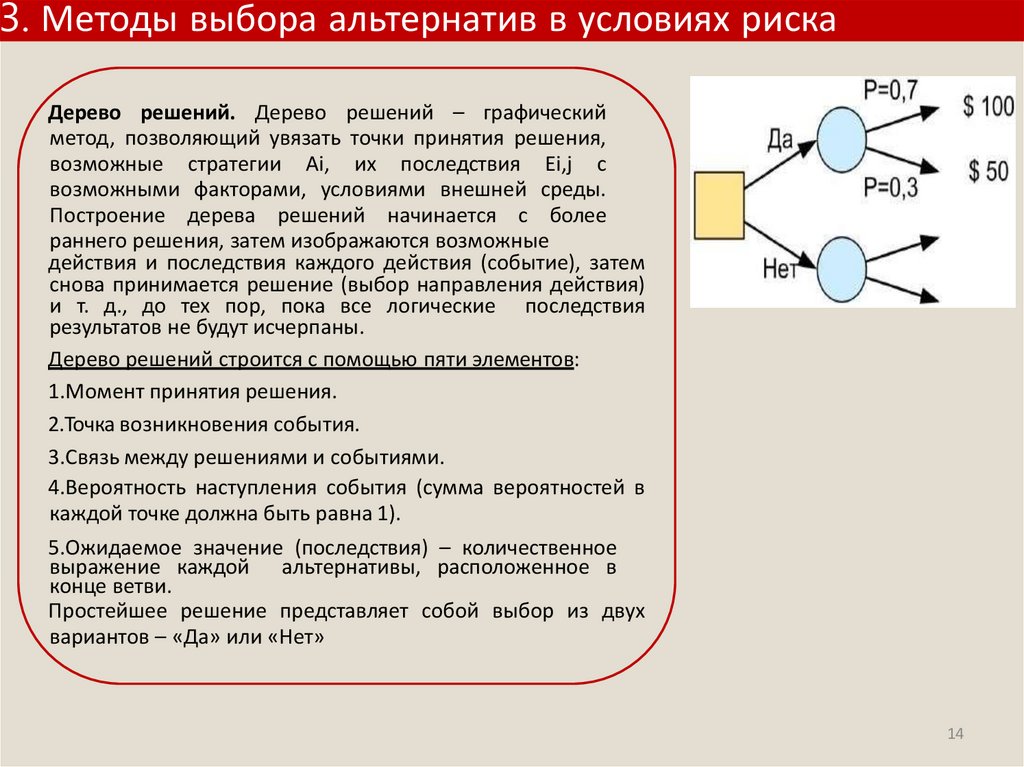
3. Методы выбора альтернатив в условиях риска
Дерево решений. Дерево решений – графический
метод, позволяющий увязать точки принятия решения,
возможные стратегии Ai, их последствия Ei,j с
возможными факторами, условиями внешней среды.
Построение дерева решений начинается с более
раннего решения, затем изображаются возможные
действия и последствия каждого действия (событие), затем
снова принимается решение (выбор направления действия)
и т. д., до тех пор, пока все логические последствия
результатов не будут исчерпаны.
Дерево решений строится с помощью пяти элементов:
1.Момент принятия решения.
2.Точка возникновения события.
3.Связь между решениями и событиями.
4.Вероятность наступления события (сумма вероятностей в
каждой точке должна быть равна 1).
5.Ожидаемое значение (последствия) – количественное
выражение каждой альтернативы, расположенное в
конце ветви.
Простейшее решение представляет собой выбор из двух
вариантов – «Да» или «Нет»
14

15.

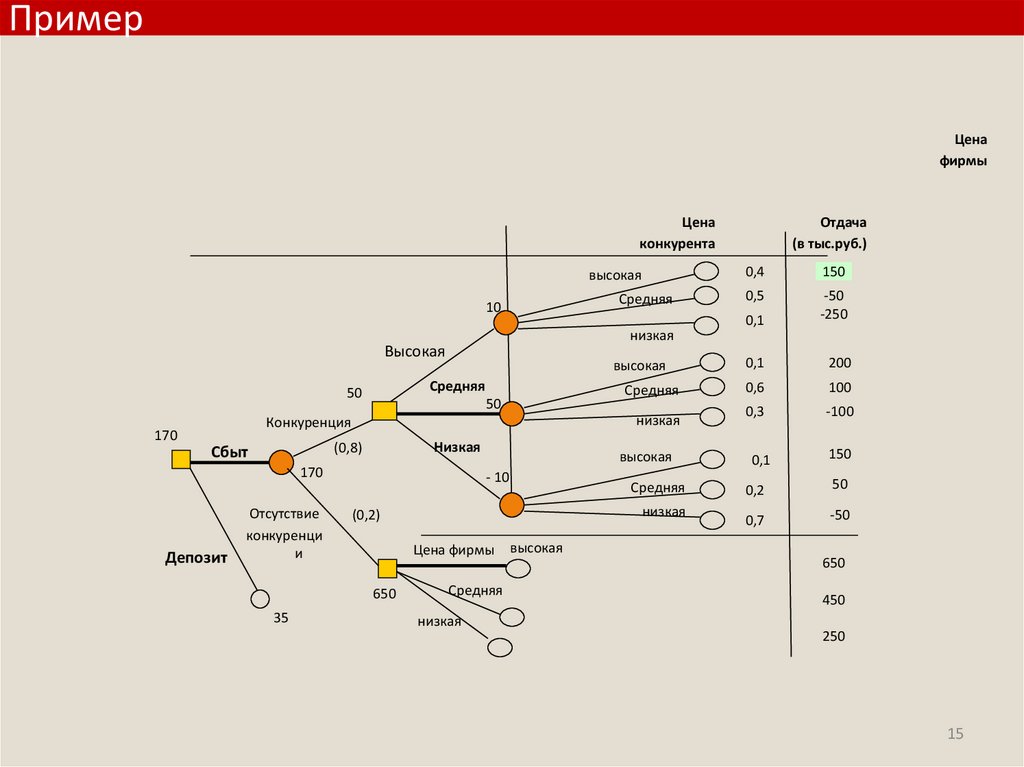
Пример
Цена
фирмы
Цена
конкурента
высокая
Средняя
10
высокая
Средняя
Средняя
50
низкая
Конкуренция
170
Низкая
(0,8)
Сбыт
170
Депозит
Отсутствие
конкуренци
и
35
высокая
- 10
Средняя
низкая
(0,2)
Цена фирмы
650
0,4
150
0,5
0,1
-50
-250
0,1
200
0,6
100
0,3
-100
0,1
150
0,2
50
0,7
-50
низкая
Высокая
50
Отдача
(в тыс.руб.)
Средняя
высокая
650
450
низкая
250
15

16.

Пример
Дерево «выстраивается» слева направо.
Ветви, исходящие из квадратных узлов,
обозначают альтернативы; ветви, исходящие из
круглых узлов, — возможные события (т.е.
возможные условия).
После того как дерево решения построено, оно
анализируется справа налево, т.е. начинать надо
с последнего принятого решения.
Для каждого решения выбирается альтернатива с
наибольшим показателем отдачи (или с
наименьшими затратами).
Если за принятием решения следует несколько
возможных вариантов событий, выбирают
альтернативу с наибольшей предполагаемой
прибылью (или с наименьшей предполагаемой
величиной затрат).
16

17.

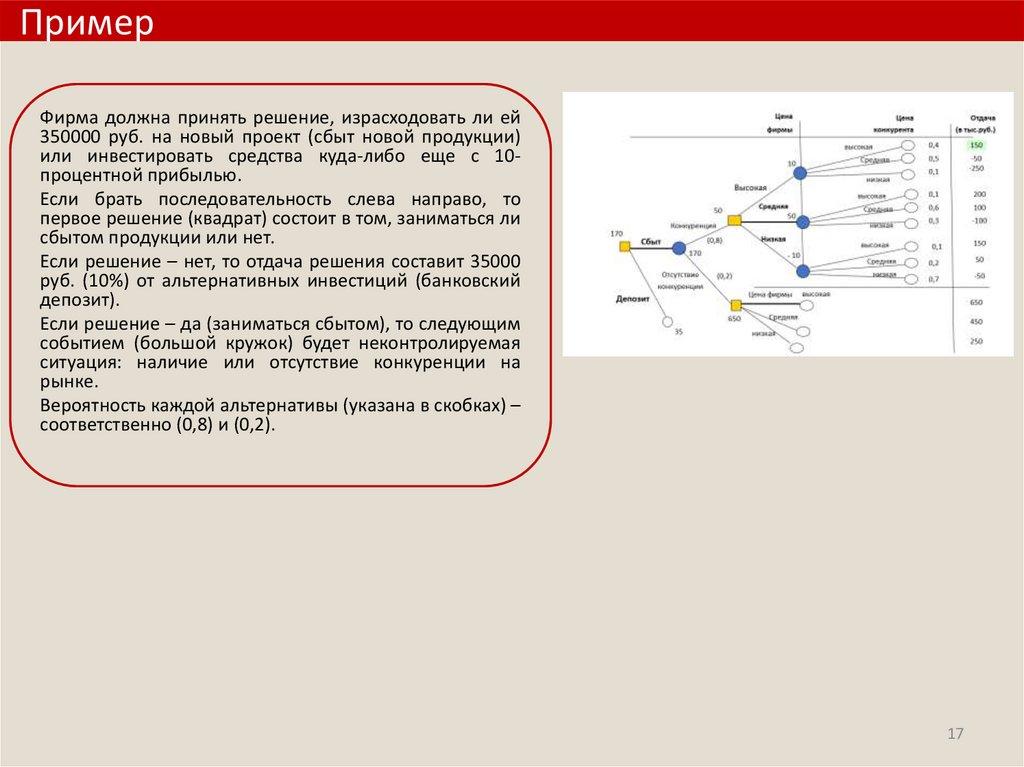
Пример
Фирма должна принять решение, израсходовать ли ей
350000 руб. на новый проект (сбыт новой продукции)
или инвестировать средства куда-либо еще с 10процентной прибылью.
Если брать последовательность слева направо, то
первое решение (квадрат) состоит в том, заниматься ли
сбытом продукции или нет.
Если решение – нет, то отдача решения составит 35000
руб. (10%) от альтернативных инвестиций (банковский
депозит).
Если решение – да (заниматься сбытом), то следующим
событием (большой кружок) будет неконтролируемая
ситуация: наличие или отсутствие конкуренции на
рынке.
Вероятность каждой альтернативы (указана в скобках) –
соответственно (0,8) и (0,2).
17

18.

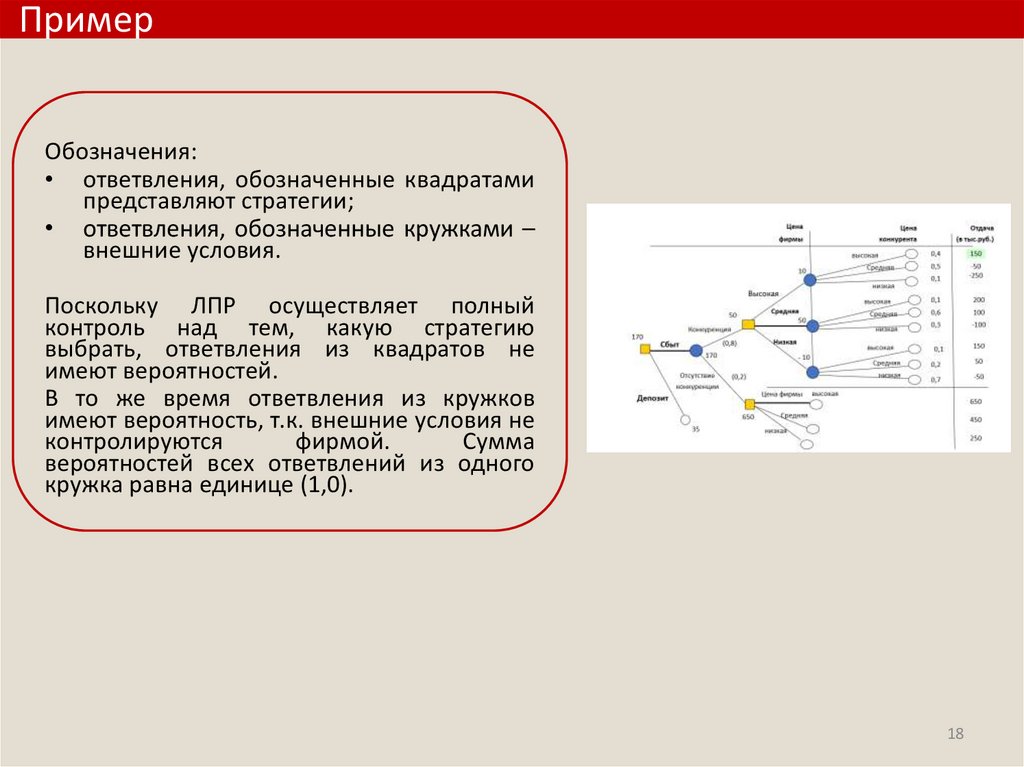
Пример
Обозначения:
• ответвления, обозначенные квадратами
представляют стратегии;
• ответвления, обозначенные кружками –
внешние условия.
Поскольку ЛПР осуществляет полный
контроль над тем, какую стратегию
выбрать, ответвления из квадратов не
имеют вероятностей.
В то же время ответвления из кружков
имеют вероятность, т.к. внешние условия не
контролируются
фирмой.
Сумма
вероятностей всех ответвлений из одного
кружка равна единице (1,0).
18

19.

Пример
Если конкуренция отсутствует, то единственное
оставшееся решение должно состоять в
следующем: какую назначить цену за продукцию:
(высокую, среднюю или низкую).
Эти три ответвления имеют каждое – свою отдачу
(обозначены в конце ответвления: 650тыс.руб.,
450 и 250 тыс.руб.).
Далее каждое ответвление вновь подразделяется
на три, обозначая
намерения конкурента
назначить высокую, среднюю или низкую цену.
Дерево решения представляет графическую
форму ожидания того, что цена, которую
назначит конкурент, будет зависеть от цены,
которую устанавливает фирма.
А последующая прибыль фирмы зависит от того,
какую цену назначит конкурент.
19

20.

Пример
Поскольку каждое решение зависит от оценки событий,
которые будут происходить позднее, анализ дерева решения
начинается с конца последовательности и продвигается в
обратном направлении.
Начиная с верхней правой части рисунка , вычисляем
предполагаемую стоимость варианта, если цена фирмы
высокая и если имеет место конкуренция:
(150*0,4) + (-50*0,5) + (-250*0,1) = 10
Аналогично исчисляется предполагаемая стоимость средней
и низкой цены.
Выбирается альтернатива с наибольшей стоимостью:
50 тыс.руб. – соответствует альтернативе со средней ценой.
При альтернативном состоянии отсутствия конкуренции
(нижнее ответвление) назначаем высокую цену.
Теперь находим предполагаемую стоимость для первого
события: (50*0,8)+(650*0,2)=170 тыс.руб.
Теперь фирма готова принять решение: выбрать проект
связанный с реализацией товаров.
20

21.

3. Методы выбора альтернатив в условиях неопределенности
Выбор наилучшего решения в условиях неопределенности существенно
зависит от того, какова степень этой неопределенности, т.е. от того, какой
информацией располагает ЛПР. Практикуются два основных подхода к
принятию решения в условиях неопределенности.
Если степень неопределенности слишком высока, то ЛПР предпочитает не
делать допущений относительно вероятностей различных внешних условий,
т.е. это лицо может или не учитывать вероятности, или рассматривать их как
равные, что практически одно и то же. Если применяется данный подход, то
для оценки предполагаемых стратегий имеются четыре критерия решения:
а) критерий решения Вальда, называемый также максимином;
б) альфа-критерий решения Гурвица;
в) критерий решений Сэвиджа, называемый также критерием отказа от
минимакса;
г) критерий решений Лапласа, называемый также критерием решения Бэйеса.
21

22.

3. Методы выбора альтернатив в условиях неопределенности
Критерий решения Вальда. Критерием Вальда «рассчитывай на худшее» (критерий
крайнего пессимизма или макси-мин) называют критерий, предписывающий
обеспечить значение параметра эффекта равного аi,
Этот критерий ориентирует лицо, принимающее решение, на наихудшие условия и
рекомендует выбрать ту стратегию, для которой выигрыш максимален. В других, более
благоприятных условиях использование
этого критерия приводит к потере
эффективности системы или операции.
Альфа-критерий решения Гурвица. Этот критерий рекомендует при выборе решения в
условиях неопределенности не руководствоваться ни крайним пессимизмом (всегда
«рассчитывай на худшее», a=0), ни крайним оптимизмом («все будет наилучшим
образом», a=1). Рекомендуется некое среднее решение (0≤a≤1). Этот критерий имеет
вид
где a – некий коэффициент, выбираемый экспериментально из интервала между 0 и 1.
Использование этого коэффициента вносит дополнительный субъективизм в принятие
решений с использованием критерия Гурвица.
22

23.

3. Методы выбора альтернатив в условиях неопределенности
Критерий решения Сэвиджа. Минимаксный критерий Сэвиджа. В соответствии с этим критерием,
если требуется в любых условиях избежать большого риска, то оптимальным будет то решение, для
которого риск, максимальный при различных вариантах условий, окажется минимальным.
Критерий минимаксного риска Сэвиджа. При его использовании обеспечивается наименьшее
значение максимальной величины риска:
где риск rij определяется выражением: rij = bj - eij, b – максимально возможный выигрыш.
Критерий Сэвиджа, как и критерий Вальда, – это критерий крайнего пессимизма, но только
пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше, по
сравнению с тем, чего можно было бы достичь в данных условиях.
Критерий решения Лапласа. Критерий Лапласа, или Байесов критерий гласит, что если
вероятности состояния среды неизвестны, то они должны приниматься как равные. В этом случае
выбирается стратегия, характеризующаяся самой предполагаемой стоимостью при условии равных
вероятностей. Критерий Лапласа позволяет условие неопределенности сводить к условиям риска.
Критерий Лапласа называют критерием рациональности, и он подходит для стратегических
долгосрочных решений, как и все вышеназванные критерии.
Кроме вышеназванных четырех критериев, для принятия решений в условиях неопределенности
существуют неколичественные методы, такие как приобретение дополнительной информации,
хеджирование, гибкое инвестирование и др.
23

24.

• Предприятие может выпускать 3 вида продукции А1,
А2 и А3, получая при этом прибыль, зависящую от
спроса, который может быть в одном из 4-х состояний
(В1, В2, В3, В4). Элементы платежной матрицы
характеризуют прибыль, которую получат при выпуске
i-й продукции при j-м состоянии спроса. Игра
предприятия А против спроса В задана платежной
матрицей:
• В1 В2
• А1 2
• А2 2
• А3 4
В3
7
8
3
В4
8
7
4
https://math.semestr.ru/games/stat.php
6
3
2
24

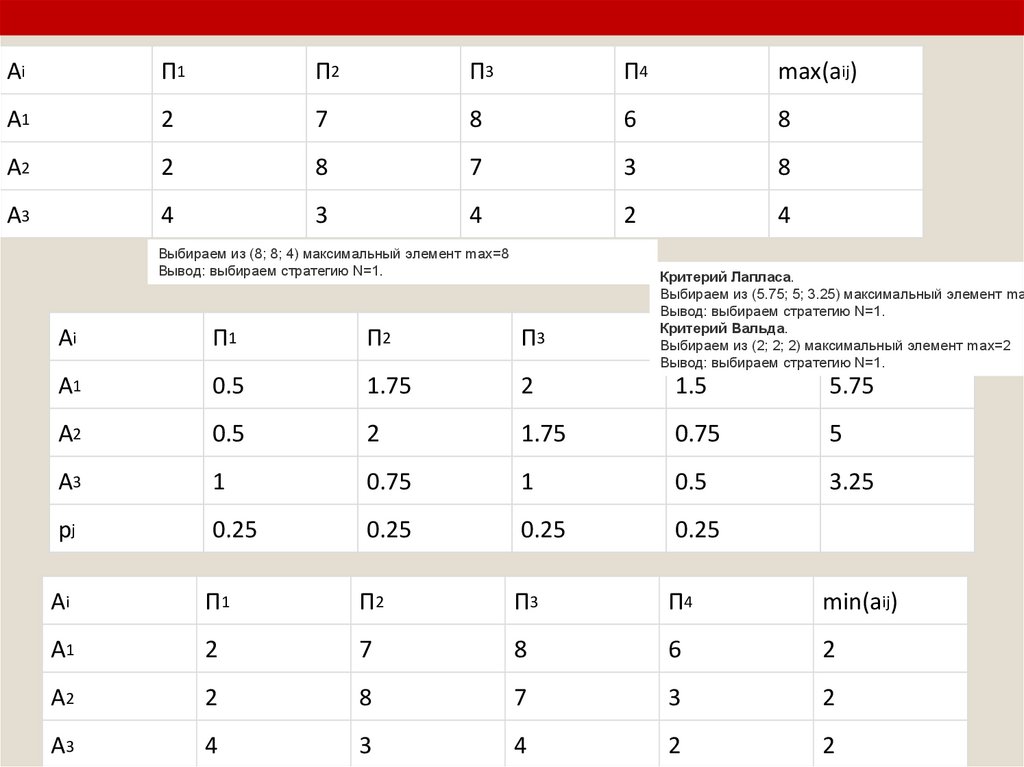
25.

Ai
П1
П2
П3
П4
max(aij)
A1
2
7
8
6
8
A2
2
8
7
3
8
A3
4
3
4
2
4
Выбираем из (8; 8; 4) максимальный элемент max=8
Вывод: выбираем стратегию N=1.
Ai
П1
П2
П3
A1
0.5
1.75
A2
0.5
A3
Критерий Лапласа.
Выбираем из (5.75; 5; 3.25) максимальный элемент ma
Вывод: выбираем стратегию N=1.
Критерий Вальда.
4
ij
Выбираем
из (2; 2; 2) максимальный
элемент max=2
Вывод: выбираем стратегию N=1.
П
∑(a )
2
1.5
5.75
2
1.75
0.75
5
1
0.75
1
0.5
3.25
pj
0.25
0.25
0.25
0.25
Ai
П1
П2
П3
П4
min(aij)
A1
2
7
8
6
2
A2
2
8
7
3
2
A3
4
3
4
2
2
25

26.

Ai
П1
П2
П3
П4
max(aij)
A1
2
1
0
0
2
A2
2
0
1
3
3
A3
0
5
4
4
5
Ai
П1
П2
П3
П4
A1
2
1
0
0
A2
2
0
1
3
A3
0
5
4
4
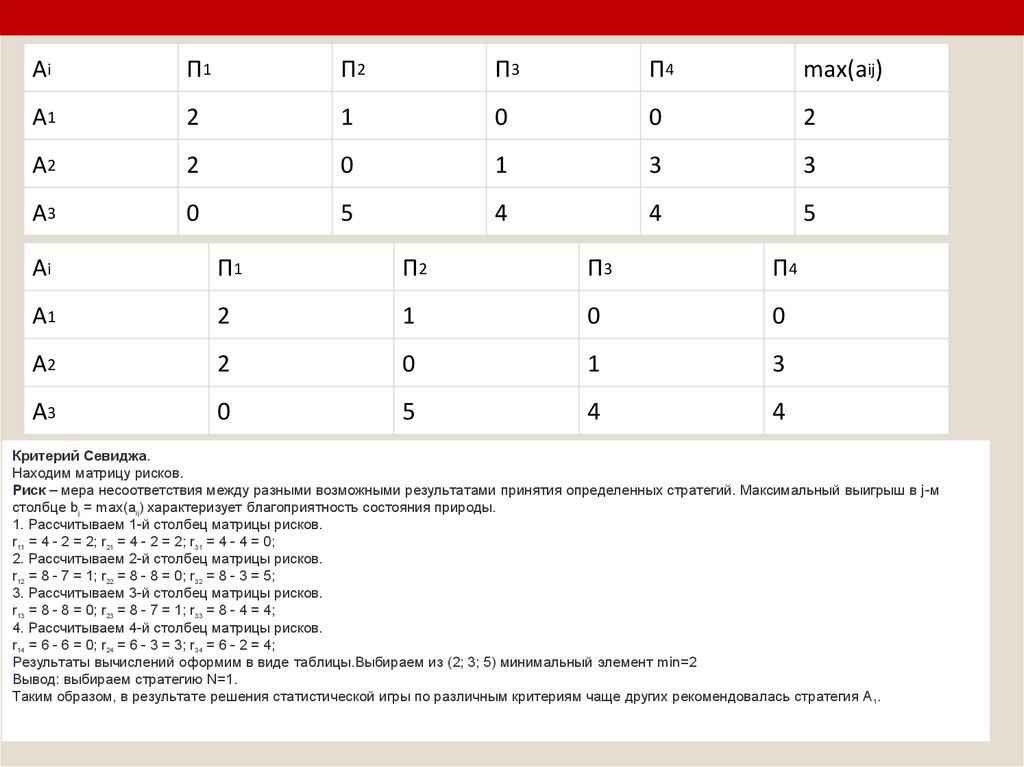
Критерий Севиджа.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м
столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 4 - 2 = 2; r21 = 4 - 2 = 2; r31 = 4 - 4 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 8 - 7 = 1; r22 = 8 - 8 = 0; r32 = 8 - 3 = 5;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 8 - 8 = 0; r23 = 8 - 7 = 1; r33 = 8 - 4 = 4;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 6 - 6 = 0; r24 = 6 - 3 = 3; r34 = 6 - 2 = 4;
Результаты вычислений оформим в виде таблицы.Выбираем из (2; 3; 5) минимальный элемент min=2
Вывод: выбираем стратегию N=1.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A 1.
26

27.

3. Экспертные методы
Экспертные оценки – это качественные оценки, основанные на информации
неколичественного (качественного) характера, которые могут быть получены только с
помощью специалистов – экспертов. Эксперт – это высококвалифицированный специалист,
полагающийся на свои знания, опыт, интуицию и умение оценивать сложные факторы
(явления) и способный создать собственную обоснованную (интуитивную) модель
анализируемого явления (проблемы), если он располагает необходимой для этого исходной
информацией.
Сущность метода экспертных оценок заключается в логико-интуитивном анализе
внутренней и внешней среды организации, разработке альтернатив и количественной оценке
их качества. Обобщенное мнение экспертов служит основанием для осуществления выбора.
Методом экспертного оценивания решаются следующие типовые задачи:
• определение состава возможных событий в какой-либо системе в определенном
интервале времени;
• определение вероятностей событий и временных интервалов во множестве событий;
• структурирование проблемного поля организации и определение приоритетности
решения проблем;
• дифференциация целей управления до задач и определение приоритетности их решения;
• генерирование альтернатив;
• фильтрация множества альтернатив и оценка их предпочтительности.
27

28.

3. Экспертные методы
Экспертные суждения – содержательные высказывания (определяющие
состав, структуру, функциональность исследуемой системы, сущностей и их
атрибутов), количественная или качественная оценка какой- либо сущности
(т.е. определение количественных и качественных атрибутов и их значений).
Экспертное ранжирование. Ранжирование применяется в случаях, когда
невозможна или нецелесообразна непосредственная оценка. При этом
ранжирование объектов содержит лишь информацию о том, какой из них
более предпочтителен, и не содержит информации о том, насколько или
во сколько раз один объект предпочтительнее другого.
Ранг – степень отличия по какому-либо признаку, а ранжирование –
процесс определения рангов, относительных количественных оценок
степеней отличий по качественным признакам.
28

29.

3. Экспертные методы
1.
Метод простой ранжировки. Заключается в том, что эксперты располагают
объекты ранжирования (например, критерии) в порядке убывания их
значимости (скажем, для альтернатив это убывание предпочтительности).
Ранги обозначаются цифрами от 1 до n, где n – количество рангов. Сумма
рангов Sn при этом будет равна сумме чисел натурального ряда:
2.
Метод непосредственной оценки заключается в отнесении объекта оценки
к определенному значению по оценочной шкале (т.е. в присвоении объекту
оценки балла в определенном интервале), например, от 0 до 10 – в
соответствии с предпочтением по какому-либо признаку или их группе
(альтернативы, например, по предпочтению; критерии – по значимости;
факторы внешней среды – по оказываемому влиянию; проблемы – по
приоритетности решения).
29

30.

3. Экспертные методы
Метод парных сравнений заключается в определении предпочтений элементов, расположенных в
левом столбце, над элементами, расположенными в верхней строке. При этом составляется матрица,
по строкам и столбцам которой располагают сравниваемые объекты
Матрица парных сравнений для четырех объектов
В ячейке А1,2 вписана единица, это означает, что элемент А1 получает большую оценку, чем
элемент А2. Соответственно в ячейке А2,1 пишут 0, а в ячейке А1,4 вписана 1, и затем, суммируя
значения по строкам, получают ранги объектов.
Шокарев А.В.
30

31.

Условия
Условиями, предопределяющими необходимость применения экспертных
процедур, являются:
1. качественный характер исходной информации (отсутствие информации о
характеристиках объекта исследования в количественной форме);
2. большая неопределенность исходных данных для проведения анализа
проблемы;
3. отсутствие математической формализации предмета оценки;
4. нецелесообразность, недостаток времени и средств для исследования
проблемы с применением формальных подходов;
5. отсутствие технических средств для моделирования проблемной ситуации.
31

32.

Экспертный анализ
Всю совокупность методов экспертного анализа можно разделить:
• методы оценки (безкритериальные и критериальные);
• оценочно-поисковые методы.
В зависимости от числа участвующих в опросе экспертов методы экспертного
анализа подразделяются на:
• методы формирования индивидуальных экспертных оценок;
• методы формирования коллективных экспертных оценок.
Любой метод экспертного анализа представляет собой совокупность
процедур, направленных на получение информации эвристического
происхождения и обработку этой информации с помощью математикостатистических приемов.
32

33.

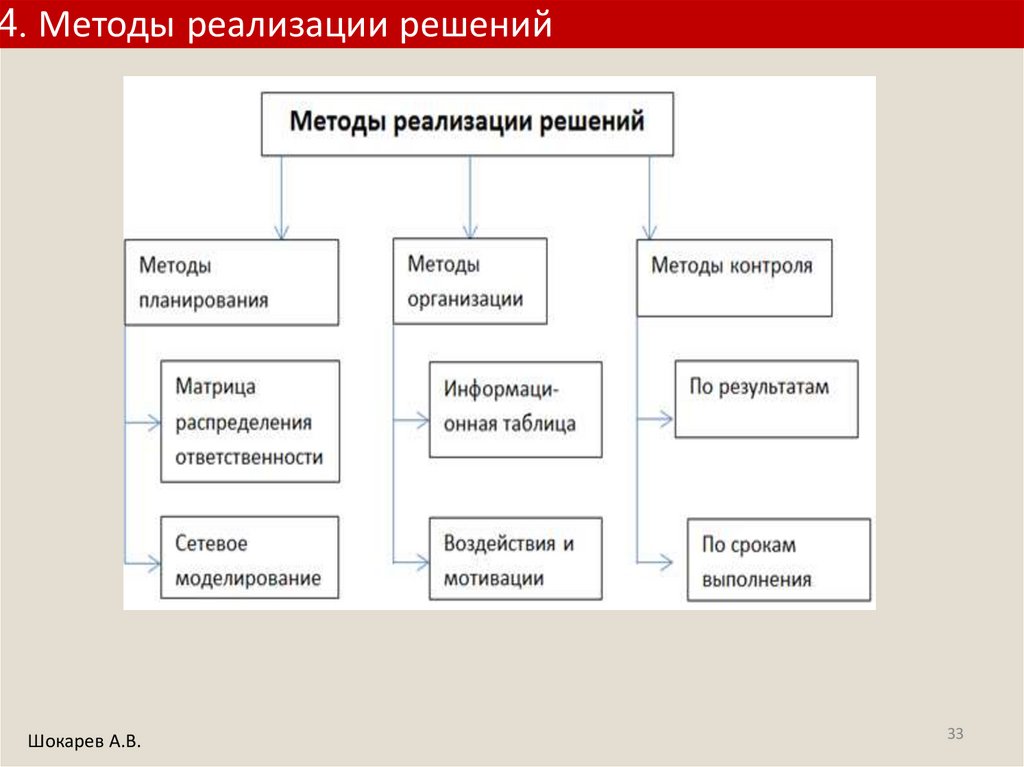
4. Методы реализации решений
Шокарев А.В.
33

34.

Теория игр
Теория игр изучает и рассматривает методы определения оптимального
поведения при управлении системами, в которых характерно наличие
конфликтной ситуации (столкновение интересов).
Участники конфликтов вынуждены действовать в условиях риска и
неопределенности
Модель конфликтной ситуации – игра, которая описывает:
а) множество заинтересованных сторон, которые называются игроками;
б) возможные действия каждой из сторон, именуемые стратегиями или
ходами;
в) интересы сторон, представленные функциями выигрыша (платежа) для
каждого из игроков.
34

35.

Основные определения
Выбор и осуществление одного из предусмотренных правилами действий
называется ходом игрока. Личный ход – это сознательный выбор игроком
одного из возможных действий. Случайный ход – это случайно выбранное
действие.
Стратегией игрока называется совокупность правил, определяющих выбор
действия при каждом ходе в зависимости от сложившейся ситуации.
Чтобы решить игру, следует для каждого игрока выбрать стратегию, которая
удовлетворяет условию оптимальности, то есть один из игроков получает
максимальный выигрыш, когда второй придерживается своей стратегии.
Второй игрок должен иметь минимальный проигрыш, если первый
придерживается своей стратегии.
Такие стратегии называются оптимальными.
Оптимальные стратегии должны удовлетворять условию устойчивости, то
есть любому из игроков должно быть невыгодно отказываться от своей
стратегии.
35

36.

Классификация
Игра называется парной, если в ней участвуют два игрока, и
множественной, если число игроков более двух.
Игра называется с нулевой суммой или антагонистической, если
выигрыш одного из игроков равен проигрышу другого. Игры с
постоянной разностью – игроки выигрывают и проигрывают
одновременно.
Игра называется конечной, если у каждого игрока имеется конечное
число стратегий, и бесконечной – в противном случае.
Бескоалиционными называются игры, в которых игроки не имеют права
вступать в соглашения. В коалиционной игре игроки могут вступать в
соглашения и образовывать коалиции.
В кооперативной игре игроки могут принимать соглашения о своих
стратегиях (возможность предварительных переговоров) до начала
игры. В некооперативной игре игроки не могут координировать свои
стратегии, принимают решения независимо друг от друга.
36

37.

Матричная и биматричная игра
Матричная – это конечная игра двух игроков с нулевой суммой, в
которой задаются выигрыши первого игрока в виде матрицы.
Любая матричная игра имеет решение и может быть реализована
методами линейного программирования.
Матричные игры еще называют играми в нормальной форме.
Биматричная игра – это конечная игра двух игроков с ненулевой
суммой, в которой есть матрицы выигрышей (проигрышей) отдельно для
каждого участника.
37

38.

Постановка задачи
Основной задачей теории игр является не описание, а разрешение
конфликтов, т.е. построение компромиссных взаимовыгодных решений,
которые полностью или хотя бы частично согласовывают интересы всех
взаимодействующих сторон.
Целью теории игр является выработка рекомендаций по разумному
поведению участников конфликта (определение оптимальных стратегий
поведения игроков).
Предметом изучения теории игр являются конфликтные ситуации.
38

39.

Теория стратегий
Чистая стратегия даёт полную определённость, каким образом игрок продолжит
игру. В частности, она определяет результат для каждого возможного выбора,
который игроку может придётся сделать.
Пространством стратегий называют множество всех чистых стратегий, доступных
данному игроку.
Смешанная стратегия является указанием вероятности каждой чистой стратегии.
Это означает, что игрок выбирает одну из чистых стратегий в соответствии с
вероятностями, заданными смешанной стратегией. Выбор осуществляется перед
началом каждой игры и не меняется до её конца.
Каждая чистая стратегия является частным случаем смешанной, когда
вероятность одной из чистых стратегий равна единице, а остальных возможных
чистых стратегий - нулю.
Стратегия, обеспечивающая при многократном повторении игры максимально
возможный средний выигрыш или минимально возможный средний проигрыш
данному игроку, независимо от стратегий, применяемых другими игроками,
называется оптимальной.
Набор стратегий - стратегии для каждого из игроков, которые полностью
описывают все действия в игре. Набор стратегий обязан включать одну и только
одну стратегию для каждого игрока
39

40.

Матричная игра
Матричная игра – это антогонистическая игра, которая задаётся
набором чистых стратегий {X1, …, Xn} и {Y1, …, Ym} первого и второго
игроков, а также платёжной матрицей (aij)nxm, определяющей выигрыш
первого игрока (или проигрыш второго игрока) при выборе игроками
чистых стратегий Xi и Yj соответственно.
• Цель первого игрока – максимизация своего выигрыша.
• Цель второго игрока – минимизация выигрыша противника.
40

41.

Р-ние матр. игр в чист. страт-ях
Принцип максимина
Предположим, что второй игрок заранее знает все ходы первого игрока. Тогда на каждую
стратегию Xi он отвечает наилучшей контрстратегией Yj(i), для которой aij(i) <= aij для всех j
=1,m. Оптимальной чистой стратегией первого игрока является стратегия Xp (максиминная
стратегия), для которой выполняется:
Величину называют нижней ценой игры в чистых стратегиях.
Принцип минимакса
Рассмотрим аналогичную ситуацию для первого игрока. Оптимальной чистой стратегией
второго игрока является стратегия Yq (минимаксная стратегия), для которой выполняется:
Величину называют верхней ценой игры в чистых стратегиях.
Нижняя цена игры не может быть больше верхней цены игры ( v ).
Цена игры в чистых стратегиях – значение выигрыша первого игрока при условии выбора
игроками их оптимальных чистых стратегий.
41

42.

Пример
Игра в «орлянку». Если оба выбирают одинаковые
стратегии (оба говорят “орел”), то 1-й выигрывает 1 рубль
(а второй проигрывает); если выбирают разные, то 2-й
выигрывает. Матрица выигрыша первого игрока (Н1)
Орел
Решка
Орел
1
–1
Решка
–1
1
Орел
Решка
Орел
–1
1
Решка
1
–1
Матрица выигрыша второго игрока (Н2)
42

43.

Пример
0,5 0,6 0,8
0,9 0,7 0,8
0,7 0,6 0,6
Платежная матрица игры
B1
B2
B3
α
A1
A2
A3
β
43

44.

Пример
0,5 0,6 0,8
0,9 0,7 0,8
0,7 0,6 0,6
Платежная матрица игры
B1
B2
B3
α
A1
0,5
0,6
0,8
0,5
A2
0,9
0,7
0,8
0,7
A3
0,7
0,6
0,6
0,6
β
0,9
0,7
0,8
0,7
0.7 – цена игры. Седловая точка (А2, В2).
44

45.

Смешанная стратегия
• Если игра не имеет седловой точки, то применение
чистых стратегий не дает оптимального решения игры.
• Смешанной стратегией называется применение чистых
стратегий
с
разными
вероятностями.
Сумма
вероятностей равна 1. Цена игры будет удовлетворять
неравенству:
• Каждая конечная игра имеет, по крайней мере, одно
оптимальное решение, возможно, среди смешанных
стратегий.
45

46.

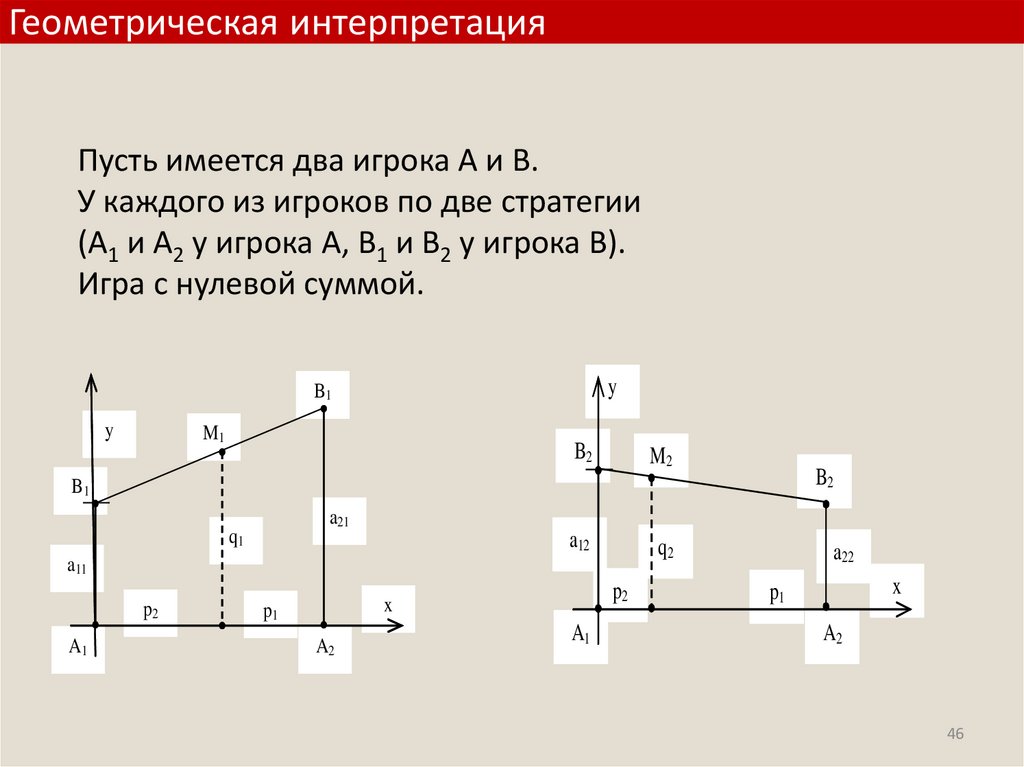
Геометрическая интерпретация
Пусть имеется два игрока А и В.
У каждого из игроков по две стратегии
(А1 и А2 у игрока А, В1 и В2 у игрока В).
Игра с нулевой суммой.
y
B1
y
M1
B2
M2
B2
B1
a21
q1
a12
q2
a11
p2
A1
p2
x
p1
A2
A1
a22
x
p1
A2
46

47.

Решение игры граф. способом
y
B1
B2
N
B2
B1
p2
A1
SA*
(p1*, p2* )
x
p1
A2
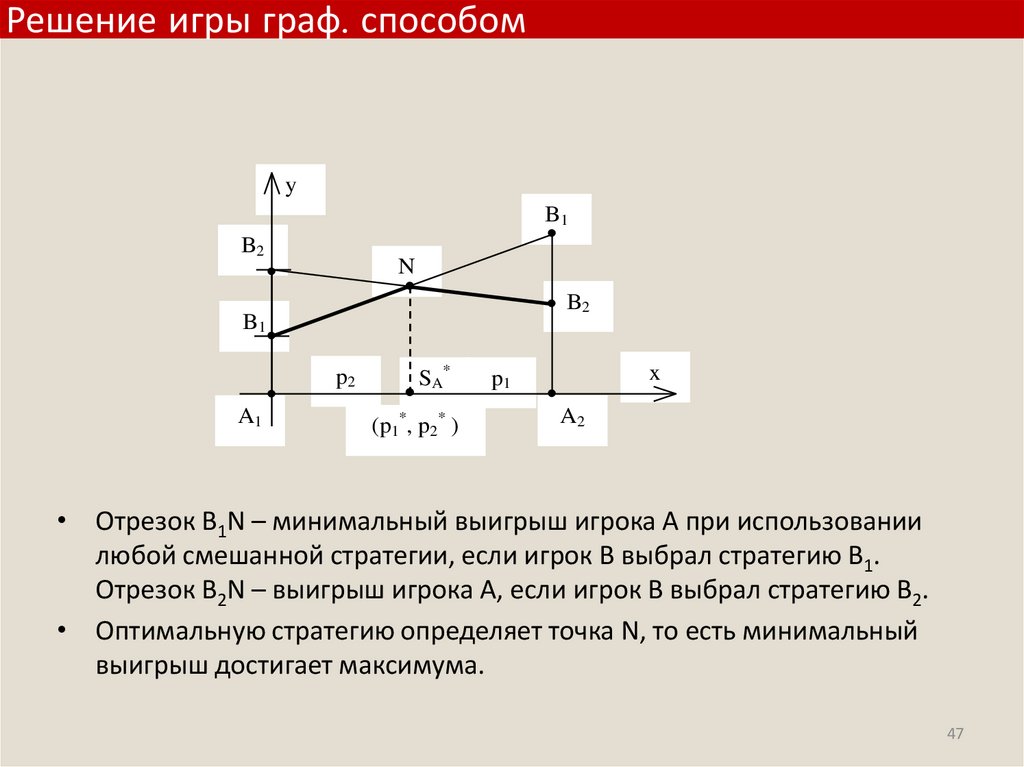
• Отрезок В1N – минимальный выигрыш игрока А при использовании
любой смешанной стратегии, если игрок В выбрал стратегию В1.
Отрезок В2N – выигрыш игрока А, если игрок В выбрал стратегию В2.
• Оптимальную стратегию определяет точка N, то есть минимальный
выигрыш достигает максимума.
47

48.

Алгоритм
1.
2.
3.
4.
5.
Исключить из платежной матрицы заведомо невыгодные стратегии.
Определить верхнюю и нижнюю цены игры и проверить, имеет ли
игра седловую точку.
Если седловая точка есть, то соответствующие ей стратегии игроков
будут оптимальными, а цена совпадает с верхней (нижней) ценой.
Если седловая точка отсутствует, то решение следует искать в
смешанных стратегиях.
Для игр размера m×n рекомендуется симплексный метод, для игр
размера 2×2, 2×n, n×2 возможно геометрическое решение.
48

49.

Пример
https://www.matburo.ru/ex_emm.php?p1=emmti
49

50.

50

51.

51

52.

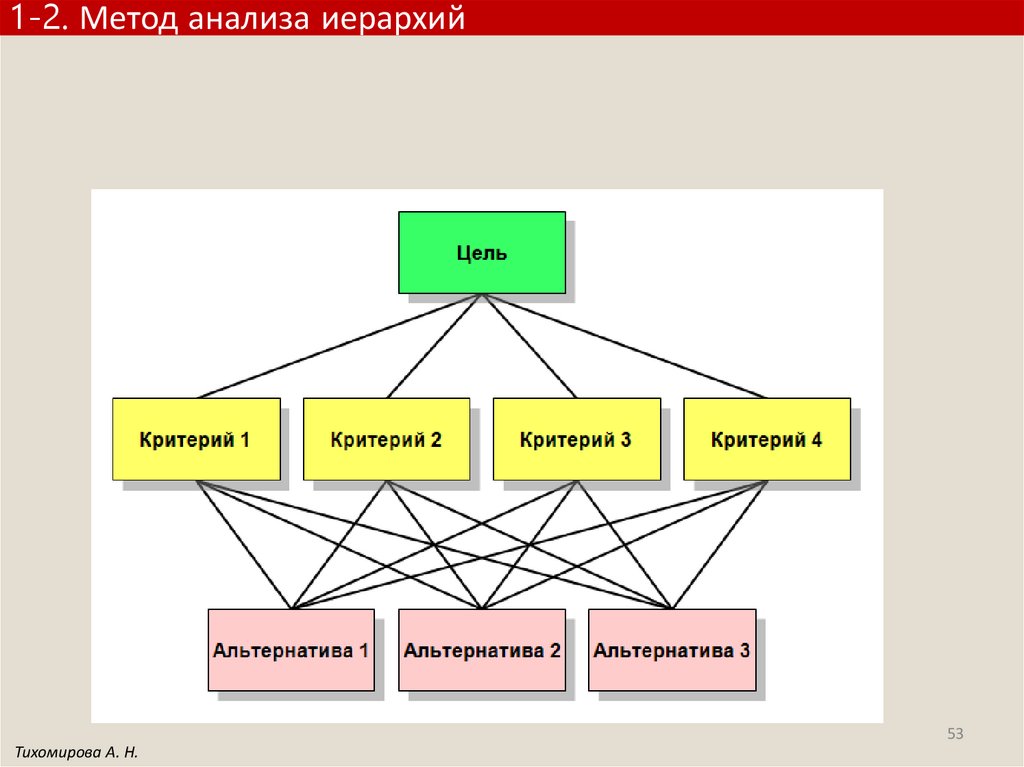
Метод анализа иерархий
Формулировка цели, выбор критериев и альтернатив
Построение дерева иерархии проблемы
Определение относительной важности
Расчет вектора приоритетов
Определение согласованности приоритетов
Корректировка суждений
Иерархический синтез
52
Тихомирова А. Н.

53.

1-2. Метод анализа иерархий
53
Тихомирова А. Н.

54.

3. Правила сравнения
Если элемент Аi доминирует над элементом Аj, то клетка на пересечении строки Аi
и столбца Аj заполняется числовым значением в соответствии со шкалой
относительной важности, а клетка на пересечении строки Аj и столбца Аi –
обратной к этому значению дробью.
Если aij = α , то aji = 1/α , α ≠ 0 .
2. Если элемент Аj доминирует над элементом Аi, то происходит обратное – в клетку
на пересечении строки Аj и столбца Аi записывается числовое значение
относительной важности, а в клетку на пересечении строки Аi и столбца Аj – его
обратная величина (обратная дробь).
3. Если элементы Аi и Аj считаются одинаковыми, то в обе клетки записываются
единицы, т.е. Аi имеет одинаковую с Аj относительную важность, то aij =1 , aji =1; в
частности, aii =1 для всех i.
1.
54
Тихомирова А. Н.

55.

Матрица парных сравнений
Элементы такой матрицы (aij) определяются по указанным выше
правилам, использующим степени предпочтения при сравнении
объектов по заданному критерию, например, в позицию (А,В)
матрицы сравнений ставится число а12, величина которого
выбирается из следующих соображений:
• если А и В одинаково важны (равенство объектов), то ставится
число 1;
• если А имеет предпочтение над В ― число 3;
• если А имеет выраженное предпочтение над В ― число 5;
• если А имеет сильное предпочтение над В ― число 7;
• если А имеет абсолютно предпочтительнее над В ― число 9.
• Числа 2, 4, 6 и 8 используются для облегчения компромиссов
между оценками, слегка отличающимися от основных чисел.
55

56.

4. Расчет вектора приоритетов
Приоритеты — это числа, которые связаны с элементами иерархии.
Они представляют собой относительные веса w1, w2, …, wn элементов в
каждой группе.
Подобно вероятностям, приоритеты — безразмерные величины,
которые могут принимать значения от нуля до единицы.
• Чем больше величина приоритета, тем более значимым является
соответствующий ему элемент.
• Сумма приоритетов элементов, подчиненных одному элементу выше
лежащего уровня иерархии, равна единице. Приоритет цели по
определению равен 1.
56
Тихомирова А. Н.

57.

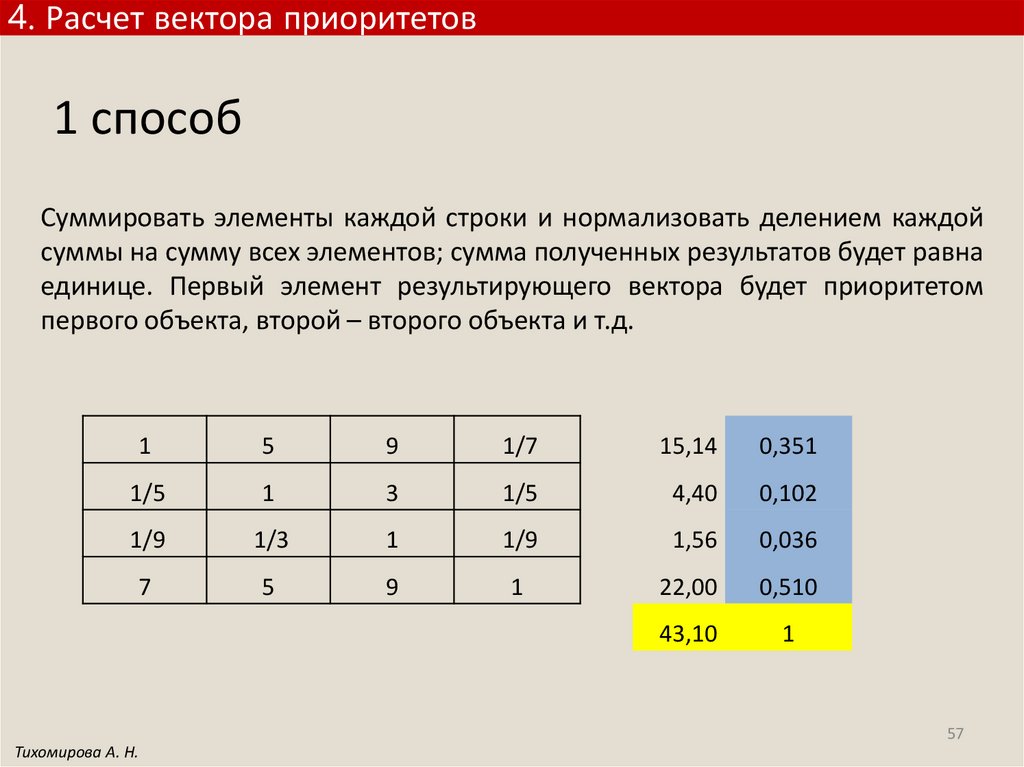
4. Расчет вектора приоритетов
1 способ
Суммировать элементы каждой строки и нормализовать делением каждой
суммы на сумму всех элементов; сумма полученных результатов будет равна
единице. Первый элемент результирующего вектора будет приоритетом
первого объекта, второй – второго объекта и т.д.
1
5
9
1/7
15,14
0,351
1/5
1
3
1/5
4,40
0,102
1/9
1/3
1
1/9
1,56
0,036
7
5
9
1
22,00
0,510
43,10
1
57
Тихомирова А. Н.

58.

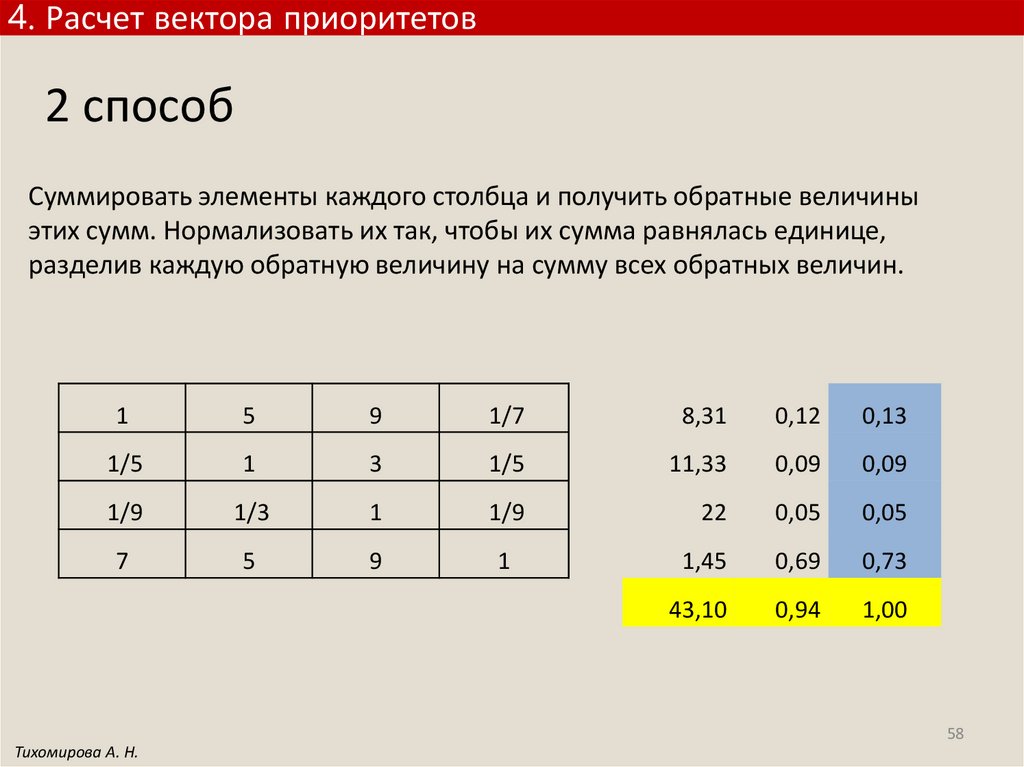
4. Расчет вектора приоритетов
2 способ
Суммировать элементы каждого столбца и получить обратные величины
этих сумм. Нормализовать их так, чтобы их сумма равнялась единице,
разделив каждую обратную величину на сумму всех обратных величин.
1
5
9
1/7
8,31
0,12
0,13
1/5
1
3
1/5
11,33
0,09
0,09
1/9
1/3
1
1/9
22
0,05
0,05
7
5
9
1
1,45
0,69
0,73
43,10
0,94
1,00
58
Тихомирова А. Н.

59.

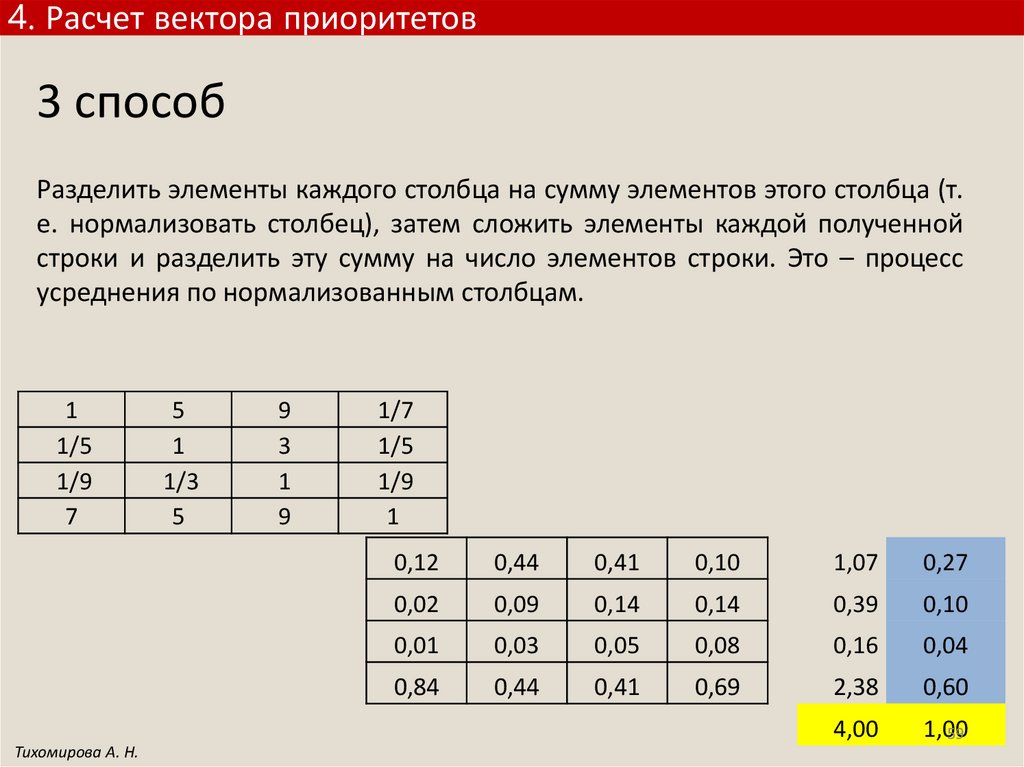
4. Расчет вектора приоритетов
3 способ
Разделить элементы каждого столбца на сумму элементов этого столбца (т.
е. нормализовать столбец), затем сложить элементы каждой полученной
строки и разделить эту сумму на число элементов строки. Это – процесс
усреднения по нормализованным столбцам.
1
1/5
1/9
7
Тихомирова А. Н.
5
1
1/3
5
9
3
1
9
1/7
1/5
1/9
1
0,12
0,44
0,41
0,10
1,07
0,27
0,02
0,09
0,14
0,14
0,39
0,10
0,01
0,03
0,05
0,08
0,16
0,04
0,84
0,44
0,41
0,69
2,38
0,60
4,00
1,00
59

60.

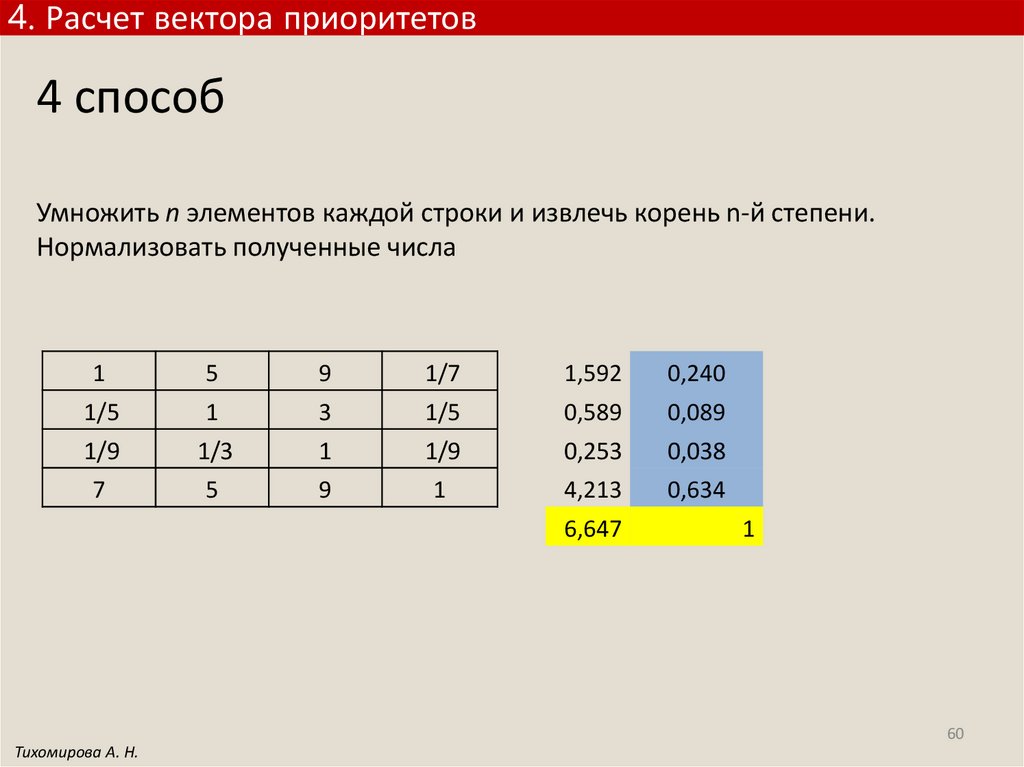
4. Расчет вектора приоритетов
4 способ
Умножить n элементов каждой строки и извлечь корень n-й степени.
Нормализовать полученные числа
1
5
9
1/7
1,592
0,240
1/5
1
3
1/5
0,589
0,089
1/9
1/3
1
1/9
0,253
0,038
7
5
9
1
4,213
0,634
6,647
1
60
Тихомирова А. Н.

61.

5. Определение согласованности приоритетов
Если анализируется матрица с результатами, полученными с помощью точных
физических измерений (например, высоты, массы и т.д.), то значения элементов
матрицы транзитивны: если некоторый объект А1 предпочтительнее объекта А2
в k раз, а объект А2 предпочтительнее объекта А3 в m раз, то объект А1
предпочтительнее объекта А3 в k*m раз.
В практических задачах количественная (кардинальная) и транзитивная
(порядковая) согласованность нарушается, поскольку человеческие ощущения
нельзя выразить точной формулой. В реальной жизни достигнуть такой точности
экспертизы сложно, поэтому необходимо ввести параметр, определяющий
насколько отличаются индексы согласованности для произвольной и
заполненной экспертом матрицы.
Для улучшения однородности в числовых суждениях, какая бы величина aij ни
была взята для сравнения i-го элемента с j-м, aij приписывается значение
обратной величины, т. е. аij = 1/aij. Отсюда следует, что если один элемент в а раз
предпочтительнее другого, то последний только в 1/а раз предпочтительнее
первого.
61
Тихомирова А. Н.

62.

5. Определение согласованности приоритетов
Пусть A — это квадратная матрица.
Вектор v называется собственным вектором матрицы A, если
Av = λv, где число λ называется собственным значением матрицы A.
Таким образом преобразование, которое выполняет матрица A над
вектором v, сводится к простому растяжению или сжатию с
коэффициентом λ.
Для оценки однородности матрицы (согласованности суждений
эксперта)
необходимо
использовать
отклонение
величины
максимального* собственного значения λmax от порядка матрицы п.
*В работе далее вместо максимального собственного значения будет
использоваться среднее значение различных λ.
62
Тихомирова А. Н.

63.

5. Определение согласованности приоритетов
Для исходной матрицы посчитаем
1.
Приоритеты
2.
Сумма по всем хi = 6,647.
1
1/5
1/9
7
5
1
1/3
5
9
3
1
9
1/7
1/5
1/9
1
3. Вес каждого критерия
63
Тихомирова А. Н.

64.

5. Определение согласованности приоритетов
4.
Умножаем матрицу относительной важности на вектор
приоритетов. Например, для первой строки (для всех остальных,
аналогично).
5.
Затем делим каждую компоненту нового вектора на
соответствующую компоненту вектора приоритетов (для всех
остальных, аналогично).
6.
Полученные значения необходимо просуммировать и разделить на
число компонент вектора, получим λmax – собственное значение.
64
Тихомирова А. Н.

65.

5. Определение согласованности приоритетов
7.
Расчет индекса согласованности:
8.
Расчет отношения согласованности:
СС — среднее значение (математическое ожидание) индекса согласованности
случайным образом составленной матрицы парных сравнений, которое
основано на экспериментальных данных.
Размер
матрицы
СС
1
2
3
4
5
6
7
8
9
10
0
0
0,58
0,90
1,12
1,24
1,32
1,41
1,45
1,49
65
Тихомирова А. Н.

66.

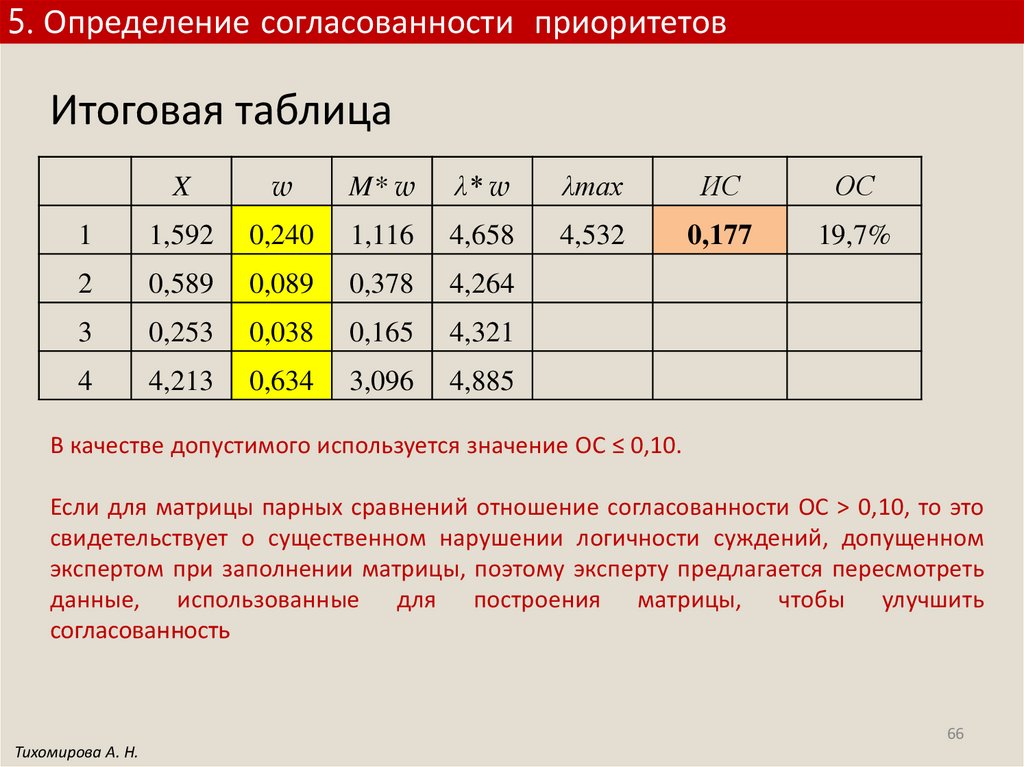
5. Определение согласованности приоритетов
Итоговая таблица
X
w
M* w
λ* w
λmax
ИС
ОС
1
1,592
0,240
1,116
4,658
4,532
0,177
19,7%
2
0,589
0,089
0,378
4,264
3
0,253
0,038
0,165
4,321
4
4,213
0,634
3,096
4,885
В качестве допустимого используется значение OС ≤ 0,10.
Если для матрицы парных сравнений отношение согласованности OС > 0,10, то это
свидетельствует о существенном нарушении логичности суждений, допущенном
экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть
данные, использованные для построения матрицы, чтобы улучшить
согласованность
66
Тихомирова А. Н.

67.

6. Корректировка суждений
1.
Найти строку i:
n
max i aij
j 1
2.
wi
wj
0
0,169
0,047
4,354
2,294
0
0,102
3,201
2,713
0,676
0
7,633
0,235
0,060
0,051
0
5,242
0,906
0,201
15,189
Заменить все aij на wi/wj в этой строке, а в соответствующем столбце
поставить их обратные величины.
1,00
0,20
0,11
2,65
5,00
1,00
0,33
7,16
9,00
3,00
1,00
16,63
0,38
0,14
0,06
1,00
67
Тихомирова А. Н.

68.

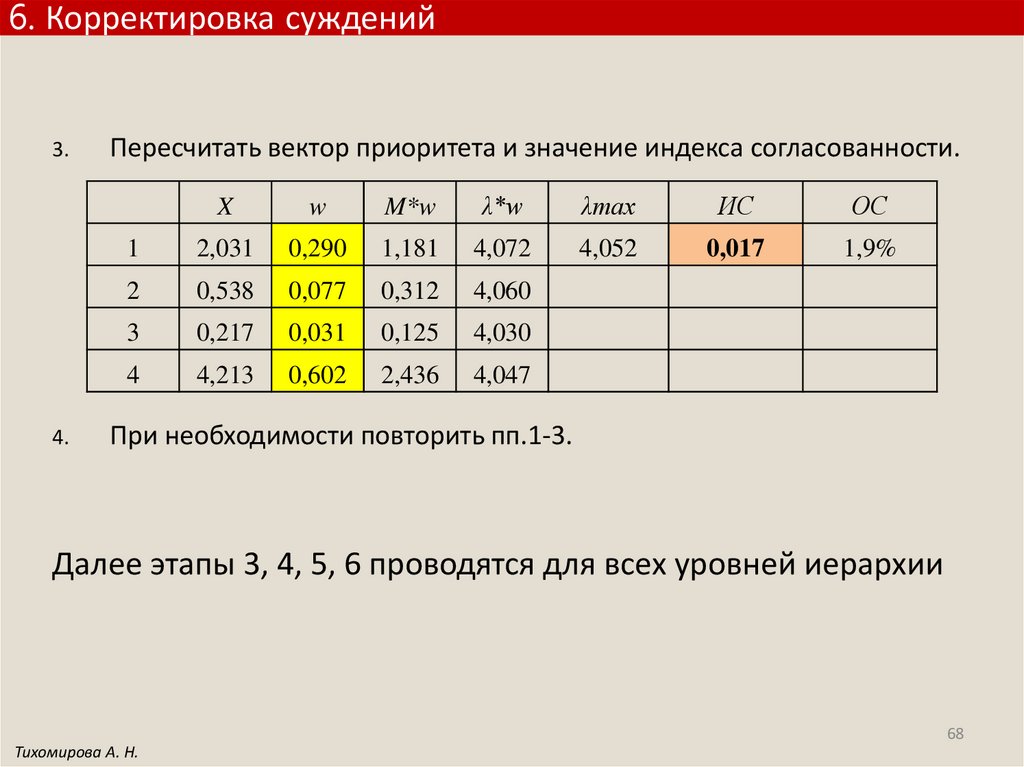
6. Корректировка суждений
3.
4.
Пересчитать вектор приоритета и значение индекса согласованности.
X
w
M*w
λ*w
λmax
ИС
ОС
1
2,031
0,290
1,181
4,072
4,052
0,017
1,9%
2
0,538
0,077
0,312
4,060
3
0,217
0,031
0,125
4,030
4
4,213
0,602
2,436
4,047
При необходимости повторить пп.1-3.
Далее этапы 3, 4, 5, 6 проводятся для всех уровней иерархии
68
Тихомирова А. Н.

69.

7. Иерархический синтез
1.
2.
3.
Составить матрицу, в которой столбцы – это векторы приоритетов
каждой из альтернатив по конкретному критерию. Если в иерархии
было N альтернатив и M критериев, то в матрице получится N строк и M
столбцов
Для того, чтобы получить оценку альтернатив, необходимо умножить
полученную матрицу на вектор приоритетов критериев. Т.о. будет
умножена матрица размерности N*M на вектор размерности M. В
результате будет получен вектор размерности N, значения элементов
которого и соответствует предпочтительности альтернатив с точки
зрения достижимости поставленной цели.
Из полученного вектора следует выбирать альтернативу с наибольшим
значением в полученном векторе.
69
Тихомирова А. Н.

70.

Пример - Задача о выборе школы
Необходимо проанализировать школы А, В, С на предмет их
желательности с точки зрения конкретного ребенка. Для
сравнения были выбраны шесть независимых характеристик
(критерии):
1. Учеба (У)
2. Друзья (Д)
3. Школьная жизнь (Ж)
4. Профессиональное обучение (П)
5. Подготовка к колледжу (К)
6. Обучение музыке (М)
70
Тихомирова А. Н.

71.

1. Формулировка цели, выбор критериев и альтернатив
Цель: анализ школ.
Критерии:
1. Учеба (У)
2. Друзья (Д)
3. Школьная жизнь (Ж)
4. Профессиональное обучение (П)
5. Подготовка к колледжу (К)
6. Обучение музыке (М)
Альтернативы: школы А, В, С.
71
Тихомирова А. Н.

72.

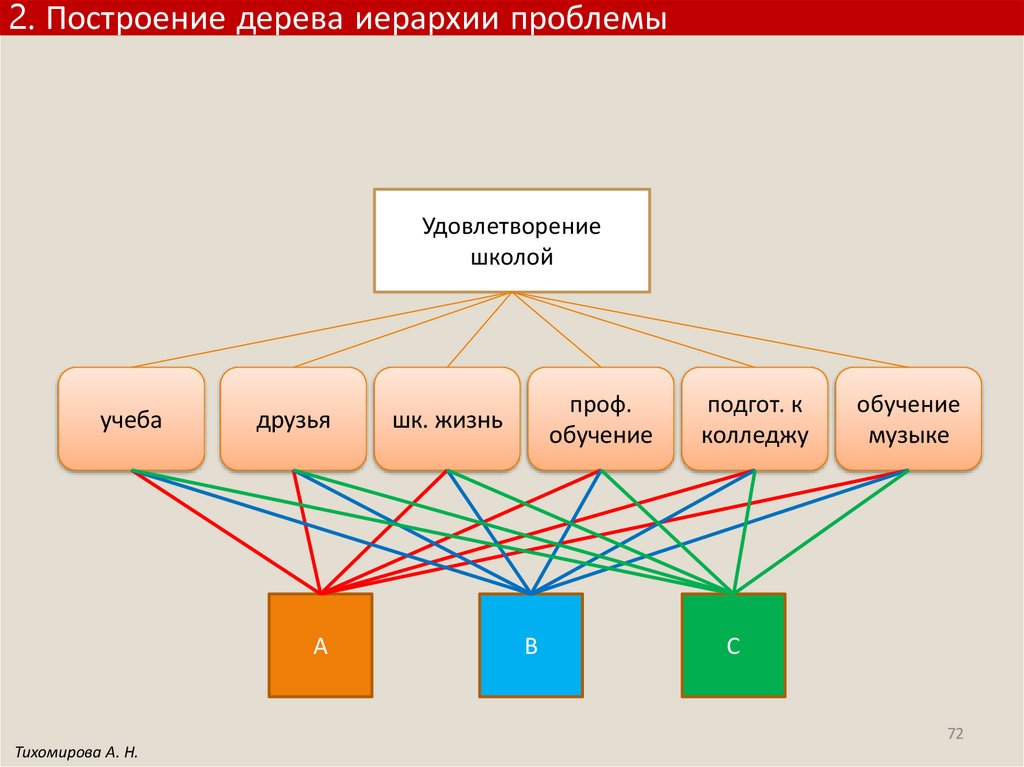
2. Построение дерева иерархии проблемы
Удовлетворение
школой
учеба
друзья
А
проф.
обучение
шк. жизнь
В
подгот. к
колледжу
обучение
музыке
С
72
Тихомирова А. Н.

73.

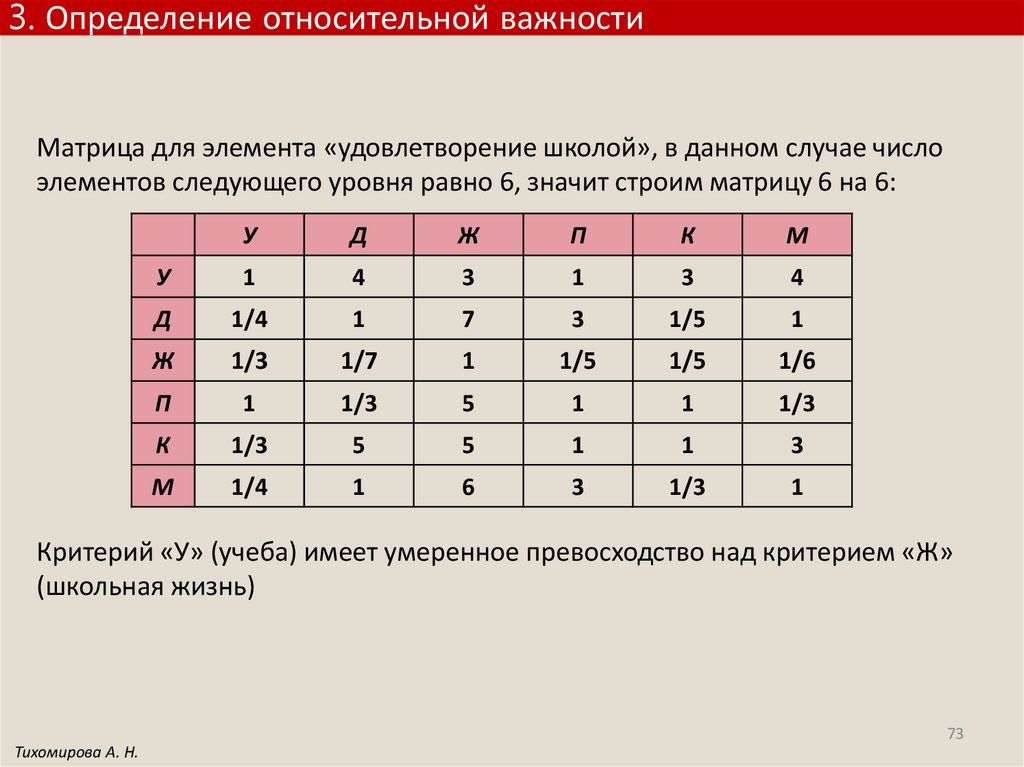
3. Определение относительной важности
Матрица для элемента «удовлетворение школой», в данном случае число
элементов следующего уровня равно 6, значит строим матрицу 6 на 6:
У
Д
Ж
П
К
М
У
1
4
3
1
3
4
Д
1/4
1
7
3
1/5
1
Ж
1/3
1/7
1
1/5
1/5
1/6
П
1
1/3
5
1
1
1/3
К
1/3
5
5
1
1
3
М
1/4
1
6
3
1/3
1
Критерий «У» (учеба) имеет умеренное превосходство над критерием «Ж»
(школьная жизнь)
73
Тихомирова А. Н.

74.

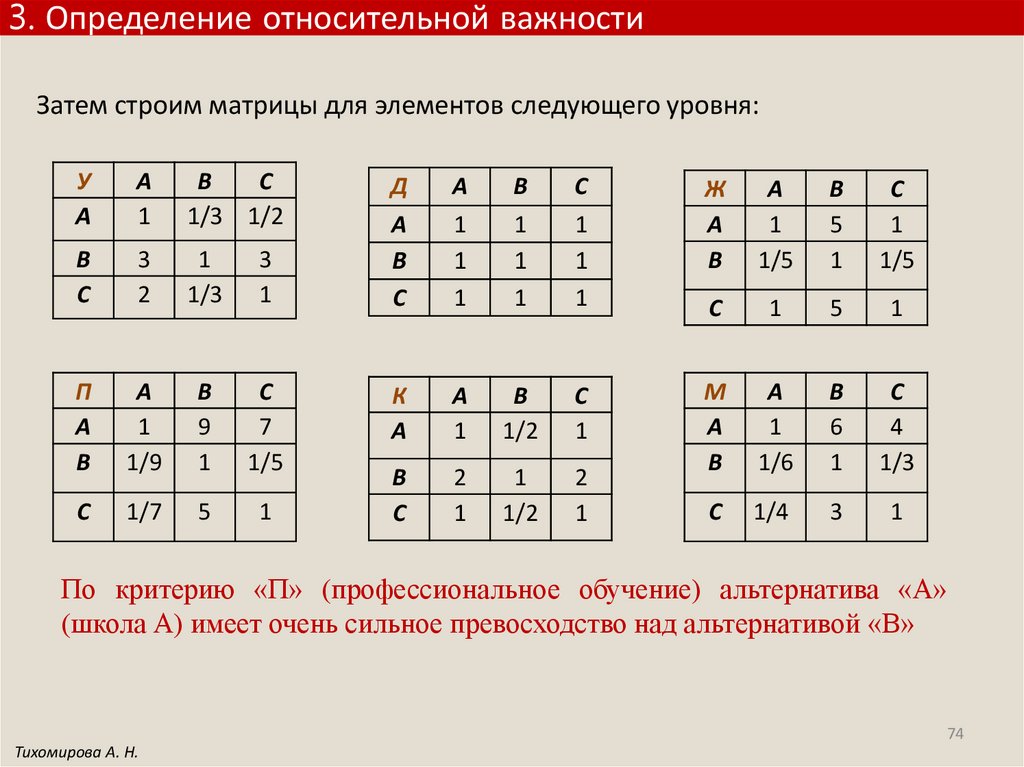
3. Определение относительной важности
Затем строим матрицы для элементов следующего уровня:
У
А
А
1
В
С
1/3 1/2
В
С
3
2
1
1/3
3
1
П
А
В
А
1
1/9
В
9
1
С
7
1/5
С
1/7
5
1
Д
А
В
С
А
1
1
1
В
1
1
1
С
1
1
1
Ж
А
В
А
1
1/5
В
5
1
С
1
1/5
С
1
5
1
К
А
А
1
В
1/2
С
1
В
С
2
1
1
1/2
2
1
М
А
В
А
1
1/6
В
6
1
С
4
1/3
С
1/4
3
1
По критерию «П» (профессиональное обучение) альтернатива «А»
(школа А) имеет очень сильное превосходство над альтернативой «В»
74
Тихомирова А. Н.

75.

4. Расчет вектора приоритетов
Рассчитаем векторы приоритетов для задачи (3-ий способ):
Для матрицы «удовлетворение школой»:
Посчитаем сумму по каждому столбцу:
Сстолб = (3,16; 11,47; 27; 9,2; 5,73; 9,5)
Каждый элемент исходной матрицы разделим на сумму того столбца, в
котором он стоит, получаем следующую матрицу:
75
Тихомирова А. Н.

76.

4. Расчет вектора приоритетов
Суммируем элементы в каждой строке и делим на число элементов в этой
строке, полученный вектор и будет вектором приоритетов, сумма
компонентов которого должна равняться единице:
76
Тихомирова А. Н.

77.

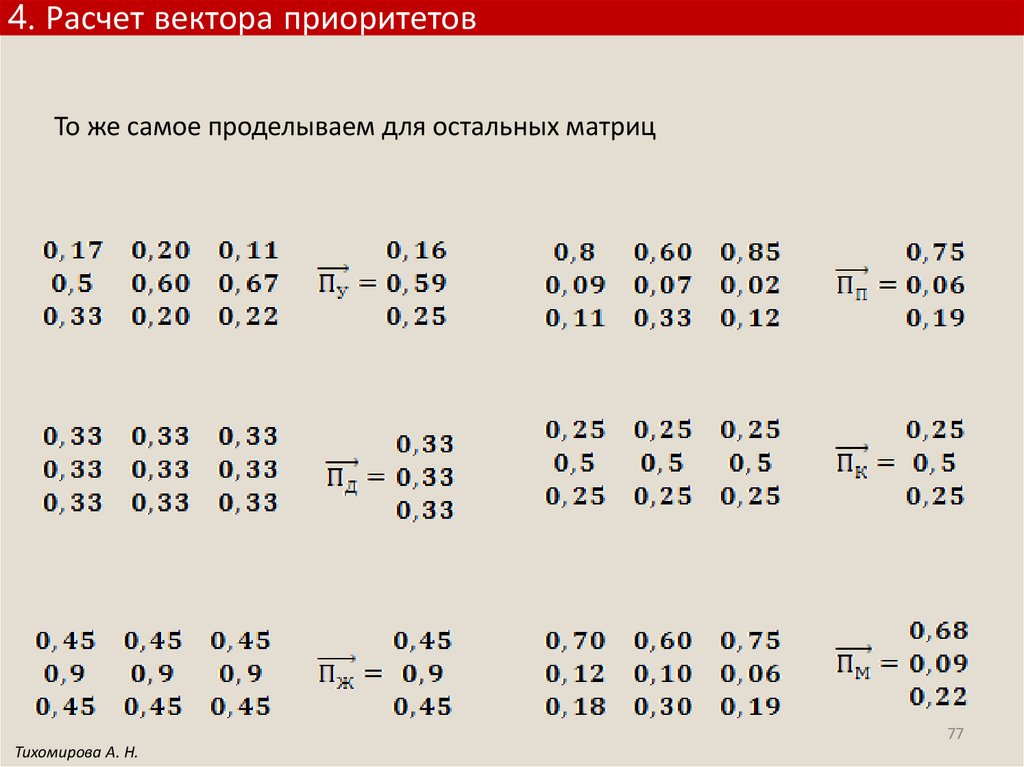
4. Расчет вектора приоритетов
То же самое проделываем для остальных матриц
77
Тихомирова А. Н.

78.

5. Определение согласованности приоритетов
Определим согласованность приоритетов для нашего примера:
Умножаем матрицу относительной важности на вектор приоритетов, затем
делим каждую компоненту нового вектора на соответствующую компоненту
вектора приоритетов. Полученные значения необходимо просуммировать и
разделить на число компонент вектора, получим λmax –собственное значение.
78
Тихомирова А. Н.

79.

5. Определение согласованности приоритетов
У
Д
Ж
79
Тихомирова А. Н.

80.

5. Определение согласованности приоритетов
П
К
М
80
Тихомирова А. Н.

81.

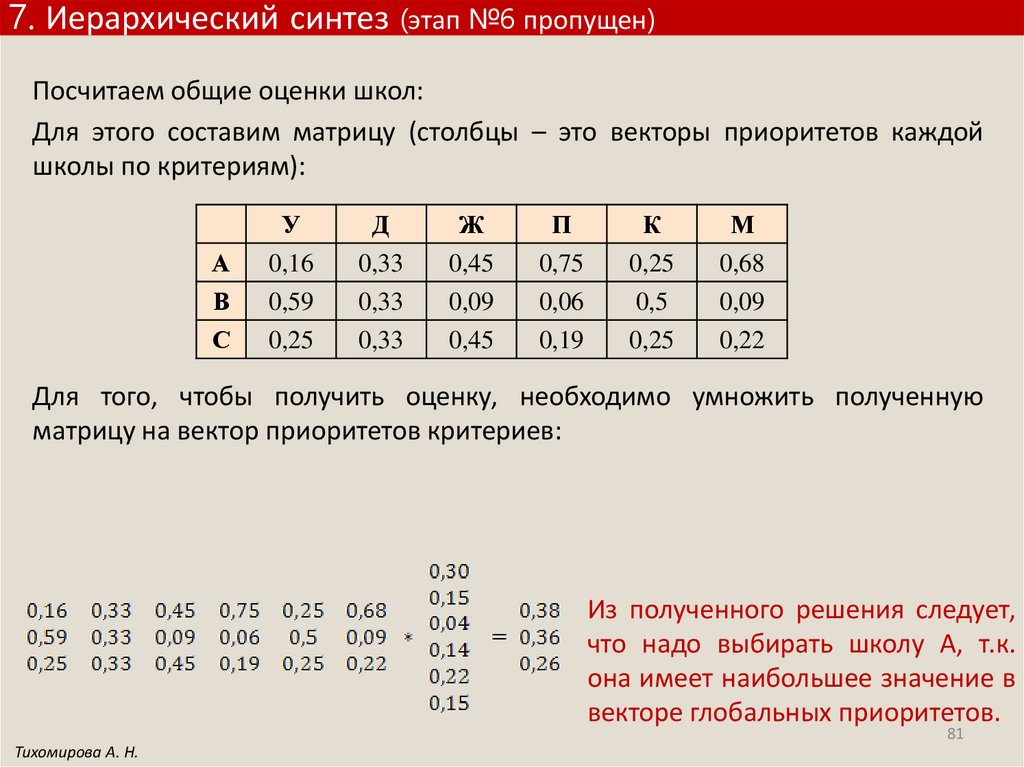
7. Иерархический синтез (этап №6 пропущен)
Посчитаем общие оценки школ:
Для этого составим матрицу (столбцы – это векторы приоритетов каждой
школы по критериям):
А
В
С
У
0,16
0,59
0,25
Д
0,33
0,33
0,33
Ж
0,45
0,09
0,45
П
0,75
0,06
0,19
К
0,25
0,5
0,25
М
0,68
0,09
0,22
Для того, чтобы получить оценку, необходимо умножить полученную
матрицу на вектор приоритетов критериев:
Из полученного решения следует,
что надо выбирать школу А, т.к.
она имеет наибольшее значение в
векторе глобальных приоритетов.
81
Тихомирова А. Н.

82.

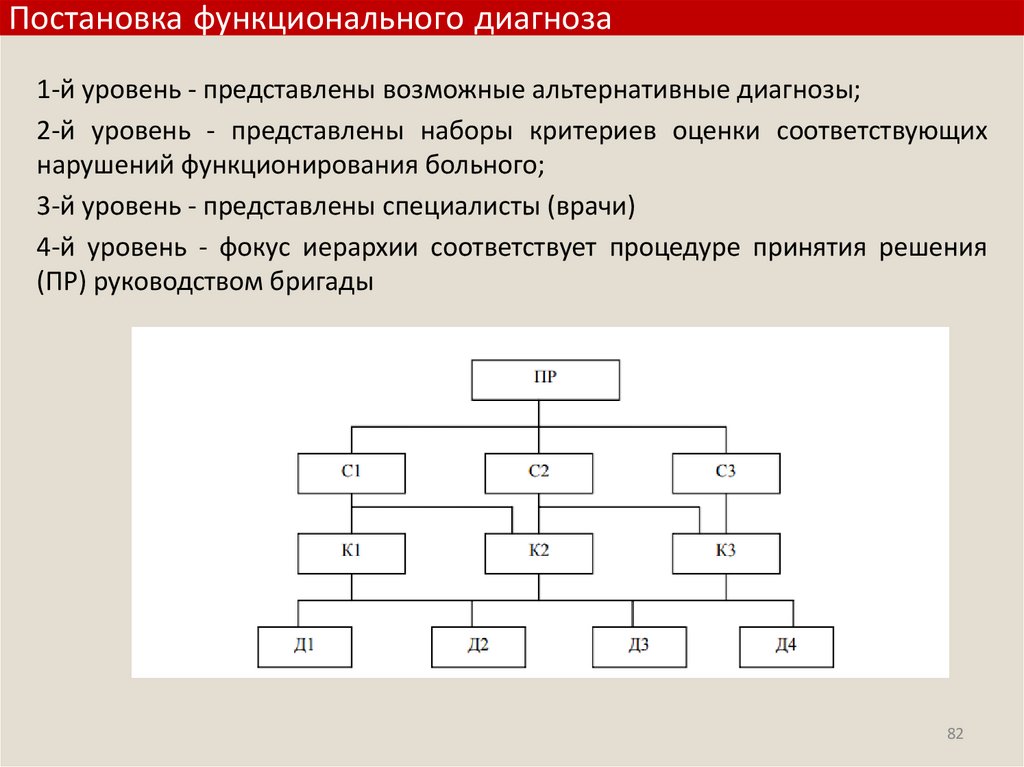
Постановка функционального диагноза
1-й уровень - представлены возможные альтернативные диагнозы;
2-й уровень - представлены наборы критериев оценки соответствующих
нарушений функционирования больного;
3-й уровень - представлены специалисты (врачи)
4-й уровень - фокус иерархии соответствует процедуре принятия решения
(ПР) руководством бригады
82