Похожие презентации:
Многочастотные динамические системы
1.
ТЕОРИЯ КОЛЕБАНИЙТема 7. Многочастотные динамические системы.
Томск 2022
2.
Многочастотные колебательные системыПримеры:
1. Кристаллическая решетка. Отдельные узлы можно рассматривать как
осцилляторы.
2. Связанные автогенераторы. Ярким примером будет магнетрон,
который широко используется в СВЧ электронике.
• В конструкцию магнетрона входит четное число связанных
четвертьволновых резонаторов и пара постоянных магнитов.
• В магнитном поле возникает круговое движение зарядов, что
создает электрический ток, который возбуждает резонаторы.
• В обычной электронике используется система нескольких
колебательных контуров, которые соединены круговым
проводом.
3. Стая журавлей. Журавли летят клином и каждый из журавлей
пытается лететь синхронно с вожаком. Но у крайних журавлей
возникают задержки.
4. Балочный мост.
3.
В рассмотренных примерах систем всегда известно число степенейсвободы. Возникает вопрос: всегда ли известно число степеней свободы в
многочастотных системах?
Ответ: не всегда число степеней свободы может быть определенно у
системы.
Примеры: системы с запаздывающей обратной связью, распределенные
структуры.
Поэтому можно ввести классификацию многочастотных колебательных
систем по числу степеней свободы:
1. Системы с определенным числом степеней свободы.
2. Системы с неопределенным числом степеней свободы.
4.
Рассмотрим систему связанных маятников:Нить нерастяжима.
Маятники связаны пружинами.
Маятники не колеблются индивидуально, т.е. наличие пружины будет влиять
на все маятники.
i
i
св ,i
- частота свободных колебаний индивидуального маятника
- парциальная частота (когда все, кроме i-того, маятники закреплены,
но связь пружиной присутствует).
- частоты свободных колебаний системы.
5.
Математическая модель системы маятниковДля каждого маятника можно записать уравнение движения:
n
2
x1 2 1 x1 1 x1 ( i xi i xi i xi )
i 2
n
2
x2 2 2 x2 2 x2 ( i xi i xi i xi )
i 1
i 2
...
...
Количество уравнений будет совпадать с числом степеней свободы системы.
Это уравнения линейной системы.
6.
В этом курсе мы рассматриваем нелинейные случаи. Тогдаi , i , i , ,
будут нелинейными функциями
i
- коэффициент силовой связи
i
- коэффициент диссипационной связи
i
- коэффициент инерционной связи
f (x, x)
7.
Многочастотные системы с неопределенным числом степеней свободы.Рассмотрим усилитель К0
с задержкой
, который имеет обратную связь
AK 0 cos t AK 0 cos t AK 0 cos t
При изменении частоты сигнал на вход будет приходить либо синфазно,
либо противофазно.
Таким образом, в системе будет имеет место чередование положительной
и отрицательной обратной связи.
При βK0>1 в системе возникает возбуждение колебаний на всех частотах,
на которых выполнено условие синфазности.
При наличии фильтра можно выделить частоты. Это позволит
ограничить степени свободы, тогда система будет иметь определенное
число степеней свободы.
8.
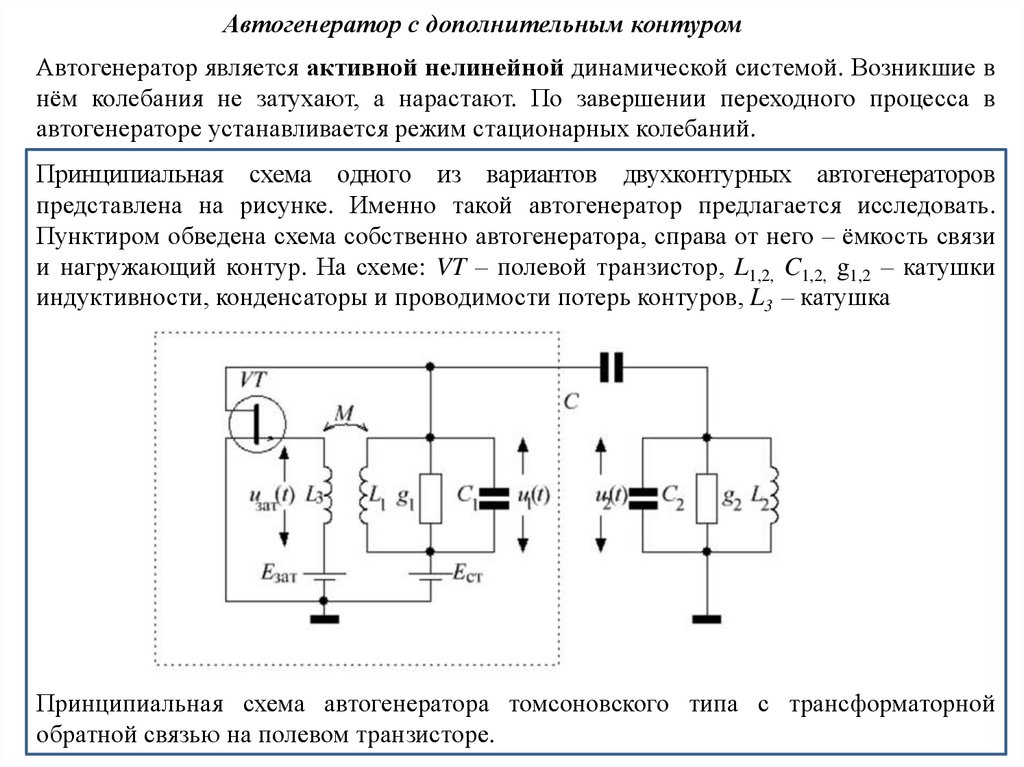
Двухконтурный автогенераторДвухконтурный автогенератор состоит из двух связанных колебательных контуров,
один из которых входит в структуру автогенератора, то есть, регенерирован и является
активным. А второй – пассивен и нагружает автогенератор. Простейший вариант
автогенератора показан на рисунке.
Связанные контуры. Здесь L1,2, C1,2 и g1,2 – индуктивности, ёмкости и
проводимости потерь первого и второго контуров, Y – элемент связи (C, L или g), N –
негатрон – активный двухполюсник с падающим участком вольтамперной
характеристики (например, туннельный диод), компенсирующий потери первого
контура.
Связь контуров может осуществляться с помощью энергоёмких или диссипативных
элементов. К числу первых относятся конденсатор (силовая связь), а также катушка
самоиндукции или трансформатор (инерциальная связь). К числу диссипативных
элементов относятся резисторы любого типа. Часто связь через энергоёмкие элементы
называют реактивной, а через диссипативные элементы – резистивной.
9.
Свойства системы двух реактивно связанных пассивных линейных колебательныхконтуров
Прежде чем обсуждать свойства двухконтурного автогенератора полезно вспомнить
основные особенности системы двух контуров, связанных энергоёмким элементом, в
частности – конденсатором (рис.).В рассматриваемой схеме в процессе колебаний
происходит обмен энергиями между контурами. Кроме того, так как система имеет
две степени свободы, то при определённых условиях колебания могут происходить на
одной или двух собственных частотах. Именно это приводит к тому, что в системе
возможно возбуждение различных видов движений. Частоты свободных
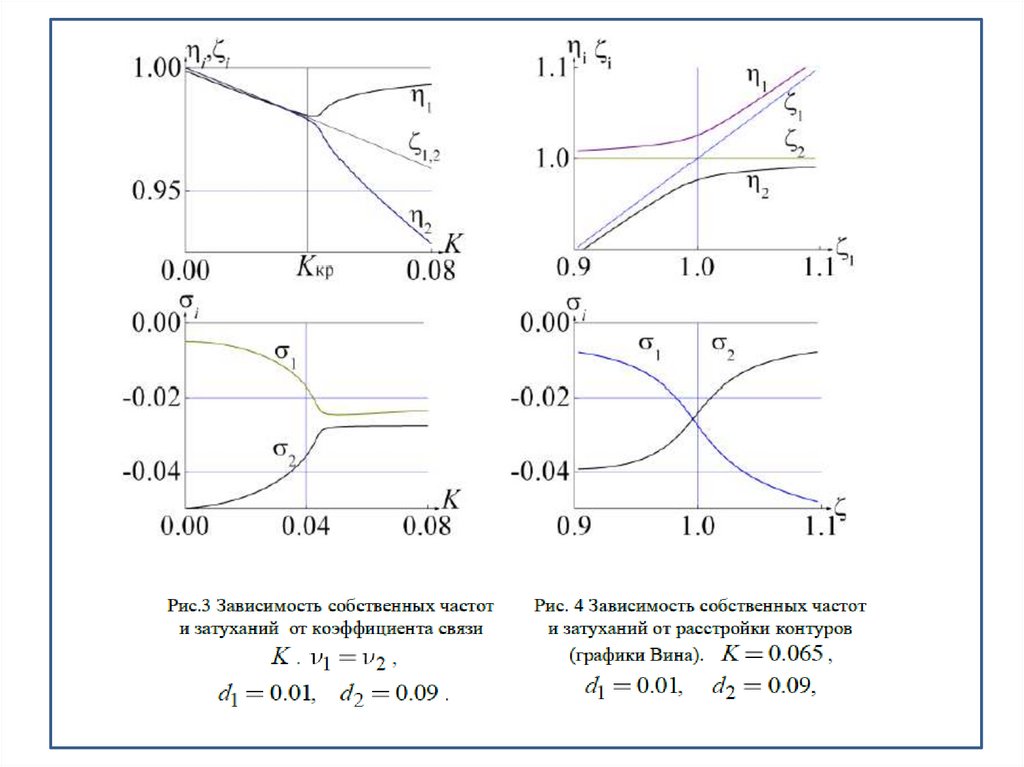
(собственных) колебаний зависят от величины связи контуров и от расстройки контуров. Эти зависимости находятся из решения уравнений движения системы.
Система двух контуров, связанных конденсатором.
10.
Напомним, что резонансные частоты изолированных контуров определяютсяформулой Томсона
а резонансные частоты и собственные затухания парциальных систем, то есть
парциальные частоты и затухания, записываются в виде:
(парциальной является система, когда один контур закорочен, а элемент связи
подключён параллельно другому контуру).
Коэффициент связи контуров равен:
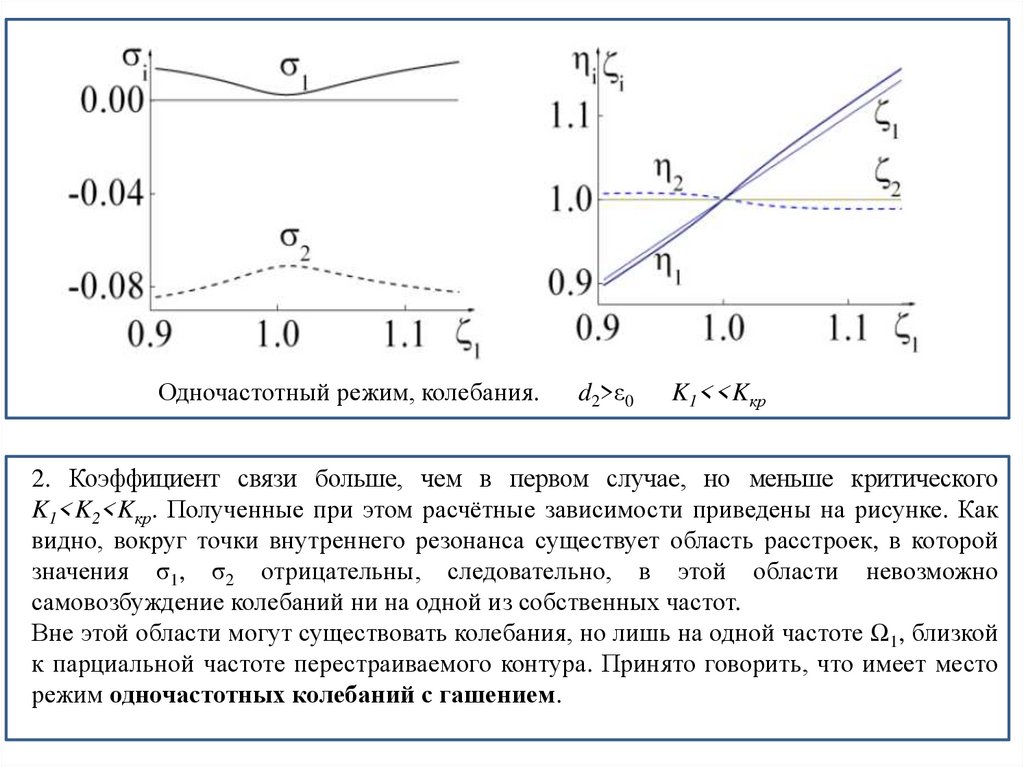
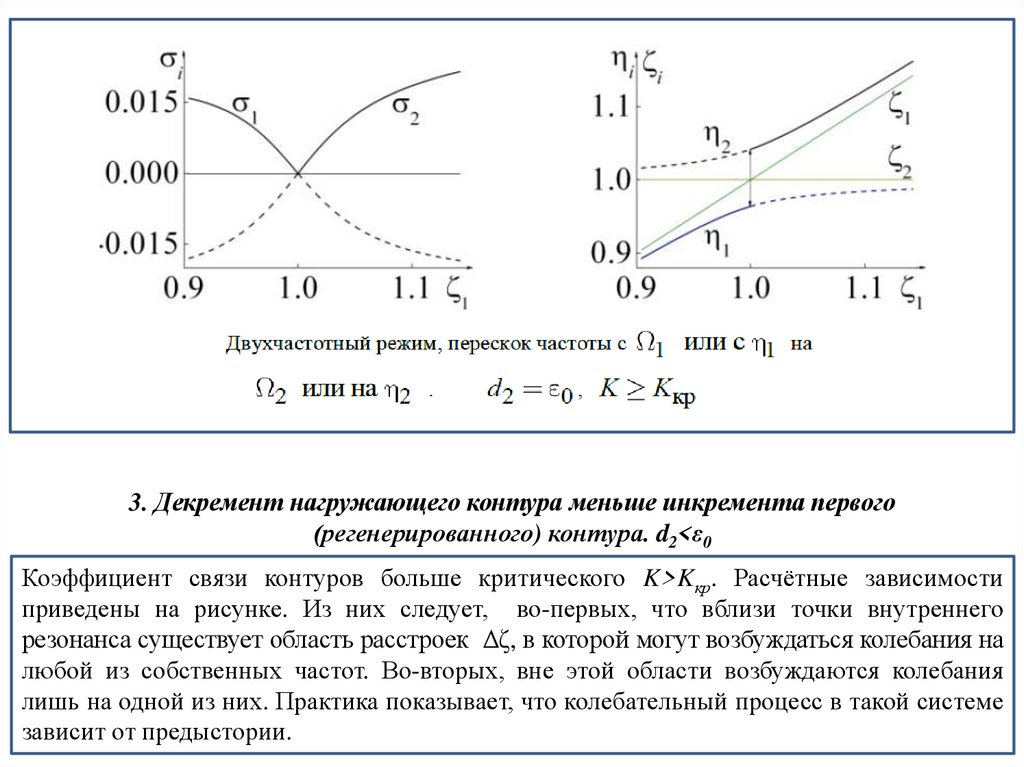
Если парциальные частоты контуров одинаковы, то принято говорить, что в системе
имеет место внутренний резонанс.
11.
Решение системы ищется в видегде A, B– собственные векторы, зависящие от начальных условий, а λ – собственные
значения, являющиеся корнями характеристического полинома
Как видим, это уравнение четвёртой степени, решение которого для колебательных
систем имеет вид пары комплексно сопряжённых чисел:
где Ω1,2 – частоты, а σ1,2– декременты затуханий свободных колебаний. Отсюда следует,
что рассматриваемая система действительно является двухчастотной, а напряжения
записываются как:
12.
Здесь k1, k2 – коэффициенты распределения амплитуд, φ1,φ2 – начальные фазы,определяемые, как A и B, начальными условиями.
Далее удобно расчёты вести относительно частот, нормированных к парциальной
частоте неперестраиваемого контура υ2, то есть





















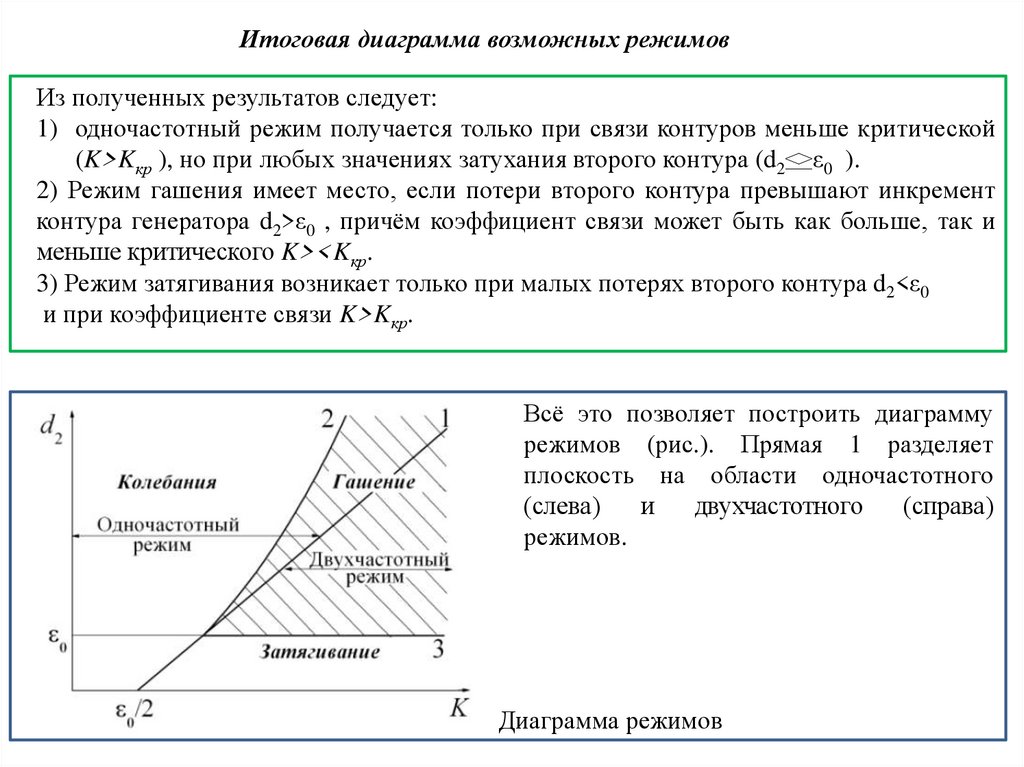




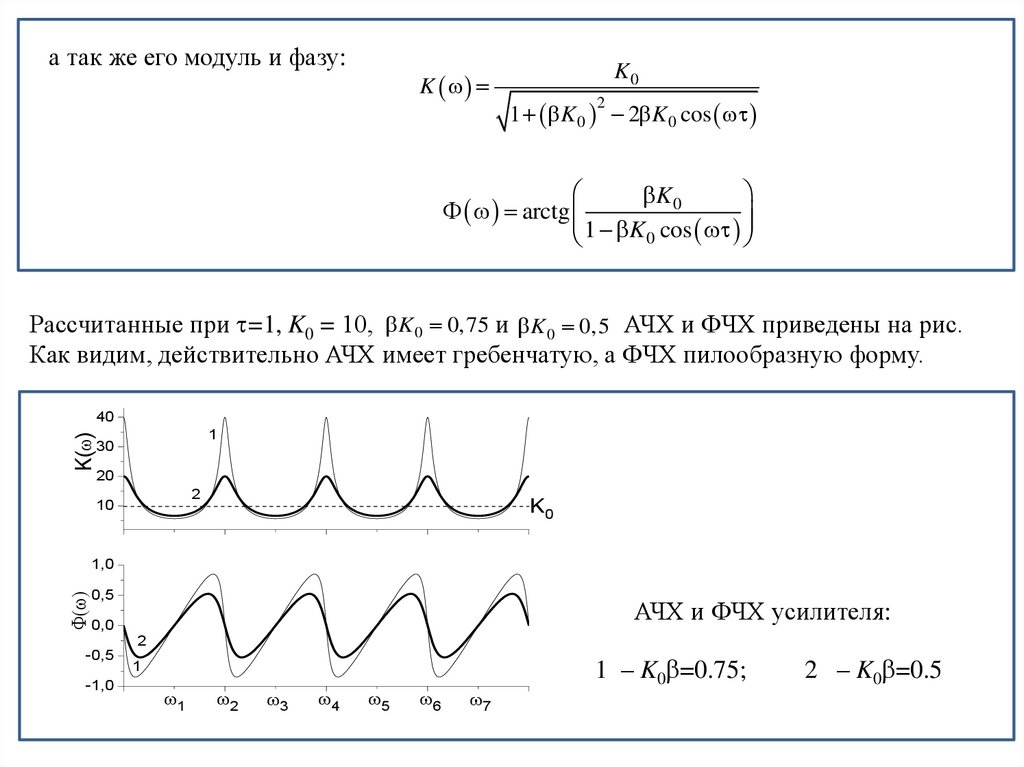


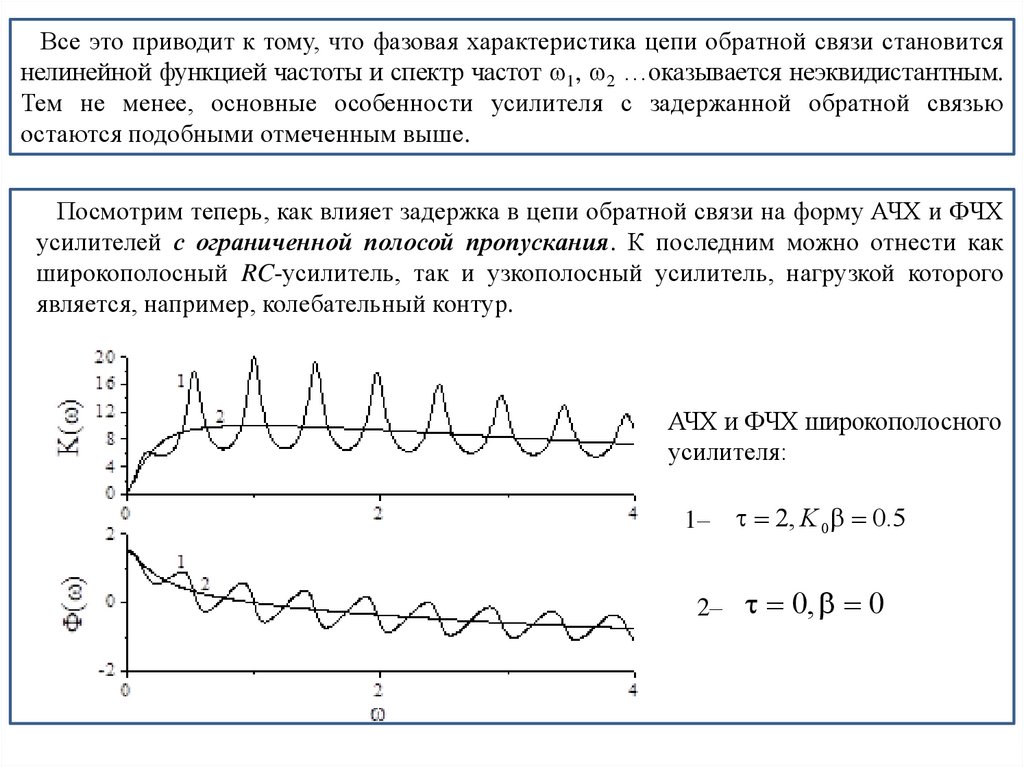
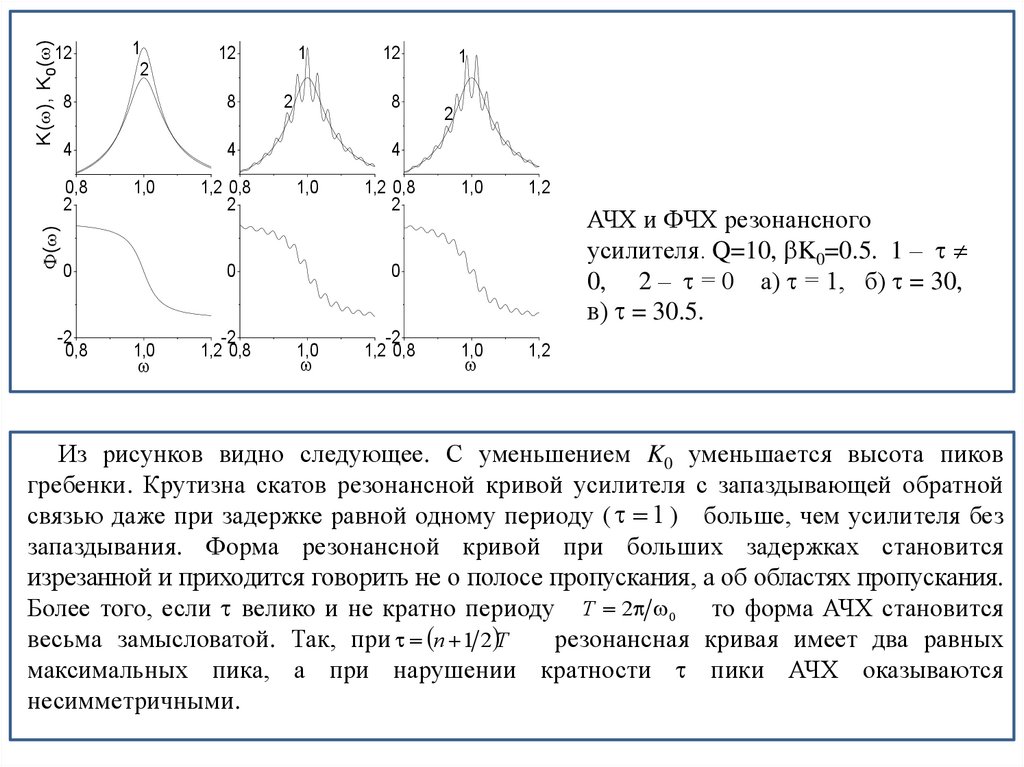








 Физика
Физика








