Похожие презентации:
Решение неравенств
1.
Краснооктябрьская СОШСеменов. К.А. и
2.
Виды неравенств- Линейные
kx> b , k≠ 0
b
x > если k > 0
k
b
x < если k < 0
k
- Квадратные
2
ax + bx+ c> 0 ( a> 0, a< 0)
_
+
x1
+
x2
x
3.
Виды неравенствA( x)
>0
B( x)
- Рациональные
_
_
+
x1
x2
+
x3
x
4.
Виды неравенств- Содержащие чётную степень
2n
x >b
x< − √b , x> √b , если b> 0
x< 0 , x> 0 , если b= 0
x∈ R , если b< 0
2n
2n
- Содержащие нечётную степень x
x>
√b
2 n+ 1
2 n+ 1
>b
5.
Виды неравенств- Иррациональные (корень чётной степени)
√x> b
2n
2n
x> b если b> 0
x> 0 если b= 0
x≥0 если b< 0
- Иррациональные (корень нечётной степени)
√x> b
2 n+ 1
2n+ 1
x> b
6.
Виды неравенств- Показательные
x
a > b если a> 1
x> log a b если b> 0
x∈ R если b< 0
x
a > b если 0< a< 1
x< log a b если b> 0
x∈ R если b< 0
7.
Виды неравенств- Логарифмические
loga x> b если a> 1
loga x> b если 0< a< 1
x> a
b
b
0< x< a
- Тригонометрические
Решаем неравенства, используя
тригонометрическую окружность, либо с
помощью графика соответствующей
функции
8.
Равносильность неравенств1.Перенос члена неравенства (с противоположным
знаком) из одной части неравенства в другую;
2. Умножение (деление) обеих частей неравенства
на положительное число;
3. Применение правил умножения многочленов и
формул сокращённого умножения;
4. Приведение подобных членов многочлена;
5. Возведение неравенства в нечётную степень;
f ( x)
6. Логарифмирование неравенства
a
>a
т.е замена этого неравенства неравенством
g ( x)
f ( x) > g( x) при a> 1 или f ( x) < g( x) при 0< a< 1
9.
Равносильность неравенствна некотором множестве чисел
1.Возведение неравенства в чётную
степень;
2.Потенцирование неравенства;
3. Умножение обеих частей неравенства
на функцию;
4. Применение некоторых формул
(логарифмических,
тригонометрических и др.)
10.
Равносильны ли неравенства?2
x ≥9 ( x−3) ( x+ 3) > 0
2
x > x x> 1
log3( 2− x) > log3 x 2− x> x
2
x −1
≥0
x−1
x≥−1
11.
Методы решения неравенствалгебраический
функциональный
графический
геометрический
12.
Алгебраические методырешения неравенств
Сведение неравенства к равносильной
системе или совокупности систем
Метод замены
Разбиение области определения
неравенства на подмножества
13.
Сведение неравенства к равносильнойсовокупности систем неравенств
logϕ( x) f ( x) ≥logϕ( x) g( x) ⇔
[ f ( x) ≥g( x) >0¿ ¿¿¿¿
{¿
14.
Решите logнеравенство
(
42 x − 13 x +
2
3 x
3 x > 1¿ {
{
¿
1)
42 x 2− 13 x +
Решение
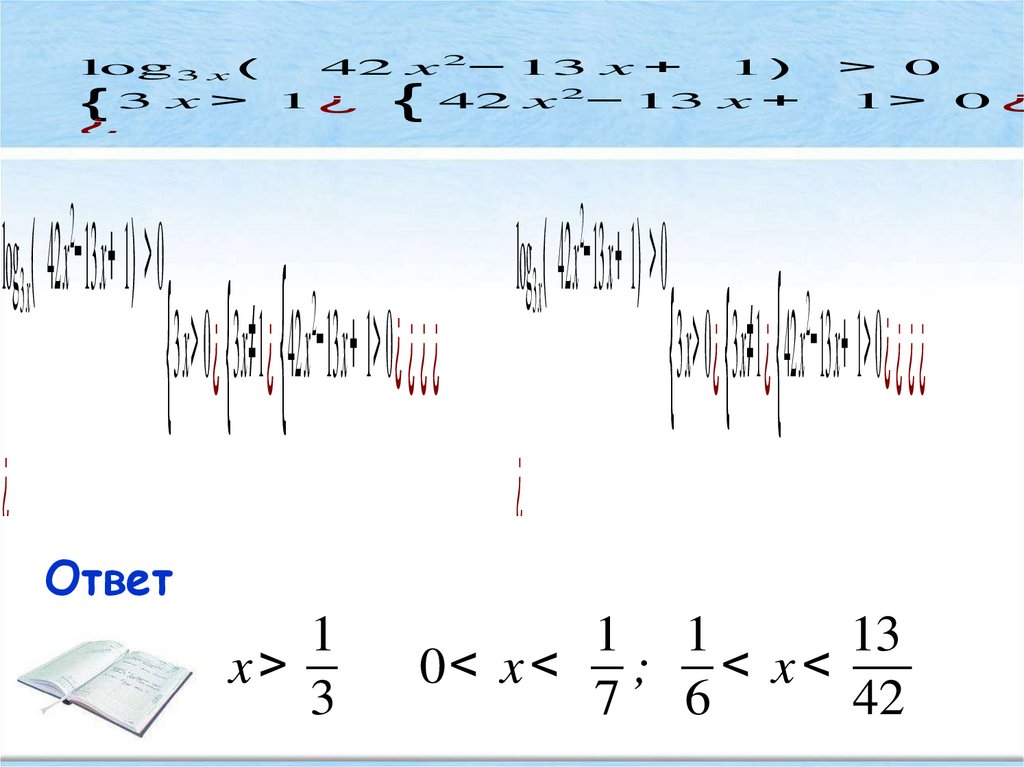
log3 x ( 42 x −13 x+ 1) > 0
¿
2
¿
3
x>
1¿
42
x
−13
x+
1>
0
¿¿
{¿
2
{
>
1>
15.
{{1
1
1
x> ¿ 42 ( x− ) ⋅( x− ) > 0 ¿ ¿ ¿ ¿
3
6
7
{ {
1
1 1
x> ¿ x< , x> ¿ ¿ ¿ ¿
3
7 6
1
x>
3
1 1
13
0< x < ; < x <
7 6
42
16.
Квант №10 1990 г.“Некоторые полезные логарифмические
соотношения”
Если
Аналогично можно доказать , что если
17.
log 3 x (42 x 2− 13 x +
1)
3 x > 1¿
42 x 2− 13 x +
{
¿
> 0
1> 0 ¿
{
log3x( 42x −13x+ 1) >0
2
log3x( 42x −13x+ 1) >0
2
{{{
3x> 0¿ 3x≠1¿ 42x −13x+ 1> 0¿ ¿¿¿
2
¿
{{{
3x> 0¿ 3x≠1¿ 42x −13x+ 1> 0¿ ¿¿¿
2
¿
Ответ
1
x>
3
1 1
13
0< x < ; < x <
7 6
42
18.
Решите неравенство2
log2 x+ 3 x < 1
Решение.
2
log2 x+ 3 x −1< 0
{ {{
( 2x+ 3−1) ( x −2x−3) <0¿ 2x+ 3>0¿ 2x+ 3≠1¿ ¿
2
19.
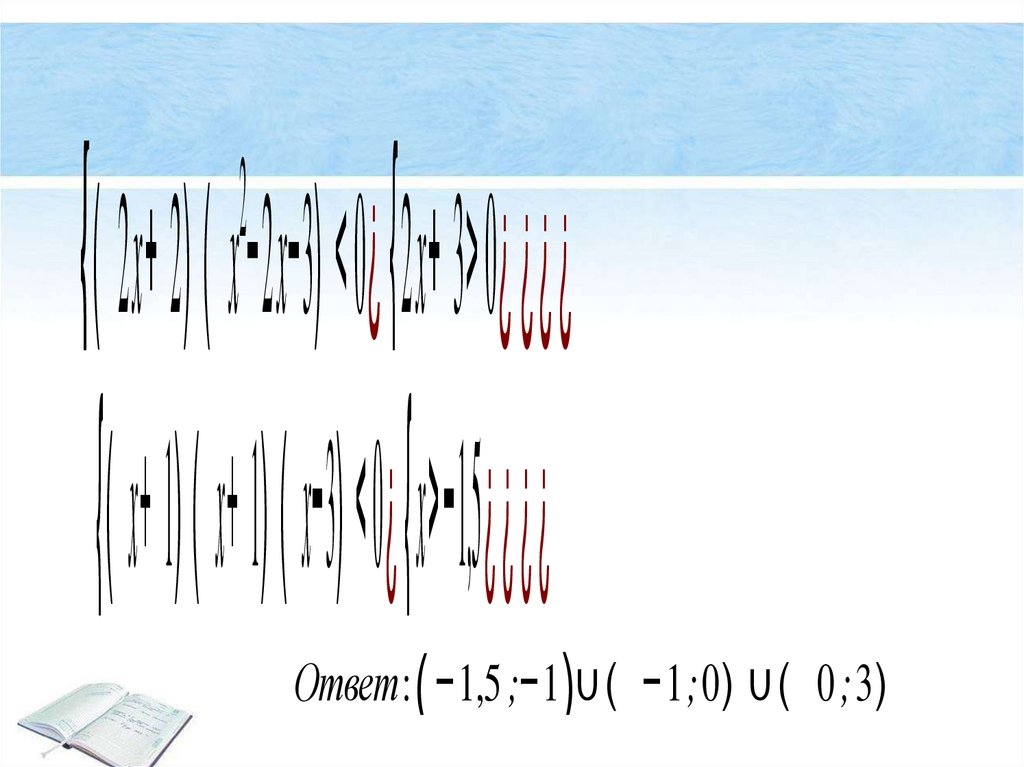
{ {( 2x+ 2) ( x −2x−3) <0¿ 2x+ 3> 0¿ ¿¿¿
2
{
( x+ 1) ( x+ 1) ( x−3) < 0¿ x>−1,5¿ ¿
{
Ответ: ( −1,5 ;−1 )∪ ( −1;0) ∪ ( 0 ;3)


















 Математика
Математика








