Похожие презентации:
Определение точки пересечения двух отрезков
1.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯОПРЕДЕЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ОТРЕЗКОВ
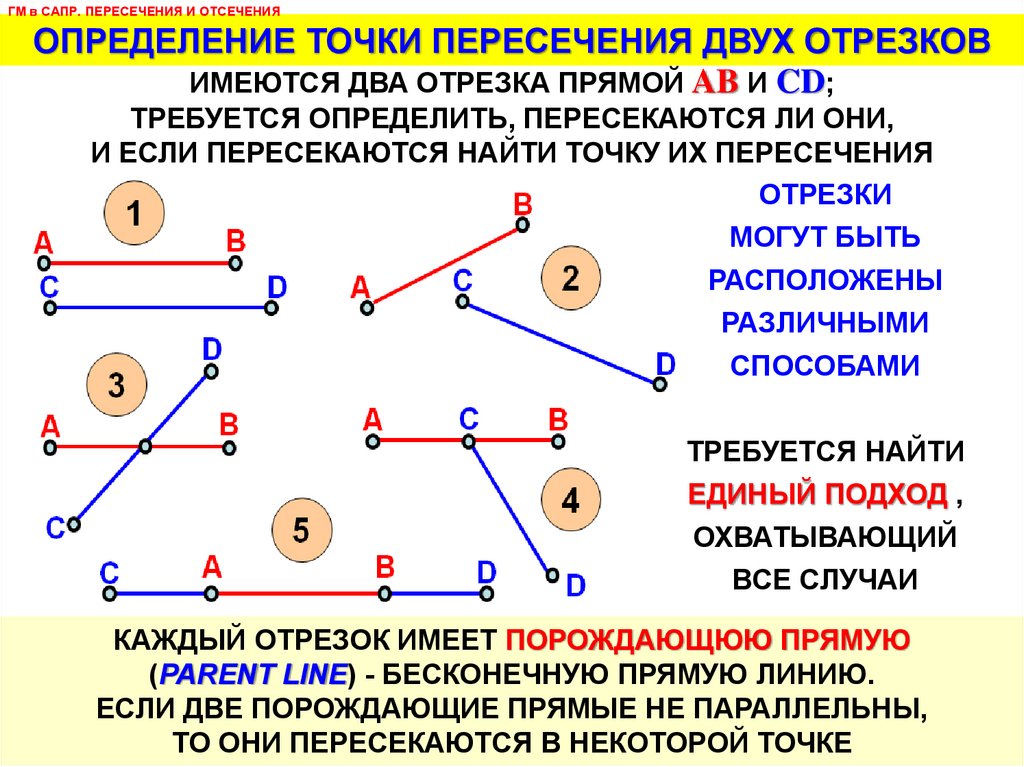
ИМЕЮТСЯ ДВА ОТРЕЗКА ПРЯМОЙ AB И CD;
ТРЕБУЕТСЯ ОПРЕДЕЛИТЬ, ПЕРЕСЕКАЮТСЯ ЛИ ОНИ,
И ЕСЛИ ПЕРЕСЕКАЮТСЯ НАЙТИ ТОЧКУ ИХ ПЕРЕСЕЧЕНИЯ
ОТРЕЗКИ
МОГУТ БЫТЬ
РАСПОЛОЖЕНЫ
РАЗЛИЧНЫМИ
СПОСОБАМИ
ТРЕБУЕТСЯ НАЙТИ
ЕДИНЫЙ ПОДХОД ,
ОХВАТЫВАЮЩИЙ
ВСЕ СЛУЧАИ
КАЖДЫЙ ОТРЕЗОК ИМЕЕТ ПОРОЖДАЮЩЮЮ ПРЯМУЮ
(PARENT LINE) - БЕСКОНЕЧНУЮ ПРЯМУЮ ЛИНИЮ.
ЕСЛИ ДВЕ ПОРОЖДАЮЩИЕ ПРЯМЫЕ НЕ ПАРАЛЛЕЛЬНЫ,
ТО ОНИ ПЕРЕСЕКАЮТСЯ В НЕКОТОРОЙ ТОЧКЕ
2.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВВЕДЕМ ПАРАМЕТРИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ
ДЛЯ ПОРОЖДАЮЩИХ ПРЯМЫХ ЗАДАННЫХ ОТРЕЗКОВ
AB(t ) A b t CD (u ) C d u
t ,
ГДЕ
b B A d D C u ,
В ОБЩЕЙ ТОЧКЕ ЗНАЧЕНИЯ ПАРАМЕТРИЧЕСКИХ УРАВНЕНИЙ
ПОРОЖДАЮЩИХ ПРЯМЫХ ДОЛЖНЫ СОВПАДАТЬ
A b t С d u
ВВЕДЕМ ВЕКТОР c (C A) ТОГДА
b t (С A) d u c d u (1)
3.
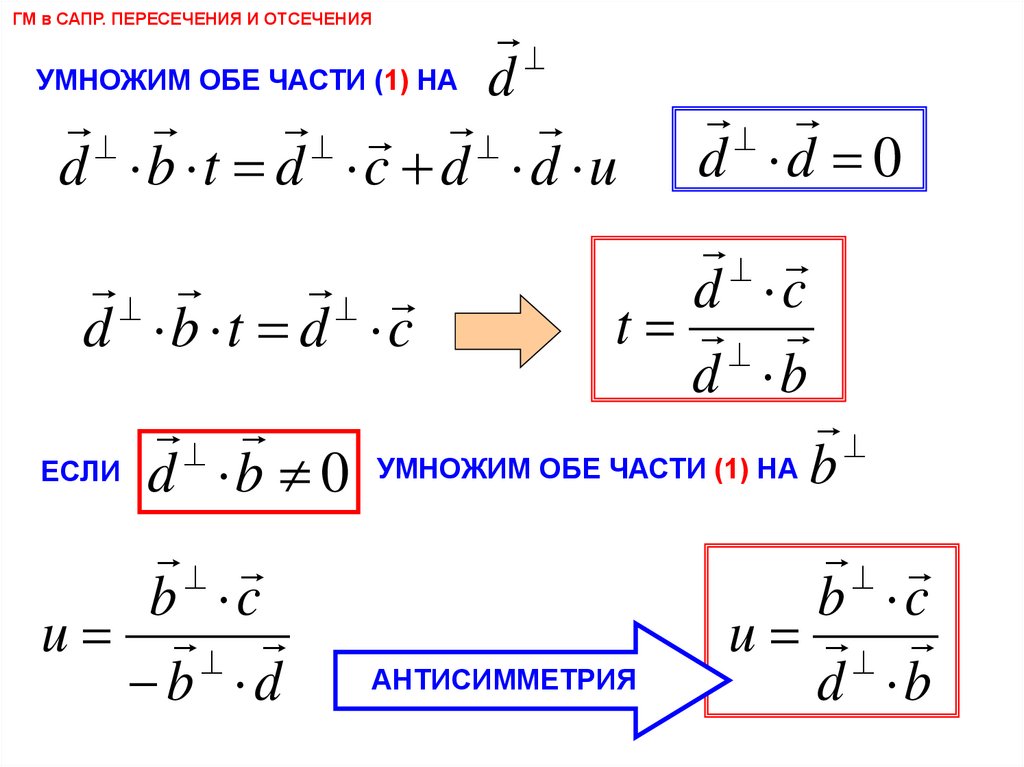
УМНОЖИМ ОБЕ ЧАСТИ (1) НА dd b t d c d d u
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ
d d 0
d c
t
d b t d c
d b
ЕСЛИ d b 0 УМНОЖИМ ОБЕ ЧАСТИ (1) НА b
b c
b c
u
u
АНТИСИММЕТРИЯ
b d
d b
4.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯЕСЛИ d b 0
ТО ДВЕ ПОРОЖДАЮЩИЕ ПРЯМЫЕ ПЕРЕСЕКАЮТСЯ,
НО ЭТО НЕ ОЗНАЧАЕТ, ЧТО ПЕРЕСЕКАЮТСЯ
ЗАДАННЫЕ ОТРЕЗКИ ЭТИХ ПРЯМЫХ
t 0, 1 u 0, 1
d c
b c
E A b C d
d b
d b
ЕСЛИ d b 0
ТО ВЕКТОРЫ b И d ПАРАЛЛЕЛЬНЫ
5.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИМЕР
ЗАДАНЫ ЧЕТЫРЕ ТОЧКИ НА ПЛОСКОСТИ
A = (0, 6), В = (6, 1), C=(1,3), D=(5,5)
НЕОБХОДИМО НАЙТИ ТОЧКУ ПЕРЕСЕЧЕНИЯ
ОТРЕЗКОВ AB И CD, ЕСЛИ ТАКОВАЯ СУЩЕСТВУЕТ
ВВЕДЕМ ВЕКТОРЫ
d D C
b B A
c C A
d (5 1, 5 3) (4 , 2)
b (6 0 , 1 6) (6 , 5)
c (1 0 , 3 6) (1, 3)
d c
t
d b
b c
u
d b
6.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВЫЧИСЛИМ ЗНАЧЕНИЕ ЗНАМЕНАТЕЛЯ
d b d x by d y bx 4 ( 5) 2 6 32 0
ЗНАЧЕНИЕ ЧИСЛИТЕЛЯ
d c d x c y d y cx 4 ( 3) 2 1 14
d c 14 7 Т.Е.
t 0, 1
ТОГДА t
d b 32 16
ОПРЕДЕЛИМ ЗНАЧЕНИЕ ЧИСЛИТЕЛЯ ДЛЯ ПАРАМЕТРА
u
b c bx c y by cx 6 ( 3) ( 5) 1 13
7.
b c 13 13ТОГДА u
d b 32 32
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ
u 0, 1
КООРДИНАТЫ (X,Y) ТОЧКИ ПЕРЕСЕЧЕНИЯ ДЛЯ ОТРЕЗКА AB
b B A (6 ; 5) ;
AB(t ) A b t (0 6t ; 6 5t ) .
7
ПРИ t
ЗНАЧЕНИЯ КООРДИНАТ ТОЧКИ ПЕРЕСЕЧЕНИЯ:
16
6 7 21
5
5 7 61 13
x
2
y 6
3
16
8
8
16 16
16
8.
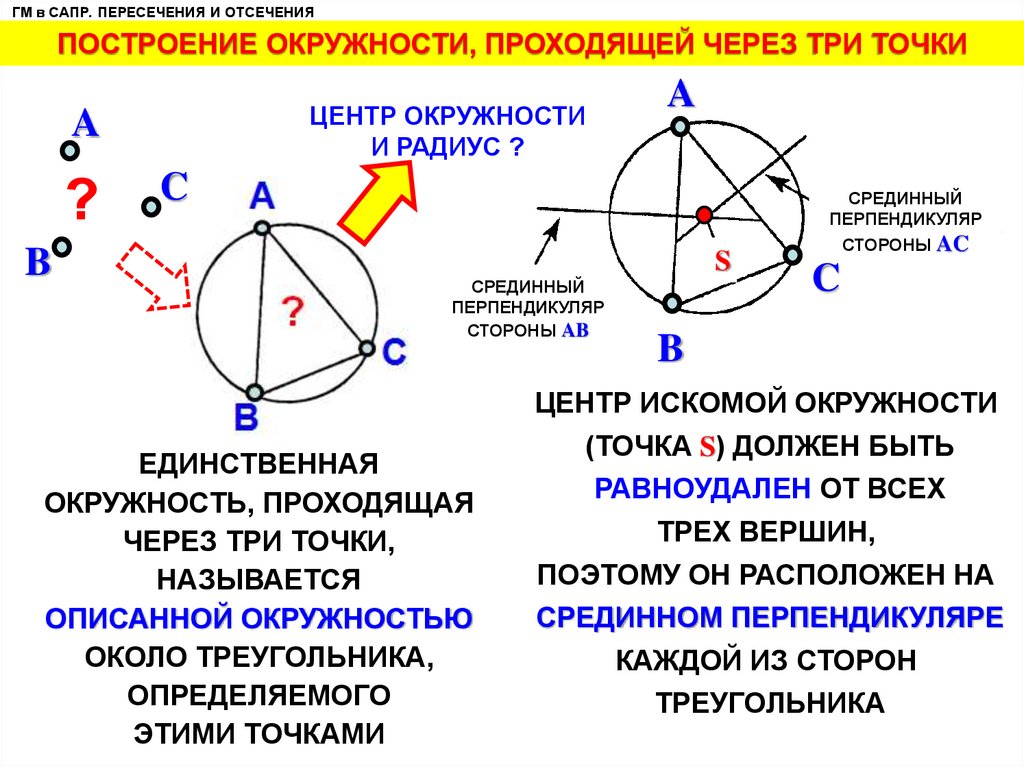
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПОСТРОЕНИЕ ОКРУЖНОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТРИ ТОЧКИ
A ЦЕНТР ОКРУЖНОСТИ
A
?
A
И РАДИУС ?
C
СРЕДИННЫЙ
ПЕРПЕНДИКУЛЯР
?
C
B
B
S
СРЕДИННЫЙ
ПЕРПЕНДИКУЛЯР
СТОРОНЫ AB
ЕДИНСТВЕННАЯ
ОКРУЖНОСТЬ, ПРОХОДЯЩАЯ
ЧЕРЕЗ ТРИ ТОЧКИ,
НАЗЫВАЕТСЯ
ОПИСАННОЙ ОКРУЖНОСТЬЮ
ОКОЛО ТРЕУГОЛЬНИКА,
ОПРЕДЕЛЯЕМОГО
ЭТИМИ ТОЧКАМИ
СТОРОНЫ AC
C
B
ЦЕНТР ИСКОМОЙ ОКРУЖНОСТИ
(ТОЧКА S) ДОЛЖЕН БЫТЬ
РАВНОУДАЛЕН ОТ ВСЕХ
ТРЕХ ВЕРШИН,
ПОЭТОМУ ОН РАСПОЛОЖЕН НА
СРЕДИННОМ ПЕРПЕНДИКУЛЯРЕ
КАЖДОЙ ИЗ СТОРОН
ТРЕУГОЛЬНИКА
9.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ90 0
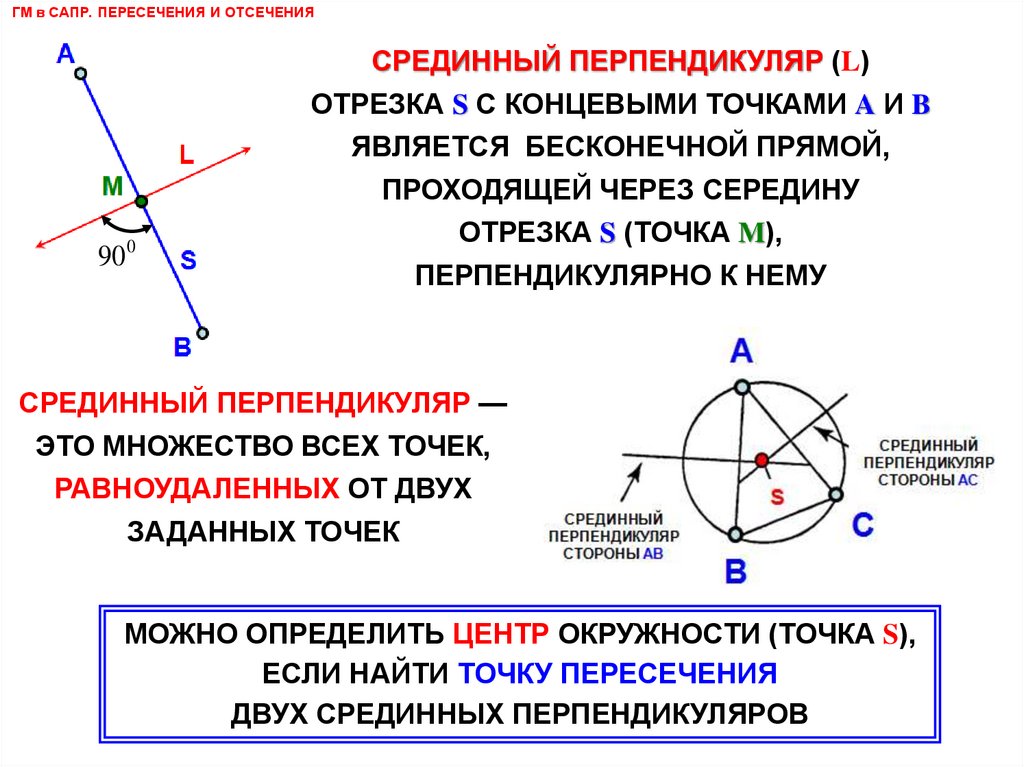
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР (L)
ОТРЕЗКА S С КОНЦЕВЫМИ ТОЧКАМИ A И B
ЯВЛЯЕТСЯ БЕСКОНЕЧНОЙ ПРЯМОЙ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ СЕРЕДИНУ
ОТРЕЗКА S (ТОЧКА M),
ПЕРПЕНДИКУЛЯРНО К НЕМУ
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР —
ЭТО МНОЖЕСТВО ВСЕХ ТОЧЕК,
РАВНОУДАЛЕННЫХ ОТ ДВУХ
ЗАДАННЫХ ТОЧЕК
МОЖНО ОПРЕДЕЛИТЬ ЦЕНТР ОКРУЖНОСТИ (ТОЧКА S),
ЕСЛИ НАЙТИ ТОЧКУ ПЕРЕСЕЧЕНИЯ
ДВУХ СРЕДИННЫХ ПЕРПЕНДИКУЛЯРОВ
10.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯУРАВНЕНИЕ СРЕДИННОГО ПЕРПЕНДИКУЛЯРА
A
a
c N
r
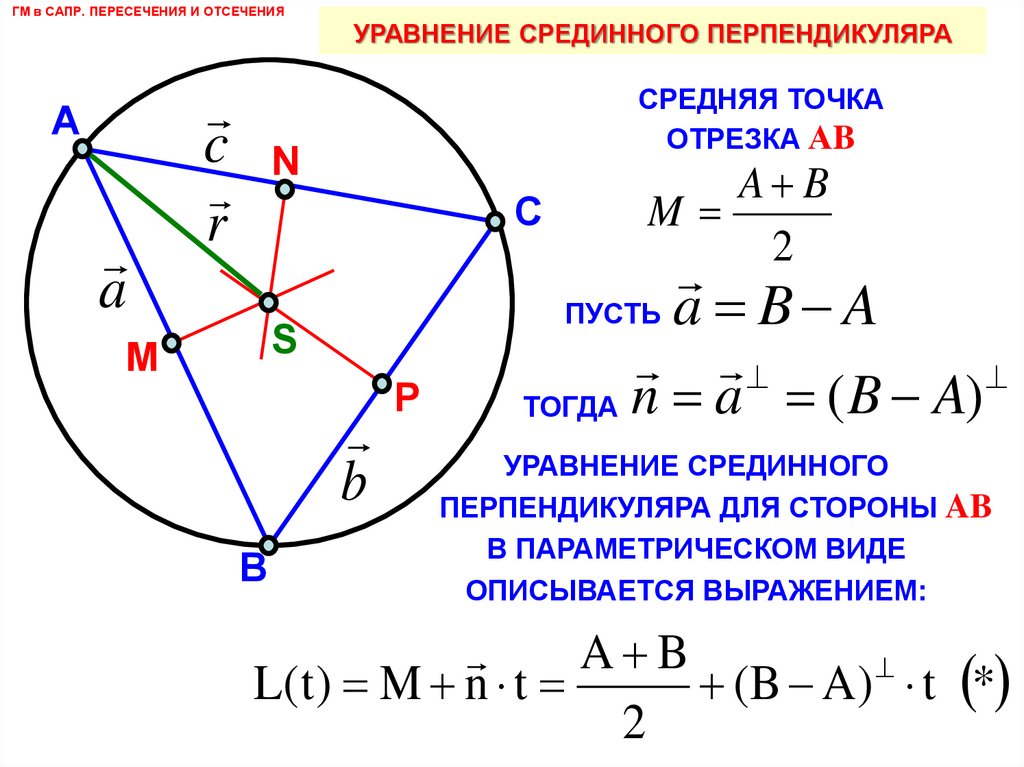
СРЕДНЯЯ ТОЧКА
ОТРЕЗКА АB
C
S
M
b
B
P
A B
M
2
ПУСТЬ a B A
( B A)
ТОГДА n a
УРАВНЕНИЕ СРЕДИННОГО
ПЕРПЕНДИКУЛЯРА ДЛЯ СТОРОНЫ AB
В ПАРАМЕТРИЧЕСКОМ ВИДЕ
ОПИСЫВАЕТСЯ ВЫРАЖЕНИЕМ:
A B
L( t ) M n t
(B A) t *
2
11.
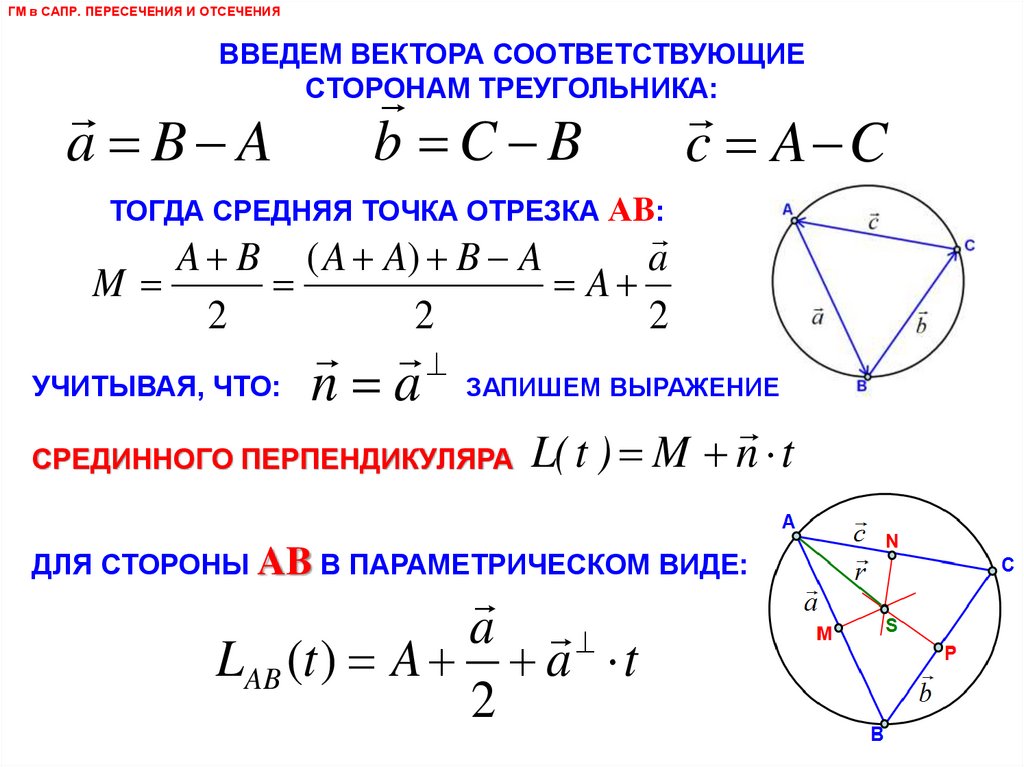
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВВЕДЕМ ВЕКТОРА СООТВЕТСТВУЮЩИЕ
СТОРОНАМ ТРЕУГОЛЬНИКА:
a B A
b C B
c A C
ТОГДА СРЕДНЯЯ ТОЧКА ОТРЕЗКА АB:
A B ( A A) B A
a
M
A
2
2
2
УЧИТЫВАЯ, ЧТО: n a
ЗАПИШЕМ ВЫРАЖЕНИЕ
СРЕДИННОГО ПЕРПЕНДИКУЛЯРА L( t ) M n t
ДЛЯ СТОРОНЫ AB В ПАРАМЕТРИЧЕСКОМ ВИДЕ:
a
LAB (t ) A a t
2
12.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯАНАЛОГИЧНО НАЙДЁМ СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
c
ДЛЯ СТОРОНЫ AС: L AC (u ) A
c u
2
ТАК КАК ТОЧКА S ЯВЛЯЕТСЯ ТОЧКОЙ ПЕРЕСЕЧЕНИЯ
ДВУХ СРЕДИННЫХ ПЕРПЕНДИКУЛЯРОВ ТО: L AB (t ) L AC (u )
a
c
A a t A c u
2
2
УЧИТЫВАЯ, ЧТО: a B A
b C B c A C
a b c 0
a c b
a
c
a t c u
2
2
a c
a t c u
2
b
a t c u
2
13.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯu
ИСКЛЮЧИМ ИЗ ПОЛУЧЕННОГО ВЫРАЖЕНИЯ ПАРАМЕТР
b
c a t c c c u
2
1 b c
t
2 a c
t
ПОДСТАВИМ ПОЛУЧЕННОЕ ЗНАЧЕНИЕ ПАРАМЕТРА
В УРАВНЕНИЕ ПРЯМОЙ (СРЕДИННОГО ПЕРПЕНДИКУЛЯРА)
ДЛЯ ПОЛУЧЕНИЯ КООРДИНАТ ТОЧКИ S:
a
a a b c
S A a t A
2
2 2 a c
1 b c
A a a
2
a c
14.
1 b c ЦЕНТР ОПИСАННОЙS A a a ОКРУЖНОСТИ
2
a c
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ
РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ РАВЕН РАССТОЯНИЮ
ОТ ТОЧКИ S ДО ЛЮБОЙ ИЗ ТРЕХ ВЕРШИН, НАПРИМЕР A
R S A r
1 b c
r
a
a
РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ
2
a
c
ВЕКТОР r ОПРЕДЕЛЯЕТ
ОПРЕДЕЛИМ R - ДЛИНУ ВЕКТОРА
r
2
a b c
1
R r r r
2 a c
ЗНАЯ КООРДИНАТЫ ЦЕНТРА (ТОЧКА S) И РАДИУС R МОЖНО
ВЫПОЛНИТЬ ПОСТРОЕНИЕ ОКРУЖНОСТИ
15.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИМЕР
НАЙТИ ПАРАМЕТРИЧЕСКУЮ ФОРМУ СРЕДИННОГО
ПЕРПЕНДИКУЛЯРА L(t) ДЛЯ ОТРЕЗКА S, ИМЕЮЩЕГО
КОНЦЕВЫЕ ТОЧКИ:
A = (3, 5) И В = (9, 3)
16.
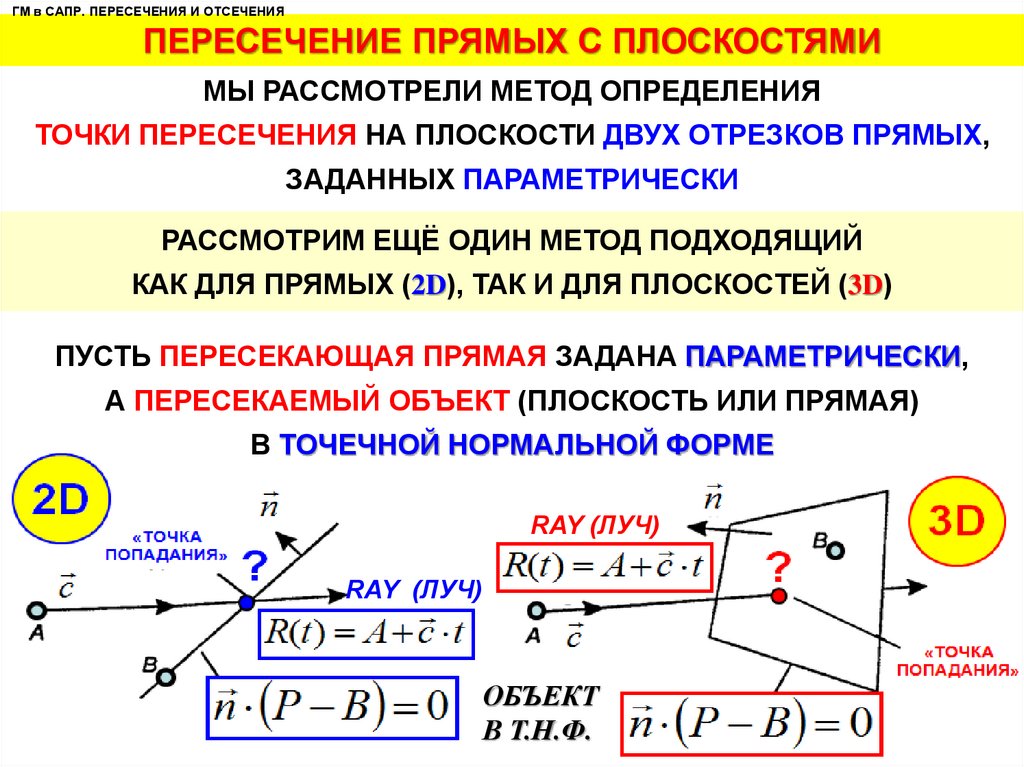
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПЕРЕСЕЧЕНИЕ ПРЯМЫХ С ПЛОСКОСТЯМИ
МЫ РАССМОТРЕЛИ МЕТОД ОПРЕДЕЛЕНИЯ
ТОЧКИ ПЕРЕСЕЧЕНИЯ НА ПЛОСКОСТИ ДВУХ ОТРЕЗКОВ ПРЯМЫХ,
ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
РАССМОТРИМ ЕЩЁ ОДИН МЕТОД ПОДХОДЯЩИЙ
КАК ДЛЯ ПРЯМЫХ (2D), ТАК И ДЛЯ ПЛОСКОСТЕЙ (3D)
ПУСТЬ ПЕРЕСЕКАЮЩАЯ ПРЯМАЯ ЗАДАНА ПАРАМЕТРИЧЕСКИ,
А ПЕРЕСЕКАЕМЫЙ ОБЪЕКТ (ПЛОСКОСТЬ ИЛИ ПРЯМАЯ)
В ТОЧЕЧНОЙ НОРМАЛЬНОЙ ФОРМЕ
RAY (ЛУЧ)
RAY (ЛУЧ)
ОБЪЕКТ
В Т.Н.Ф.
17.
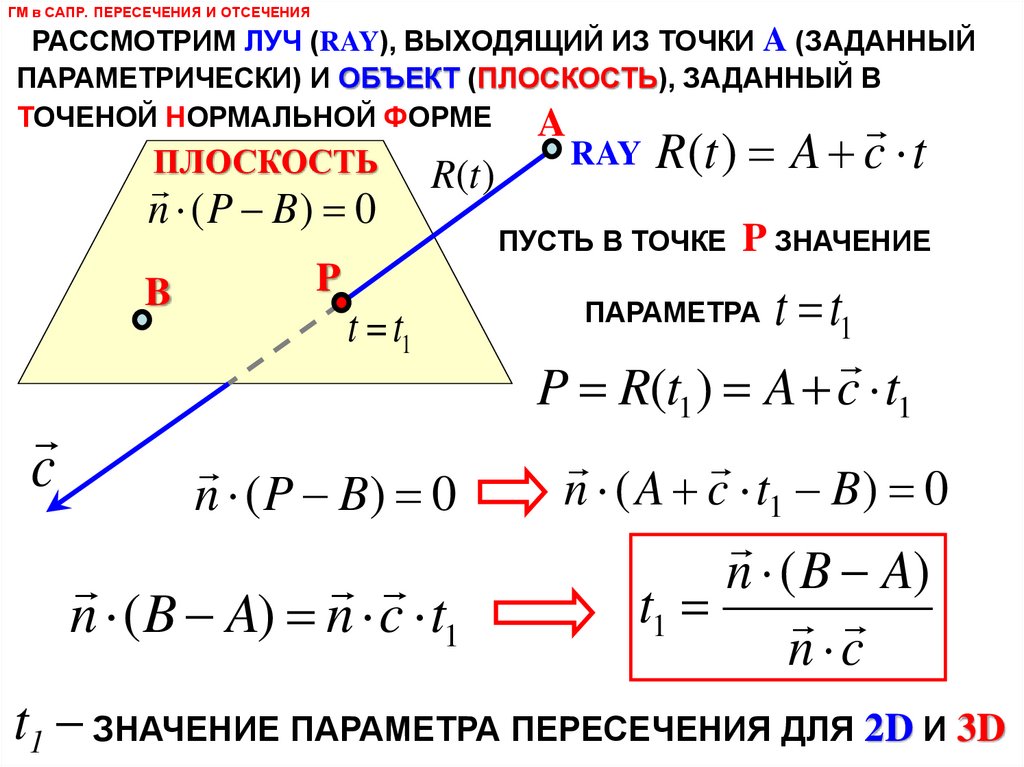
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯРАССМОТРИМ ЛУЧ (RAY), ВЫХОДЯЩИЙ ИЗ ТОЧКИ A (ЗАДАННЫЙ
ПАРАМЕТРИЧЕСКИ) И ОБЪЕКТ (ПЛОСКОСТЬ), ЗАДАННЫЙ В
ТОЧЕНОЙ НОРМАЛЬНОЙ ФОРМЕ
A
ПЛОСКОСТЬ
n ( P B) 0
B
c
P
R(t )
t t1
n ( P B) 0
n ( B A) n c t1
RAY R (t ) A c t
ПУСТЬ В ТОЧКЕ P ЗНАЧЕНИЕ
ПАРАМЕТРА
t t1
P R(t1 ) A c t1
n ( A c t1 B) 0
n ( B A)
t1
n c
t1 ЗНАЧЕНИЕ ПАРАМЕТРА ПЕРЕСЕЧЕНИЯ ДЛЯ 2D И 3D
18.
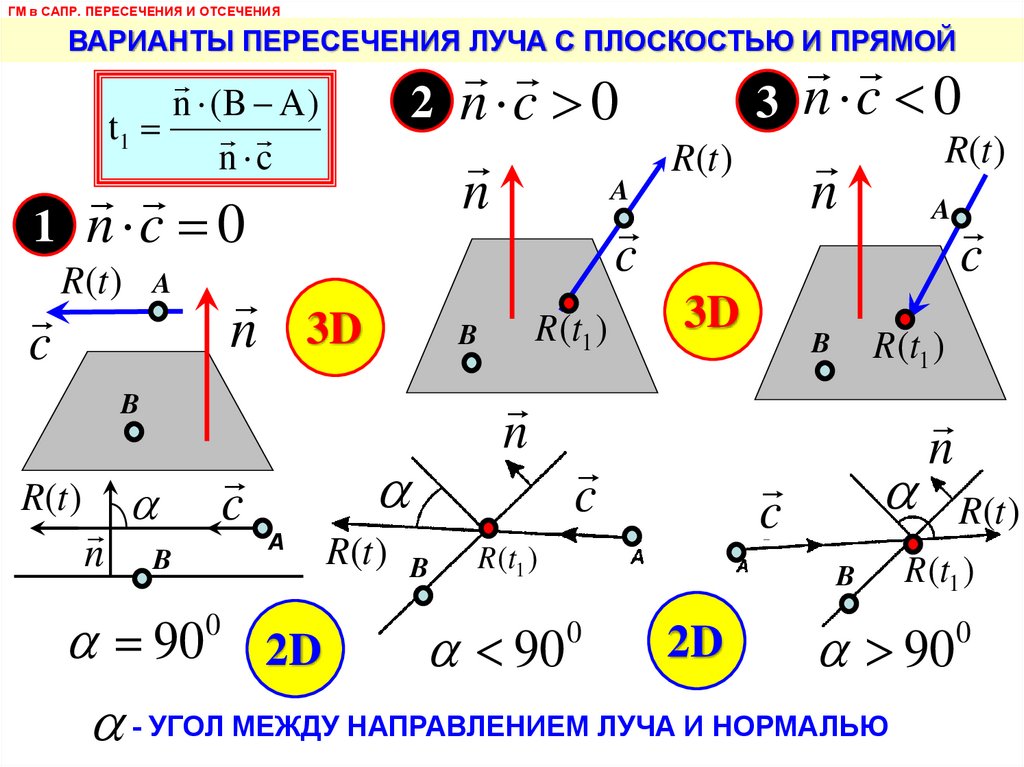
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВАРИАНТЫ ПЕРЕСЕЧЕНИЯ ЛУЧА С ПЛОСКОСТЬЮ И ПРЯМОЙ
2 n c 0
A
n
n (B A)
t1
n c
1 n c 0
R(t ) A
n 3D
c
c
B
R(t )
c
n
B
А
R (t1 )
B
R(t ) B
n
R (t1 )
c
3 n c 0
R(t )
R(t )
n
A
c
3D
R (t1 )
B
c
B
n
R(t )
R (t1 )
0
0
2D
90 2D
90
90
- УГОЛ МЕЖДУ НАПРАВЛЕНИЕМ ЛУЧА И НОРМАЛЬЮ
0
19.
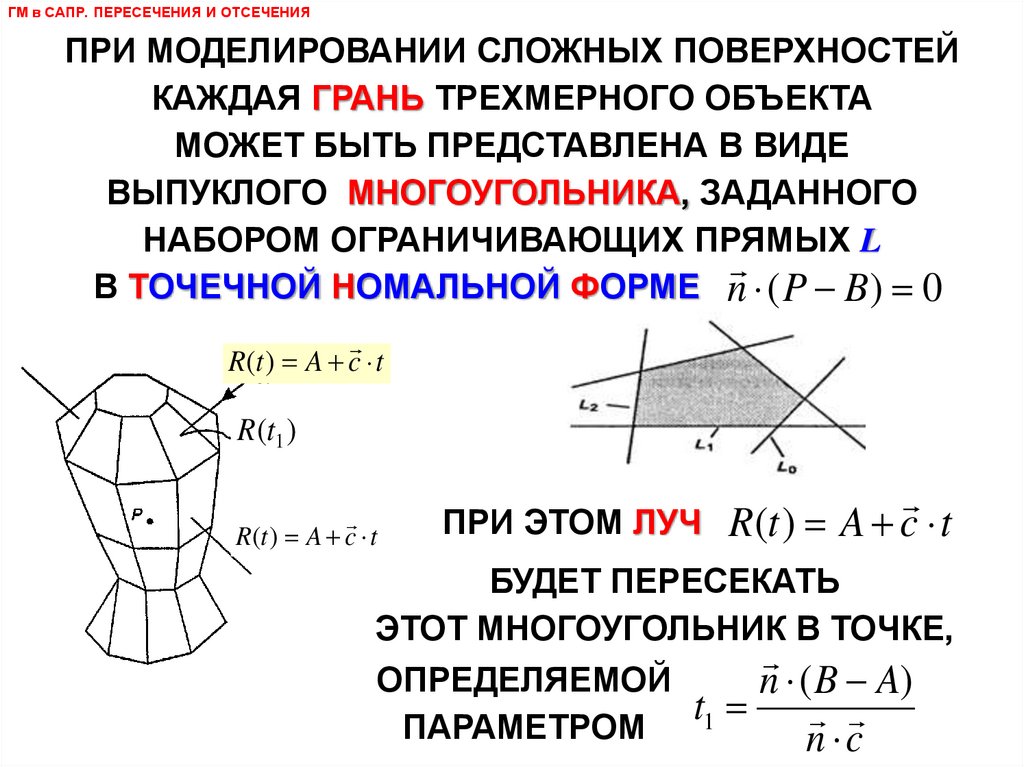
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИ МОДЕЛИРОВАНИИ СЛОЖНЫХ ПОВЕРХНОСТЕЙ
КАЖДАЯ ГРАНЬ ТРЕХМЕРНОГО ОБЪЕКТА
МОЖЕТ БЫТЬ ПРЕДСТАВЛЕНА В ВИДЕ
ВЫПУКЛОГО МНОГОУГОЛЬНИКА, ЗАДАННОГО
НАБОРОМ ОГРАНИЧИВАЮЩИХ ПРЯМЫХ L
В ТОЧЕЧНОЙ НОМАЛЬНОЙ ФОРМЕ n ( P B ) 0
R (t ) A c t
R (t1 )
R (t ) A c t
ПРИ ЭТОМ ЛУЧ R (t ) A c t
БУДЕТ ПЕРЕСЕКАТЬ
ЭТОТ МНОГОУГОЛЬНИК В ТОЧКЕ,
ОПРЕДЕЛЯЕМОЙ
n ( B A)
t1
ПАРАМЕТРОМ
n c
20.
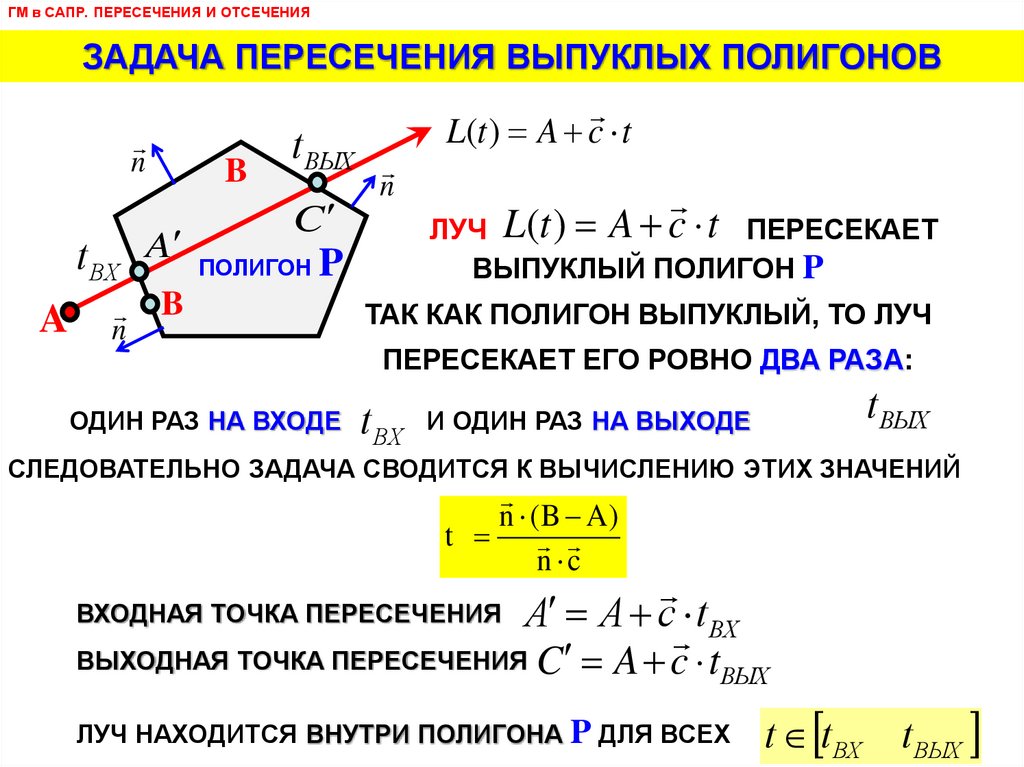
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯЗАДАЧА ПЕРЕСЕЧЕНИЯ ВЫПУКЛЫХ ПОЛИГОНОВ
n
B
t ВЫХ
C
t ВХ A ПОЛИГОН P
A
n
B
ОДИН РАЗ НА ВХОДЕ
n
L(t ) A c t
ЛУЧ L(t ) A c t ПЕРЕСЕКАЕТ
ВЫПУКЛЫЙ ПОЛИГОН P
ТАК КАК ПОЛИГОН ВЫПУКЛЫЙ, ТО ЛУЧ
ПЕРЕСЕКАЕТ ЕГО РОВНО ДВА РАЗА:
t ВЫХ
t ВХ И ОДИН РАЗ НА ВЫХОДЕ
СЛЕДОВАТЕЛЬНО ЗАДАЧА СВОДИТСЯ К ВЫЧИСЛЕНИЮ ЭТИХ ЗНАЧЕНИЙ
n (B A)
t
n c
ВХОДНАЯ ТОЧКА ПЕРЕСЕЧЕНИЯ A A c t
ВХ
ВЫХОДНАЯ ТОЧКА ПЕРЕСЕЧЕНИЯ C A c t
ВЫХ
ЛУЧ НАХОДИТСЯ ВНУТРИ ПОЛИГОНА P ДЛЯ ВСЕХ
t t ВХ
t ВЫХ
21.
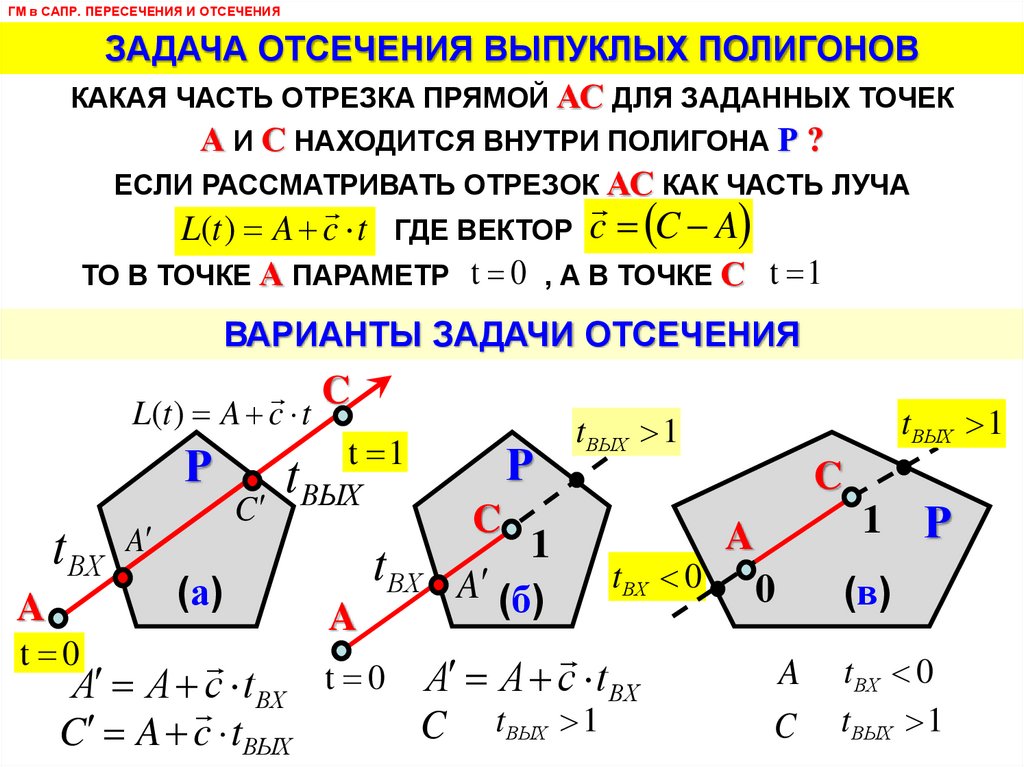
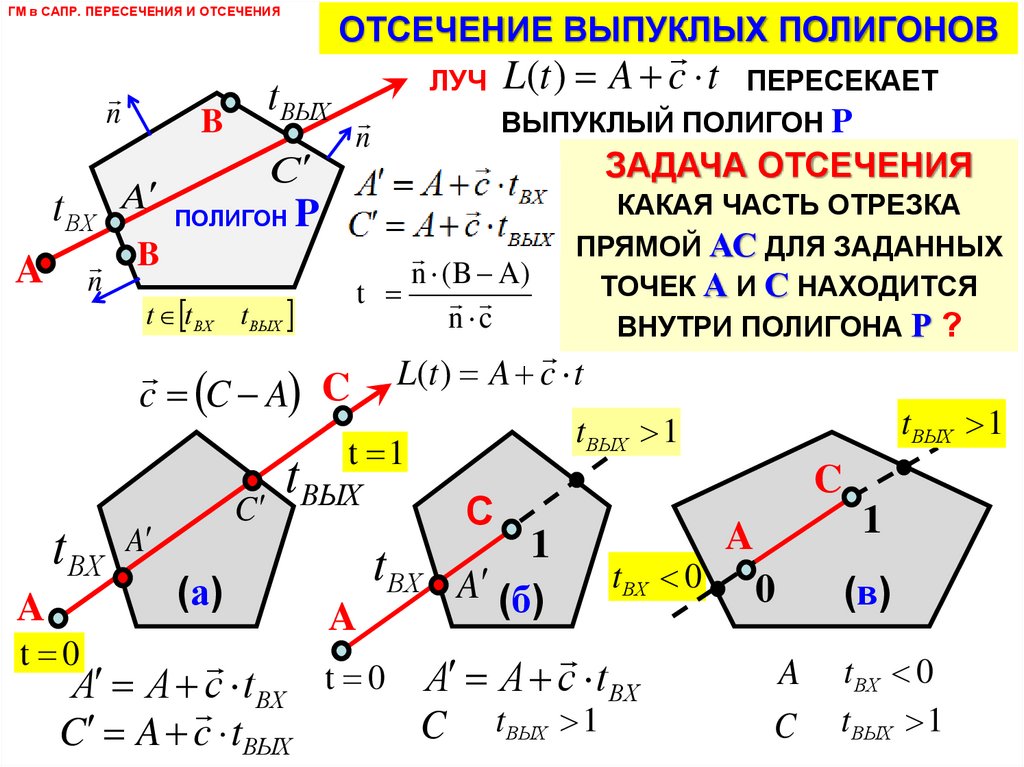
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯЗАДАЧА ОТСЕЧЕНИЯ ВЫПУКЛЫХ ПОЛИГОНОВ
КАКАЯ ЧАСТЬ ОТРЕЗКА ПРЯМОЙ АС ДЛЯ ЗАДАННЫХ ТОЧЕК
А И С НАХОДИТСЯ ВНУТРИ ПОЛИГОНА Р ?
ЕСЛИ РАССМАТРИВАТЬ ОТРЕЗОК АС КАК ЧАСТЬ ЛУЧА
L(t ) A c t ГДЕ ВЕКТОР c C A
ТО В ТОЧКЕ А ПАРАМЕТР t 0 , А В ТОЧКЕ С t 1
ВАРИАНТЫ ЗАДАЧИ ОТСЕЧЕНИЯ
C
L(t ) A c t
t 1
Р
t ВХ
A
t 0
C
A
(а)
t ВЫХ
t ВХ
A
Р
C
C
1
A (б)
tВЫХ 1
tВЫХ 1
t ВХ 0
A A c t ВХ t 0 A A c t ВХ
C tВЫХ 1
C A c t ВЫХ
1
A
Р
0
(в)
A
C
t ВХ 0
tВЫХ 1
22.
ГМ в САПР. ПЕРЕСЕЧЕНИЯИ ОТСЕЧЕНИЯ
2
3
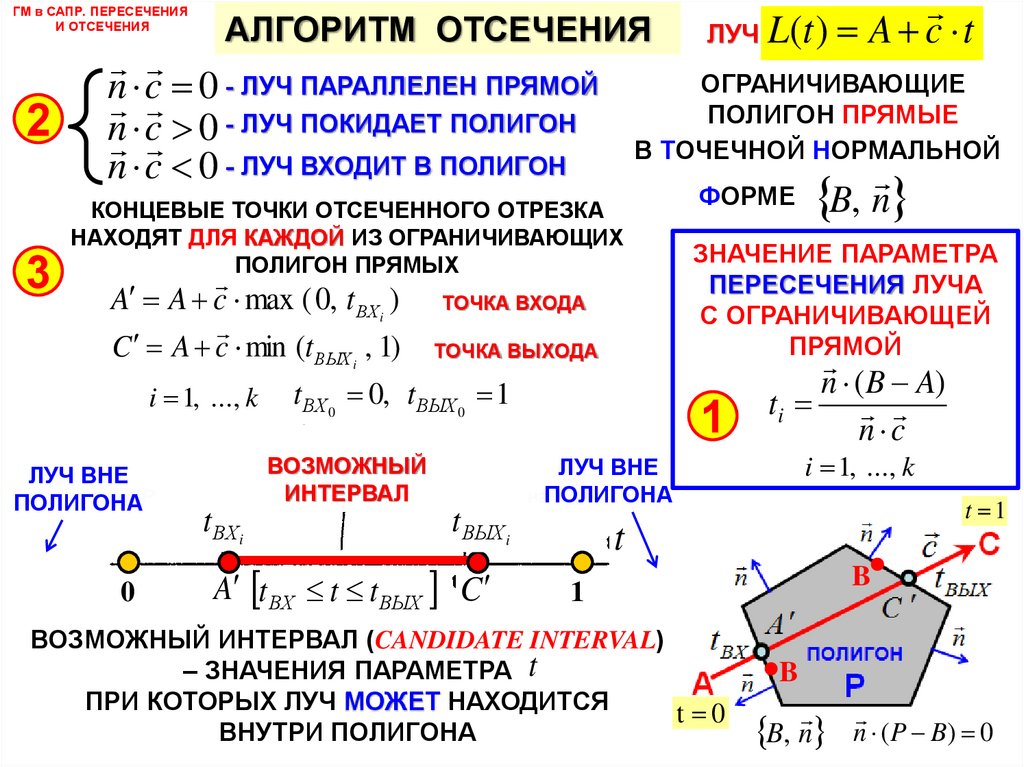
АЛГОРИТМ ОТСЕЧЕНИЯ
n c 0 - ЛУЧ ПАРАЛЛЕЛЕН ПРЯМОЙ
n c 0 - ЛУЧ ПОКИДАЕТ ПОЛИГОН
n c 0 - ЛУЧ ВХОДИТ В ПОЛИГОН
ОГРАНИЧИВАЮЩИЕ
ПОЛИГОН ПРЯМЫЕ
В ТОЧЕЧНОЙ НОРМАЛЬНОЙ
КОНЦЕВЫЕ ТОЧКИ ОТСЕЧЕННОГО ОТРЕЗКА
НАХОДЯТ ДЛЯ КАЖДОЙ ИЗ ОГРАНИЧИВАЮЩИХ
ПОЛИГОН ПРЯМЫХ
A A c max ( 0, t ВХ i ) ТОЧКА ВХОДА
C A c min (t ВЫХ i , 1) ТОЧКА ВЫХОДА
i 1, ..., k t ВХ 0 0, t ВЫХ 0 1
ЛУЧ ВНЕ
ПОЛИГОНА
0
ВОЗМОЖНЫЙ
ИНТЕРВАЛ
t ВХ i
ЛУЧ L(t ) A c t
ФОРМЕ
ЗНАЧЕНИЕ ПАРАМЕТРА
ПЕРЕСЕЧЕНИЯ ЛУЧА
С ОГРАНИЧИВАЮЩЕЙ
ПРЯМОЙ
1
n ( B A)
ti
n c
i 1, ..., k
ЛУЧ ВНЕ
ПОЛИГОНА
t ВЫХ i
A t ВХ t t ВЫХ C
B, n
t 1
t
B
1
ВОЗМОЖНЫЙ ИНТЕРВАЛ (CANDIDATE INTERVAL)
– ЗНАЧЕНИЯ ПАРАМЕТРА t
ПРИ КОТОРЫХ ЛУЧ МОЖЕТ НАХОДИТСЯ
t 0
ВНУТРИ ПОЛИГОНА
B
B, n n (P B) 0
23.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯt ВХ max ( 0, t ВХi )
t ВЫХ min (t ВЫХ i , 1)
ВОЗМОЖНЫЙ ИНТЕРВАЛ
t t ВХ 0 0, t ВЫХ 0 1
n ( B A)
ti
n c
i 1, ..., k
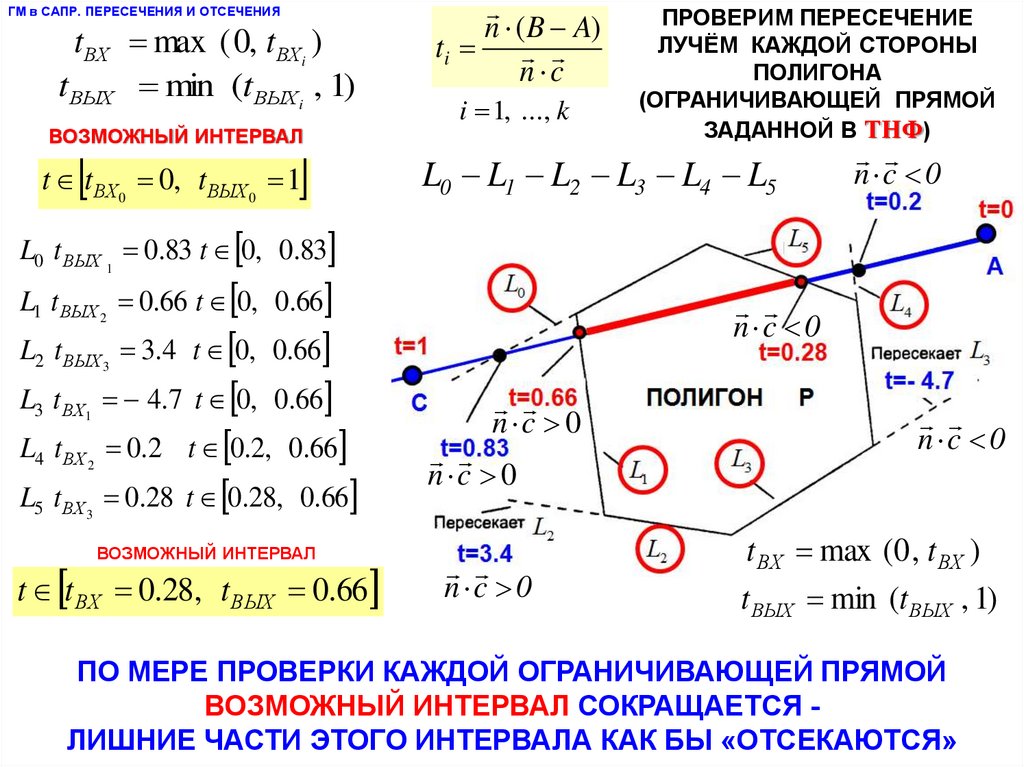
ПРОВЕРИМ ПЕРЕСЕЧЕНИЕ
ЛУЧЁМ КАЖДОЙ СТОРОНЫ
ПОЛИГОНА
(ОГРАНИЧИВАЮЩЕЙ ПРЯМОЙ
ЗАДАННОЙ В ТНФ)
L0 L1 L2 L3 L4 L5
n c 0
L0 t ВЫХ 1 0.83 t 0, 0.83
L1 t ВЫХ 2 0.66 t 0, 0.66
n c 0
L2 t ВЫХ 3 3.4 t 0, 0.66
L3 t ВХ1 4.7 t 0, 0.66
L4 t ВХ 2 0.2 t 0.2, 0.66
L5 t ВХ 3 0.28 t 0.28, 0.66
ВОЗМОЖНЫЙ ИНТЕРВАЛ
t t ВХ 0.28, t ВЫХ 0.66
n c 0
n c 0
n c 0
n c 0
t ВХ max (0 , t ВХ )
t ВЫХ min (t ВЫХ , 1)
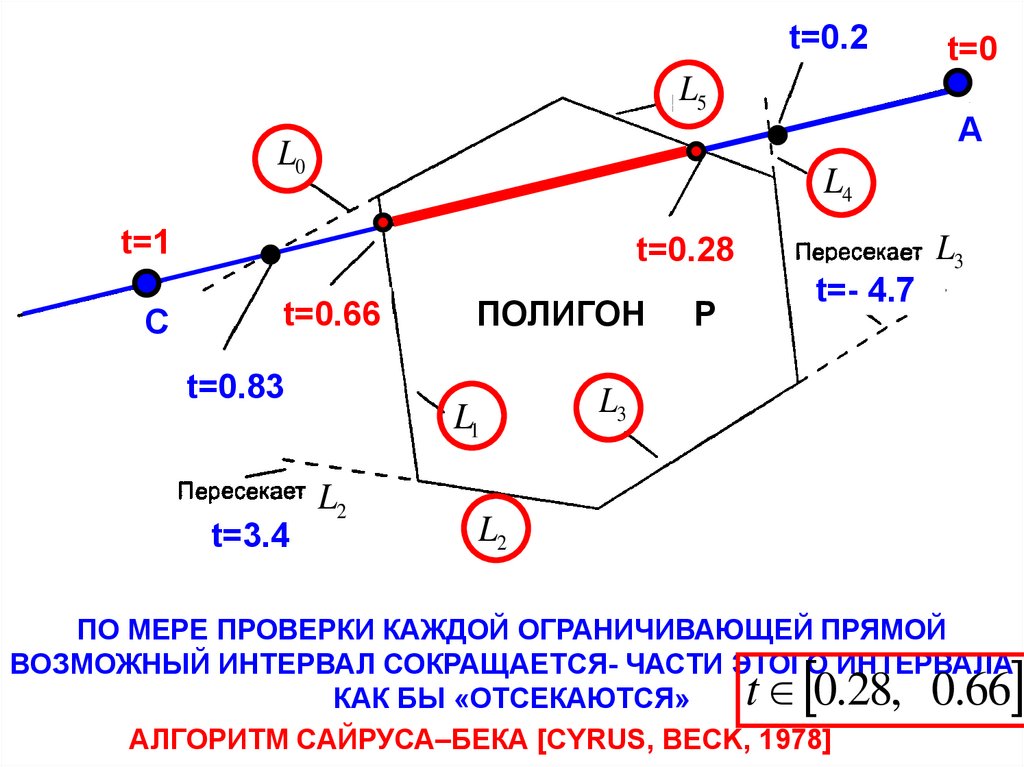
ПО МЕРЕ ПРОВЕРКИ КАЖДОЙ ОГРАНИЧИВАЮЩЕЙ ПРЯМОЙ
ВОЗМОЖНЫЙ ИНТЕРВАЛ СОКРАЩАЕТСЯ ЛИШНИЕ ЧАСТИ ЭТОГО ИНТЕРВАЛА КАК БЫ «ОТСЕКАЮТСЯ»
24.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯАЛГОРИТМ САЙРУСА–БЕКА [CYRUS, BECK, 1978]
1) ПРИСВОИТЬ t ВХ 0, t ВЫХ 1
2) ДЛЯ КАЖДОЙ СТОРОНЫ МНОГОУГОЛЬНИКА ВЫПОЛНИТЬ
СЛЕДУЮЩИЕ ДЕЙСТВИЯ:
a) ЕСЛИ ПОЛУЧЕННОЕ t i ПЕРЕСЕЧЕНИЕ НА ВХОДЕ ( n c 0),
ТО ОПРЕДЕЛИТЬ
t ВХ max ( t ВХ , ti );
b) ЕСЛИ t i ПЕРЕСЕЧЕНИЕ НА ВЫХОДЕ (n c 0),
ТО ОПРЕДЕЛИТЬ
t ВЫХ min (t ВЫХ , ti )
3) ЕСЛИ ДЛЯ КАКОЙ-ЛИБО ИЗ СТОРОН
t ВХ t ВЫХ
ТО ЛУЧ НЕ ПЕРЕСЕКАЕТ ДАННУЮ ПЛОСКУЮ ГРАНЬ;
4) ЕСЛИ ОТСЕЧЕНИЕ НЕ ПУСТОЕ, ТО ПО ФОРМУЛАМ
A A c max ( 0, t ВХ )
B A c min ( t ВХ , 1)
ВЫЧИСЛИТЬ КООРДИНАТЫ КОНЦЕВЫХ ТОЧЕК ОТСЕЧЁННОГО ОТРЕЗКА
25.
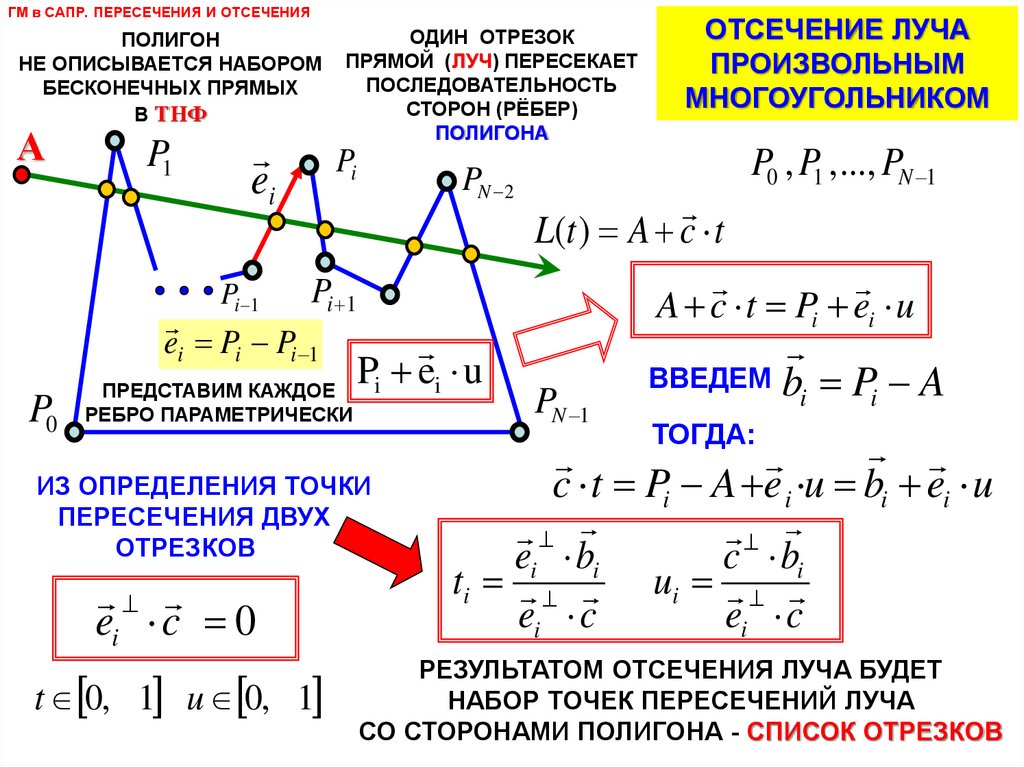
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПОЛИГОН
НЕ ОПИСЫВАЕТСЯ НАБОРОМ
БЕСКОНЕЧНЫХ ПРЯМЫХ
В ТНФ
А
P1
ОДИН ОТРЕЗОК
ПРЯМОЙ (ЛУЧ) ПЕРЕСЕКАЕТ
ПОСЛЕДОВАТЕЛЬНОСТЬ
СТОРОН (РЁБЕР)
ПОЛИГОНА
ei
Pi
Pi 1
Pi 1
PN 2
ei Pi Pi 1
Pi ei u
ПРЕДСТАВИМ КАЖДОЕ
P0 РЕБРО ПАРАМЕТРИЧЕСКИ
ИЗ ОПРЕДЕЛЕНИЯ ТОЧКИ
ПЕРЕСЕЧЕНИЯ ДВУХ
ОТРЕЗКОВ
ei c 0
t 0, 1 u 0, 1
ОТСЕЧЕНИЕ ЛУЧА
ПРОИЗВОЛЬНЫМ
МНОГОУГОЛЬНИКОМ
P0 , P1 , ..., PN 1
L(t ) A c t
A c t Pi ei u
PN 1
ВВЕДЕМ b P A
i
i
ТОГДА:
c t Pi A e i u bi ei u
ei bi
c bi
t i ui
ei c
ei c
РЕЗУЛЬТАТОМ ОТСЕЧЕНИЯ ЛУЧА БУДЕТ
НАБОР ТОЧЕК ПЕРЕСЕЧЕНИЙ ЛУЧА
СО СТОРОНАМИ ПОЛИГОНА - СПИСОК ОТРЕЗКОВ
26.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯЭФФЕКТИВНЫЕ АЛГОРИТМЫ ОТСЕЧЕНИЯ
АЛГОРИТМ КОХЕНА—САЗЕРЛЕНДА (COHEN—SUTHERLAND),
ОТСЕКАЕТ ПРЯМЫЕ СТОРОНАМИ ПРЯМОУГОЛЬНИКА
АЛГОРИТМ САЙРУСА—БЕКА (CYRUS—BECK) ОБОБЩАЕТ
АЛГОРИТМ КОХЕНА—САЗЕРЛЕНДА НА ОТСЕЧЕНИЕ ПРЯМОЙ
ГРАНИЦАМИ ЛЮБОГО ВЫПУКЛОГО МНОГОУГОЛЬНИКА
АЛГОРИТМ САЗЕРЛЕНДА—ХОДЖМЕНА (SUTHERLAND—HODGMAN)
ОТСЕКАЕТ ГРАНИЦАМИ ВЫПУКЛОГО МНОГОУГОЛЬНИКА
ПОЛИГОН, КОТОРЫЙ МОЖЕТ БЫТЬ НЕ ВЫПУКЛЫМ
АЛГОРИТМ ВЕЙЛЕРА—АЗЕРТОНА (WEILER—ATHERTON)
ОТСЕКАЕТ ЛЮБОЙ ПОЛИГОН Р ГРАНИЦАМИ ДРУГОГО
ПОЛИГОНА W, КАК ВЫПУКЛОГО, ТАК И НЕ ВЫПУКЛОГО
27.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯАЛГОРИТМ НАХОЖДЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
ДВЕ ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ ПО ПРЯМОЙ ЛИНИИ.
РАССМОТРИМ ПЛОСКОСТИ, ЗАДАННЫЕ УРАВНЕНИЯМИ:
n ( P A) 0
m ( P B) 0
ОПРЕДЕЛИМ ПАРАМЕТРИЧЕСКУЮ ФОРМУ ПРЯМОЙ
ИХ ПЕРЕСЕЧЕНИЯ
1. ЗАПИШЕМ ОДНУ ИЗ ПЛОСКОСТЕЙ В ПАРАМЕТРИЧЕСКОЙ
ФОРМЕ
P s, t B a s b t
2. ПРИРАВНЯЕМ
n ( P A) B a s b t
3. ВЫРАЗИМ ИЗ ЭТОГО РАВЕНСТВА
НАПРИМЕР -
s КАК ФУНКЦИЮ ОТ t
s E F t
4. ПРЕДСТАВИМ ИСКОМУЮ ПРЯМУЮ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ:
L(t ) B a E F t b t
28.
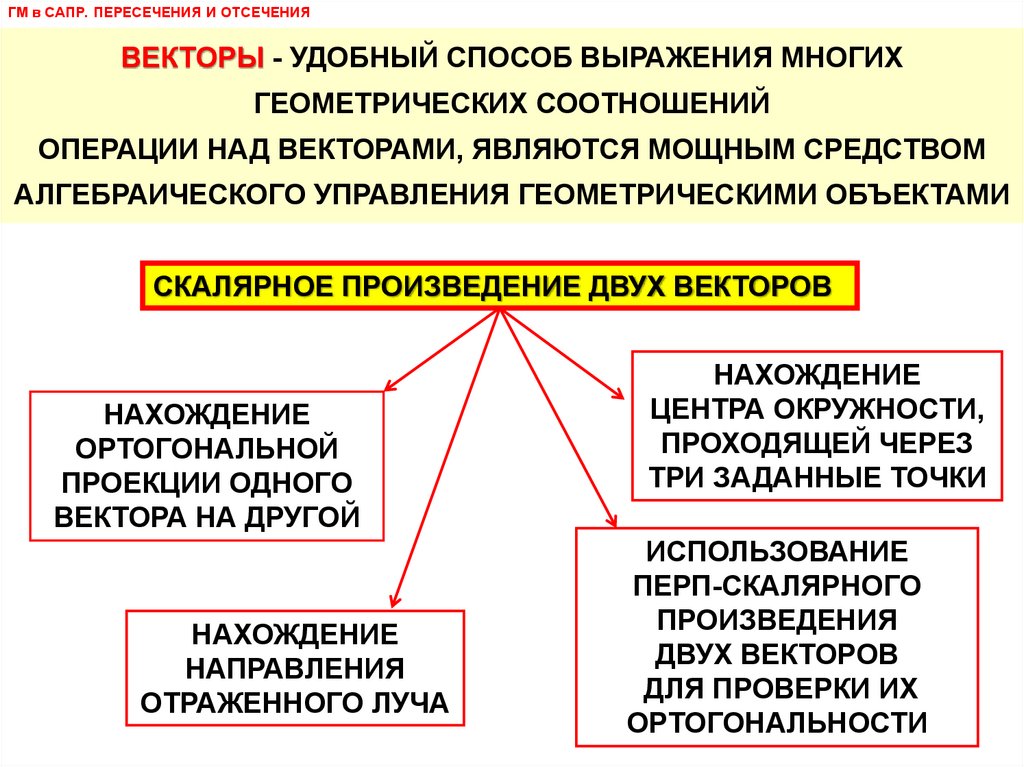
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВЕКТОРЫ - УДОБНЫЙ СПОСОБ ВЫРАЖЕНИЯ МНОГИХ
ГЕОМЕТРИЧЕСКИХ СООТНОШЕНИЙ
ОПЕРАЦИИ НАД ВЕКТОРАМИ, ЯВЛЯЮТСЯ МОЩНЫМ СРЕДСТВОМ
АЛГЕБРАИЧЕСКОГО УПРАВЛЕНИЯ ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
НАХОЖДЕНИЕ
ОРТОГОНАЛЬНОЙ
ПРОЕКЦИИ ОДНОГО
ВЕКТОРА НА ДРУГОЙ
НАХОЖДЕНИЕ
НАПРАВЛЕНИЯ
ОТРАЖЕННОГО ЛУЧА
НАХОЖДЕНИЕ
ЦЕНТРА ОКРУЖНОСТИ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ
ТРИ ЗАДАННЫЕ ТОЧКИ
ИСПОЛЬЗОВАНИЕ
ПЕРП-СКАЛЯРНОГО
ПРОИЗВЕДЕНИЯ
ДВУХ ВЕКТОРОВ
ДЛЯ ПРОВЕРКИ ИХ
ОРТОГОНАЛЬНОСТИ
29.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ ИСПОЛЬЗУЮТ
ДЛЯ ОПРЕДЕЛЕНИЯ ВЕКТОРА НОРМАЛИ К ПЛОСКОСТИ
ОЧЕНЬ ПОЛЕЗНЫМИ В ГРАФИКЕ ЯВЛЯЮТСЯ
АФФИННЫЕ КОМБИНАЦИИ ТОЧЕК
КОТОРЫЕ СОСТАВЛЯЮТ ОСНОВУ «ТВИНИНГА»
(ПОСТРОЕНИЯ ПРОМЕЖУТОЧНЫХ ОТОБРАЖЕНИЙ) ДЛЯ АНИМАЦИИ
ПРИ РАЗРАБОТКЕ АЛГОРИТМОВ ВАЖНО ИМЕТЬ КОМПАКТНОЕ
ПРЕДСТАВЛЕНИЕ УЧАСТВУЮЩИХ В НИХ ФУНДАМЕНТАЛЬНЫХ
ОБЪЕКТОВ ГРАФИКИ: ПРЯМЫХ И ПЛОСКОСТЕЙ
В ПАРАМЕТРИЧЕСКОЙ И ТОЧЕЧНО-НОРМАЛЬНОЙ ФОРМЕ
ПАРАМЕТРИЧЕСКАЯ ФОРМА ПРЯМОЙ ЛИНИИ
ОСОБЕННО УДОБНА В ТАКИХ ЗАДАЧАХ, КАК
ОПРЕДЕЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ПРЯМЫХ
ИЛИ НАХОЖДЕНИЯ
ТОЧЕК ПЕРЕСЕЧЕНИЯ ЛУЧА С МНОГОУГОЛЬНИКОМ
30.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ31.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИМЕР 8
НАЙТИ ПАРАМЕТРИЧЕСКУЮ ФОРМУ СРЕДИННОГО
ПЕРПЕНДИКУЛЯРА L(t) ДЛЯ ОТРЕЗКА S, ИМЕЮЩЕГО
КОНЦЕВЫЕ ТОЧКИ:
A = (3, 5) И В = (9, 3)
32.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИМЕР 8
НАЙТИ ПАРАМЕТРИЧЕСКУЮ ФОРМУ СРЕДИННОГО
ПЕРПЕНДИКУЛЯРА L(t) ДЛЯ ОТРЕЗКА S, ИМЕЮЩЕГО
КОНЦЕВЫЕ ТОЧКИ:
A = (3, 5) И В = (9, 3)
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР —
ЭТО МНОЖЕСТВО ВСЕХ ТОЧЕК,
РАВНОУДАЛЕННЫХ ОТ ДВУХ
ЗАДАННЫХ ТОЧЕК
A B
L(t ) M n t
( B A) t
2
(12, 8)
L(t )
(6, 2) t 6, 4 2, 6 t
2
6 2 t , 4 6 t
33.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПРИМЕР 9
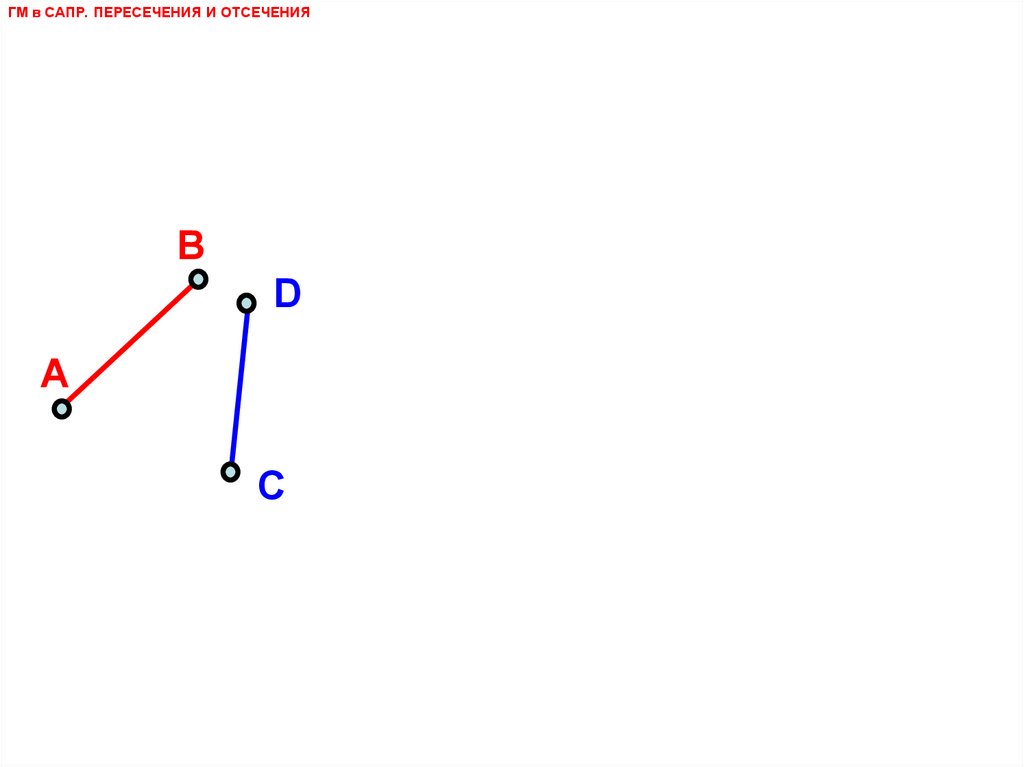
ОПРЕДЕЛИТЬ ТОЧКУ ПЕРЕСЕЧЕНИЯ ОТРЕЗКОВ
AB И CD, ЕСЛИ ИЗВЕСТНЫ КООРДИНАТЫ
ИХ КОНЦЕВЫХ ТОЧЕК:
а) A = (-1, -1), В = (2, 1), C=(0, 2), D=(2, 0)
б) A = (-1, -1), В = (2, 1), C=(-2,-2), D=(4, 2)
34.
ПРИМЕР 9ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯ
ОПРЕДЕЛИТЬ ТОЧКУ ПЕРЕСЕЧЕНИЯ ОТРЕЗКОВ AB И CD,
ЕСЛИ ИЗВЕСТНЫ КООРДИНАТЫ ИХ КОНЦЕВЫХ ТОЧЕК:
d D C (2, 2)
b B A 3, 2
c C A (1, 3)
а) A = (-1, -1), В = (2, 1), C=(0, 2), D=(2, 0)
d c
t
d b
b c
u
d b
d b d x by d y bx 10
t 0,8 ; u 0,7
AB(t ) A b t
d D C (6, 4)
b B A 3, 2
c C A ( 1, 1)
t, u
0, 1
x 1,4; y 0,6
б) A = (-1, -1), В = (2, 1), C=(-2,-2), D=(4, 2)
d b d x by d y bx 0
35.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯB
D
A
C
36.
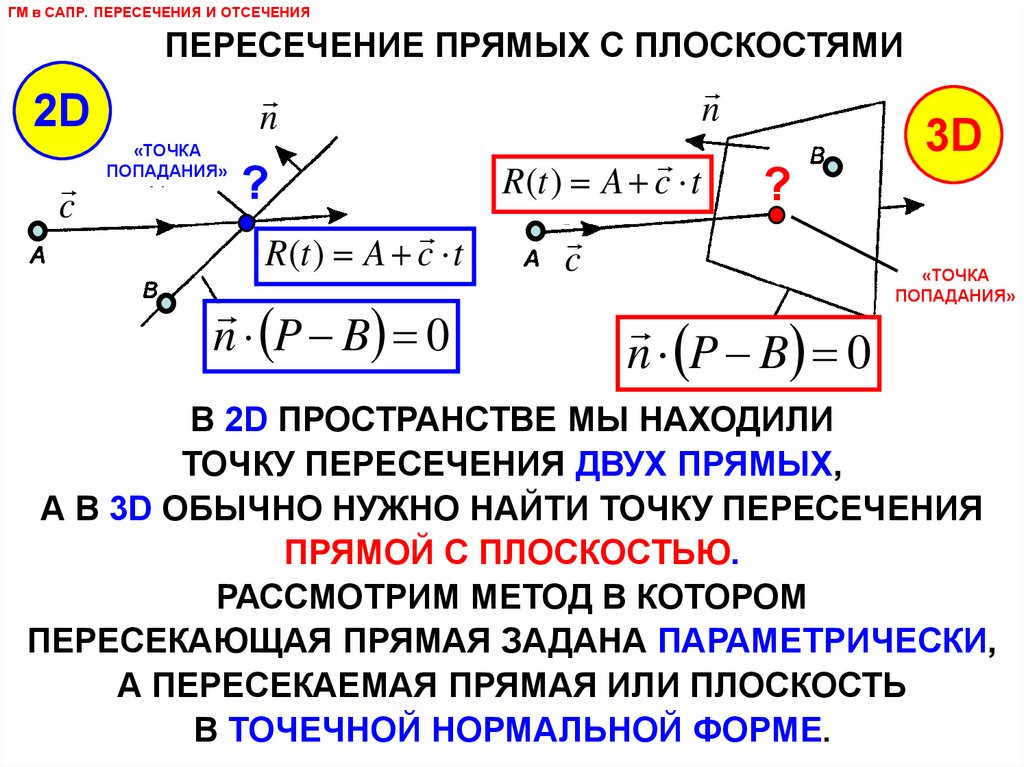
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯПЕРЕСЕЧЕНИЕ ПРЯМЫХ С ПЛОСКОСТЯМИ
2D
c
n
n
«ТОЧКА
ПОПАДАНИЯ»
?
R (t ) A c t
n P B 0
R (t ) A c t
c
3D
?
n P B 0
«ТОЧКА
ПОПАДАНИЯ»
В 2D ПРОСТРАНСТВЕ МЫ НАХОДИЛИ
ТОЧКУ ПЕРЕСЕЧЕНИЯ ДВУХ ПРЯМЫХ,
А В 3D ОБЫЧНО НУЖНО НАЙТИ ТОЧКУ ПЕРЕСЕЧЕНИЯ
ПРЯМОЙ С ПЛОСКОСТЬЮ.
РАССМОТРИМ МЕТОД В КОТОРОМ
ПЕРЕСЕКАЮЩАЯ ПРЯМАЯ ЗАДАНА ПАРАМЕТРИЧЕСКИ,
А ПЕРЕСЕКАЕМАЯ ПРЯМАЯ ИЛИ ПЛОСКОСТЬ
В ТОЧЕЧНОЙ НОРМАЛЬНОЙ ФОРМЕ.
37.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯt ВХ max (0 , t ВХ ) t ВЫХ min (t ВЫХ , 1)
ВОЗМОЖНЫЙ ИНТЕРВАЛ
t 0, 1
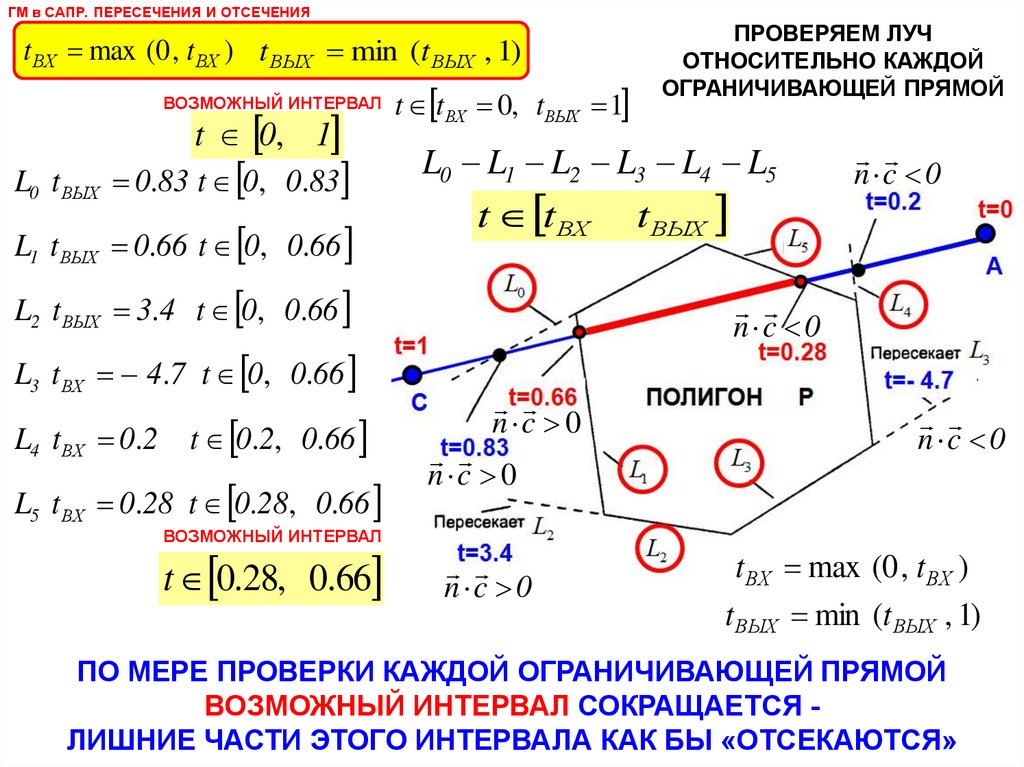
L0 t ВЫХ 0.83 t 0, 0.83
L1 t ВЫХ 0.66 t 0, 0.66
t tВХ 0, tВЫХ 1
L0 L1 L2 L3 L4 L5
t t ВХ t ВЫХ
L2 t ВЫХ 3.4 t 0, 0.66
L3 t ВХ 4.7 t 0, 0.66
L4 t ВХ 0.2
t 0.2, 0.66
L5 t ВХ 0.28 t 0.28, 0.66
n c 0
n c 0
n c 0
n c 0
ВОЗМОЖНЫЙ ИНТЕРВАЛ
t 0.28, 0.66
ПРОВЕРЯЕМ ЛУЧ
ОТНОСИТЕЛЬНО КАЖДОЙ
ОГРАНИЧИВАЮЩЕЙ ПРЯМОЙ
n c 0
n c 0
t ВХ max (0 , t ВХ )
t ВЫХ min (t ВЫХ , 1)
ПО МЕРЕ ПРОВЕРКИ КАЖДОЙ ОГРАНИЧИВАЮЩЕЙ ПРЯМОЙ
ВОЗМОЖНЫЙ ИНТЕРВАЛ СОКРАЩАЕТСЯ ЛИШНИЕ ЧАСТИ ЭТОГО ИНТЕРВАЛА КАК БЫ «ОТСЕКАЮТСЯ»
38.
t=0.2L5
L0
А
L4
t=1
С
L3
t=0.28
t=0.66
t=0.83
t=3.4
t=0
ПОЛИГОН
L1
L2
P
t=- 4.7
L3
L2
ПО МЕРЕ ПРОВЕРКИ КАЖДОЙ ОГРАНИЧИВАЮЩЕЙ ПРЯМОЙ
ВОЗМОЖНЫЙ ИНТЕРВАЛ СОКРАЩАЕТСЯ- ЧАСТИ ЭТОГО ИНТЕРВАЛА
КАК БЫ «ОТСЕКАЮТСЯ»
АЛГОРИТМ САЙРУСА–БЕКА [CYRUS, BECK, 1978]
t 0.28, 0.66
39.
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯn
ОТСЕЧЕНИЕ ВЫПУКЛЫХ ПОЛИГОНОВ
t ВЫХ
B
n
ЗАДАЧА ОТСЕЧЕНИЯ
n (B A)
t
n c
B
t t ВХ
ВЫПУКЛЫЙ ПОЛИГОН P
n
C
t ВХ A ПОЛИГОН P
A
ЛУЧ L(t ) A c t ПЕРЕСЕКАЕТ
t ВЫХ
c C A C
L(t ) A c t
t ВХ
A
t 0
A
(а)
t ВЫХ
A
C
C
t ВХ
tВЫХ 1
tВЫХ 1
t 1
C
КАКАЯ ЧАСТЬ ОТРЕЗКА
ПРЯМОЙ АС ДЛЯ ЗАДАННЫХ
ТОЧЕК А И С НАХОДИТСЯ
ВНУТРИ ПОЛИГОНА Р ?
1
A (б)
t ВХ 0
A A c t ВХ t 0 A A c t ВХ
C tВЫХ 1
C A c t ВЫХ
1
A
0
(в)
A
C
t ВХ 0
tВЫХ 1
40.
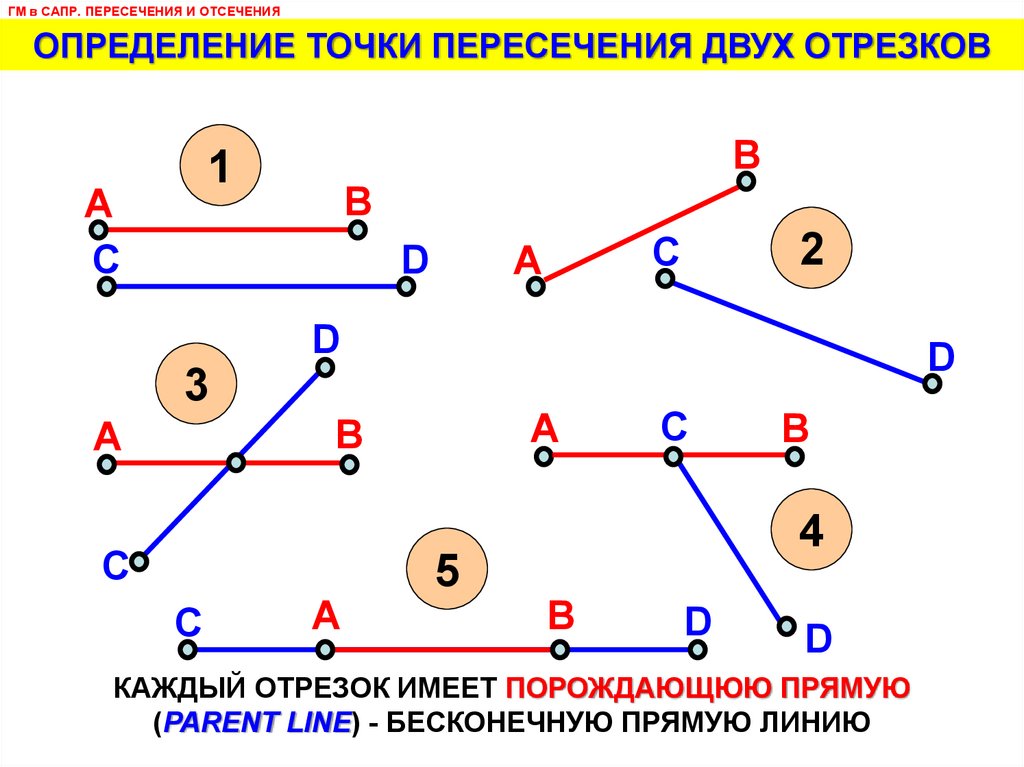
ГМ в САПР. ПЕРЕСЕЧЕНИЯ И ОТСЕЧЕНИЯОПРЕДЕЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ДВУХ ОТРЕЗКОВ
B
1
A
C
B
D
2
C
A
D
D
3
A
B
A
C
C
4
5
C
A
B
B
D
D
КАЖДЫЙ ОТРЕЗОК ИМЕЕТ ПОРОЖДАЮЩЮЮ ПРЯМУЮ
(PARENT LINE) - БЕСКОНЕЧНУЮ ПРЯМУЮ ЛИНИЮ


















 Математика
Математика