Признаки параллельности двух прямых. Параллельные отрезки. Прямоугольник

1. Признаки параллельности двух прямых.

2. Цель:

Актуализировать знания учащихся о
параллельных прямых, полученные в 5
классе;
Ввести определение параллельных
прямых, параллельных отрезков;
Познакомить с накрест лежащими,
односторонними, соответственными
углами, с признаками параллельности
двух прямых.

3. Две прямые на плоскости называются параллельными, если они не пересекаются

B
N
A
M
АВ MN

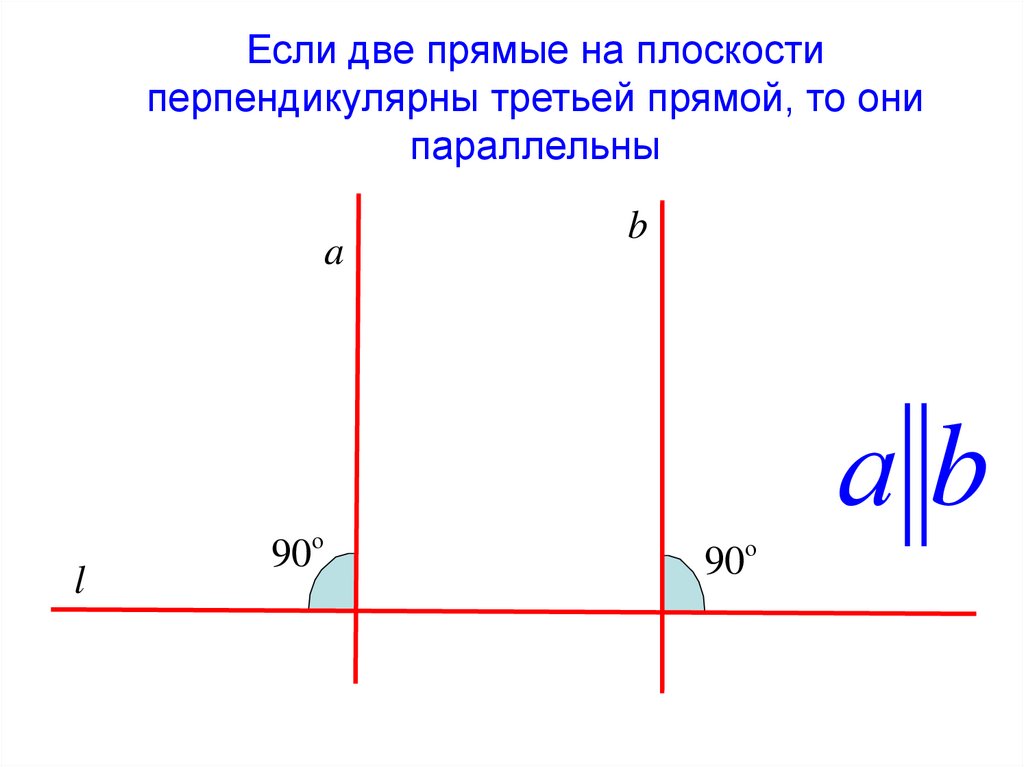
4. Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны

a
l
90о
b
аb
90о

5. Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной

p
l
А
b
а
b || а
р
a
l
a

6. Два отрезка называются параллельными, если они лежат на параллельных прямых

аb
B
A
D
а
С
b
АВ СД

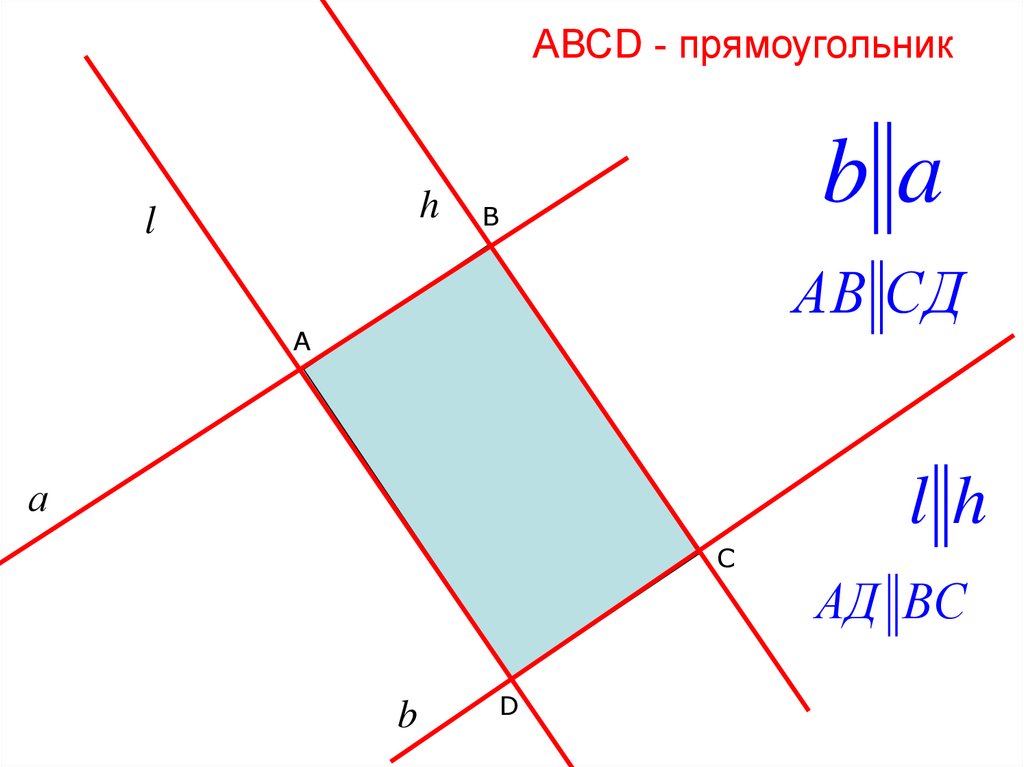
7. АВСD - прямоугольник

h
l
ba
B
АВ СД
A
а
lh
С
b
D
AД ВС

8. Определения

1
а
Прямая с называется секущей
по отношению к прямым
4
а и b, если она пересекает
их в двух точках
Названия углов
накрест лежащие углы:
b
3 и 5, 4 и 6
односторонние углы:
5
8
4 и 5, 3 и 6
соответственные углы:
1 и 5, 4 и 8, 2 и 6, 3 и 7
с
6
7
2
3

9. Теорема

Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны
а
Н
Дано: АВ пересекает прямые a и b.
А
1
Доказать:
1 2
О
аb
Доказательство
ОНА
ОН1В
Выполним
построения:
1. Отметим середину отрезка АВ. АО=ОВ
b
2
В
2. ОН а
Н1
ОНА ОН1В
3. На прямой b от точки В отложим
ВН1 АН и проведем отрезок
АО? ОВ, АН ВН1, 1 2
ОН1

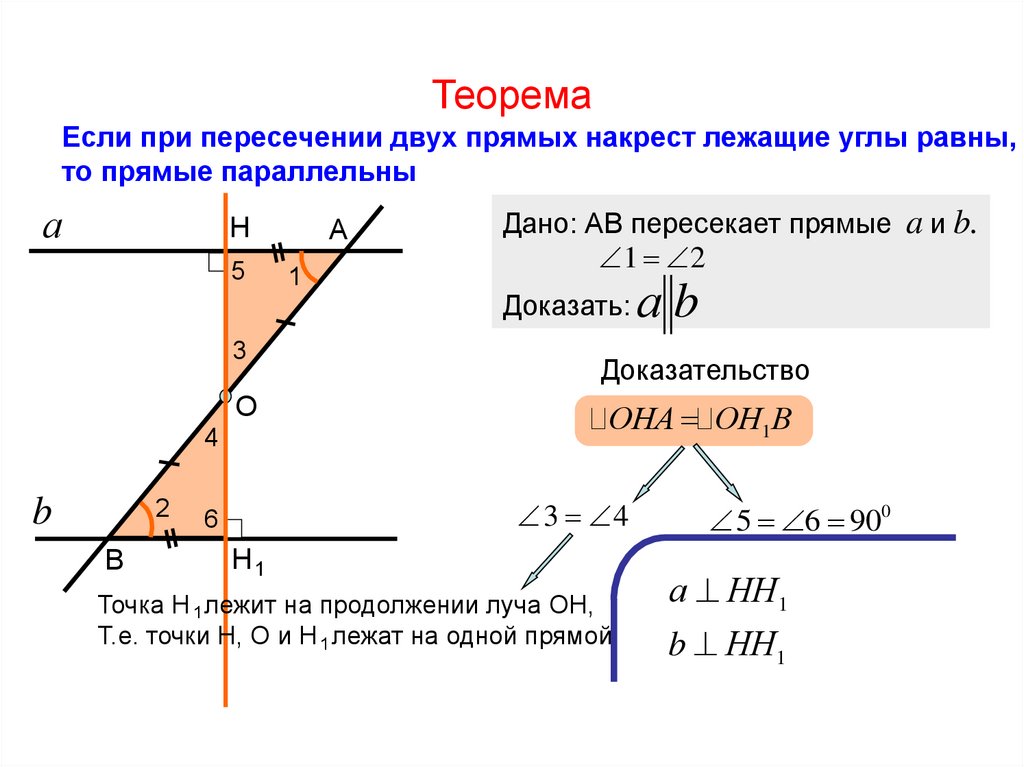
10. Теорема

Если при пересечении двух прямых накрест лежащие углы равны,
то прямые параллельны
а
Н
5
3
О
4
b
2
В
А
1
Дано: АВ пересекает прямые a и b.
1 2
Доказать:
Доказательство
ОНА ОН1В
3 4
6
аb
Н1
Точка Н 1 лежит на продолжении луча ОН,
Т.е. точки Н, О и Н 1 лежат на одной прямой
5 6 900
а НН1
а b
b НН1

11. Теорема

Если при пересечении двух прямых секущей соответственные
углы равны, то прямые параллельны
а
2
3
Дано: Секущая с пересекает
прямые a и b. 1 2
Доказать:
аb
Доказательство
1 2 по условию
?
2 3 вертикальные
?
b
1
с
1 3,
а они накрест лежащие
аb

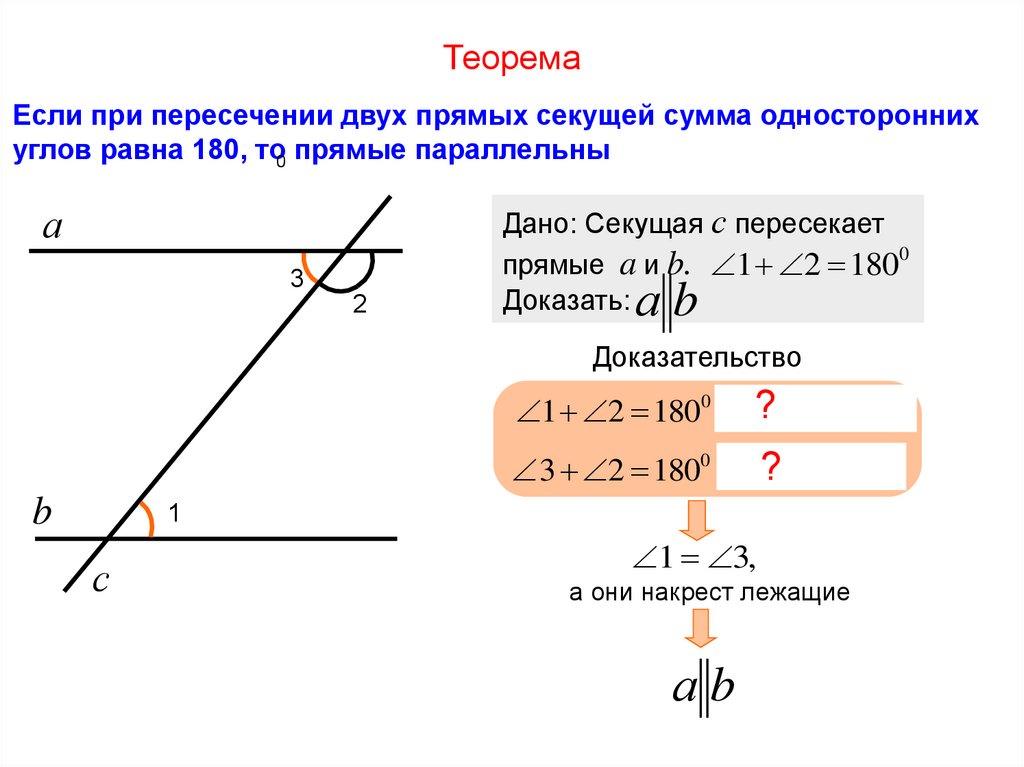
12. Теорема

Если при пересечении двух прямых секущей сумма односторонних
углов равна 180, то0 прямые параллельны
а
3
2
Дано: Секущая с пересекает
прямые a и b. 1 2 1800
Доказать:
аb
Доказательство
? условию
1 2 1800 по
?
3 2 1800 смежные
b
1
с
1 3,
а они накрест лежащие
аb

13.

1
3
2
4
5 6
а
b
7
8
c
Назовите
односторонние,
накрест лежащие,
соответственные углы.

14.

а
1
2
b
6
c
7
5
8
4
3

15.

1
а
2
b
c

16. Дома:

П 24-25