Похожие презентации:
Ассоциативные массивы (Алгоритмы и структуры данных)
1.
Перевод: английский - русский - www.onlinedoctranslator.comАссоциативные массивы
(Алгоритмы и структуры
данных)
2.
Ассоциативные массивы• ассоциативные массивы (карты или словари)абстрактные типы
данных
• состоит изколлекция пар ключ-значениегде каждый ключ
появляется в коллекции не более одного раза
• В большинстве случаев мы реализуем ассоциативные массивы с
помощью хеш-таблиц, но можно использовать и двоичные
деревья поиска.
• цель состоит в том, чтобы достичьО(1)временная сложность
большинства операций
3.
Ассоциативные массивы• ассоциативные массивы (карты или словари)абстрактные типы
данных
• состоит изколлекция пар ключ-значениегде каждый ключ
появляется в коллекции не более одного раза
ПОЛЬЗОВАТЕЛЬ ЭЛЕКТРОННОЙ ПОЧТЫ
к.смит@gmai.com
a.jobs@yahoo.com
daniel@gmail.com
Пользователь(‚Кевин Смит', 34)
Пользователь(‚Ана Джобс', 26)
Пользователь(‚Дэниел Маск', 48)
4.
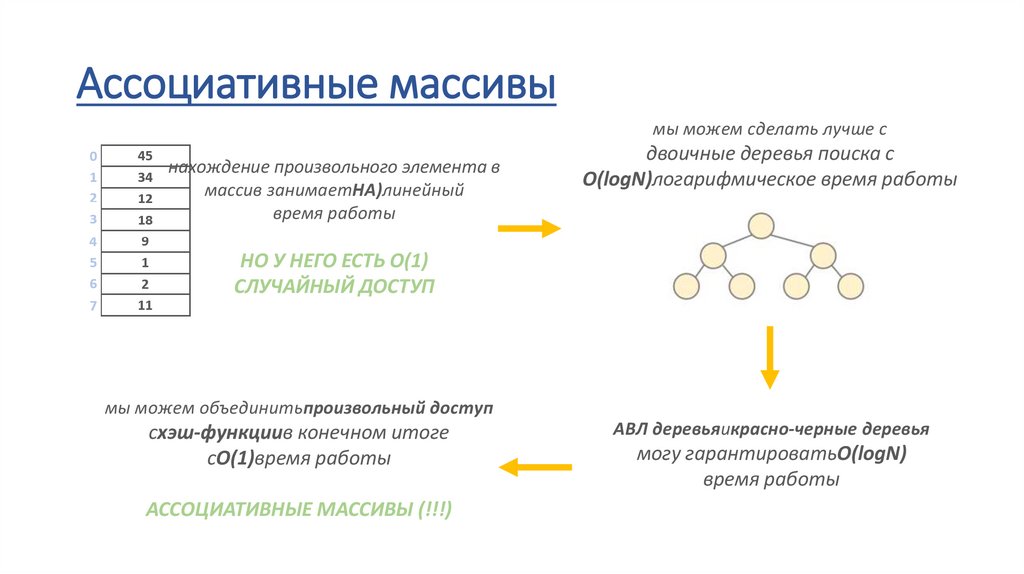
Ассоциативные массивымы можем сделать лучше с
нахождение произвольного элемента в
массив занимаетНА)линейный
время работы
двоичные деревья поиска с
О(logN)логарифмическое время работы
НО У НЕГО ЕСТЬ O(1)
СЛУЧАЙНЫЙ ДОСТУП
мы можем объединитьпроизвольный доступ
схэш-функциив конечном итоге
сО(1)время работы
АССОЦИАТИВНЫЕ МАССИВЫ (!!!)
АВЛ деревьяикрасно-черные деревья
могу гарантироватьО(logN)
время работы
5.
Ассоциативные массивы• есть несколько операций, которые мы хотим реализовать, и мы
хотим, чтобы эти операции имелиО(1)время работы
• добавлениепары (ключ, значение) в коллекцию
• удалениепары (ключ, значение) в коллекцию
• искатьзаданное значение, связанное с заданным ключом
• Пары ключ-значение — вот почему ассоциативные массивы не
поддерживаютсортировкакак операция
6.
Хеш-таблицы(Алгоритмы и структуры
данных)
7.
Хеш-таблицыМотивация в том, что мы хотим хранить(ключ,
значение)эффективно сочетается – так
чтовставлятьиудалятьоперации занимаютО(1)время работы
8.
Хеш-таблицыМотивация в том, что мы хотим хранить(ключ,
значение)эффективно сочетается – так
чтовставлятьиудалятьоперации занимаютО(1)время работы
КЛЮЧЕВЫЕ ЦЕННОСТИ
Гете Фауст
Шиллер Дон Карлос
Хайдеггер Бытие и время
мы хотели бы сохранитьавторыи
the названияих романов
и делать операции
вО(1)сложность времени выполнения
9.
Хеш-таблицыМотивация в том, что мы хотим хранить(ключ,
значение)эффективно сочетается – так
чтовставлятьиудалятьоперации занимаютО(1)время работы
КЛЮЧЕВЫЕ ЦЕННОСТИ
Пользователь daniel@gmail.com
(«Даниэль»,24)
kevin@gmail.com
Пользователь(„Кевин”,34)
adam@gmail.com
Пользователь(„Адам”,56)
мы хотели бы сохранитьавторыи
the названияих романов
и делать операции
вО(1)сложность времени выполнения
10.
Хеш-таблицыМотивация в том, что мы хотим хранить(ключ,
значение)эффективно сочетается – так
чтовставлятьиудалятьоперации занимаютО(1)время работы
КЛЮЧЕВЫЕ ЦЕННОСТИ
Пользователь daniel@gmail.com
(«Даниэль»,24)
kevin@gmail.com
Пользователь(„Кевин”,34)
adam@gmail.com
Пользователь(„Адам”,56)
мы хотели бы сохранитьавторыи
the названияих романов
и делать операции
вО(1)сложность времени выполнения
11.
Хеш-таблицы0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
12.
Хеш-таблицыВСТАВИТЬ(‚Кевин Смит', 34)
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
13.
Хеш-таблицыВСТАВИТЬ(‚Кевин Смит', 34)
0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
2
11
14.
Хеш-таблицыВСТАВИТЬ(‚Кевин Смит', 34)
0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
2
11
15.
Хеш-таблицы0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
2
11
16.
Хеш-таблицыВСТАВКА(‚Дэниел Маск', 19)
0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
2
11
17.
Хеш-таблицыВСТАВКА(‚Дэниел Маск', 19)
0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
Дэниел Маск - 19
11
18.
Хеш-таблицы0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
Дэниел Маск - 19
11
19.
Хеш-таблицы0
1
2
3
4
5
6
7
45
34
12
Кевин Смит - 34
9
1
Дэниел Маск - 19
11
• как достичьО(1)время выполнения
операций вставки и извлечения?
• мы должны преобразовать ключ в индекс
массива – чтобы достичьпроизвольный
доступ
• вот почемуключи должны быть
уникальнымичтобы избежать
использования тех же индексов
• ч(х)хэш-функция преобразует ключ в
индекс в диапазоне[0,м-1]
20.
Хеш-таблицы„Theч(х)хэш-функция сопоставляет ключи с индексами массива в
массиве
чтобы иметь возможность использоватьслучайная
индексацияи достичьО(1)время работы”
21.
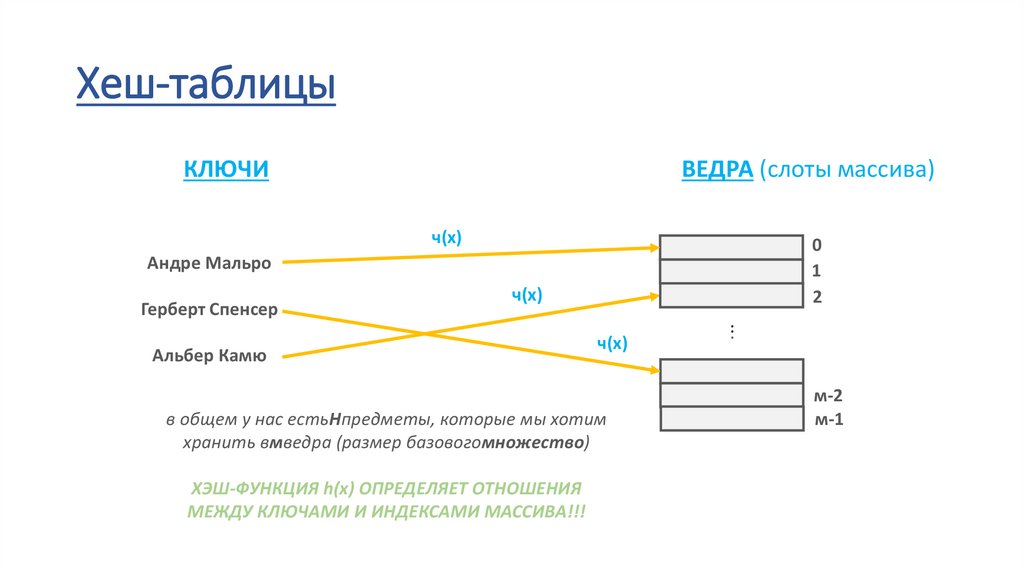
Хеш-таблицыКЛЮЧИ
ВЕДРА (слоты массива)
ч(х)
0
1
2
Андре Мальро
Герберт Спенсер
ч(х)
Альбер Камю
ч(х)
в общем у нас естьНпредметы, которые мы хотим
хранить вмведра (размер базовогомножество)
ХЭШ-ФУНКЦИЯ h(x) ОПРЕДЕЛЯЕТ ОТНОШЕНИЯ
МЕЖДУ КЛЮЧАМИ И ИНДЕКСАМИ МАССИВА!!!
..
.
м-2
м-1
22.
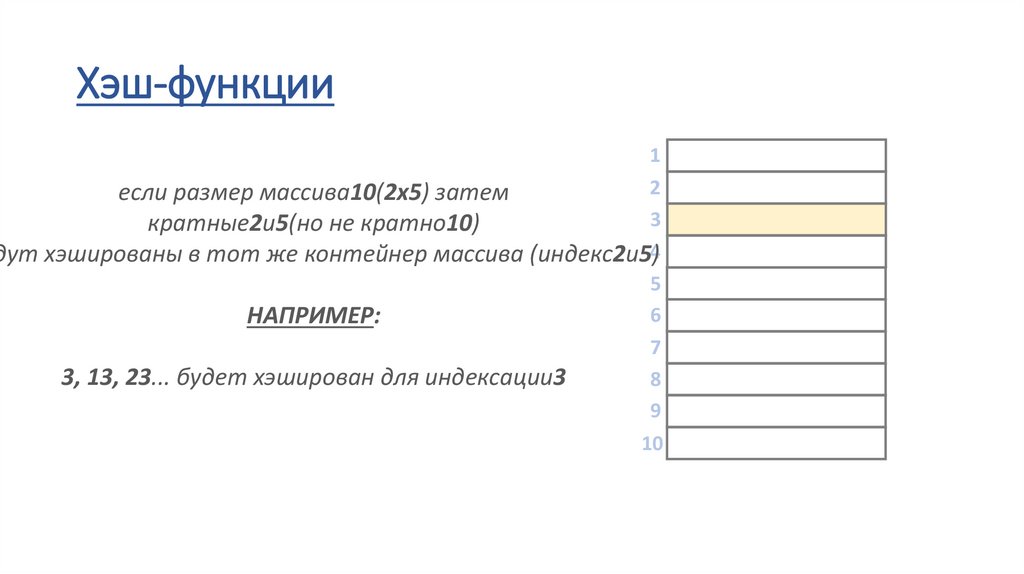
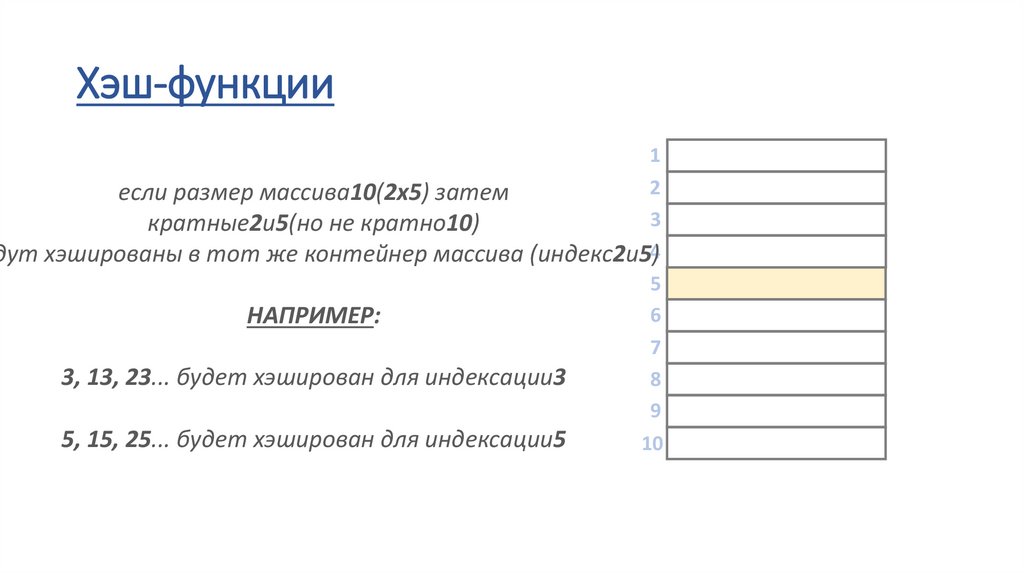
Хэш-функции• the ч(х)хэш-функция преобразует ключи в индексы массива
• он должен справитьсялюбые типы– строки, числа с плавающей
точкой, целые числа или даже пользовательские объекты
• если у нас естьцелочисленные ключинам просто нужно
использовать оператор по модулю (%), чтобы преобразовать
число в диапазон[0,м-1]
• мы можем использоватьASCIIзначения букв при работе со
строками
ХЭШ-ФУНКЦИЯ h(x) РАСПРЕДЕЛЯЕТ КЛЮЧИ
РАВНОМЕРНО В ВЕДРА (СЛОТЫ МАССИВА)!!!
23.
Хэш-функции0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
24.
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
25.
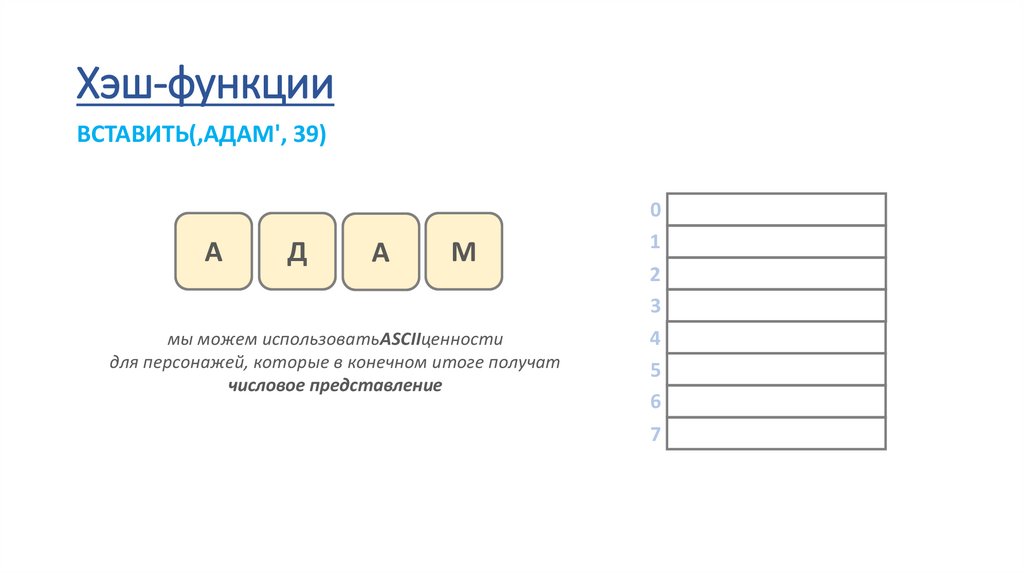
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
А
Д
А
М
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
26.
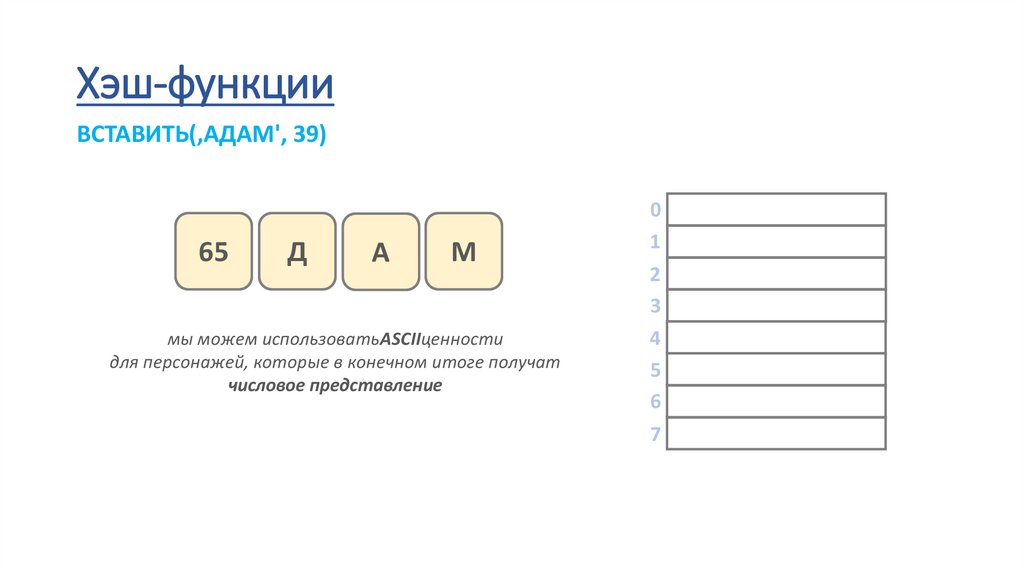
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
65
Д
А
М
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
27.
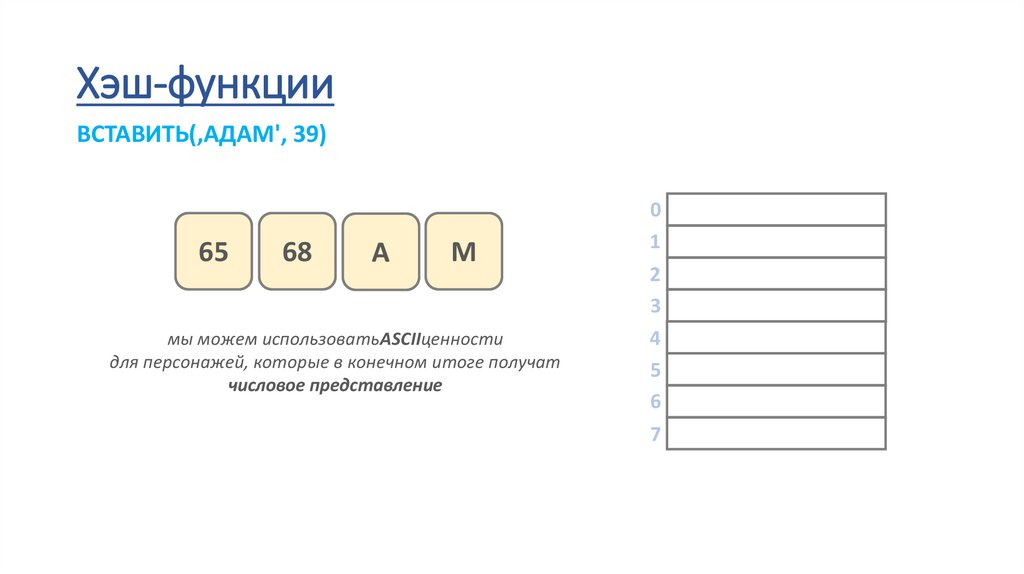
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
65
68
А
М
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
28.
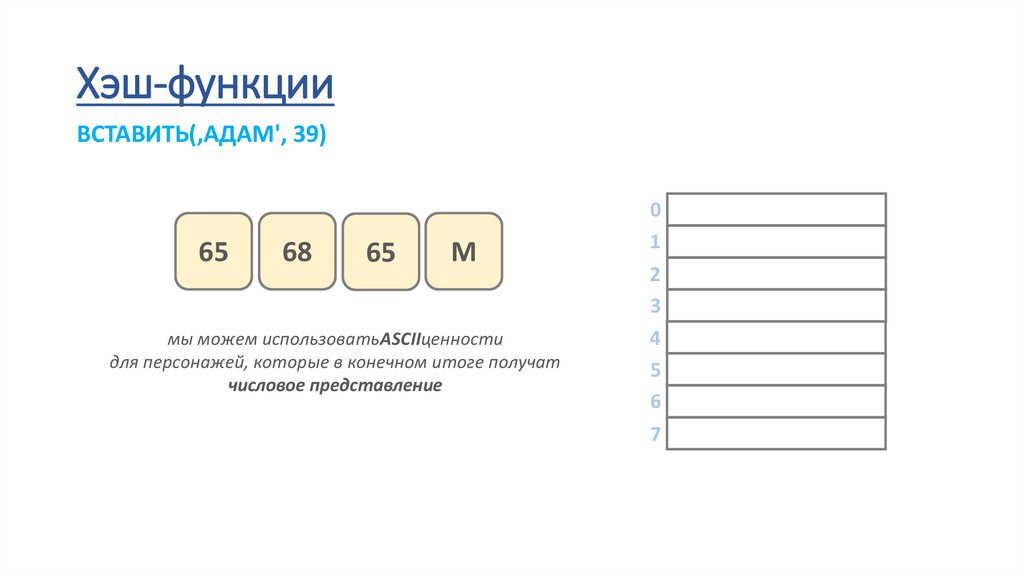
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
65
68
65
М
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
29.
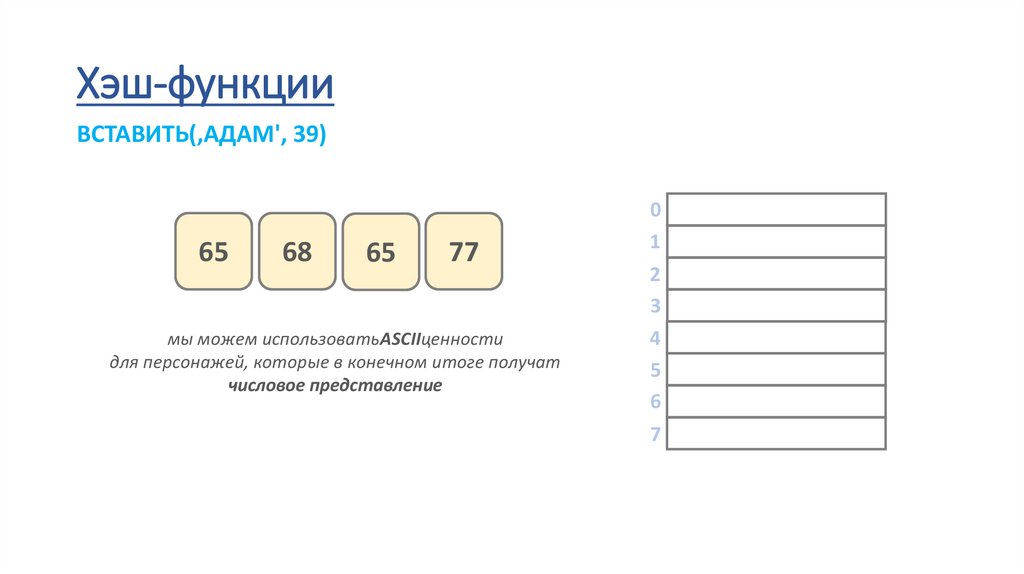
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
65
68
65
77
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
30.
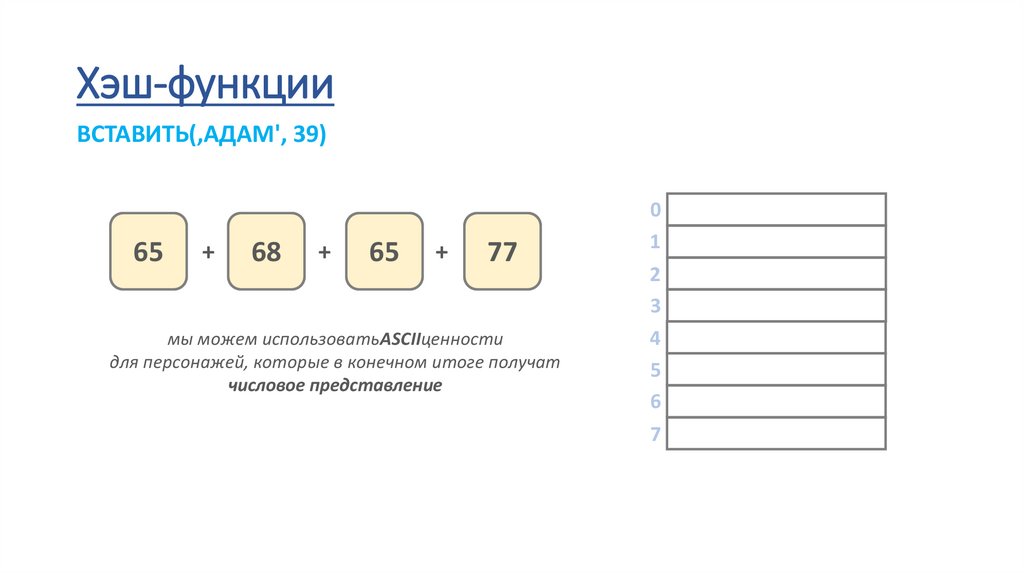
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
65
+
68
+
65
+
77
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
18
9
1
2
11
31.
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
275
0
1
2
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
4
5
6
+
7
мы должны убедиться, чтоиндексявляется
в диапазоне[0,м-1]
45
34
12
18
9
1
2
11
32.
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
275
%8
0
1
2
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
4
5
6
+
7
мы должны убедиться, чтоиндексявляется
в диапазоне[0,м-1]
45
34
12
18
9
1
2
11
33.
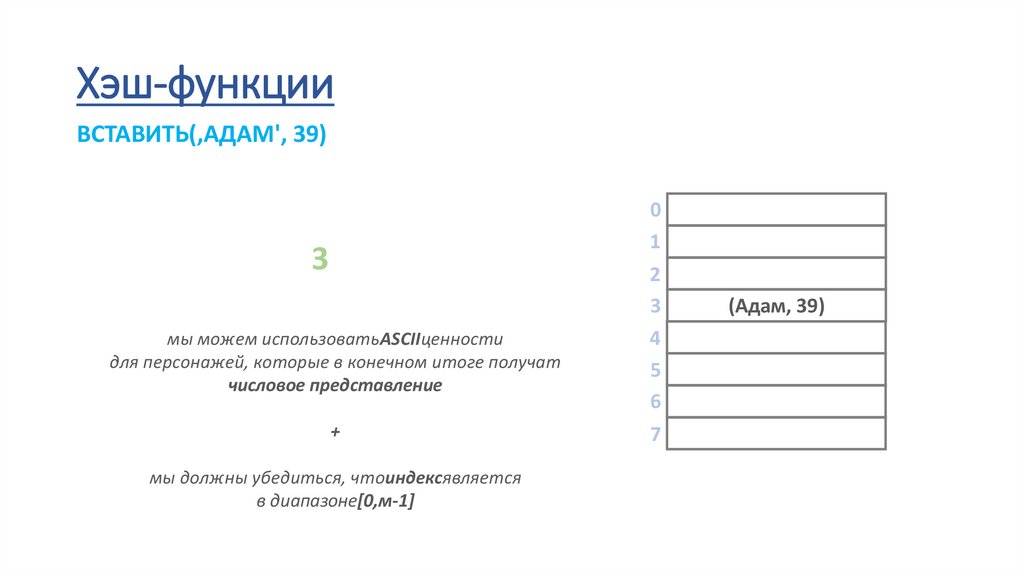
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
0
1
3
2
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
4
5
6
+
7
мы должны убедиться, чтоиндексявляется
в диапазоне[0,м-1]
45
34
12
18
9
1
2
11
34.
Хэш-функцииВСТАВИТЬ(‚АДАМ', 39)
0
1
3
2
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
4
5
6
+
7
мы должны убедиться, чтоиндексявляется
в диапазоне[0,м-1]
45
34
12
(Адам, 39)
9
1
2
11
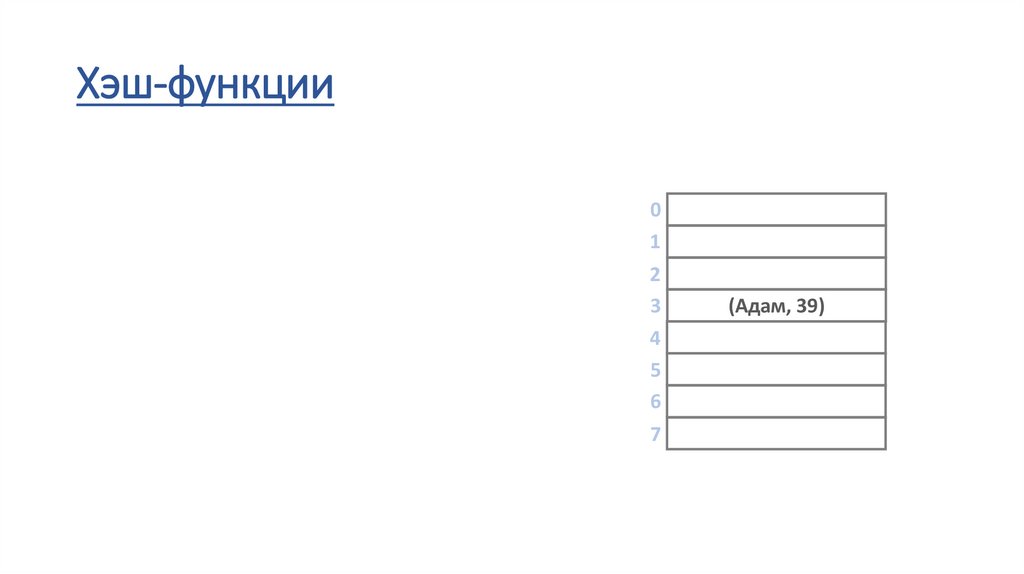
35.
Хэш-функции0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
36.
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
37.
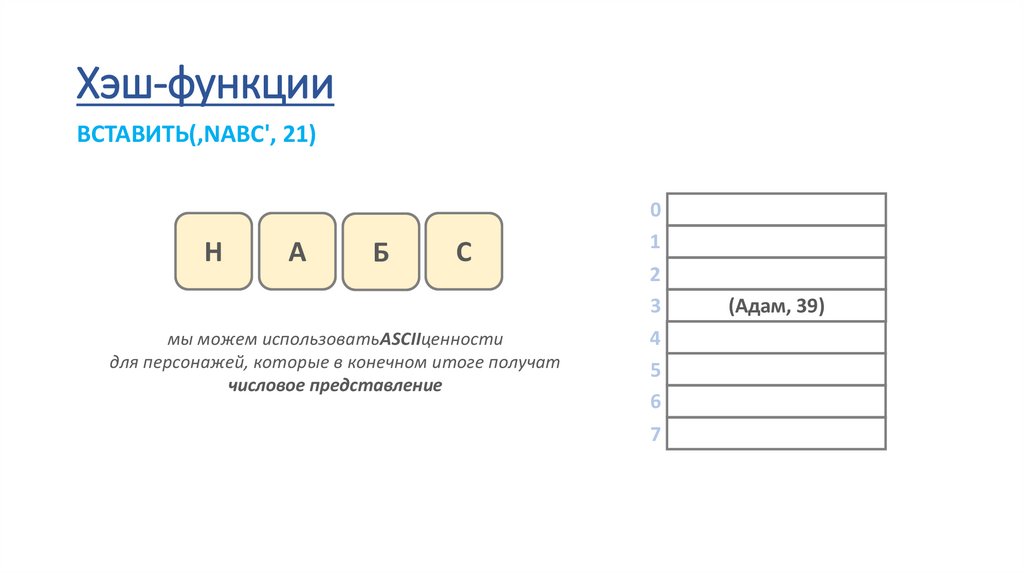
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
Н
А
Б
С
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
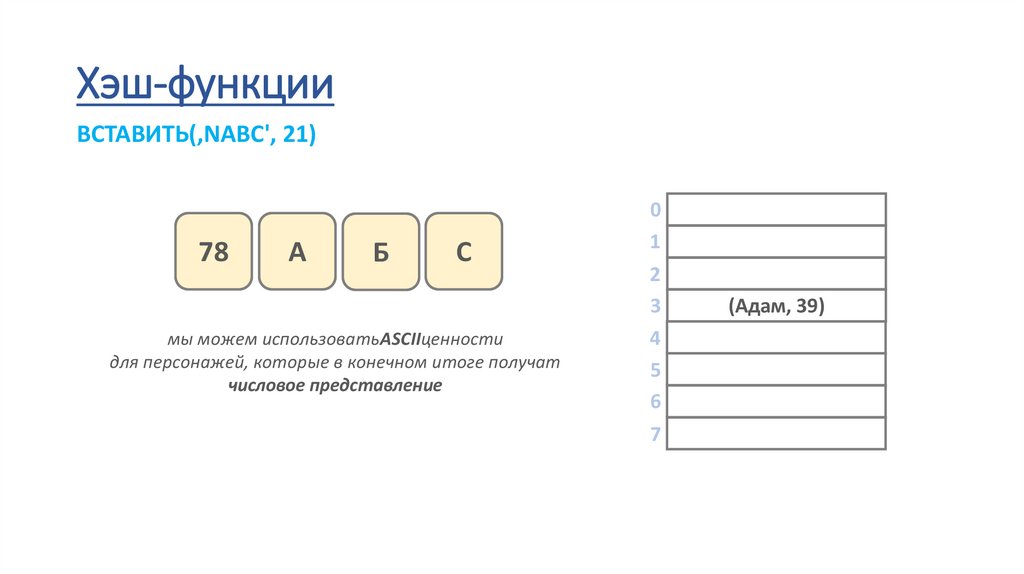
38.
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
78
А
Б
С
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
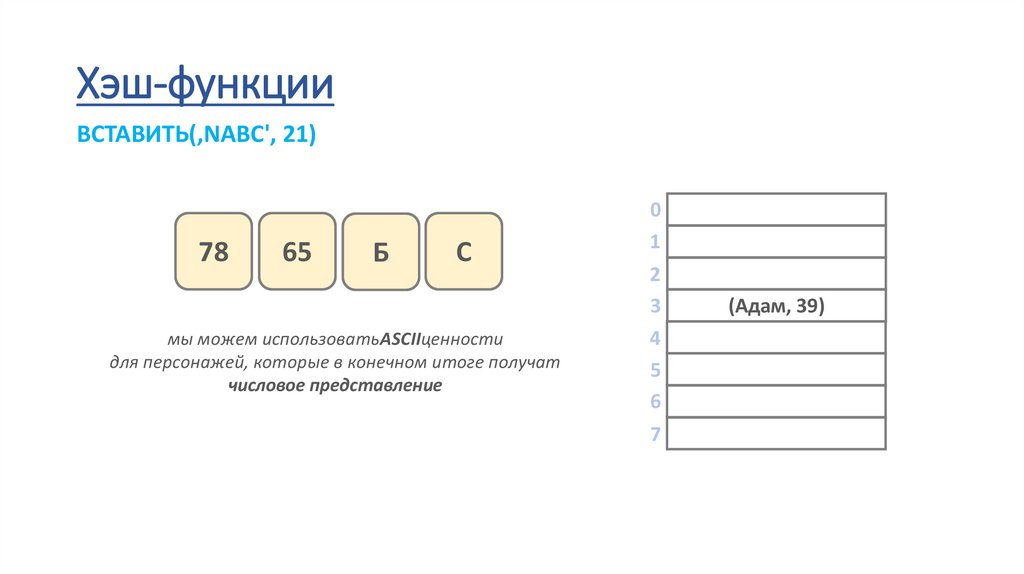
39.
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
78
65
Б
С
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
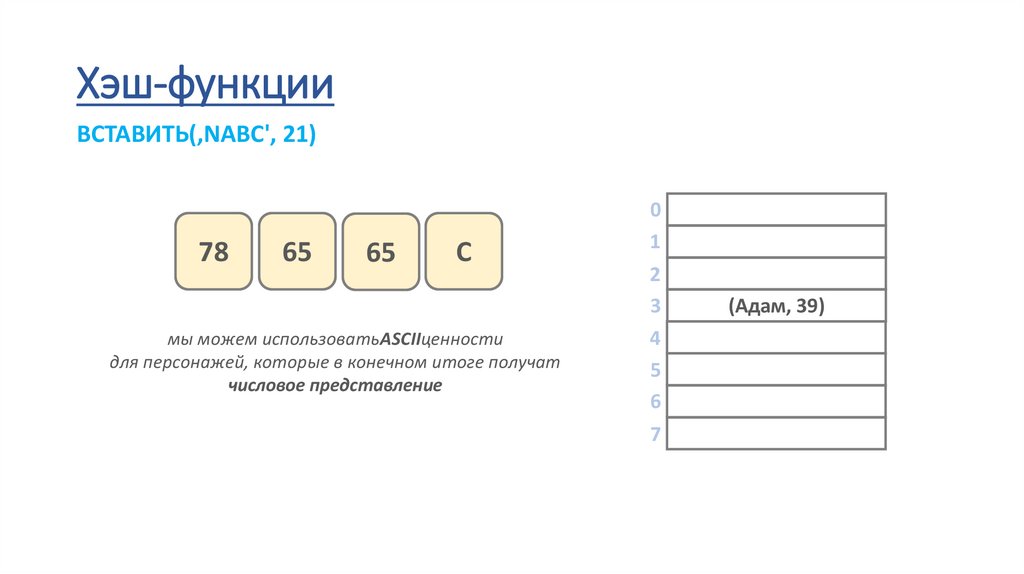
40.
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
78
65
65
С
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
41.
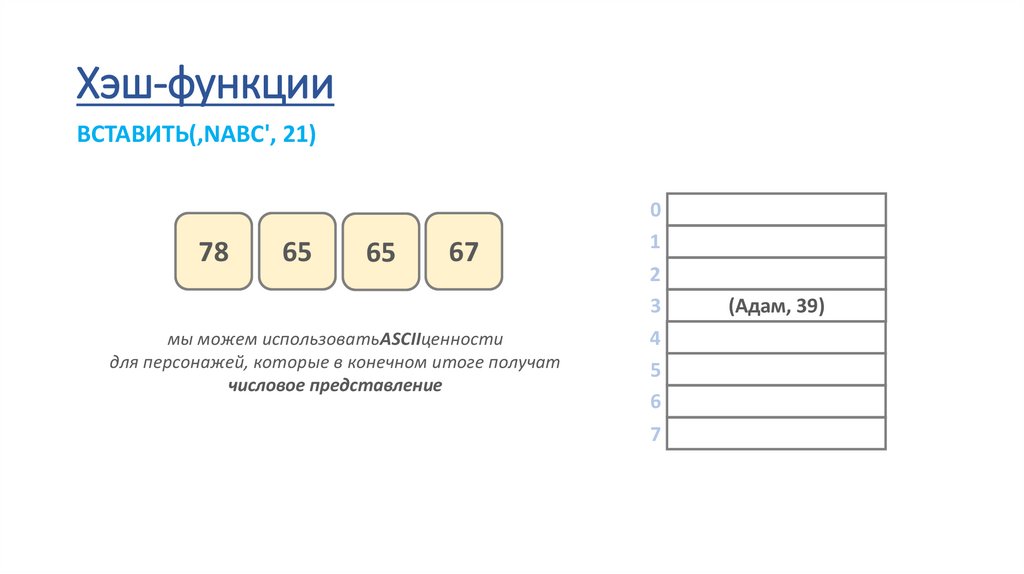
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
78
65
65
67
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
42.
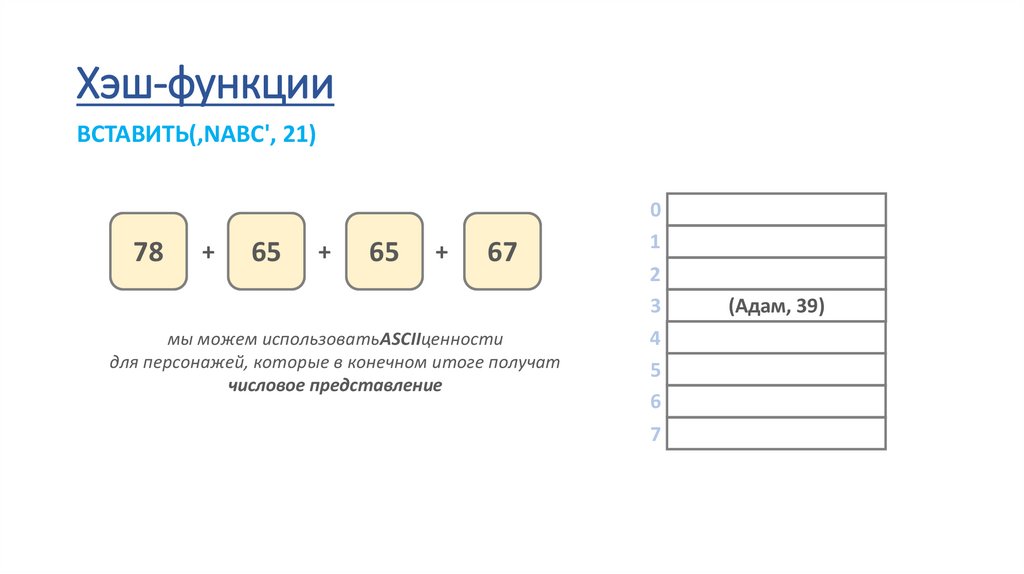
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
78
+
65
+
65
+
67
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
43.
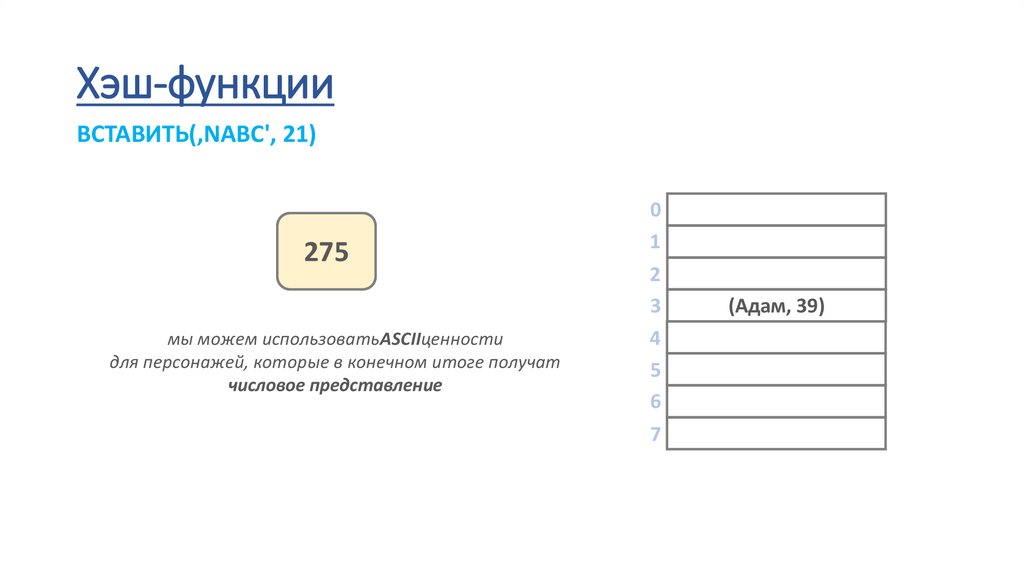
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
275
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
44.
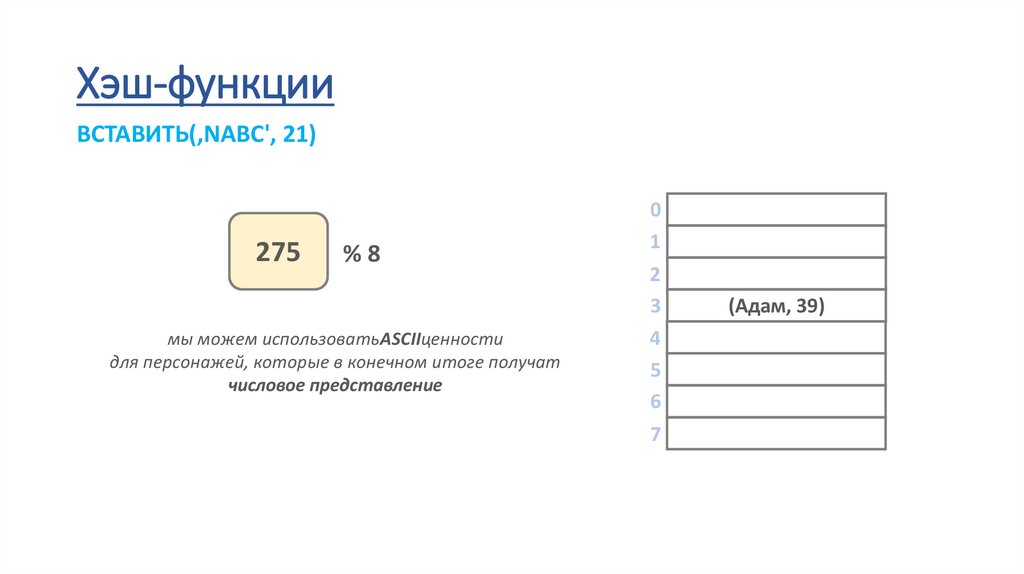
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
275
%8
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
45.
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
46.
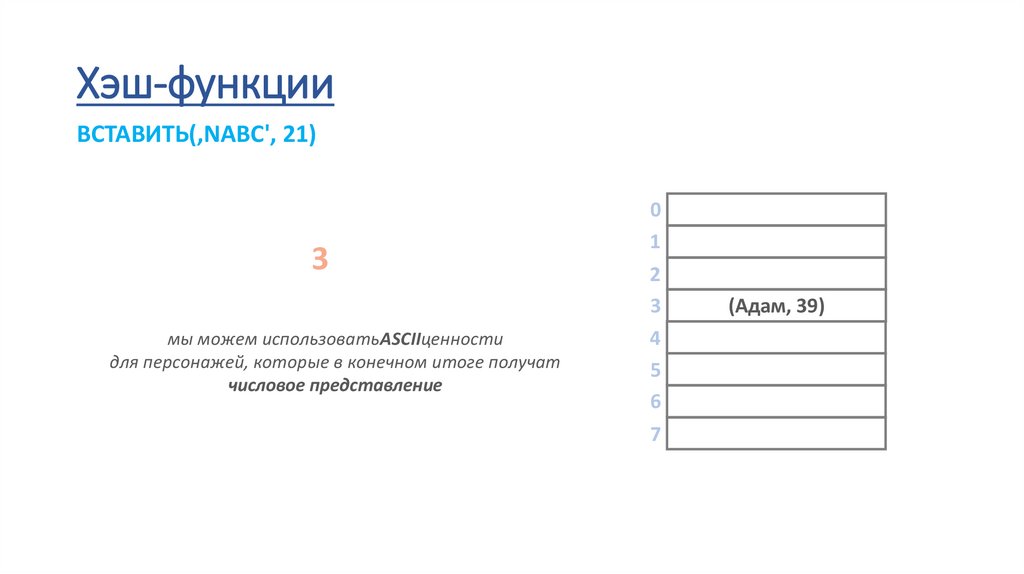
Хэш-функцииВСТАВИТЬ(‚NABC', 21)
3
мы можем использоватьASCIIценности
для персонажей, которые в конечном итоге получат
числовое представление
0
1
2
3
4
5
6
7
45
34
12
(Адам, 39)
9
1
2
11
47.
Столкновения(Алгоритмы и структуры
данных)
48.
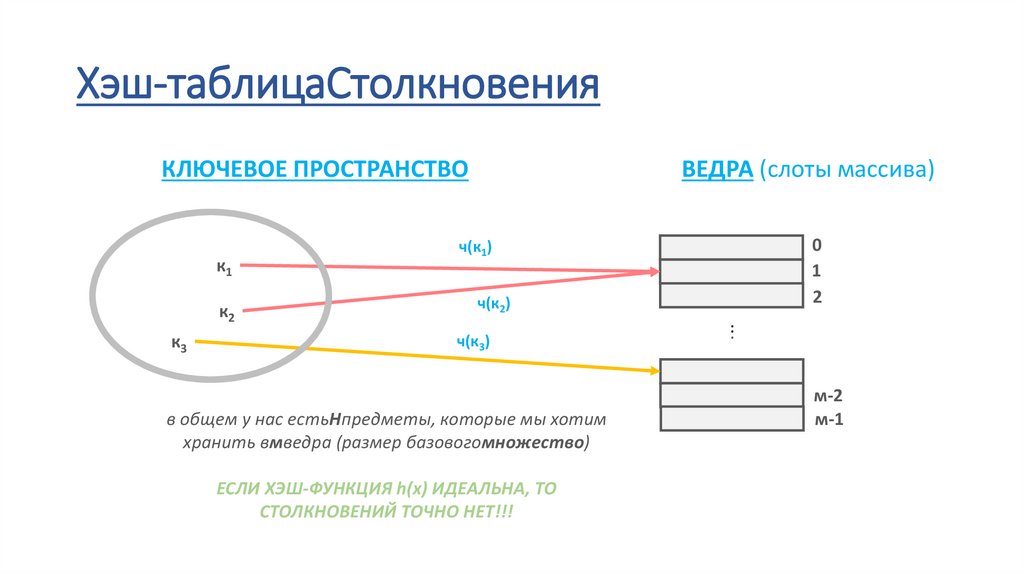
Хэш-таблицаСтолкновения„Столкновенияпроисходят, когдачас(х)карты хэш-функций
два ключа к одному и тому же слоту массива (ведру)”
49.
Хэш-таблицаСтолкновенияКЛЮЧЕВОЕ ПРОСТРАНСТВО
к1
к2
к3
ВЕДРА (слоты массива)
0
1
2
ч(к1)
ч(к2)
ч(к3)
в общем у нас естьНпредметы, которые мы хотим
хранить вмведра (размер базовогомножество)
ЕСЛИ ХЭШ-ФУНКЦИЯ h(x) ИДЕАЛЬНА, ТО
СТОЛКНОВЕНИЙ ТОЧНО НЕТ!!!
..
.
м-2
м-1
50.
Хэш-таблицаСтолкновения• the ч(х)хэш-функция определяет взаимосвязи между ключами и
индексами массива (корзинами)
• если хеш-функция идеальна, то естьнет столкновений
• в реальном миребудут столкновенияпотому что идеальных хешфункций не существует
51.
Хэш-таблицаСтолкновенияСуществует несколько подходов к решению проблемы столкновений:
1.) ЦЕПОЧКА
2.) ОТКРЫТОЕ ОБРАЩЕНИЕ
52.
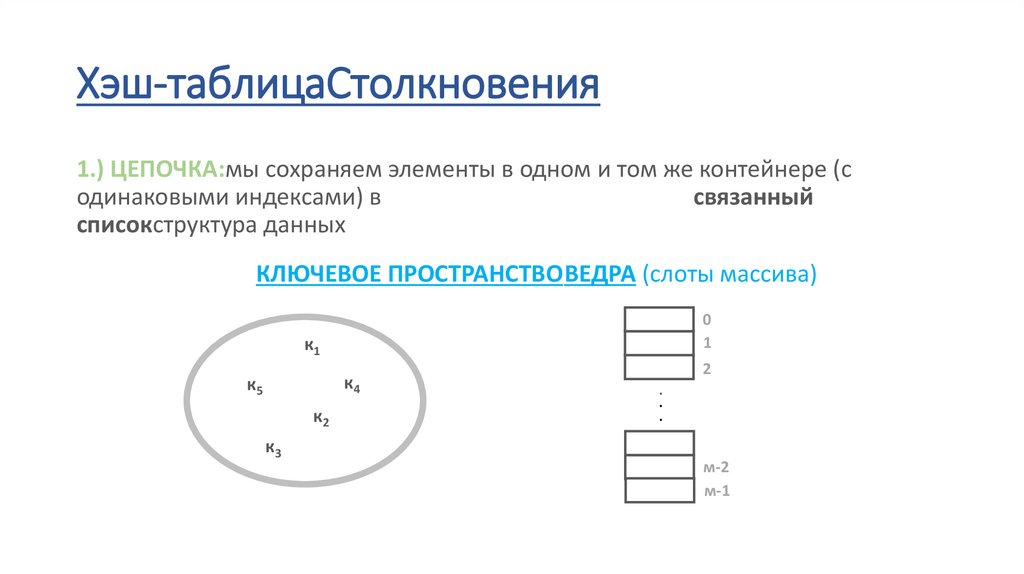
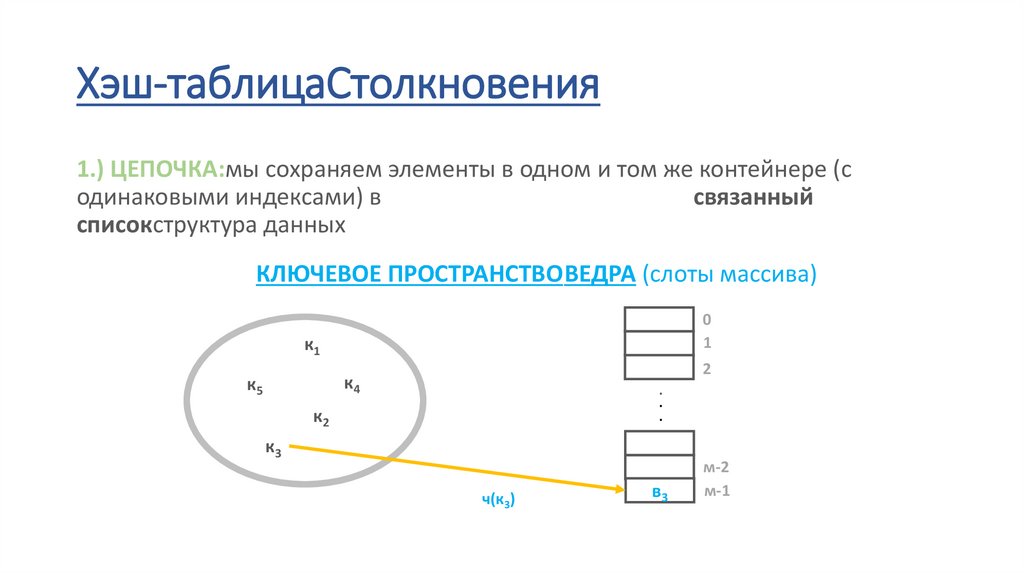
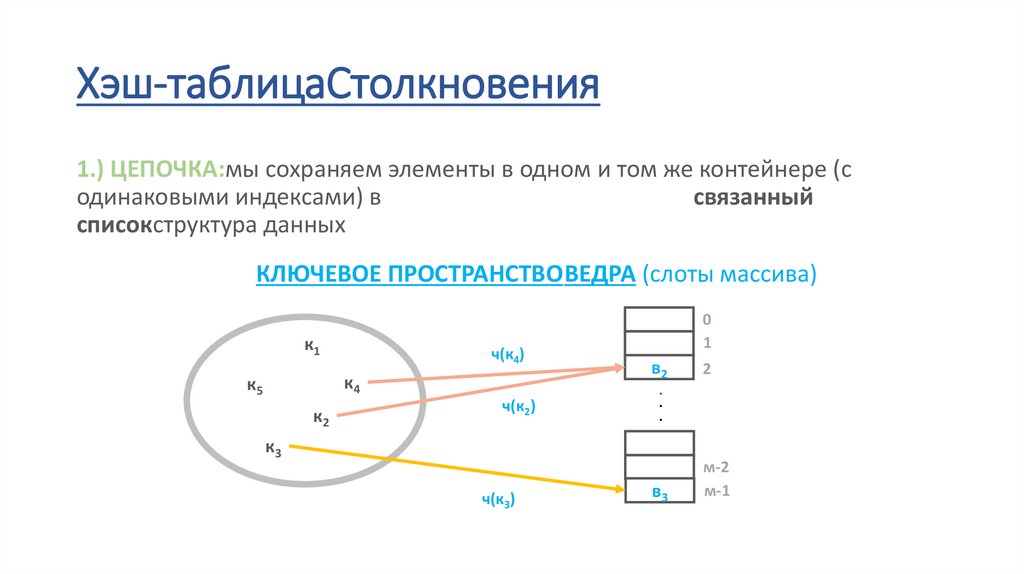
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
к4
к5
к2
к3
2
.
.
.
м-2
м-1
53.
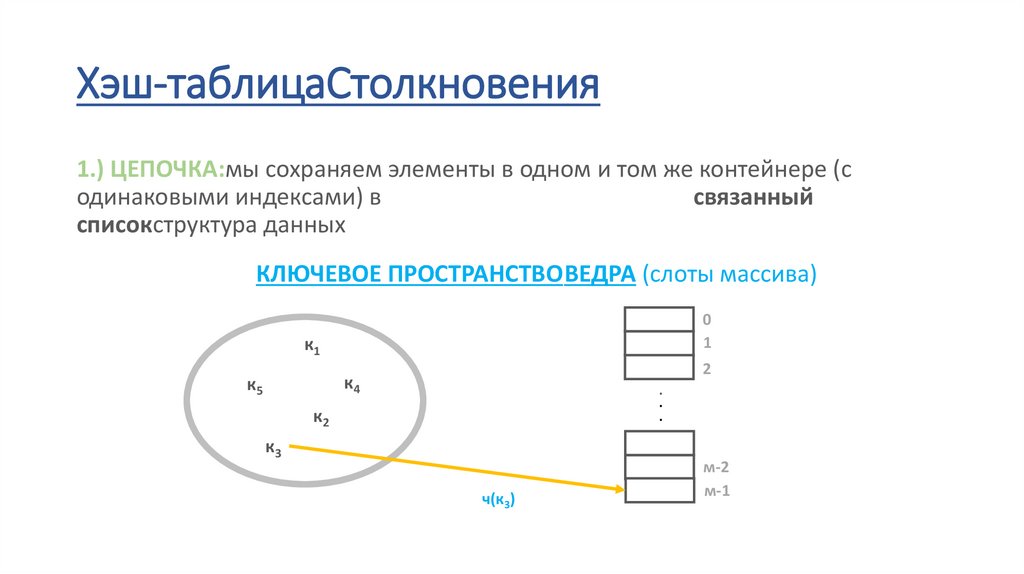
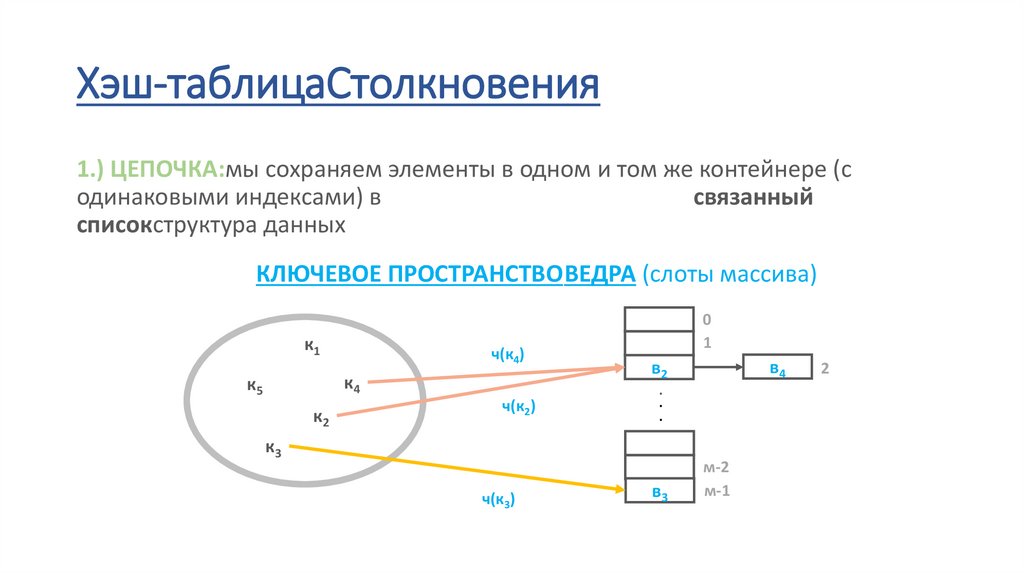
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
.
.
.
к2
к3
ч(к3)
м-2
м-1
54.
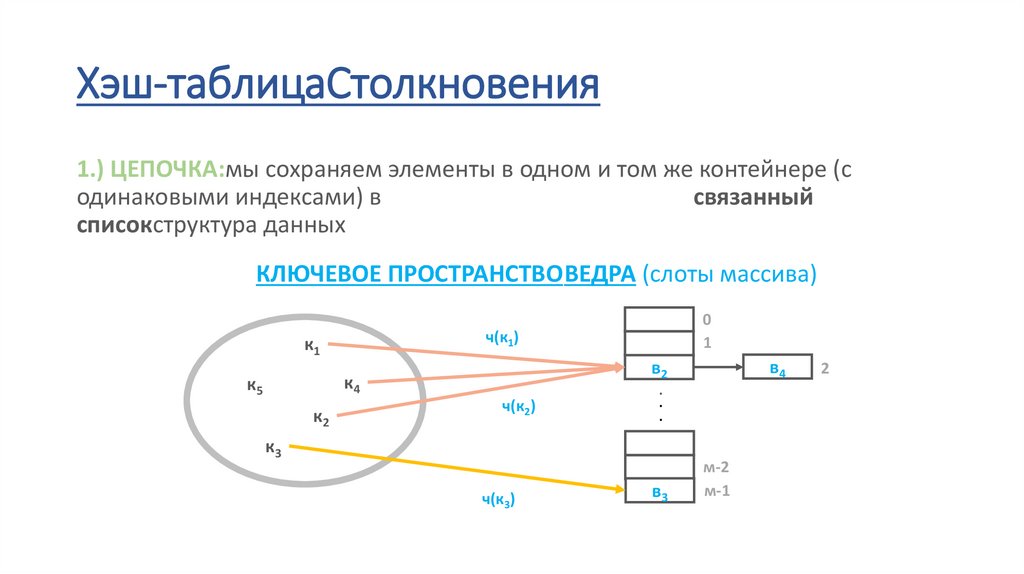
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
.
.
.
к2
к3
ч(к3)
в3
м-2
м-1
55.
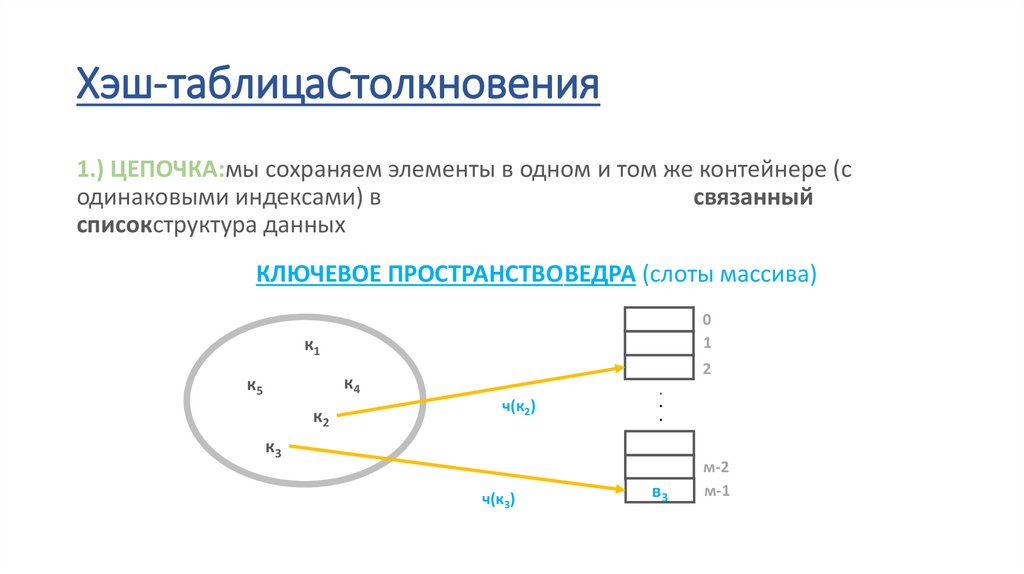
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
к2
ч(к2)
.
.
.
к3
ч(к3)
в3
м-2
м-1
56.
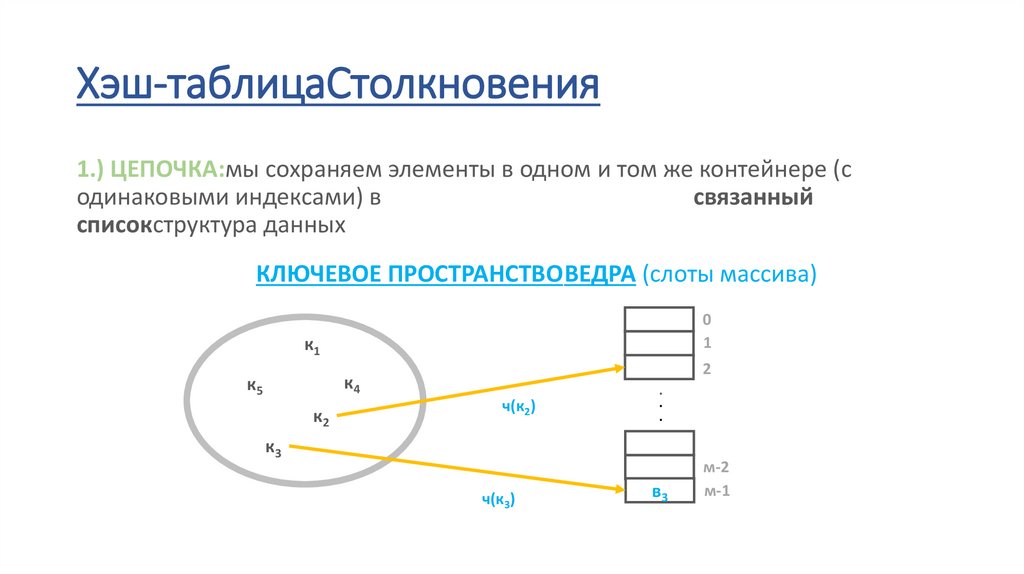
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
к2
ч(к2)
.
.
.
к3
ч(к3)
в3
м-2
м-1
57.
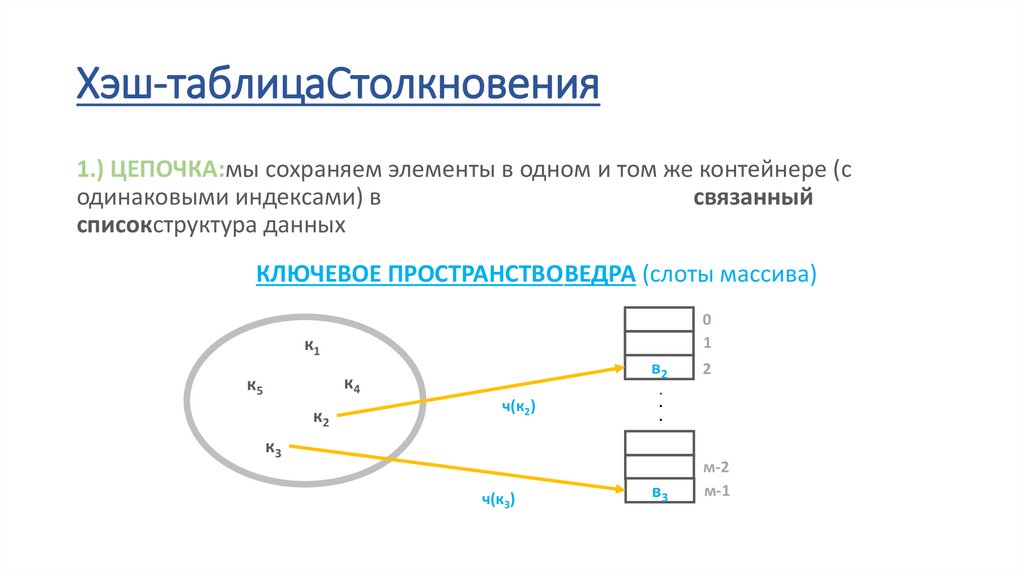
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
к4
к5
к2
ч(к2)
в2
.
.
.
к3
ч(к3)
в3
2
м-2
м-1
58.
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
к1
ч(к4)
к4
к5
к2
ч(к2)
0
1
в2
.
.
.
к3
ч(к3)
в3
2
м-2
м-1
59.
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
к1
ч(к4)
к4
к5
к2
ч(к2)
0
1
к3
ч(к3)
в4
в2
.
.
.
в3
м-2
м-1
2
60.
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
ч(к1)
к1
к4
к5
к2
0
1
ч(к2)
к3
ч(к3)
в4
в2
.
.
.
в3
м-2
м-1
2
61.
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
ч(к1)
к1
к4
к5
к2
0
1
ч(к2)
к3
ч(к3)
в4
в2
.
.
.
в3
м-2
м-1
в1
2
62.
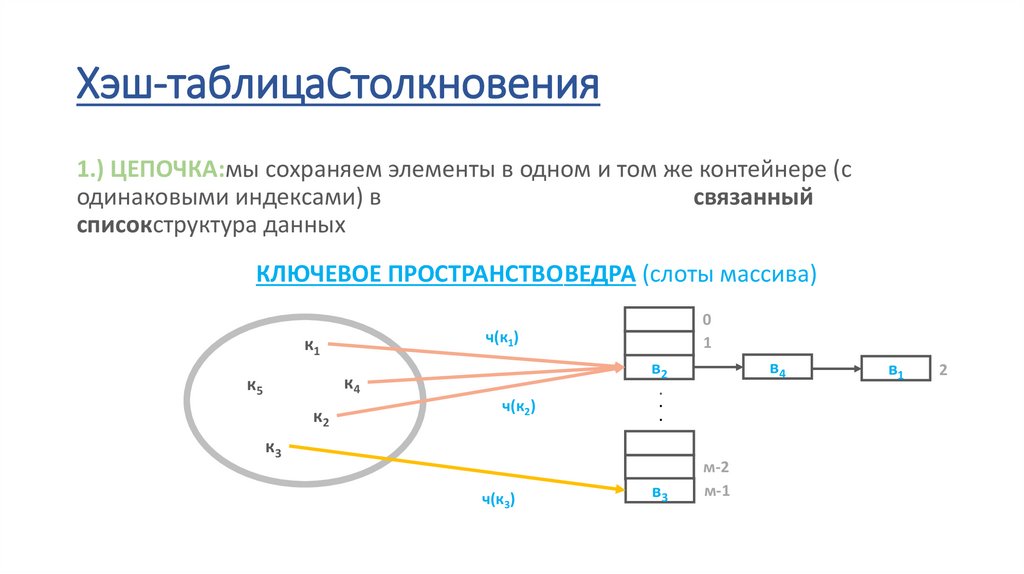
Хэш-таблицаСтолкновения1.) ЦЕПОЧКА:мы сохраняем элементы в одном и том же контейнере (с
одинаковыми индексами) в
связанный
списокструктура данных
в худшем случаеч(х)хэш-функция помещает все элементы
в тот же контейнер (слот массива)
мы получаем связанный список сНА)линейное время
выполнения для большинства
операций
63.
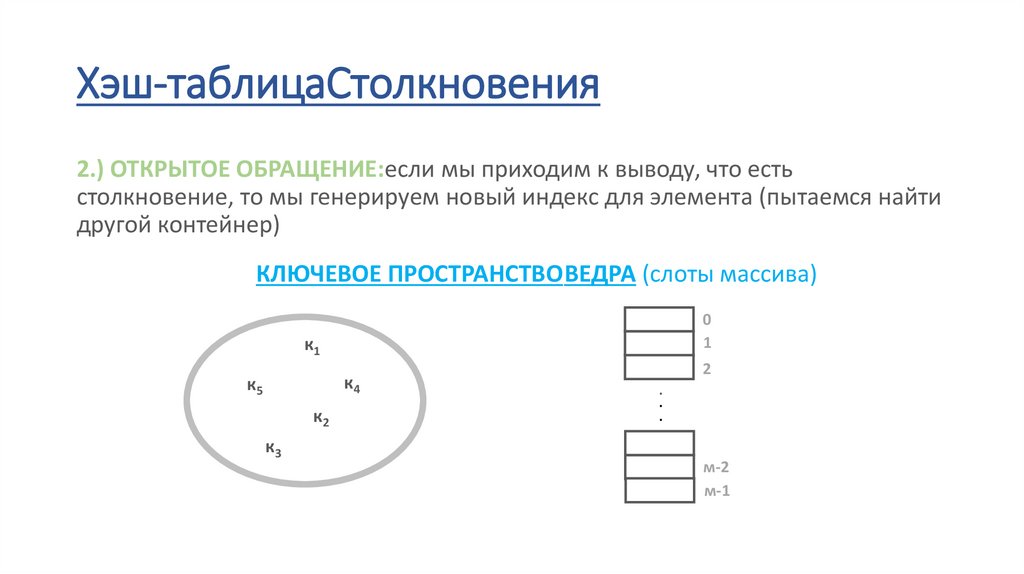
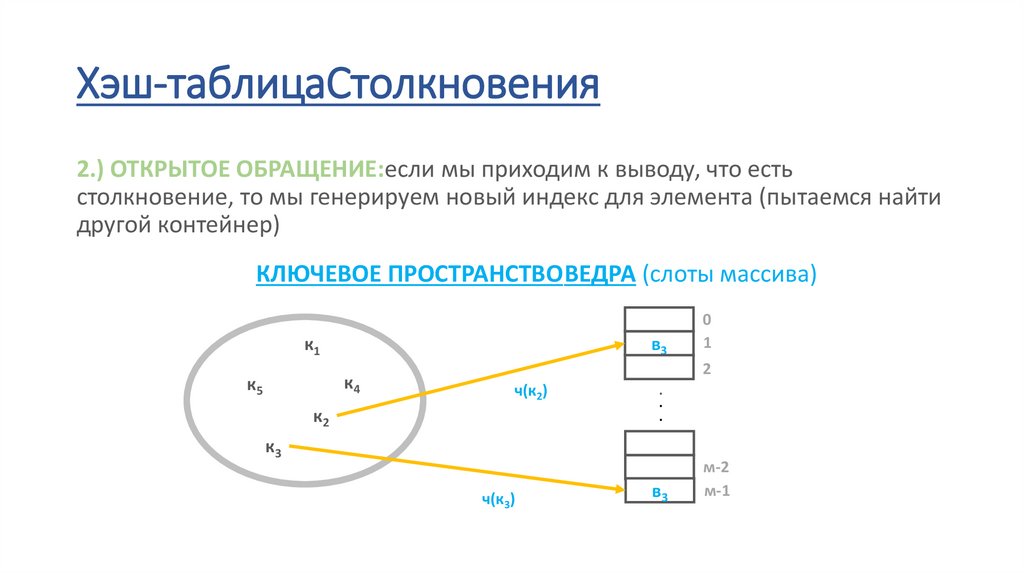
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть столкновение, то
мы генерируем новый индекс для элемента (пытаемся найти другой контейнер)
Линейное зондирование: если столкновение произошло в индексе
массивакзатем
мы пробуем индекск+1,к+2, к+3... пока не найдем пустое ведро
нне всегда является наилучшим возможным вариантом,
поскольку будуткластерыв базовом массиве
ноу него лучшепроизводительность кэшачем другие
подходы
64.
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть столкновение, то
мы генерируем новый индекс для элемента (пытаемся найти другой контейнер)
Квадратичный зонд: если столкновение произошло в индексе
массивакзатем
мы пытаемся добавление последовательных значений
произвольногоквадратичный многочлен
(слоты массива1,4,9,16... в шагах от столкновения)
кластеров не будет (в отличие от линейного зондирования)
но нет преимущества кэширования (элементы находятся
далеко в памяти)
65.
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть столкновение, то
мы генерируем новый индекс для элемента (пытаемся найти другой контейнер)
Перефразирование: если столкновение произошло в индексе
массивакзатем
мы используемч(х)снова хэш-функция для генерации нового
индекса
66.
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
к4
к5
к2
к3
2
.
.
.
м-2
м-1
67.
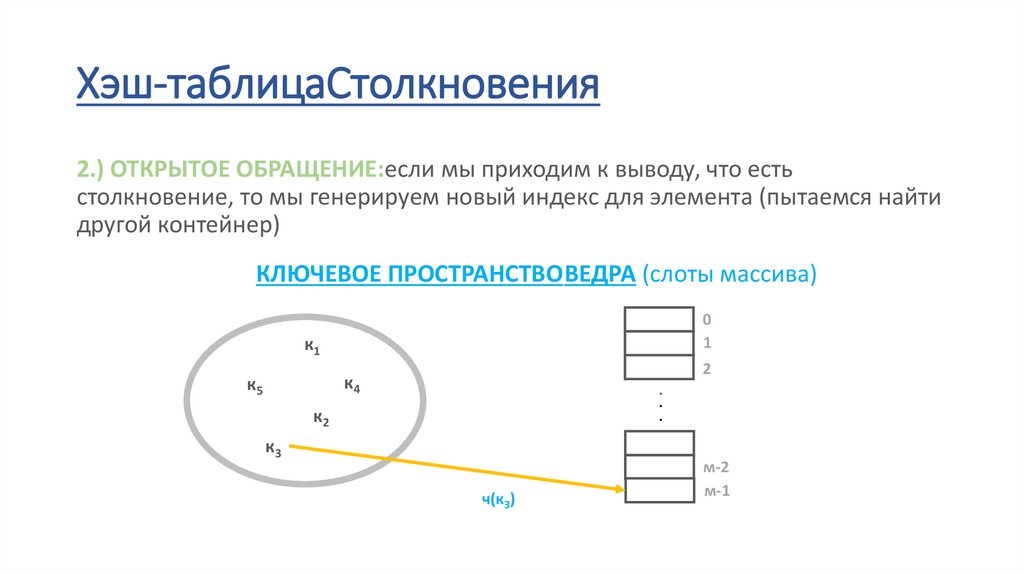
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
.
.
.
к2
к3
ч(к3)
м-2
м-1
68.
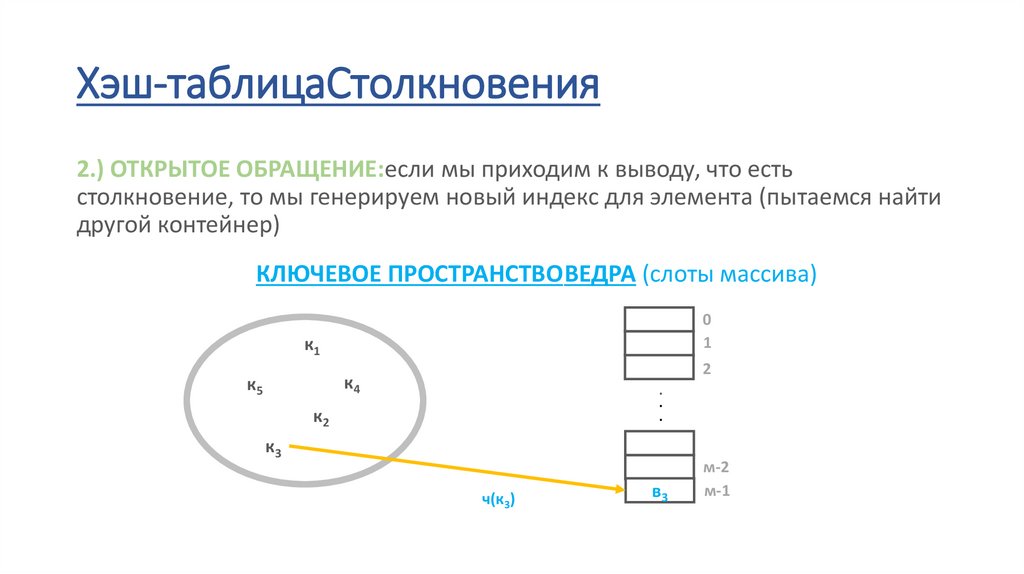
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
2
к4
к5
.
.
.
к2
к3
ч(к3)
в3
м-2
м-1
69.
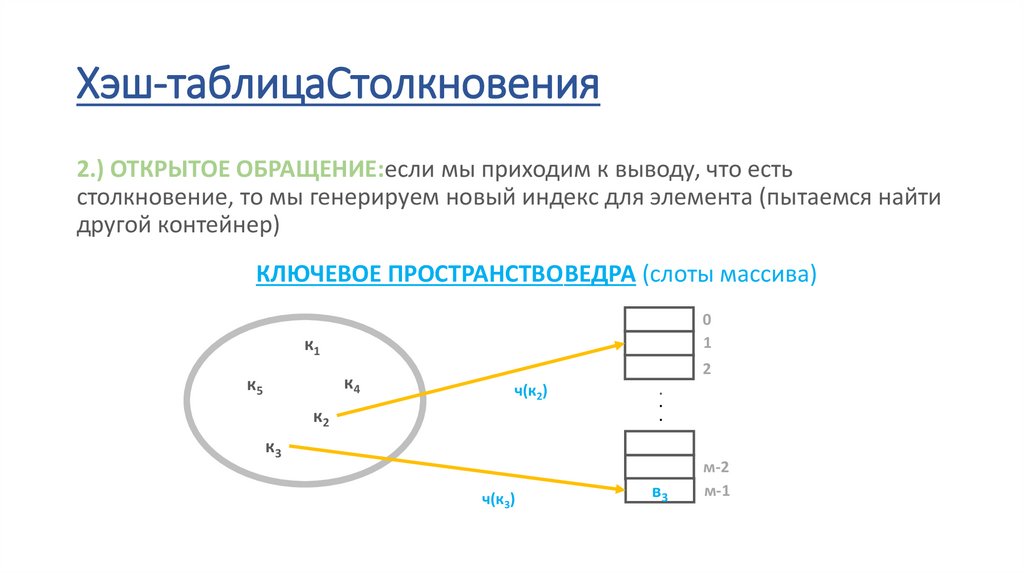
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
0
1
к1
к4
к5
2
ч(к2)
к2
.
.
.
к3
ч(к3)
в3
м-2
м-1
70.
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
в3
к1
к4
к5
0
1
2
ч(к2)
к2
.
.
.
к3
ч(к3)
в3
м-2
м-1
71.
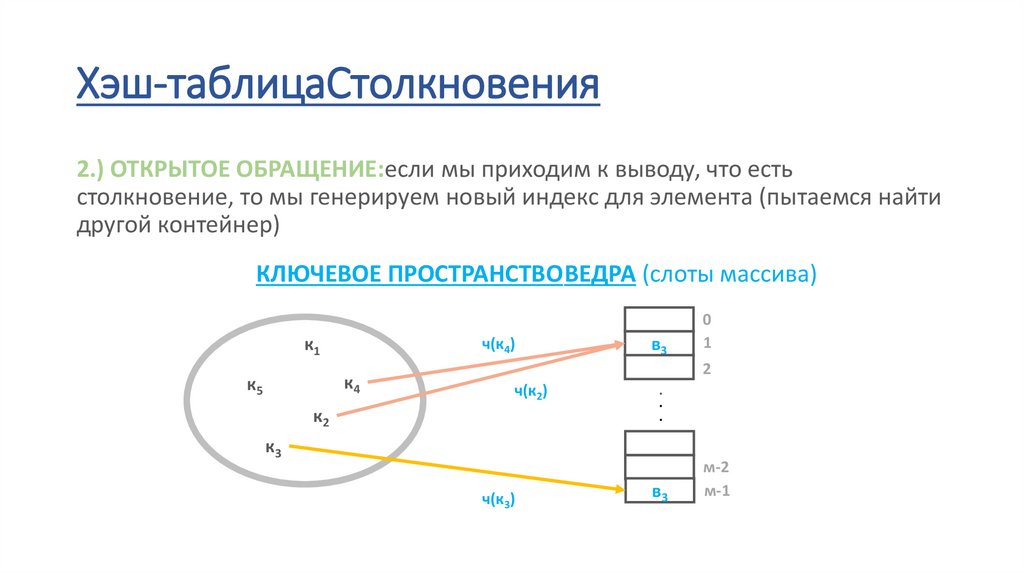
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
к1
ч(к4)
к4
к5
в3
0
1
2
ч(к2)
к2
.
.
.
к3
ч(к3)
в3
м-2
м-1
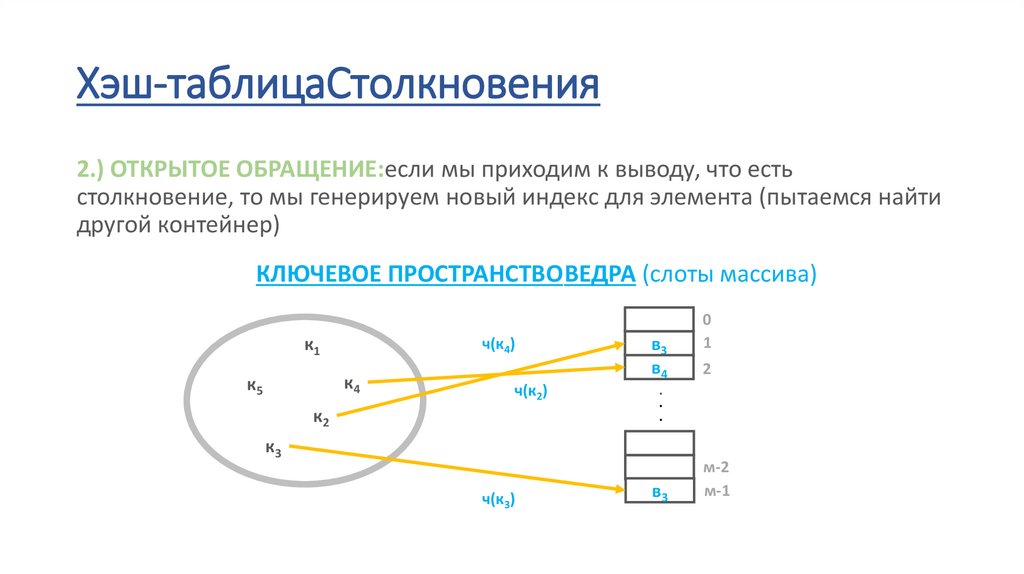
72.
Хэш-таблицаСтолкновения2.) ОТКРЫТОЕ ОБРАЩЕНИЕ:если мы приходим к выводу, что есть
столкновение, то мы генерируем новый индекс для элемента (пытаемся найти
другой контейнер)
КЛЮЧЕВОЕ ПРОСТРАНСТВОВЕДРА (слоты массива)
к1
ч(к4)
к4
к5
ч(к2)
к2
в3
в4
.
.
.
к3
ч(к3)
в3
0
1
2
м-2
м-1
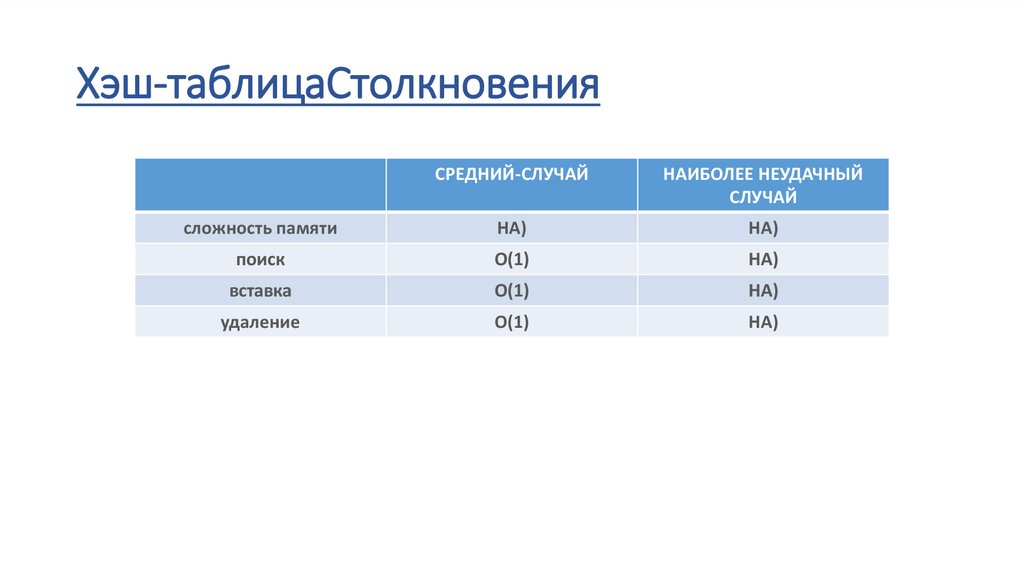
73.
Хэш-таблицаСтолкновенияСРЕДНИЙ-СЛУЧАЙ
НАИБОЛЕЕ НЕУДАЧНЫЙ
СЛУЧАЙ
сложность памяти
НА)
НА)
поиск
О(1)
НА)
вставка
О(1)
НА)
удаление
О(1)
НА)
74.
Динамическое изменениеразмера
(Алгоритмы и структуры
данных)
75.
Фактор нагрузки• the р(х)вероятность столкновения не является постоянной
• чем больше элементов в хеш-таблице, тем выше p(x)вероятность
столкновения
• вот почему нам нужно определить новый параметр хеш-таблицы
– так называемыйкоэффициент нагрузки














































 Информатика
Информатика








