Структуры и алгоритмы обработки данных. Сортировка массивов

1.

Структуры и Алгоритмы
Обработки Данных
СОРТИРОВКА МАССИВОВ
1

2.

Понятие сортировки
Сортировка — процесс получения упорядоченного
массива.
Процесс – последовательность
состояний чего-либо.
стадий
или
Массив в котором для любого ai элемента значение
его ключа не больше (не меньше) чем значение ключа
ai+1-го элемента называется упорядоченным по
возрастанию (по убыванию).

3.

ФОРМУЛИРОВКА ЗАДАЧИ
Исходные данные ― неупорядоченный или частично
упорядоченный массив A[a1, a2, …,an], состоящий
из n элементов.
Цель ― получить упорядоченный массив
(по возрастанию/убыванию значения ключа).
Результат ― упорядоченный массив.
3

4.

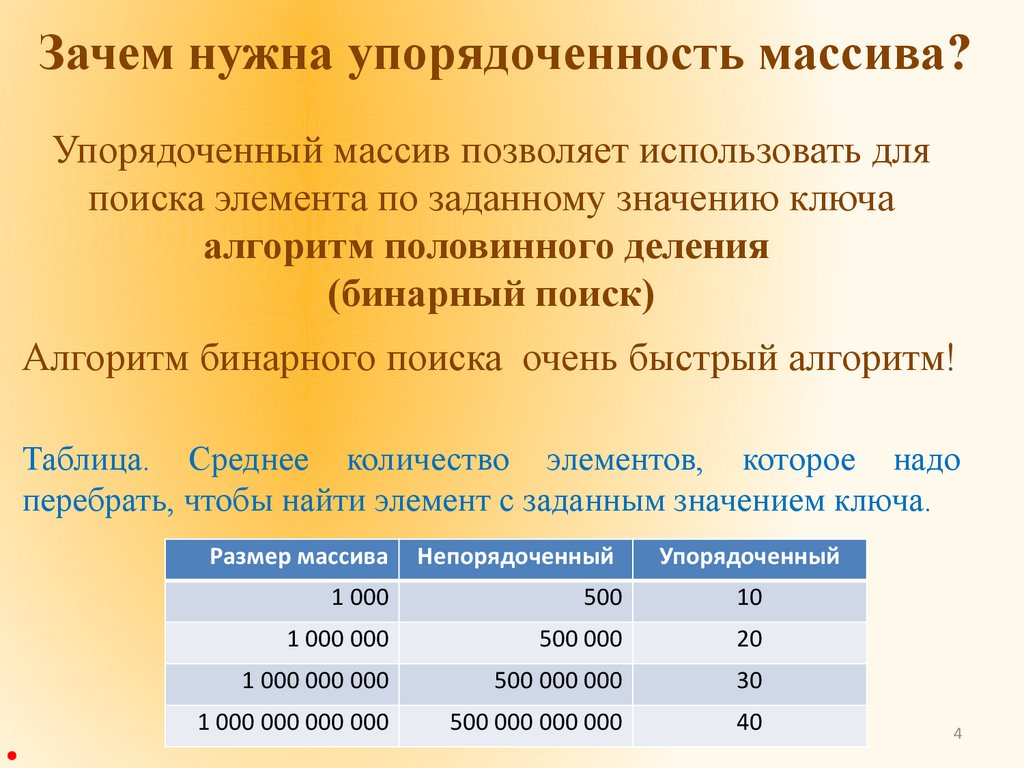
Зачем нужна упорядоченность массива?
Упорядоченный массив позволяет использовать для
поиска элемента по заданному значению ключа
алгоритм половинного деления
(бинарный поиск)
Алгоритм бинарного поиска очень быстрый алгоритм!
Таблица. Среднее количество элементов, которое надо
перебрать, чтобы найти элемент с заданным значением ключа.
Размер массива
Непорядоченный
Упорядоченный
1 000
500
10
1 000 000
500 000
20
1 000 000 000
500 000 000
30
1 000 000 000 000
500 000 000 000
40
4

5.

Зачем нужна упорядоченность массива?
1. В упорядоченном массиве можно использовать
быстрый алгоритм бинарного поиска элемента по
заданному значению ключа.
2. По различным оценкам применимости в практике
различных структур данных частота использования
массива – 80-90%.
3. Если массив упорядочен по одному ключу, а надо
работать по другому ключу, то для достижения
упорядоченности его надо сортировать.
Эти факторы определи практическую
необходимость разработки целого семейства
алгоритмов сортировки массива.
5

6.

ПОЧЕМУ СЕМЕЙСТВО АЛГОРИТМОВ?
Вопрос: Зачем семейство алгоритмов?
Почему не выбрать ОДИН ЛУЧШИЙ алгоритм?
Ответ: Скорость выполнения сортировке ВСЕХ
разработанных
быстродействующих
алгоритмов
зависит от начального состояния сортируемого
массива.
Различают три начальных состояния массива
относительно значений ключа:
1. Элементы расположены случайным образом.
2. Элементы расположены упорядочены или близки к
требуемому упорядоченному положению.
3. Элементы расположены упорядочены или близки к
упорядоченному
положению
в
обратном
6
направлении.

7.

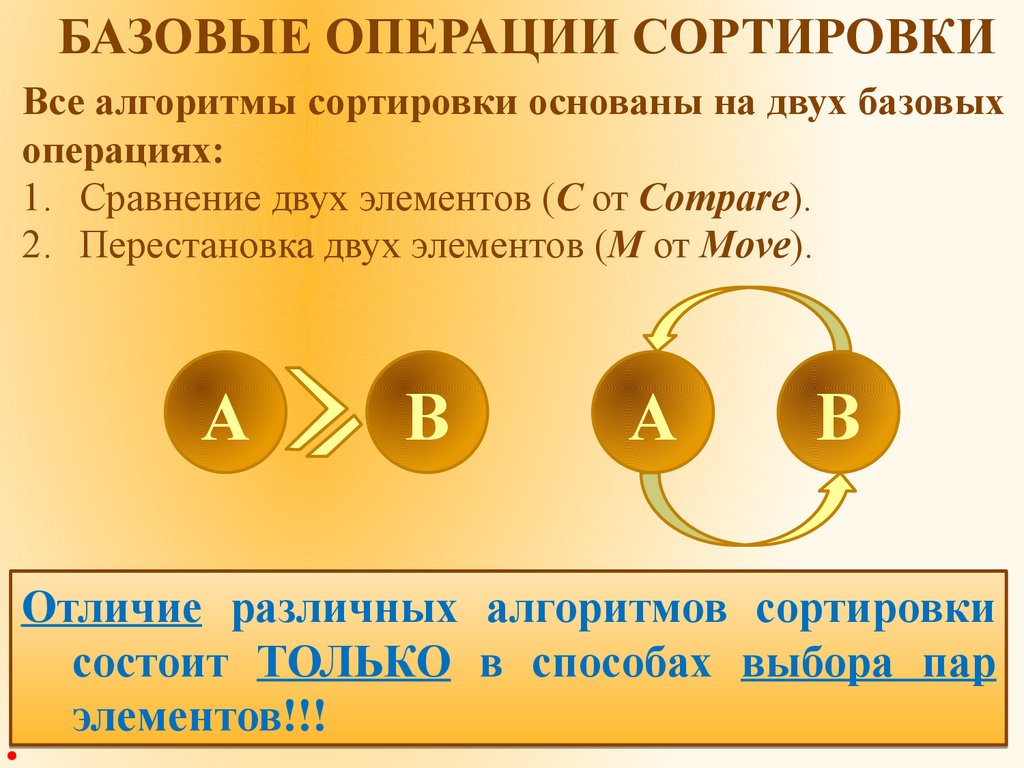
БАЗОВЫЕ ОПЕРАЦИИ СОРТИРОВКИ
Все алгоритмы сортировки основаны на двух базовых
операциях:
1. Сравнение двух элементов (С от Compare).
2. Перестановка двух элементов (M от Move).
А
В
А
В
Отличие различных алгоритмов сортировки
состоит ТОЛЬКО в способах выбора пар
элементов!!!
7

8.

Алгоритм сортировки
простым выбором
Алгоритм сортировки простым выбором прост для
понимания и реализации.
Его идея основана на разделении массива на две части:
• уже упорядоченную;
• и еще не упорядоченною.
На каждом шаге алгоритм определяет элемент в
минимальным значение в неупорядоченной области и
переносит его в упорядоченную.
Эта идея лежит в основе всех простейших алгоритмов.

9.

Алгоритм сортировки
простым выбором
1. Разделитель между упорядоченной и неупорядоченной часть
устанавливается перед первым элементом.
2. Ищется минимальный элемент в неупорядоченной части.
3. Найденный элемент с наименьшим значением меняется
местами с первым неупорядоченным элементом.
4. Разделитель сдвигается на 1 элемент в право.
5. Если разделитель не вышел за пределы массива переход к п.2
6. Иначе – конец алгоритма.
21543
Упорядоченные
элементы
Неупорядоченные
элементы
9

10.

Алгоритм сортировки
простым выбором
Скорость
сортировки
алгоритмом
простым выбором пропорциональна
~n
2
Оценка скорости:
n итераций по массиву и n/2 в среднем
проходов по неупорядоченной части
массива.
10

11.

Алгоритм сортировки простыми
включениями
1. Разделитель P устанавливается после первого элемента.
P=1.
2. Обрабатываемый элемент a(P) копируется в
вспомогательную переменную (T): T=a(P) - первый элемент
после разделителя.
3. В цикле движущимся от разделителя к началу массива
последовательно сравниваются a(i) начиная a(P-1) с
элементом T.
3.1 Если T< a(i) a(i) элемент сдвигается на 1 элемент
вправо: a(i+1)= a(i). Переход к п.3.
3.2 Если T>= a(i)
3.2.1 a(i+1)= T - элемент помещается в упорядоченную
часть массива.
3.2.2 Если P=n-1 завершение алгоритма.
11
3.2.3 Иначе P=P+1. Переход к п.2

12.

Алгоритм сортировки простыми
включениями
Алгоритм тоже основан на принципе разделения массива на две
части ― упорядоченную и неупорядоченную.
21543
Упорядоченные
элементы
Неупорядоченные
элементы
Быстродействие алгоритма так же как и
предыдущего оценивается пропорциональным
~n
2
12

13.

Алгоритм сортировки пузырьком
(по возрастанию значения ключа)
Является одним из простейших и широко известным
алгоритмом сортировки .
1. Просматриваются подряд все рядом расположенные
пары элементов от начала массива до конца, от a[0]
до a[n-1] (итерация).
2. Если a[i] > a[i+1] – элементы меняются местами.
Если a[i] <= a[i+1] – элементы остаются на местах.
3. После n-1 итераций массив упорядочен.

14.

Пример сортировки пузырьком
(АНИМАЦИЯ)
Второй
Первый проход:
Третий
проход:
21543
С=4
M=0
3
1
! Если на очередном проходе в методе пузырька не сделано
ни одной перестановки, то процесс сортировки можно
прервать т.к.массив УПОРЯДОЧЕН.
Алгоритм сортировки пузырьком,
называется усовершенствованным
пузырьком.
который использует это
алгоритмом сортировки
Но все равно в большинстве случаев его быстродействие
~n
2
Выигрыш по быстродействию возможен только в случаях если
исходный массив упорядочен или близок к упорядоченному.
14

15.

Общая идея ускоренных алгоритмов
!
Идея всех «ускоренных» алгоритмов состоит в том,
чтобы на каждом шаге постараться переместить
элемент не на одну позицию, а на несколько.
Во всех алгоритмах, рассмотренных ранее, каждый
элемент сравнивался и менялся местами либо с
предыдущим, либо со следующим элементом.
a. В алгоритме Шелла идея перемещения элементов на
несколько позиций осуществляется посредством деления на
группы.
b. В алгоритме быстрой сортировки данная идея реализована
путем разделения на каждом шаге массива на два подмассива
так, что все элементы одного подмассива меньше, чем все
элементы второго.
15

16.

АЛГОРИТМ СОРТИРОВКИ ШЕЛЛА
1. Массив a[n] разбивается на ki групп.
1 группа a[0], a[ki], a[2*ki], a[3*ki], …
2 группа a[1], a[ki+1], a[2*ki+1], a[3*ki+1], …
3 группа a[2], a[ki+2], a[2*ki+2], a[3*ki+2], …
……………………………………………………
ki группа a[ki-1], a[2*ki-1], a[3*ki-1], a[4*ki-1], …
2. Внутри каждой группы производится сортировка
каким-либо
простым
алгоритмом,
например,
пузырьком.
3. Если ki = 1 Завершение алгоритма.
4. i увеличивается на 1 и выбирается ki < ki-1. Переход к
пункту 1.
16

17.

Пример алгоритма сортировки Шелла
Быстродействие алгоритма зависит от ряда факторов и в
зависимости от выбранных значений в литературе
приводятся разные оценки. Вот наиболее популярные:
О(n )
O(n )
3/2
O(n*log n)
4/3
2
k =1:
=3:
=5:
1
2
3
14
25
31
12
2
3
3
4
1
5
28 32 74 52 11 7 98 36 29 41
17
17

18.

АЛГОРИТМ СОРТИРОВКИ ШЕЛЛА
(выбор количества групп)
Возникает вопрос:
Разбиение на какое количество групп оптимально?
Эмпирически
показано,
что
хорошими
последовательностями количества групп являются
последовательности, описываемые формулами:
ki = 3*l+1
ki = 2*l+1,
где:
ki ― количество групп,
l ― натуральное число.
Соответственно это следующие последовательности:
1,4,7,11…
либо 1,3,5,7,…
18

19.

АЛГОРИТМ БЫСТРОЙ СОРТИРОВКИ
1. Выбирается пороговое значение (ПЗ).
2. Запускается процесс P1 просмотра элементов массива сверхувниз.
2.1 Если aip1 < ПЗ переход к aip1+1
2.2 Иначе – приостановка Р1.
3. Запускается процесс P2 просмотра элементов массива снизувверх.
3.1 Если aip2 > ПЗ переход к aip2-1
3.2 Иначе – приостановка Р2.
4. Элементы aip1 и aip2 меняются местами.
5. Переход к пункту 2. с места приостановки процессов Р1 и Р2.
6. Процесс выполнения пунктов 2-5 продолжаются пока
процессы Р1 и Р2 не встретятся.
19

20.

АЛГОРИТМ БЫСТРОЙ СОРТИРОВКИ
В результате проведенных действий массив разделён на две части
в месте встречи процессов Р1 и Р2.
Конечно он не упорядочен!
Но массив приобрел существенное новое свойство:
• Все элементы верхней части меньше порогового значения.
• Все элементы нижней части больше порогового значения.
Значит в результирующем упорядоченном массиве:
• Ни один элемент из верхней части не перейдет в нижнюю.
• Ни один элемент из нижней части не перейдет в верхнюю.
И мы можем сортировать каждую часть
независимо от другой!
20

21.

АЛГОРИТМ БЫСТРОЙ СОРТИРОВКИ
Тогда запускаем этот же алгоритм отдельно на каждую из
частей.
Получаем 4 отдельных части массива с теми же свойствами –
ни один элемент каждой части не перейдет в упорядоченном
массиве в другую часть.
Продолжим такие действия для каждой из появляющихся
частей до тех пор, пока каждая из них не станет размером 1
элемент.
После завершение алгоритма – массив УПОРЯДОЧЕН!!!
Быстродействие алгоритма оценивается как
O(n log n)
21

22.

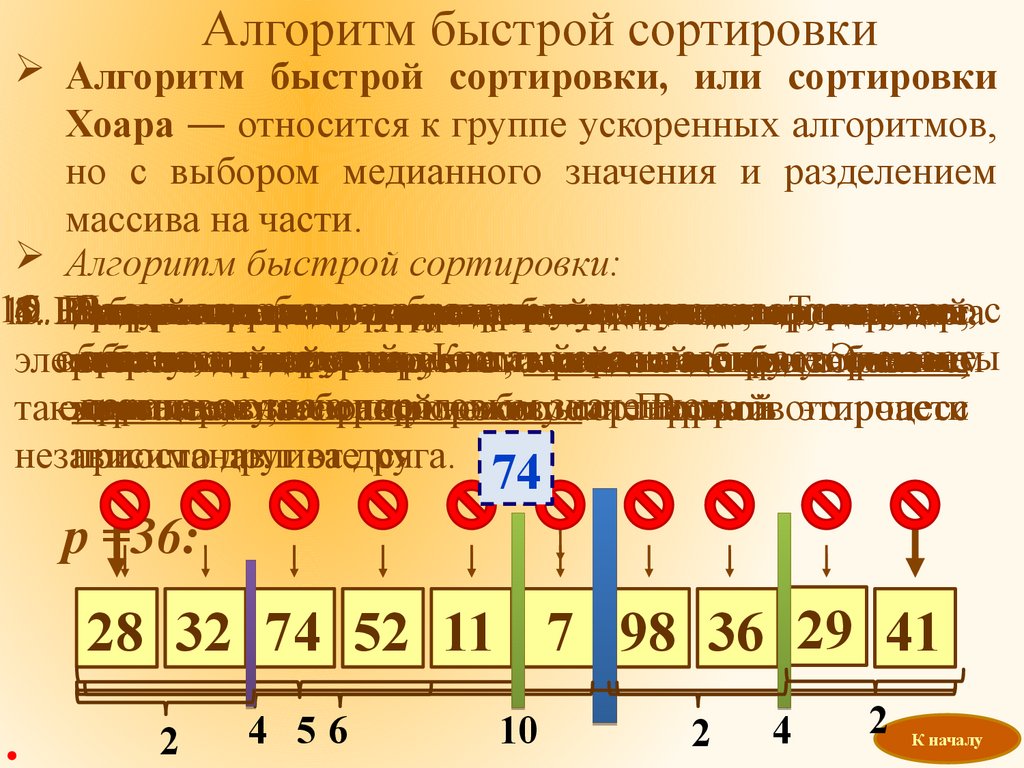
Алгоритм быстрой сортировки
Алгоритм быстрой сортировки, или сортировки
Хоара ― относится к группе ускоренных алгоритмов,
но с выбором медианного значения и разделением
массива на части.
Алгоритм быстрой сортировки:
11.
2. Выбирается
5.
9.
Левая
Далее
Элементы,
Запускаются
часть
подобным
массива
насортировка
поочередно
которых
образом
теперь
приостановлены
сортируются
два
упорядочена.
процесса:
поочередно
Таким
процессы,
же
– с
1.
пороговое
значение.
10.
8.
6.
4.
3.
7.
В
Процессы
Второй
Разделение
В
Теперь
первом
окончательно
процесс,
массив
процессе
продолжают
инекоторое
разделен
запускаемый
упорядоченном
сравнения
работу
происходят
на
происходят
сдве
до
конца,
массиве
тех
части:
допор,
тех
продолжает
до
ни
пор,
водин
тех
пока
левой
один
пор,
пока
не
образом
начала,
меняются
обе
части
иместами.
другой
и–Каждый
оставшаяся:
с перейдет
конца
массива.
выбирается
Элементы
новое
элемент
количество
встретятся.
работу
пока
расположены
не
изсортируется
найдется
до
левой
вмассива.
тех
сортируемом
части
значения
пор,
элемент,
не
пока
значение
массиве
меньшие
неразнайдется
которого
внеправую
или
будет
значение,
больше
равные
равным
часть,
сравниваются
пороговое
значение.
с пороговым
значением.
также
единице.
меньшее,
или
пороговому,
как равно
и наоборот,
вчем
правой
пороговому.
пороговое.
можно
— большие
сортировать
Первый
порогового.
Второй эти
процесс
части
независимо
приостанавливается.
друг от друга.
36
32
11
29
52
41
74
7
р =36:
28 32 74 52 11 7 98 36 29 41
2
4 56
10
2
4
2
22
К началу

23.

ВЫБОР ПОРОГОВОГО ЗНАЧЕНИЯ
o Медианное значение ― такое значение порогового
числа при котором половина значений массива будут
меньше него, а другая половина ― больше.
40,8
11
7
36
29
28
74
52
98
41
! Медианное значение может по значению не совпадать со
значением ни одного из элементов.
В алгоритме быстрой сортировки эффективность
зависит от выбора порогового значения.
Существует несколько способов выбора порогового
значения, и одним из оптимальных является
принятие за пороговое медианного значения.
23

24.

ВЫЧИСЛИТЕЛЬНАЯ МОЩНОСТЬ
!
За меру скорости алгоритма принято количество
сравнений и перестановок в алгоритмах.
Однако для обозначения быстродействия алгоритмов
наиболее
часто
используется
понятие
«вычислительная мощность».
Алгоритм сортировки
Сортировка пузырьком
Сортировка простым выбором
Сортировка простыми включениями
Быстрая сортировка
Сортировка Шелла
Лучшее время
O(n²)
O(n²)
O(n2)
O(n log n)
O(n log2 n)
24

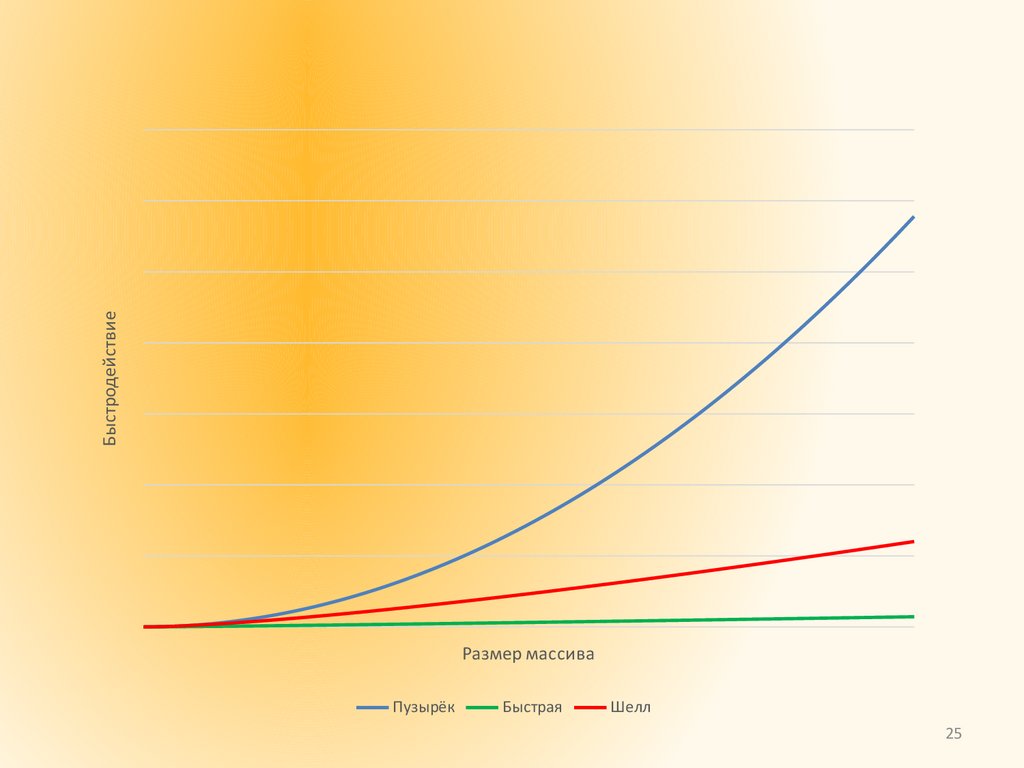
25.

Быстродействие
Размер массива
Пузырёк
Быстрая
Шелл
25

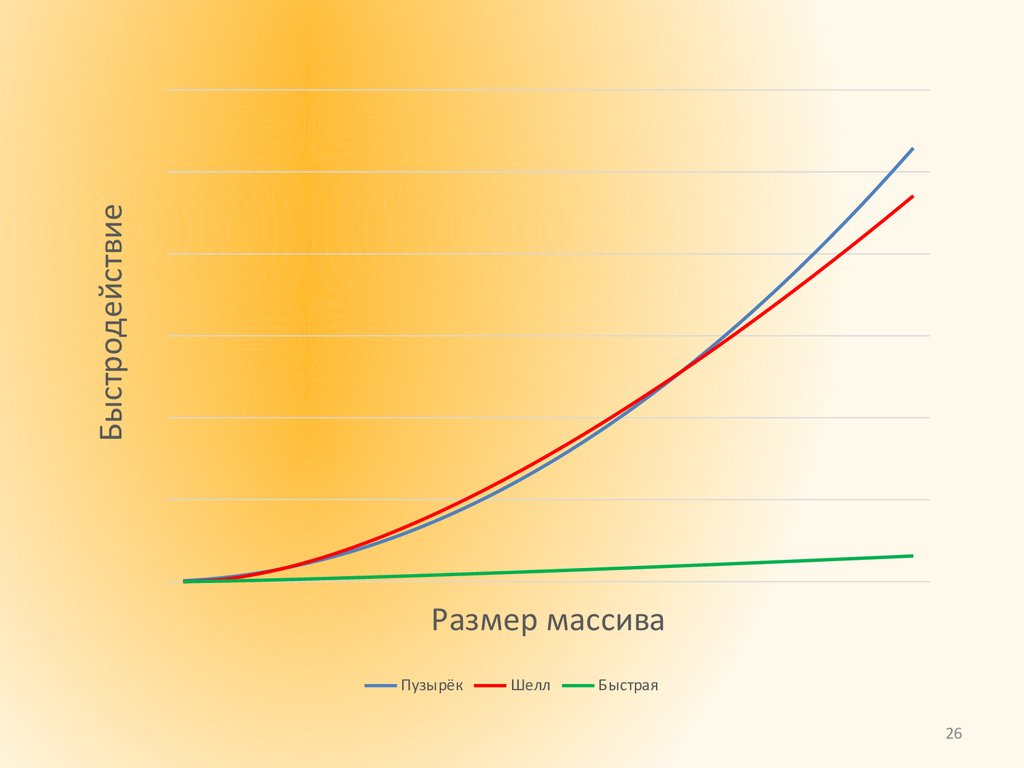
26.

Быстродействие
Размер массива
Пузырёк
Шелл
Быстрая
26

27.

Поразрядная (битовая) сортировка
Идея поразрядной сортировки отличается от идей
алгоритмов, которые рассматривали выше.
Поразрядная сортировка использует операцию
перестановку элемента, но не использует операции
сравнения значения ключа как одного целого.
Анализируется не значение ключа как одного целого, а
его фрагменты - разряды ключа.
Запись любого значения состоит из ограниченного
количества символов некоторого алфавита.
В данной области отдельный символ именуется
разрядом записи.
27

28.

Поразрядная (битовая) сортировка
До сортировки необходимо знать два параметра ключа:
• m - разрядность данных: количество возможных
значений разряда ключа;
• k - количество разрядов в самом длинном ключе.
При сортировке русских слов m = 33.
Пусть в самом длинном слове 10 букв, k = 10.
При сортировке целых десятичных m = 10.
Если числа от 0 до 1000 00010 k = 7.
При сортировке целых шестнадцатиричных m = 16.
Если числа от 0 до FFF FFF16 k = 6.
28

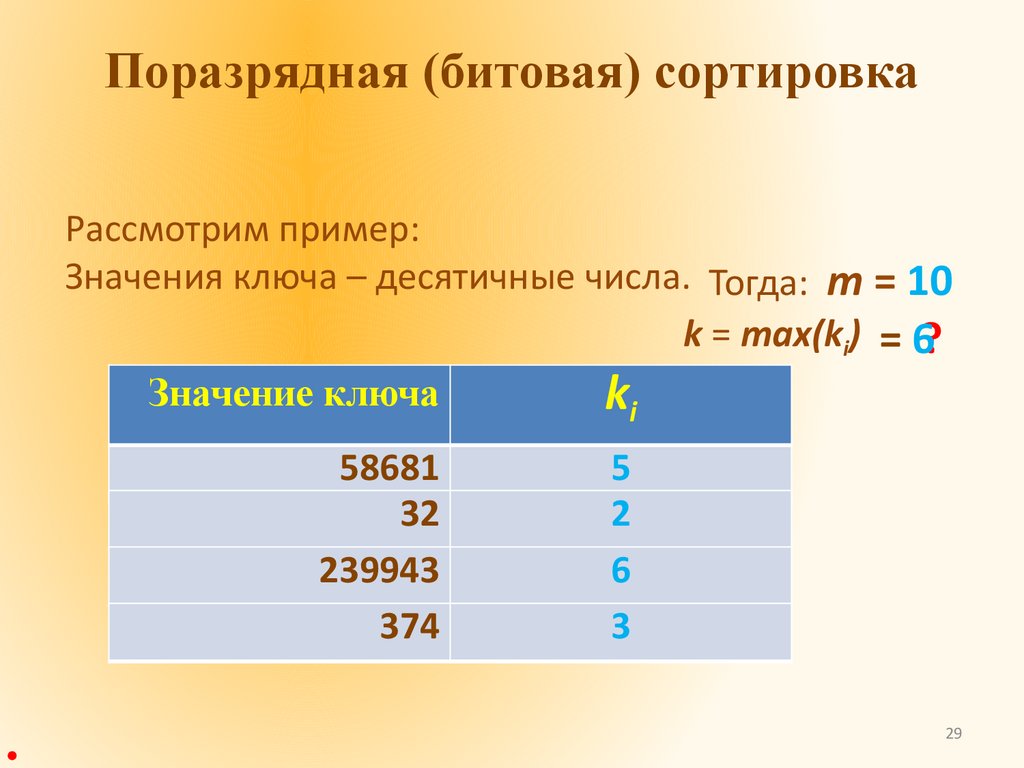
29.

Поразрядная (битовая) сортировка
Рассмотрим пример:
Значения ключа – десятичные числа. Тогда: m = 10
k = max(ki) = 6?
Значение ключа
ki
58681
32
239943
374
5
2
6
3
29

30.

Поразрядная (битовая) сортировка
Алгоритм разделяется на две фазы:
1. Фаза распределения.
2. Фаза сборки.
Фаза распределения
1. Вводится переменная номер разряда Npos = k.
2. Создается m связных списков.
3. Списки очищаются.
4. Просматриваются все сортируемые элементы и по
значению Npos разряда помещаются в
соответствующий список.
30

31.

Поразрядная (битовая) сортировка
Фаза сборки
1. Все списки начиная с первого до последнего
последовательно соединяются.
2. Npos = Npos - 1
3. Если Npos равно 0 завершение алгоритма.
Иначе снова выполняется фаза распределения и
фаза сборки.
31

32.

Поразрядная (битовая) сортировка
Пример 56 38 19 7 72
k
0
1
2 72
3 3
4
5
6 56
7
18
8
9
18
3
7
38
19
32

33.

Поразрядная (битовая) сортировка
Пример 72 3 56 7 38 18 19
k
0
1
2
3
4
5
6
7
8
9
3
7
18
19
38
72
56
33

34.

Поразрядная (битовая) сортировка
Поразрядная сортировка требует
дополнительную память!
Поразрядную сортировку эффективно
реализовывать связным списком
Вычислительная мощность
поразрядной сортировки
O(n)
34

35.

СОРТИРОВКА БОЛЬШИХ МАССИВОВ
Алгоритм слияния
1. Массив размером N разбивается на два равных по размеру
файла файла A и B.
2. Вводится переменная GroupSize = 1 – размер сортируемой
подгруппы.
3. Вводится переменная i = 0 – индекс обрабатываемой
подгруппы элементов.
4. Создаётся пустой файл C.
5. Создается счетчик количество элеменв
6. Создаются две переменные jA = 0 и jB = 0 – счетчики
просмотренных элементов в группах. Счетчики меняют свои
значения от 0 до GroupSize.
35

36.

СОРТИРОВКА БОЛЬШИХ МАССИВОВ
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
Если jA = < GroupSize читается A[i] - очередное значение группы
из файла A.
Если jB = < GroupSize читается B[i] - очередное значение группы
из файла B.
Если jA < GroupSize и A[i] jA < B[i] jB в С записывается A[i] jA.
Счетчик jA увеличивается на 1. Переход к пункту 6.
Если jB < GroupSize и A[i] jA > B[i] jB в С записывается B[i] jB.
Счетчик jB увеличивается на 1. Переход к пункту 6.
Если jA >= GroupSize и jB >= GroupSize – Конец обработки
группы.
Если GroupSize > Log2N. Файл С содержит упорядоченный
массив.
Конец алгоритма.
Иначе GroupSize = 2 * GroupSize.
Файл С разбивается на два файла А и В. Переход к пункту 3.
36
Переход к пункту 6.

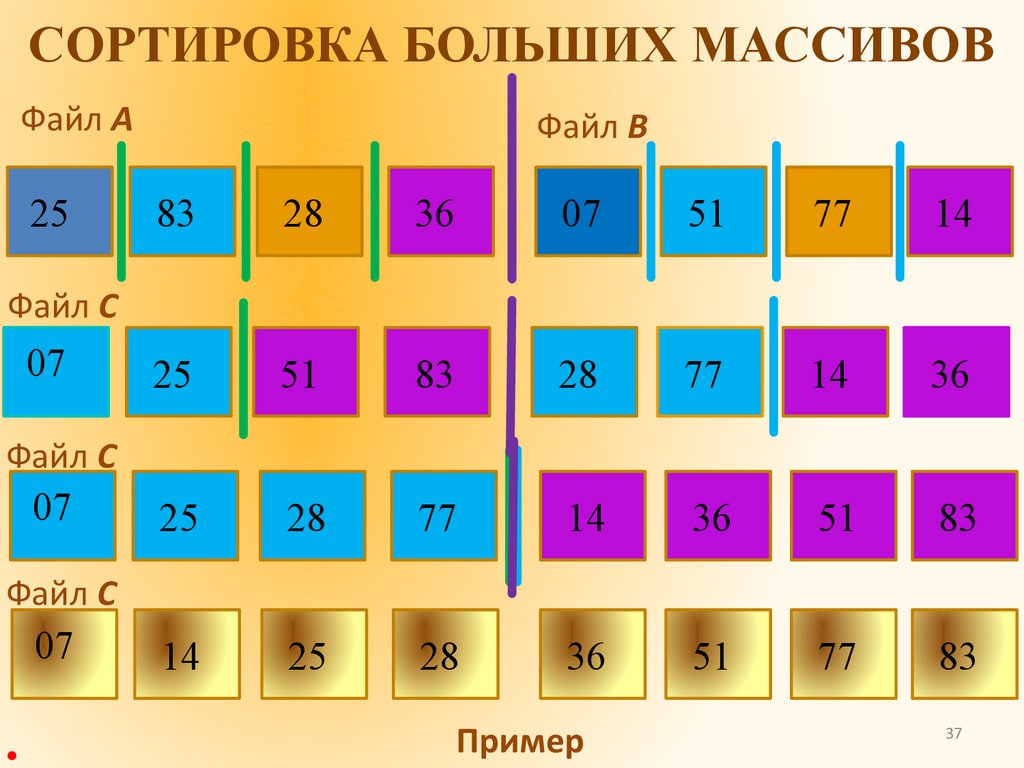
37.

СОРТИРОВКА БОЛЬШИХ МАССИВОВ
Файл А
25
Файл В
83
28
36
07
51
77
14
25
51
83
28
77
14
36
25
28
77
14
36
51
83
14
25
28
36
51
77
83
Файл С
07
Файл С
07
Файл С
07
Пример
37

38.

Алгоритмы сортировки
Алгоритмы сортировки массивов, изучаемые в
данном курсе:
1. Алгоритм сортировки пузырьком;
2. Алгоритм сортировки простым выбором;
3. Алгоритм сортировки простыми включениями;
4. Алгоритм сортировки Шелла;
5. Алгоритм быстрой сортировки.
38

39.

КРИТЕРИИ ВЫБОРА
АЛГОРИТМА СОРТИРОВКИ
Выбор алгоритма сортировки
производится согласно следующим
критериям:
Скорость выполнения алгоритма.
Начальное состояние обрабатываемого
массива.
Сложность реализации алгоритма.
Требуемый объем памяти.
39