Похожие презентации:
Определение алгоритма. Основы алгоритмизации и программирования
1. Определение алгоритма
Основы алгоритмизациии программирования
2.
Возникновение понятияалгоритм
Слово «алгоритм» происходит от имени
выдающегося
средневекового
математика
Востока
Мухаммеда
ибн Мусы аль-Хорезми (787 – 850)
Около 825 года он написал книгу, в которой им были
предложены приемы выполнения арифметических
вычислений с многозначными числами.
3. Возникновение понятия алгоритм
Впервой
половине
XII
века
книга
аль-Хорезми в латинском переводе проникла в Европу.
Переводчик дал ей название Algorithmi de numero
Indorum («Алгорими о счете индийском»).
Слово Algorithmi (латинское написание имени
аль-Хорезми) обрело значение способа выполнения
арифметических действий посредством арабских
цифр, то есть на бумаге, без использования абака.
Именно в таком значении оно вошло во многие
Европейские языки.
Таким образом сочинения по искусству счета
стали называть алгоритмами.
4. Развитие понятия «алгоритм»
В 1684 году Готфрид Лейбниц (1647-1716) всочинении «Nova Methodvs pro maximis et minimis,
itemque tangentibus…» впервые использовал слово
«алгоритм»(Algorithmo) в еще более широком
смысле: как систематический способ решения проблем
дифференциального исчисления.
5. Развитие понятия «алгоритм»
Пользовался словом «алгоритм» и еще одинвыдающийся математик – Леонард Эйлер (1707–
1783), одна из работ которого так и называется –
«Использование нового алгоритма для решения
проблемы Пелля».
Здесь
видно,
что
Эйлер
уже
понимает
алгоритм в еще более широком смысле, а именно:
как синоним способа решения задачи.
6. Развитие понятия «алгоритм»
Вгоды
30-е
направление
XX
века
«Теория
исследования
возникает
научное
алгоритмов»
предметом
стала
разработка
которого
универсальной алгоритмической модели. Наибольший
вклад
в
теорию
алгоритмов
внесли
английский
математик
Алан
Тьюринг
русский
математик
Андрей Марков.
и
7. Развитие понятия «алгоритм»
Алан Тьюринг в 1935-1936 годах создаеттеорию
«логических
вычисляющих
машин».
Разработанная им «машина Тьюринга» стала
обязательной частью обучения будущих математиков
и компьютерщиков.
На одной из лондонских гостиниц мемориальная
доска гласит:
«Здесь родился Алан Тьюринг (1912-1954),
взломщик кодов и пионер информатики».
8. Развитие понятия «алгоритм»
АндрейМарков
в
1947
ввел
понятие
«нормального алгоритма» и впервые систематически и
строго построил общую теорию алгоритмов.
Языки
символьной
обработки
информации
(Пролог) берут свое начало от нормальных алгоритмов
Маркова.
9. Некоторые определения алгоритма
Единого«истинного»
определения
понятия
«алгоритм» не существует. Вот лишь некоторые из
предлагаемых определений:
«Алгоритм – это всякая системы вычислений,
выполняемых по строго определенным правилам, которая
после какого-либо числа шагов заведомо приводит к
решению поставленной задачи» (А. Колмогоров)
«Алгоритм – это точное предписание, определяющее
вычислительный процесс, идущий от варьируемых
исходных данных к искомому результату» (А. Марков)
10. Свойства алгоритма
11. Основными свойствами алгоритма являются:
дискретность(прерывность,
раздельность)алгоритм должен представлять процесс решения
задачи как последовательное выполнение простых
шагов
определенность - каждое правило алгоритма должно
быть четким, однозначным и не оставлять места для
произвола;
12. Основными свойствами алгоритма являются:
массовостьалгоритм
решения
задачи
разрабатывается в общем виде, то есть, он должен
быть применим для некоторого класса задач,
различающихся только исходными данными;
результативность
(конечность) – алгоритм
должен приводить к решению задачи за конечное
число шагов.
13. Способы записи алгоритмов
словесный,формульно-словесный,
графический,
язык операторных схем,
алгоритмический язык.
14. Графический (блок-схемный) способ записи алгоритмов
Что такое блок-схема?Блок-схемой
называется
графическое
изображение логической структуры алгоритма, в
котором каждый этап процесса обработки
информации
представляется
в
виде
геометрических символов (блоков), имеющих
определенную конфигурацию в зависимости от
характера выполняемых операций.
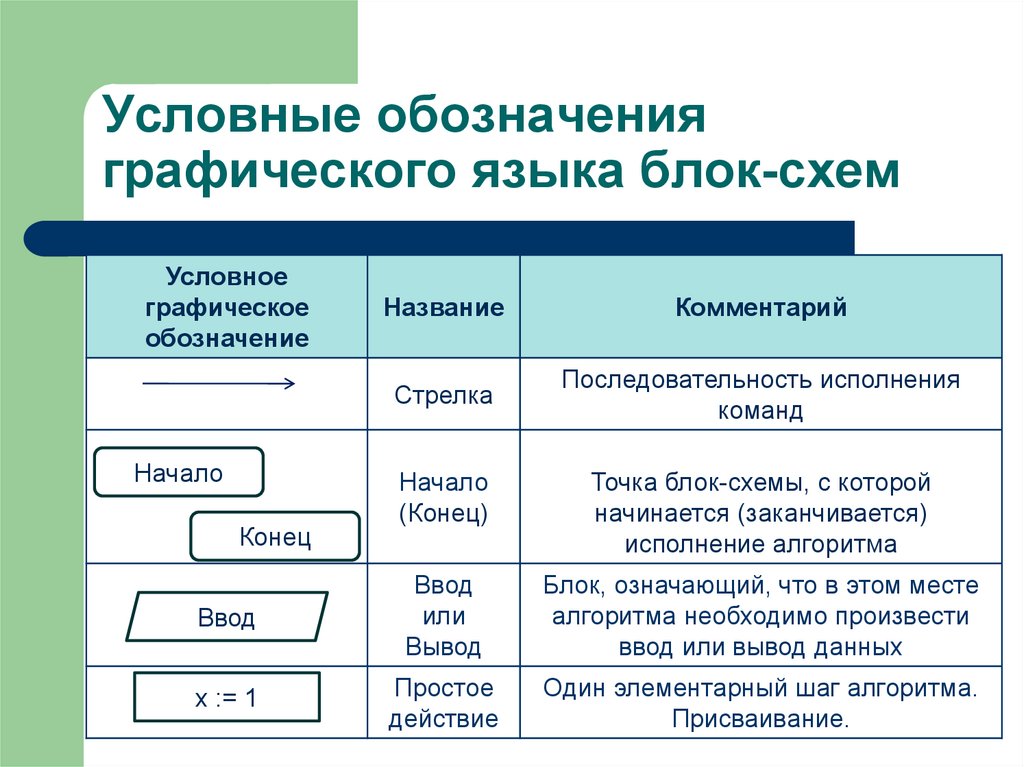
15. Условные обозначения графического языка блок-схем
Условноеграфическое
обозначение
Начало
Название
Комментарий
Стрелка
Последовательность исполнения
команд
Начало
(Конец)
Точка блок-схемы, с которой
начинается (заканчивается)
исполнение алгоритма
Ввод
Ввод
или
Вывод
Блок, означающий, что в этом месте
алгоритма необходимо произвести
ввод или вывод данных
х := 1
Простое
действие
Один элементарный шаг алгоритма.
Присваивание.
Конец
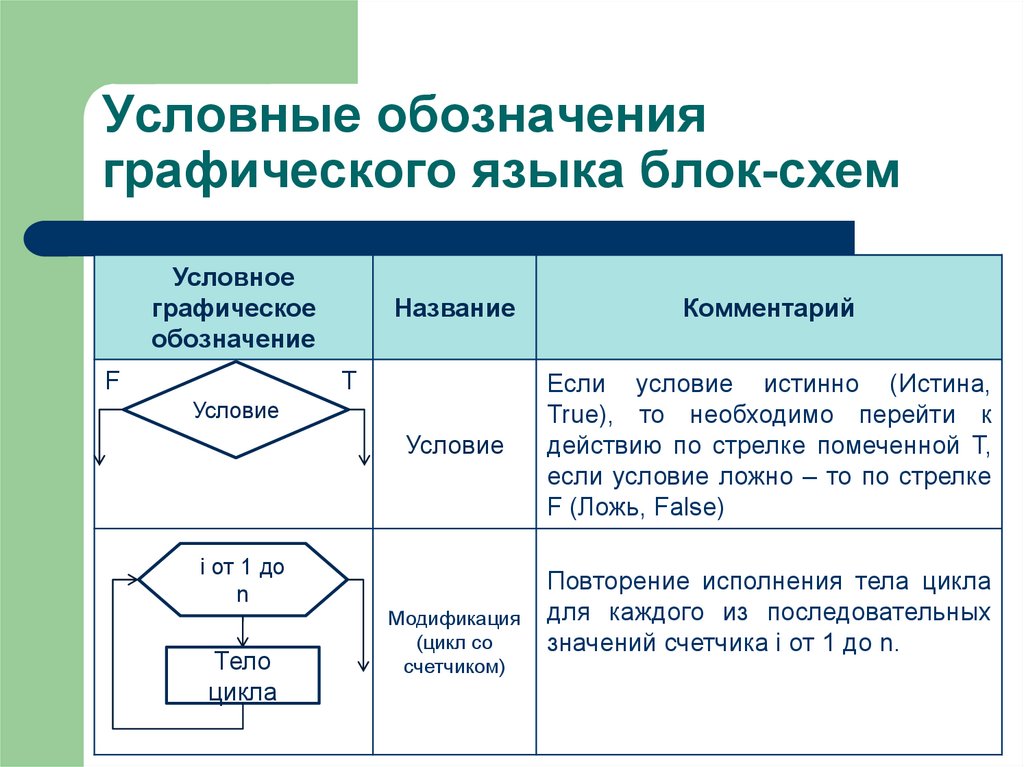
16. Условные обозначения графического языка блок-схем
Условноеграфическое
обозначение
Название
Комментарий
Условие
Если условие истинно (Истина,
True), то необходимо перейти к
действию по стрелке помеченной T,
если условие ложно – то по стрелке
F (Ложь, False)
Т
F
Условие
i от 1 до
n
Тело
цикла
Модификация
(цикл со
счетчиком)
Повторение исполнения тела цикла
для каждого из последовательных
значений счетчика i от 1 до n.
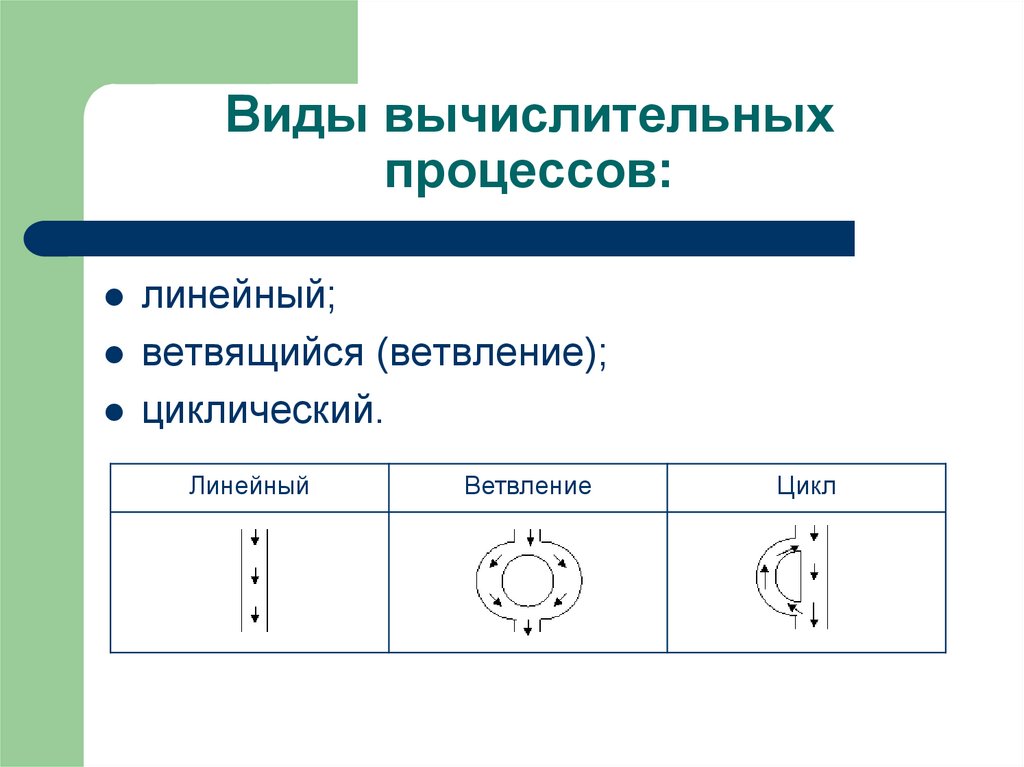
17. Виды вычислительных процессов:
линейный;ветвящийся (ветвление);
циклический.
Линейный
Ветвление
Цикл
18. Линейный алгоритм
Линейнымназывается такой
вычислительный процесс, при
котором все этапы решения
задачи
выполняются
в
естественном
порядке
следования записи этих этапов.
19. Ветвление
Разветвляющийся алгоритм содержащий хотя бы одноусловие, в результате проверки
которого происходит переход на
один из двух возможных шагов.
20. Циклические
Циклический алгоритм – алгоритм,предусматривающий
многократное
повторение одного и того же действия
(одних и тех же операций) над новыми
исходными данными.
К циклическим алгоритмам сводится
большинство методов вычислений,
перебора вариантов.
21. Пример 1. Линейный алгоритм
Составить блок-схему алгоритма, решающегоследующую задачу: даны три вещественных
положительных числа a, b и c. Найти
площадь треугольника, стороны которого
равны a, b и c.
22. Требования, предъявляемые к алгоритму. Правило 1.
При построении алгоритма необходимо задатьмножество объектов, с которыми будет работать
алгоритм.
Алгоритм приступает к работе с некоторым
набором
данных,
которые
называются
входными, и в результате своей работы выдает
данные, которые называются выходными. Таким
образом, алгоритм преобразует входные данные в
выходные.
Пока мы не имеем формализованных входных
данных, мы не можем построить алгоритм.
23. Правило 2
Для работы алгоритма требуется память.В памяти размещаются входные данные, с
которыми
алгоритм
начинает
работать,
промежуточные и выходные данные, которые
являются результатом работы алгоритма.
Память является дискретной, т.е. состоящей из
отдельных ячеек. Поименованная ячейка памяти
носит название переменной.
24. Правило 3
Дискретность.Алгоритм строится из отдельных шагов
(действий, операций, команд). Множество
шагов, из которых составлен алгоритм,
конечно.
25. Правило 5. Сходимость (результативность).
Правило 4. Детерминированность.После каждого шага необходимо указывать,
какой шаг выполняется следующим, либо давать
команду остановки.
Правило 5. Сходимость
(результативность).
Алгоритм должен завершать работу после
конечного числа шагов. При этом необходимо
указать, что считать результатом работы
алгоритма.
26. Пример 2. Алгоритмы с ветвлением
Пример2.
ветвлением
Алгоритмы
с
Составить блок-схему решения следующей
задачи: даны значения двух действительных
переменных a и b. Найти наибольшее значение
из a и b.
27. Пример 3.
Составить блок-схему решения следующейзадачи.
Даны значения действительных
переменных b и c. Решить линейное
уравнение bx+c=0.
28. Решение задач
4.5.
6.
7.
Составить блок-схему решения следующей задачи:
Даны значения действительных переменных a, b и
c, причем a≠0. Решить уравнение ax2+bx+c=0.
Дана длина ребра куба. Составьте блок схему
алгоритма нахождения площади грани, площади
полной поверхности и объема этого куба.
Составьте блок-схему вычисления периметра и
площади прямоугольного треугольника по длинам
его двух катетов.
Дана квадратная рамка. Длина внешнего края рамки
а см, длина внутреннего – b см. Составить блоксхему поиска площади рамки.

























 Программирование
Программирование








