Коллоидная химия. Адсорбция. Основные понятия (лекция 5)

1. Коллоидная химия ИТХТ им. М.В. Ломоносова кафедра НС и ПЯ группы ХХБО-01-03-2022, ХТБО-01-22

ЛЕКЦИЯ 5
Шубенкова Екатерина Гаррьевна

2. Коллоидная химия

ЛЕКЦИЯ 5
АДСОРБЦИЯ. ОСНОВНЫЕ ПОНЯТИЯ.
АДСОРБЦИЯ НА ГРАНИЦЕ ТВЕРДОЕ ТЕЛО - ГАЗ.
Шубенкова Е.Г.
2024

3. План лекции:

1. Понятие об адсорбции. Причины адсорбции.
Количественные характеристики адсорбции.
2. Адсорбция как обратимый экзотермический процесс.
Интегральная и дифференциальная теплота адсорбции.
Изобара адсорбции.
3. Сравнительная характеристика физической адсорбции
и хемосорбции. Природа адсорбционных сил. Уравнение
Леннард – Джонса.
4. Теория мономолекулярной адсорбции Ленгмюра. Вывод
и анализ уравнения изотермы мономолекулярной
адсорбции Ленгмюра.
5. Линейная форма уравнения Ленгмюра. Нахождение
констант уравнения Ленгмюра графическим методом.
Определение удельной поверхности адсорбента.
6. Полимолекулярная теория адсорбции Поляни.
7. Теория полимолекулярной адсорбции БЭТ. Уравнение
БЭТ, его решение графическим методом.

4. Основные определения

5. Адсорбция как обратимый экзотермический процесс

В адсорбционном слое молекулы газа способны к
перемещению лишь в двух измерениях, поэтому
адсорбция газа сопровождается уменьшением
энтропии, т.е. ΔS < 0
Условием протекания адсорбции как
самопроизвольного процесса является уменьшение
энергии Гиббса, т. е. ΔG < 0
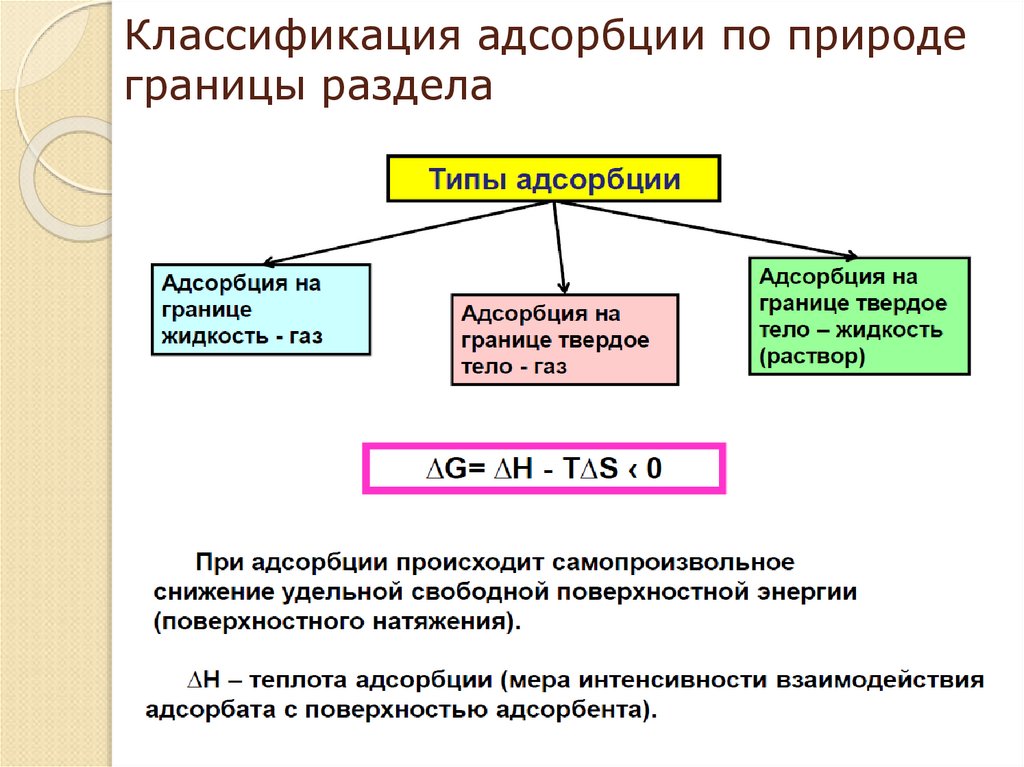
Таким образом из термодинамической зависимости
ΔG = ΔH −T ⋅ΔS
следует, что теплота адсорбции должна быть
отрицательной, т. е. адсорбция газов или паров на
твердом теле всегда является экзотермическим
процессом.

6. Интегральная и дифференциальная теплота адсорбции

Различают дифференциальную и интегральную
теплоту адсорбции.
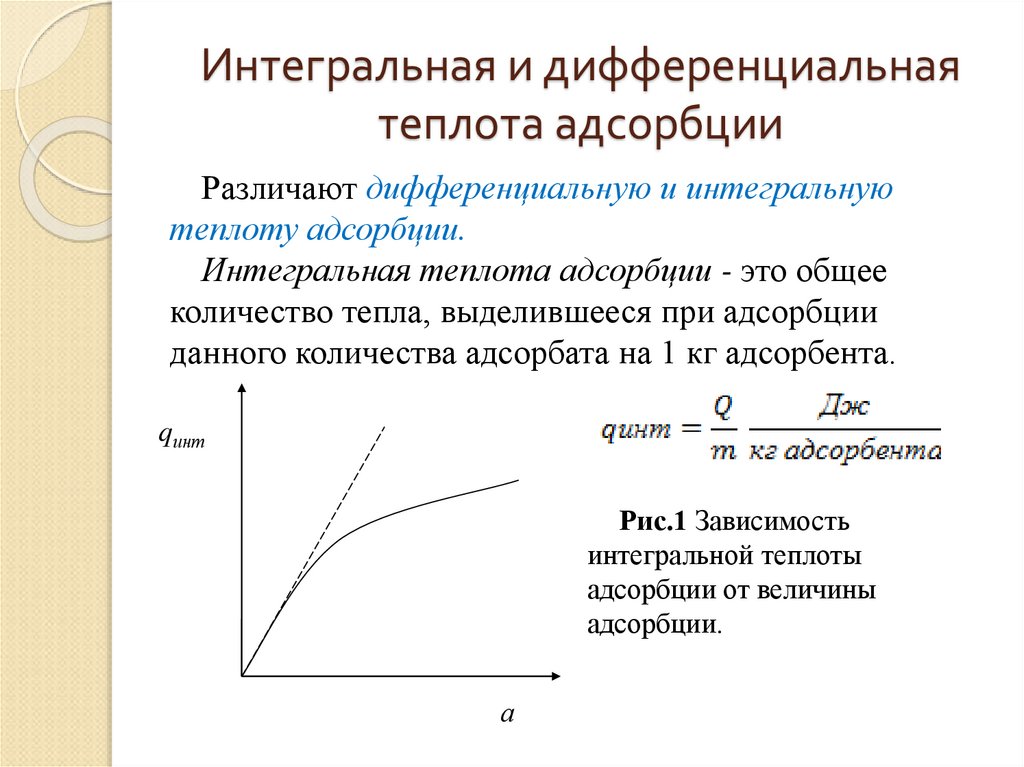
Интегральная теплота адсорбции - это общее
количество тепла, выделившееся при адсорбции
данного количества адсорбата на 1 кг адсорбента.
qинт
Рис.1 Зависимость
интегральной теплоты
адсорбции от величины
адсорбции.
а

7. Дифференциальная теплота адсорбции

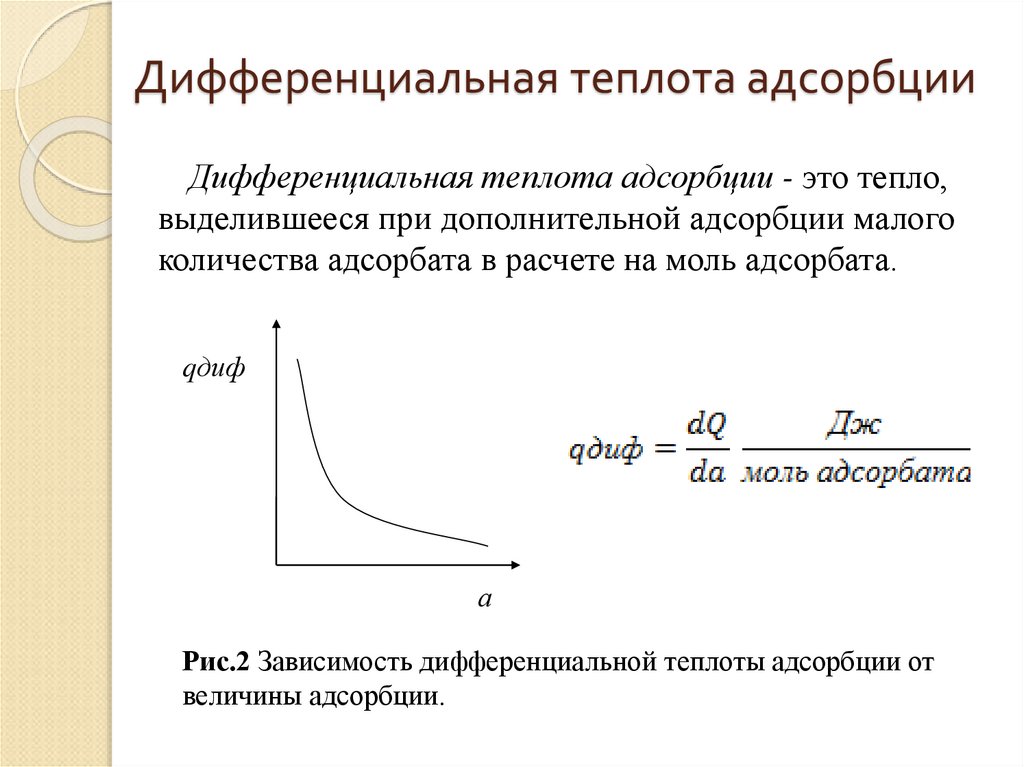
Дифференциальная теплота адсорбции - это тепло,
выделившееся при дополнительной адсорбции малого
количества адсорбата в расчете на моль адсорбата.
qдиф
а
Рис.2 Зависимость дифференциальной теплоты адсорбции от
величины адсорбции.

8. Обратимость адсорбции

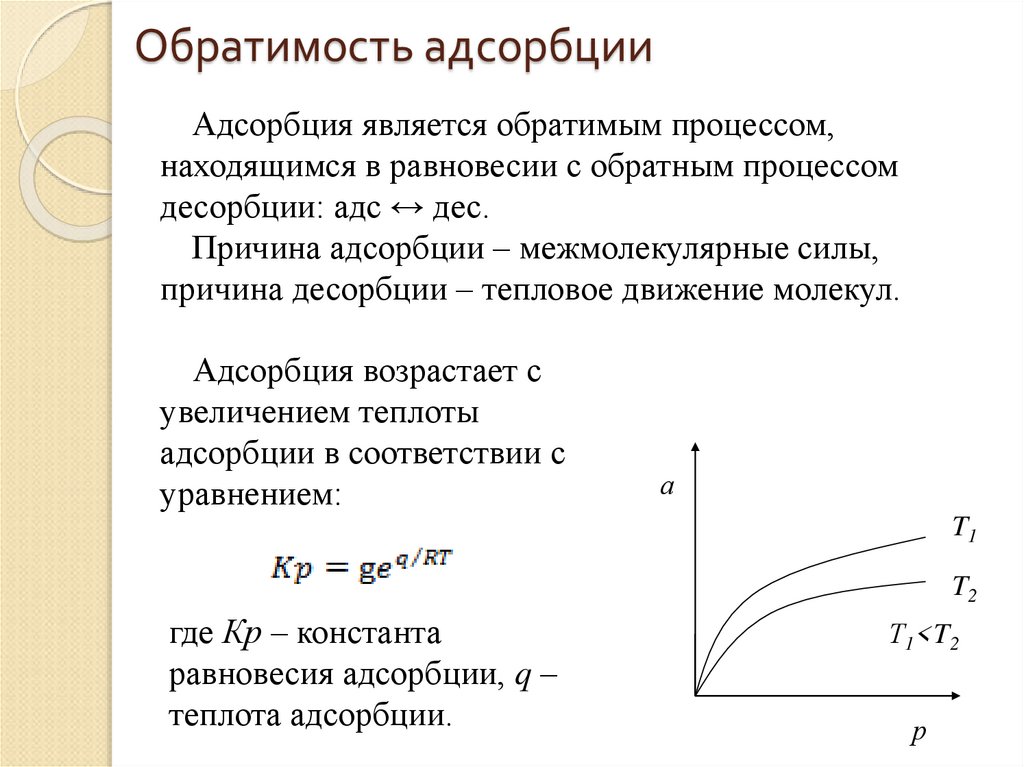
Адсорбция является обратимым процессом,
находящимся в равновесии с обратным процессом
десорбции: адс ↔ дес.
Причина адсорбции – межмолекулярные силы,
причина десорбции – тепловое движение молекул.
Адсорбция возрастает с
увеличением теплоты
адсорбции в соответствии с
уравнением:
а
T1
T2
где Кр – константа
равновесия адсорбции, q –
теплота адсорбции.
Т1<T2
р

9. Количественные характеристики адсорбции

10. Типы адсорбционных зависимостей

Основным законом, определяющим
поведение компонентов при адсорбции,
является закон распределения НернстаШилова. Величина адсорбции компонентов
зависит от температуры и концентрации или
давления.
A = f [T, C(или p)]
Различают следующие виды адсорбционных
зависимостей:
A = f (C) или A = f ( p) при T = const изотерма адсорбции;
A = f (T) при p = const – изобара адсобции ;
P = f (T) или C = f (T) при А = const изостера адсорбции.

11. Основные экспериментальные зависимости адсорбции

A f ( p)
T2 T1
A f (T )
p f (T )
Основные
экспериментальные
зависимости адсорбции
1. Изотерма адсорбции - зависимость
адсорбции
от
равновесного
давления
(концентрации) при Т=const.
2. Изобара (изопикна) адсорбции зависимость адсорбции от температуры при р,С =
const.
где: 1 – изобара при физической
адсорбции,
2 – изобара при хемосорбции.
3. Изостера адсорбции - зависимость
давления от температуры при А=const.

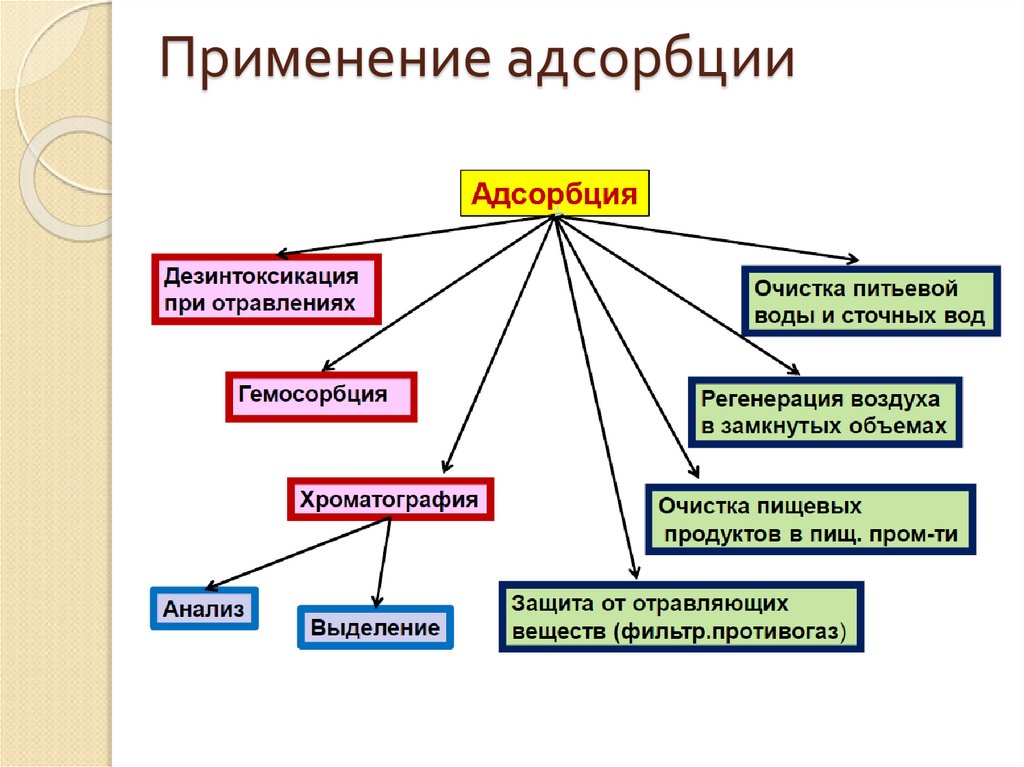
12. Применение адсорбции

13. Классификация адсорбции по природе границы раздела

14.

15. Адсорбция газов и паров на твердой поверхности

Это простейший случай адсорбции, т.к.
адсорбционном процессе участвуют только два
компонента.
Степень адсорбции в состоянии равновесия
зависит от температуры, давления газа и
удельной поверхности адсорбента.
A = f [T, Р, Sуд]
Лучшими адсорбентами являются
высокопористые вещества, у таких
адсорбентов как активированный уголь и
силикагель Sуд достигает 1000 м2/г.

16. Адсорбция на твердой поверхности

По типу взаимодействия адсорбата и адсорбента
различают физическую адсорбцию, хемосорбцию и
ионный обмен.
Хемосорбция химического соединения.
процесс
образования
поверхностного

17. Физическая и химическая адсорбция

Физическая адсорбция
Хемосорбция
Обусловлена физическими силами
(силами Ван-дер-Ваальса)
Обусловлена химическими силами
Теплота адсорбции мала, 10-40
кДж/моль
Теплота адсорбции велика, 40-400
кДж/моль
С повышением температуры часто
уменьшается (преобладает процесс
десорбции)
Повышение температуры
способствует процессу адсорбции
(достигается Еа)
Мало специфична, слабо зависит от
природы адсорбата
Специфична, часто образуется
поверхностное химическое
соединение
Обратима (что адсорбируется, то и
десорбируется)
Часто необратима
Не локализованная (молекулы
адсорбата способны перемещаться по
поверхности адсорбента)
Локализованная (молекулы адсорбата
связаны с адсорбентом за счет
прочных химических связей)

18.

6. Адсорбционное равновесие
достигается быстро, физическая
адсорбция многослойна.
6. Монослойна. Хемосорбция
отличается от химической р-ции
тем, что адсорбция протекает
только в мономолекулярном
поверхностном слое и не идет
вглубь диффузия адсорбата.
Хемосорбция О2 на угле.
Образуется адсорбционный
компонент который препятствует
проникновению О вглубь:

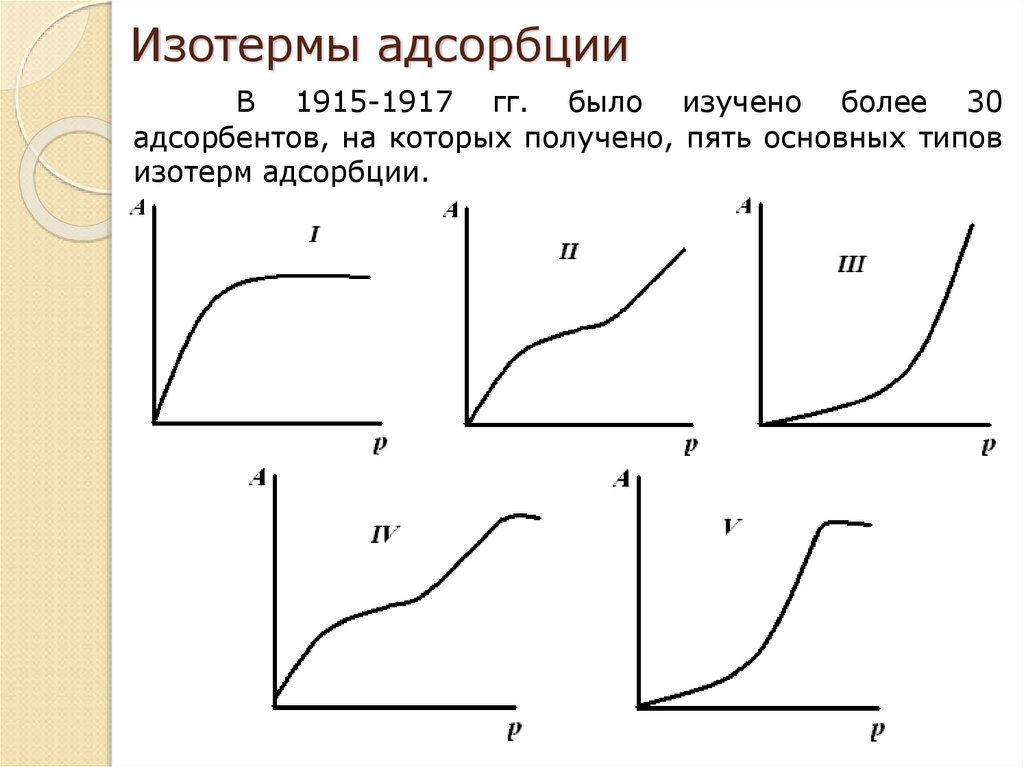
19. Изотермы адсорбции

В 1915-1917 гг. было изучено более 30
адсорбентов, на которых получено, пять основных типов
изотерм адсорбции.

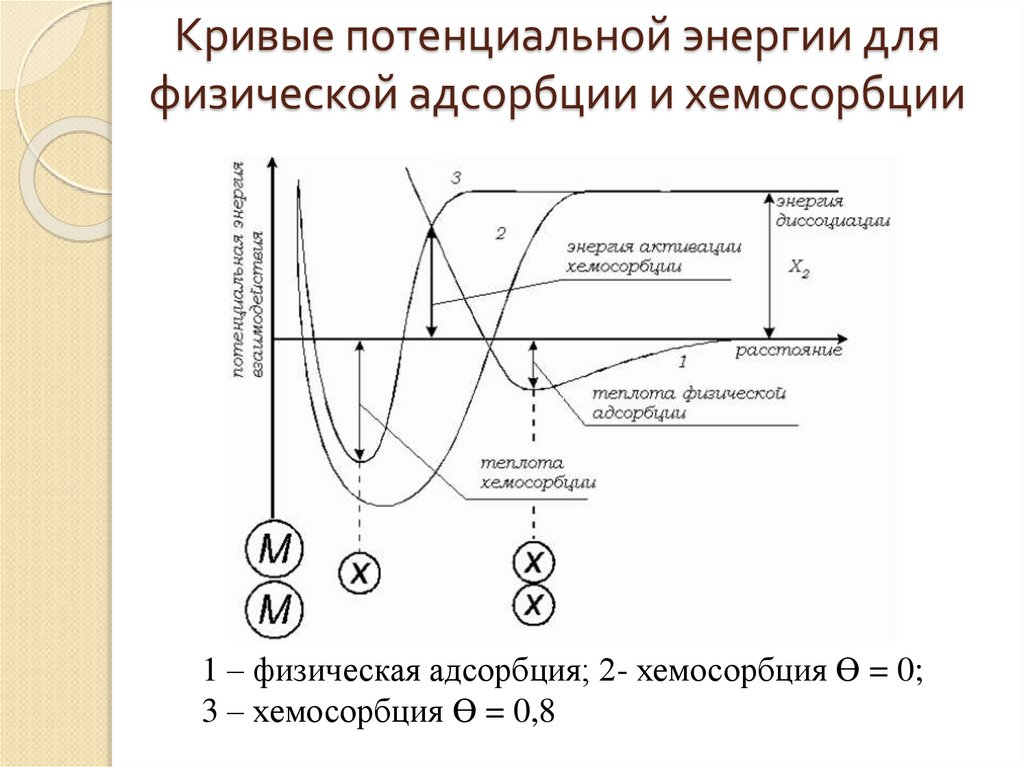
20. Кривые потенциальной энергии для физической адсорбции и хемосорбции

1 – физическая адсорбция; 2- хемосорбция ϴ = 0;
3 – хемосорбция ϴ = 0,8

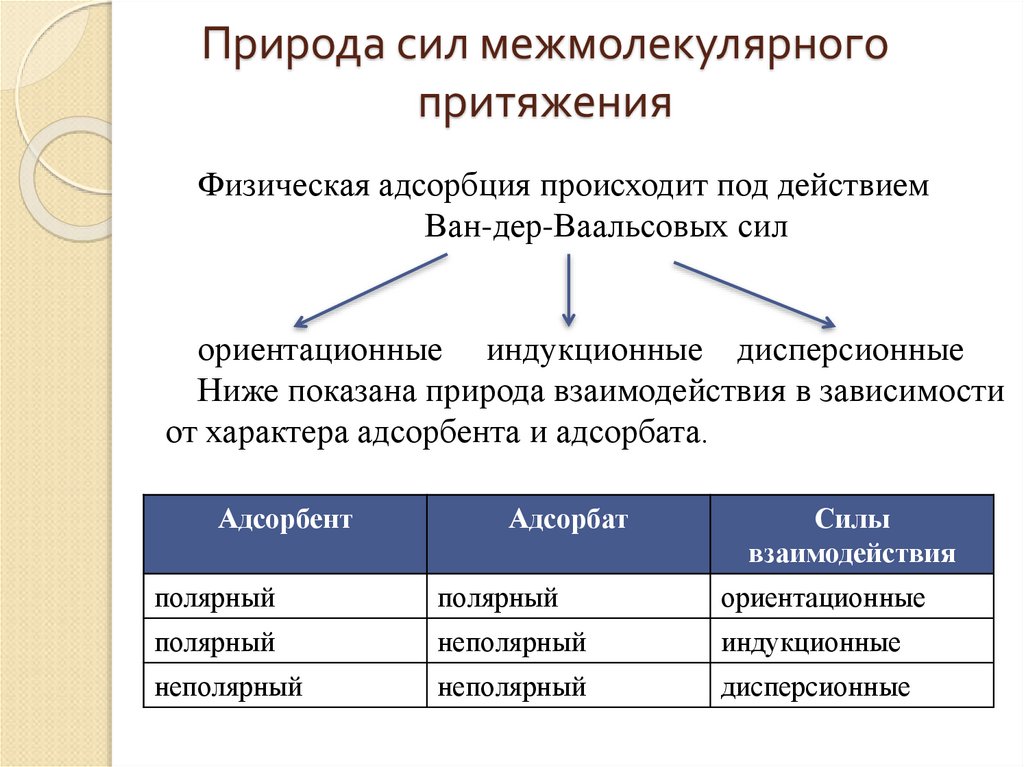
21. Природа сил межмолекулярного притяжения

Физическая адсорбция происходит под действием
Ван-дер-Ваальсовых сил
ориентационные индукционные дисперсионные
Ниже показана природа взаимодействия в зависимости
от характера адсорбента и адсорбата.
Адсорбент
Адсорбат
Силы
взаимодействия
полярный
полярный
ориентационные
полярный
неполярный
индукционные
неполярный
неполярный
дисперсионные

22.

Дисперсионные силы имеют квантовую природу,
проявляются между мгновенными диполями,
возникающими при сближении молекул за счет
флуктуаций электронной плотности.
Энергия межмолекулярного взаимодействия:
Uмежмол. взаим. = Uинд. + Uор. + Uдисп.
Для сильно поляризованных молекул NH3 и H2O
ориентационный эффект = дисперсионному.
Адсорбционные силы действуют на больших
расстояниях по сравнению с межмолекулярными
силами rад ~10-7 м; rмежмол ~10-9 м.

23.

Уравнение Леннард-Джонса
Энергия межмолекулярного (дисперсионного)
притяжения:
где С – константа дисперсионного притяжения, зависит
от природы сил; r – расстояние между центрами атомов
и молекул.
Энергия борновского отталкивания:
где b - константа борновского отталкивания,
происходящего при перекрывании электронных орбит.
Полная энергия адсорбционного взаимодействия
определяется уравнением Леннард-Джонса:
При адсорбции дисперсионные силы действуют
одновременно между молекулами адсорбата и многими
атомами адсорбента.
Полная потенциальная энергия взаимодействия:

24. Теории адсорбции

25. Теория Ленгмюра

1)
Адсорбция является локализованной и
вызывается силами, близкими к химическим.
2)
Адсорбция происходит не на всей
поверхности адсорбента, а на активных
центрах, которыми являются выступы либо
впадины
на
поверхности
адсорбента,
характеризующиеся наличием т.н. свободных
валентностей. Активные центры считаются
независимыми (т.е. один активный центр не
влияет на адсорбционную способность других),
и тождественными.
3)
Каждый активный центр способен взаимодействовать
только с одной молекулой адсорбата; в результате на
поверхности
может
образоваться
только
один
слой
адсорбированных молекул.
4) Процесс адсорбции является обратимым и равновесным –
адсорбированная молекула удерживается активным центром
некоторое время, после чего десорбируется; т.о., через
некоторое время между процессами адсорбции и десорбции
устанавливается динамическое равновесие.

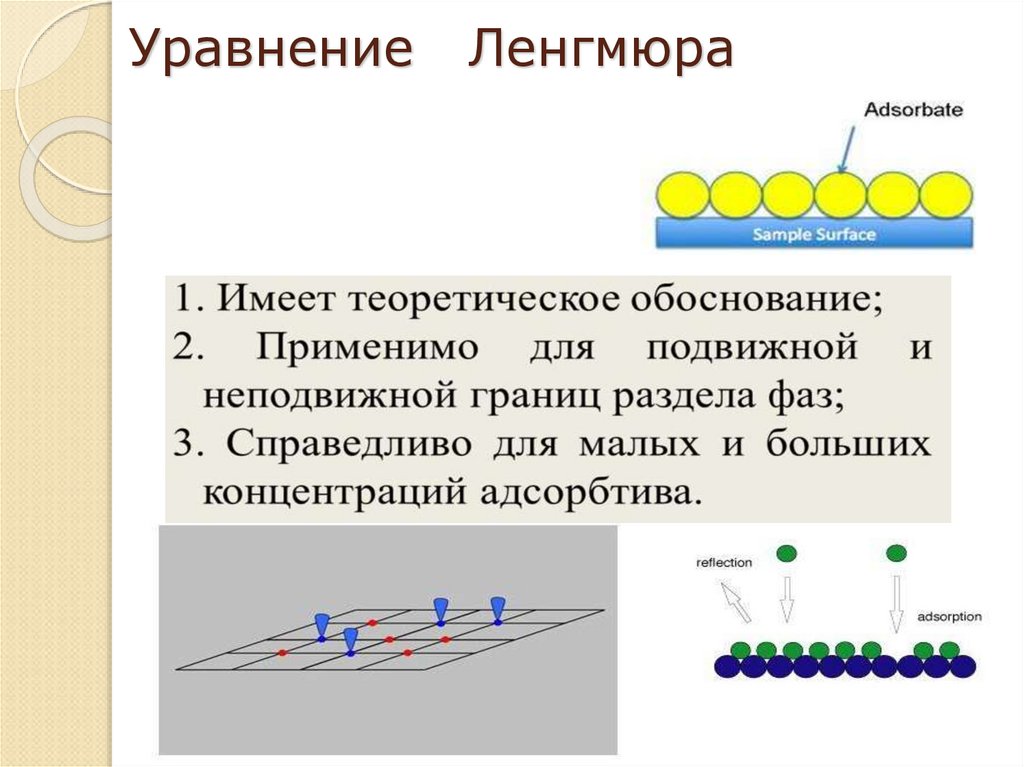
26. Уравнение Ленгмюра

27.

мол-ла газа + акт. центр ↔ адсорбционный комплекс
р
А0
А
р – давление газа; А0 – концентрация свободных
активных центров; А – концентрация занятых активных
центров. Тогда константа равновесия:
Аmax = A + А0
А0 = Аmax − A
Аmax – максимальная адсорбция при
образовании мономолекулярного слоя.
К р(Аmax − A) = А
КрАmax − КрA =А
1уч – А = КрАmax
2 уч −
3 уч – А = Аmax

28. Уравнение адсорбции Лэнгмюра (1915 г.)

Кр
А А
1 Кр
КС
А А
1 КС
Величина А∞ зависит:
от числа адсорбционных центров на
поверхности или массы адсорбента;
от размеров молекул адсорбата, чем
молекула, тем меньше А∞.
единице
крупнее

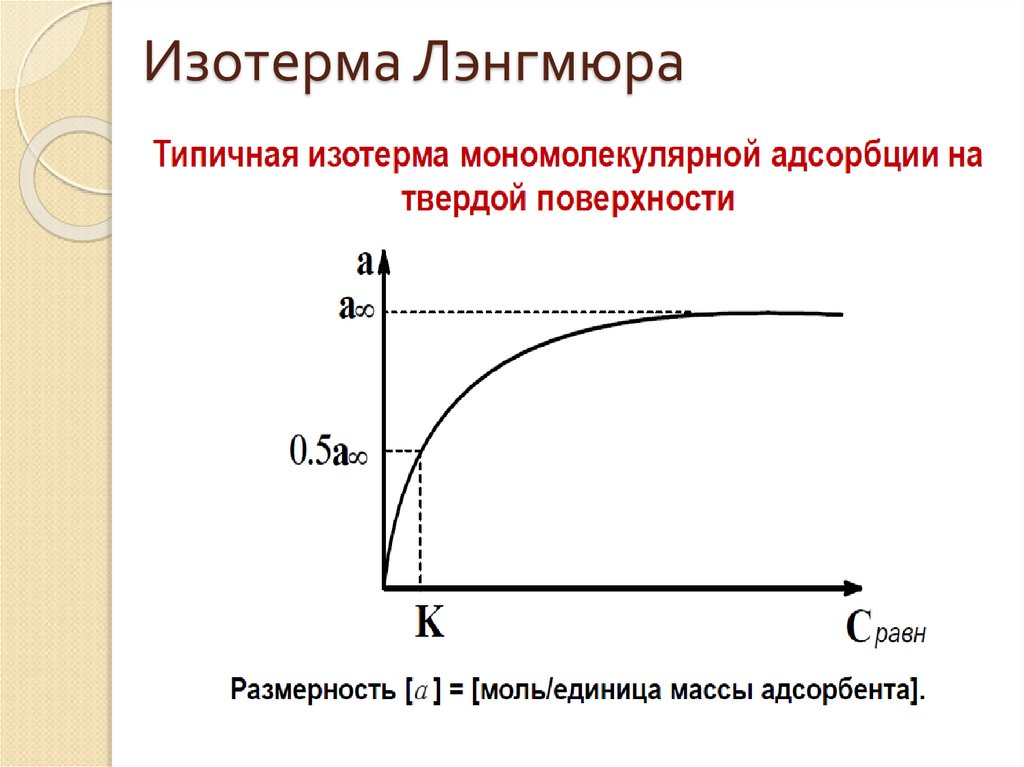
29. Изотерма Лэнгмюра

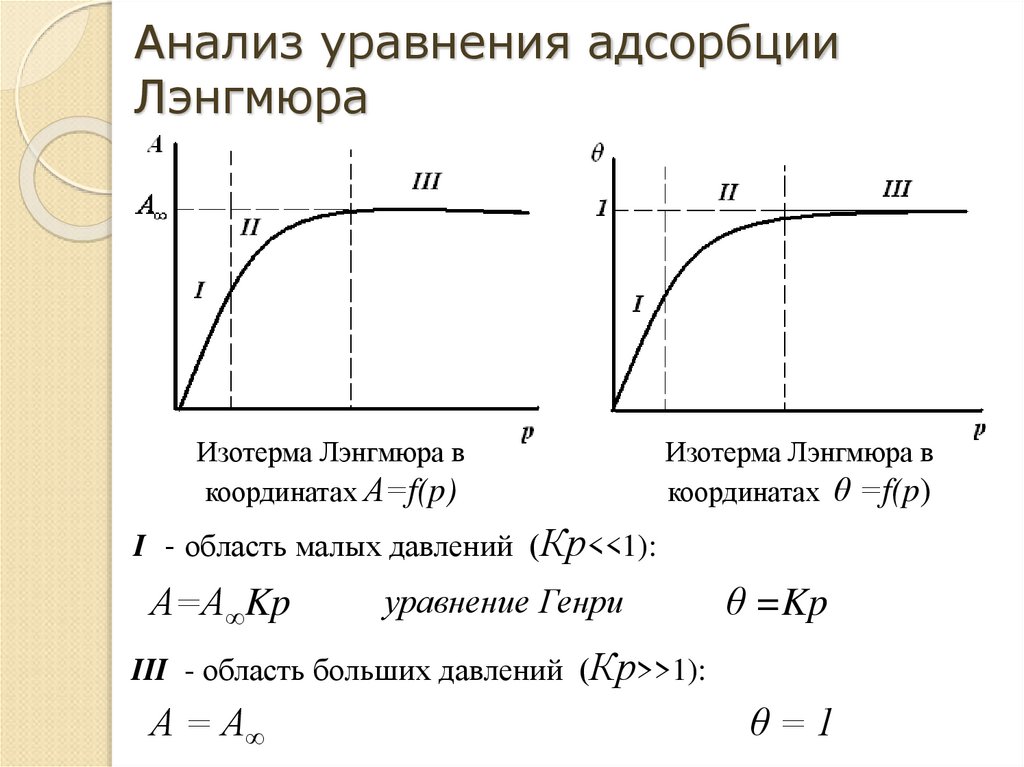
30. Анализ уравнения адсорбции Лэнгмюра

Изотерма Лэнгмюра в
координатах А=f(p)
Изотерма Лэнгмюра в
координатах θ =f(p)
I - область малых давлений (Кр<<1):
А=А∞Kp
уравнение Генри
θ =Kp
III - область больших давлений (Кр>>1):
А = А∞
θ=1

31.

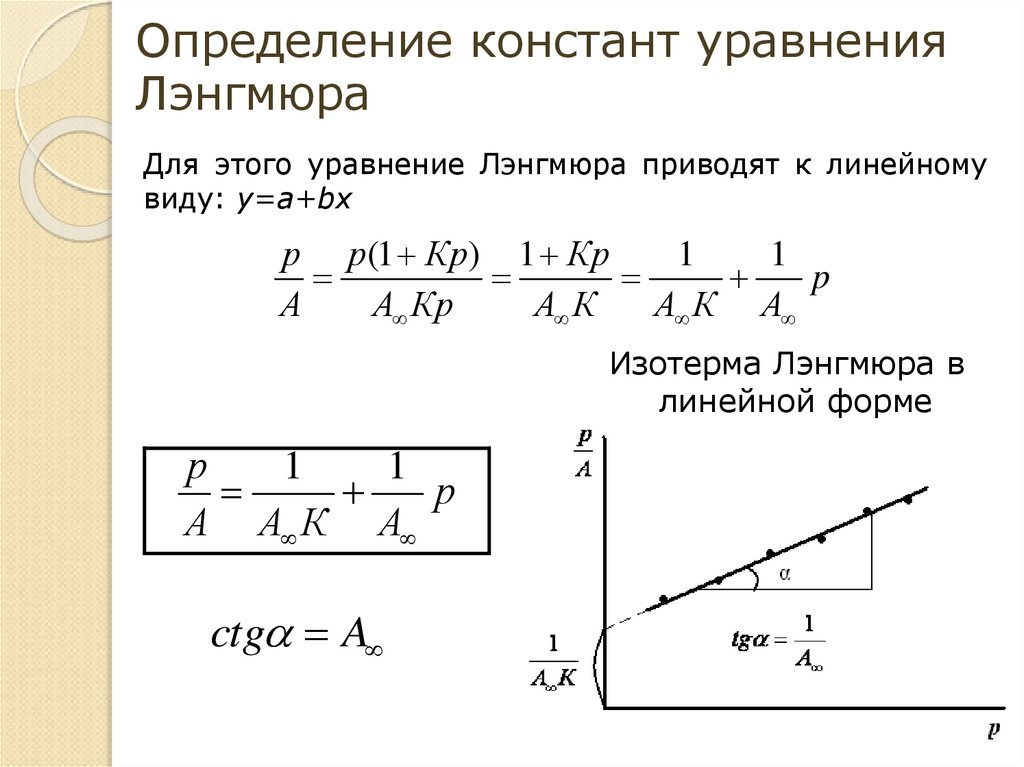
Определение констант уравнения
Лэнгмюра
Для этого уравнение Лэнгмюра приводят к линейному
виду: y=a+bx
р р(1 Кр) 1 Кр
1
1
p
А
А Кр
А К
А К А
Изотерма Лэнгмюра в
линейной форме
р
1
1
р
А А К А
ctg A

32. Экспериментальное определение величины адсорбции

33.

Эмпирическое уравнение адсорбции
Фрейндлиха
А p n
1
Физический смысл констант:
β –
значение адсорбции при парциальном
давлении газа, равном единице (при р=1, А = β),
β =2
÷ 2,5
1/n характеризует степень отклонения изотермы
адсорбции от прямой линии, 1/n = 0,2 ÷ 0,7.
Константы уравнения Фрейндлиха из опытных
данных определяют графически. Для этого уравнение
логарифмируют:
1
lg A lg lg p
n

34.

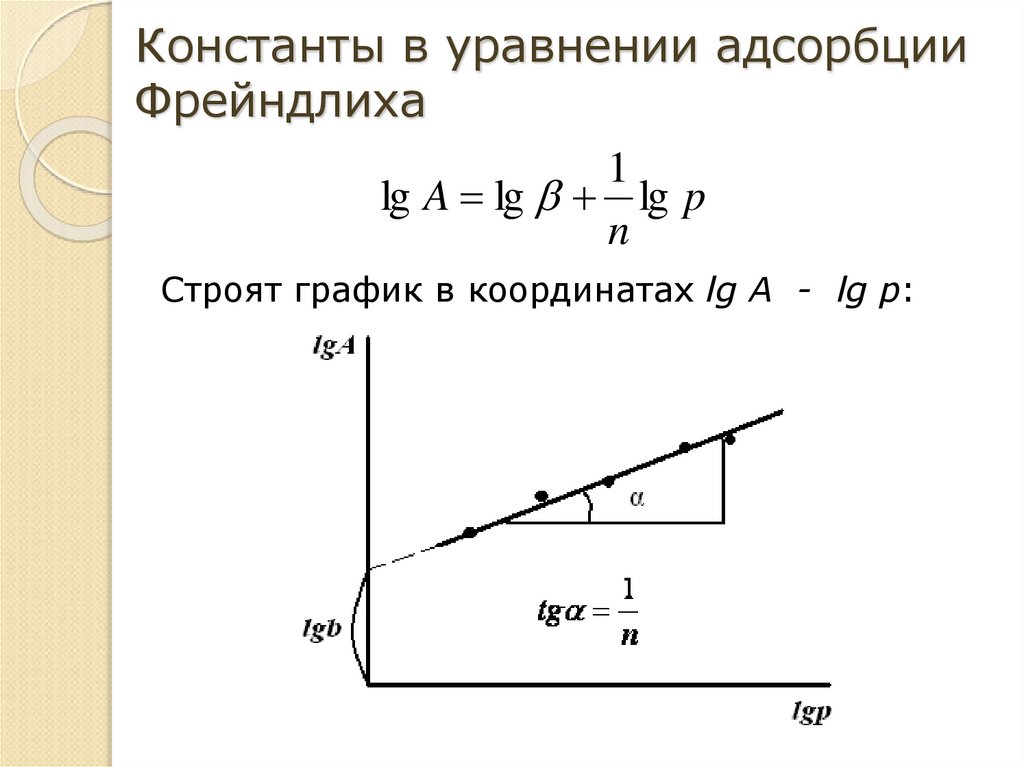
Константы в уравнении адсорбции
Фрейндлиха
1
lg A lg lg p
n
Строят график в координатах lg A - lg p:

35. Применимость уравнения Фрейндлиха

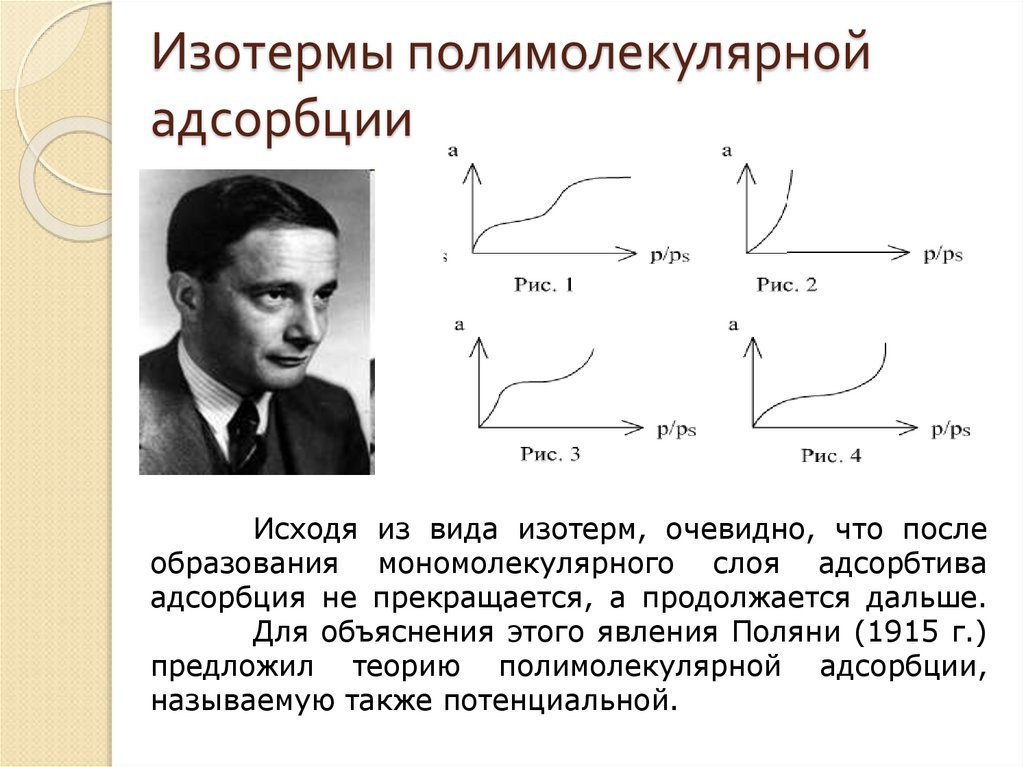
36. Изотермы полимолекулярной адсорбции

Исходя из вида изотерм, очевидно, что после
образования мономолекулярного слоя адсорбтива
адсорбция не прекращается, а продолжается дальше.
Для объяснения этого явления Поляни (1915 г.)
предложил теорию полимолекулярной адсорбции,
называемую также потенциальной.

37. Теория Поляни

38. Характеристическая кривая

(адсорбционный потенциал) – работа
адсорбции в зависимости от толщины (Х)
слоя адсорбированного вещества (величины
адсорбции Г) .

39. Теория БЭТ

Мономолекулярная теория адсорбции Лэнгмюра
и полимолекулярная Поляни - имеют как преимущества
так и недостатки. Одной из наиболее удачных попыток
обобщить эти две теории и создать на их основе единую
теорию является создание теории БЭТ (теория
Брунауэра - Эммета - Теллера, 1935-1940 гг.).

40. Положения теории БЭТ

1.
2.
3.
4.
На поверхности адсорбента имеется
определенное число активных центров,
способных удерживать молекулы адсорбтива.
Взаимодействием адсорбированных молекул в
первом и последующих слоях
пренебрегают.
Каждая молекула первого слоя может стать
активным центром для адсорбции и
образования второго и последующего слоев.
Предполагается, что во втором и последующих
слоях все молекулы имеют такую
же сумму статистических состояний, как
жидкости.

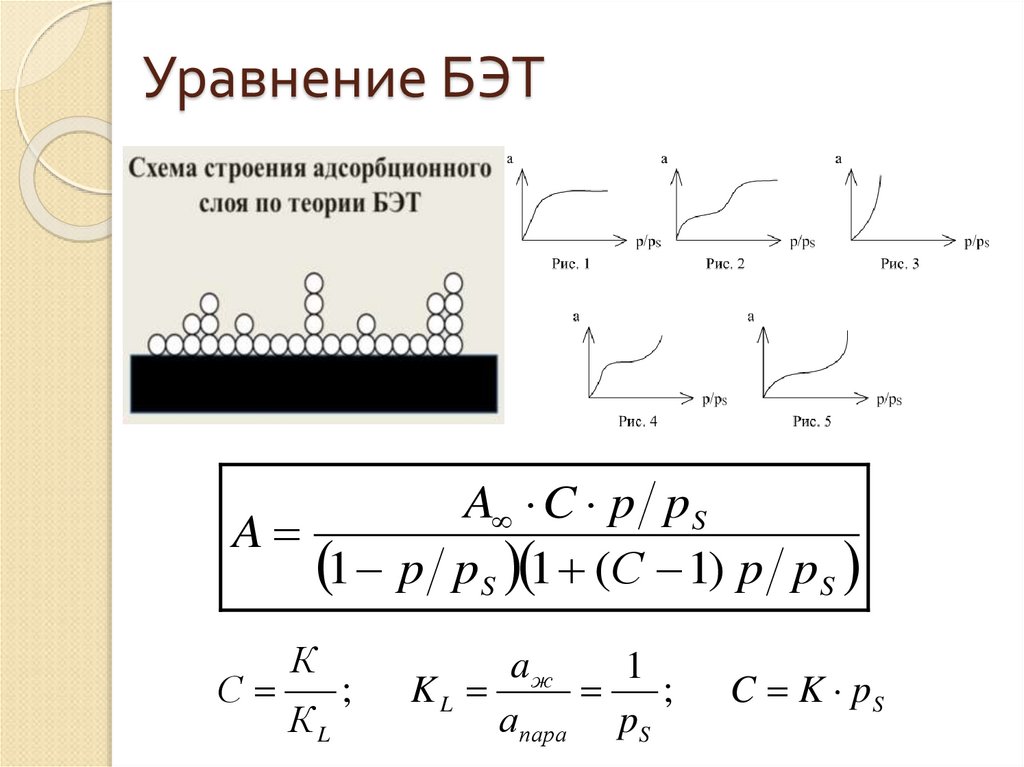
41. Уравнение БЭТ

A C p pS
A
1 p pS 1 (С 1) p pS
С
К
КL
;
aж
1
KL
;
апара pS
C K pS

42. Константы уравнения БЭТ

Строим
график
уравнения БЭТ:
линейной
p pS
1
(С 1)
p pS
А 1 p pS A С
A С
формы