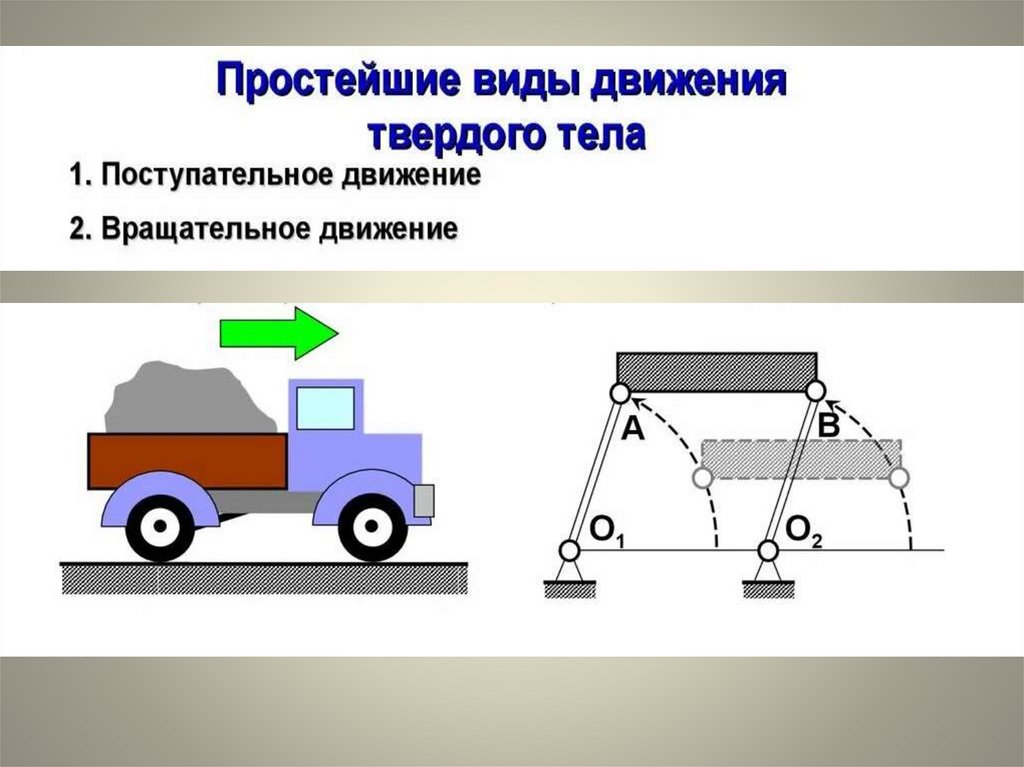
Простейшие виды движения твердого тела

1.

2.

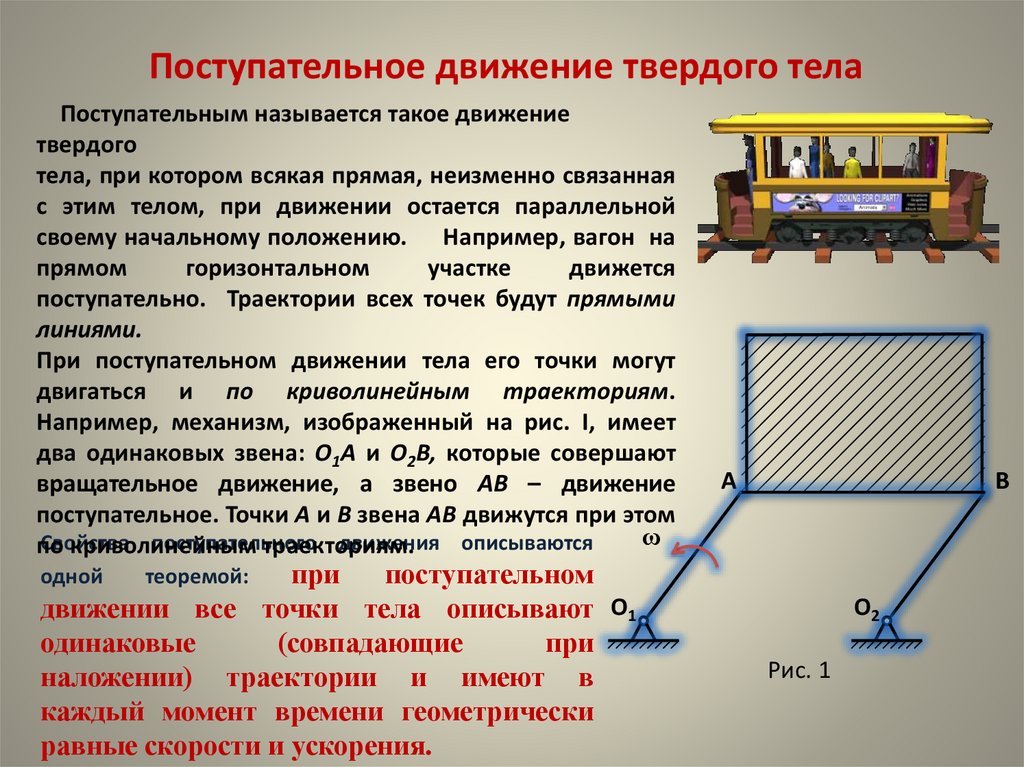
Поступательное движение твердого тела
Поступательным называется такое движение
твердого
тела, при котором всякая прямая, неизменно связанная
с этим телом, при движении остается параллельной
своему начальному положению. Например, вагон на
прямом
горизонтальном
участке
движется
поступательно. Траектории всех точек будут прямыми
линиями.
При поступательном движении тела его точки могут
двигаться и по криволинейным траекториям.
Например, механизм, изображенный на рис. I, имеет
два одинаковых звена: O1A и O2B, которые совершают
вращательное движение, а звено AB – движение
поступательное. Точки A и B звена AB движутся при этом
ω
Свойства
поступательного
движения описываются
по
криволинейным
траекториям.
при
поступательном
движении все точки тела описывают O1
одинаковые
(совпадающие
при
наложении) траектории и имеют в
каждый момент времени геометрически
равные скорости и ускорения.
одной
A
B
теоремой:
O2
Рис. 1

3.

Так как все точки тела при поступательном движении
движутся одинаково, то уравнениями поступательного
движения тела являются уравнения движения любой его
точки.
Например, для звена AB (рис.1) уравнениями движения в
координатной форме могут быть уравнения движения точки A:
Только для поступательного движения твердого
тела можно говорить о скорости и ускорении тела, так
как все точки тела движутся одинаково.

4.

Вращательным
называется
такое
движение твердого тела, при котором все его
точки, лежащие на прямой, называемой
осью вращения, остаются неподвижными.
Для тела, закрепленного в подшипнике A
и подпятнике B, прямая AB, проходящая
через эти точки, является осью вращения.
Точки тела, не лежащие на оси вращения,
движутся по окружностям. Если с телом
жестко связать подвижную плоскость Q, то
поворот этой плоскости относительно
неподвижно плоскости P определяет поворот
тела относительно оси вращения, который
изменяется с течением времени
A
P
Q
ϕ
B
Это уравнение является кинематическим уравнением вращательного
движения твердого тела.
Угол поворота тела измеряется в радианах.

5.

Угловая скорость ω характеризует изменение угла поворота тела за
единицу времени
Знак угловой скорости определяет направление вращения тела
вокруг оси. Если ω > 0, то тело вращается против хода часовой стрелки.
Размерность угловой скорости – рад/с или 1/с.
В технике скорость вращения тела определяют числом оборотов в
минуту n. При равномерном вращении тела существует следующая
зависимость между угловой скоростью ω и частотой вращения n :
Угловое ускорение ε характеризует изменение угловой
скорости тела в единицу времени

6.

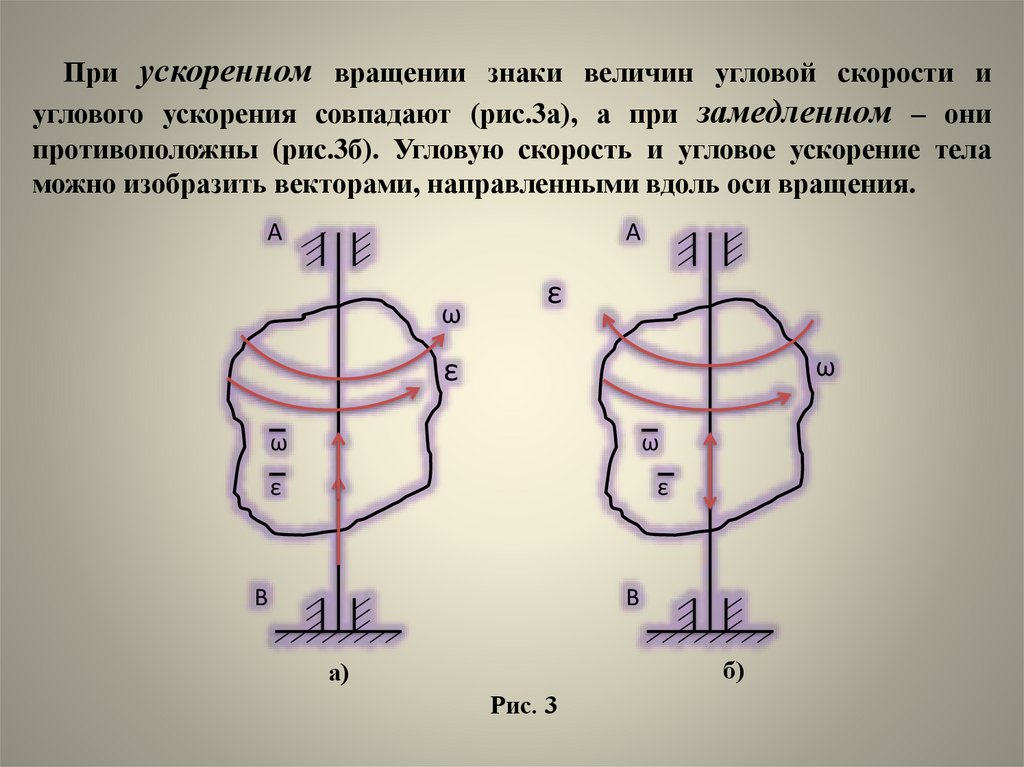
При ускоренном вращении знаки величин угловой скорости и
углового ускорения совпадают (рис.3а), а при замедленном – они
противоположны (рис.3б). Угловую скорость и угловое ускорение тела
можно изобразить векторами, направленными вдоль оси вращения.
A
A
ω
ε
ω
ε
ω
ω
ε
ε
B
B
б)
а)
Рис. 3

7.

Если угловая скорость тела остается во все время движения постоянной
ω = const, то вращение тела называется равномерным.
Уравнение равнопеременного вращения тела имеет вид
где
Vс VB
ϕ0 – начальный угол поворота тела
(при t =0);
ω0 – начальная угловая скорость;
ε – угловое ускорение тела.
Любая точка вращающегося тела, не лежащая
на оси вращения, движется по окружности в
плоскости, перпендикулярной оси вращения.
Скорость
точки
пропорциональна
расстоянию точки до оси вращения и
зависит от угловой скорости тела (рис.4).
M
VA
h
O
VM
C B
ω
Рис. 4
Скорость точки вращающегося тела называют линейной.
Вектор скорости точки направлен перпендикулярно радиусу,
соединяющему точку с осью вращения.
A

8.

Так как все точки вращающегося тела движутся по окружностям, то их
скорости изменяются как по величине, так и по направлению.
Ускорение
точки
будет
представлено
двумя
составляющими
где αn - нормальное ускорение точки, характеризует изменение
скорости по направлению; зависит от радиуса кривизны ρ
траектории, т.е. расстояния h точки до оси вращения
ατ – касательное ускорение, характеризует изменение
модуля скорости точки с течение времени; зависит от углового
ускорения ε и расстояния h точки до оси вращения

9.

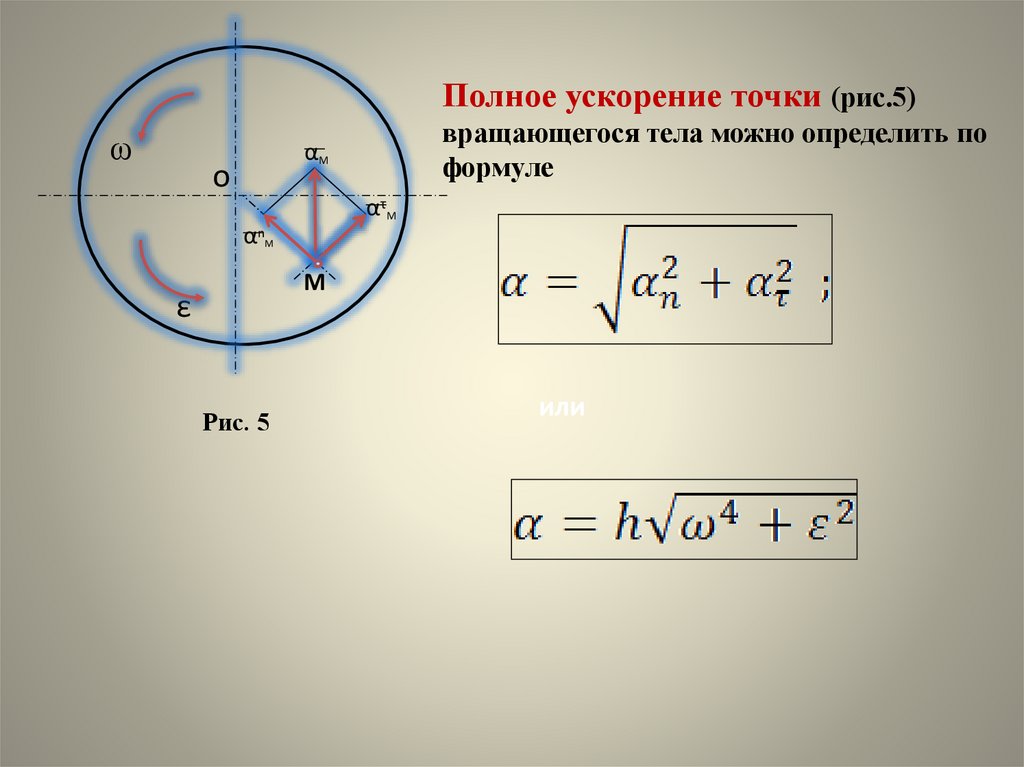
Полное ускорение точки (рис.5)
ω
вращающегося тела можно определить по
формуле
αM
o
ατM
αnM
M
ε
Рис. 5
или