Экономические индексы

1. Экономические индексы

Сущность и виды индексов
Индивидуальные и сводные
индексы
3. Индексы средних величин
4. Территориальные индексы
1.
2.

2. 1. Сущность и виды индексов

Индекс - относительная величина,
характеризующая изменение уровней
сложных
социально-экономических
показателей:
во времени,
в пространстве или
по сравнению с планом.
Индексы, по аналогии с относительными
величинами, могут быть построены как
индексы динамики, выполнения плана,
планового задания, сравнения.

3. Задачи:

характеристика общего изменения
сложного экономического
показателя и отдельных его
элементов;
измерение влияния факторов на
общую динамику сложного
показателя

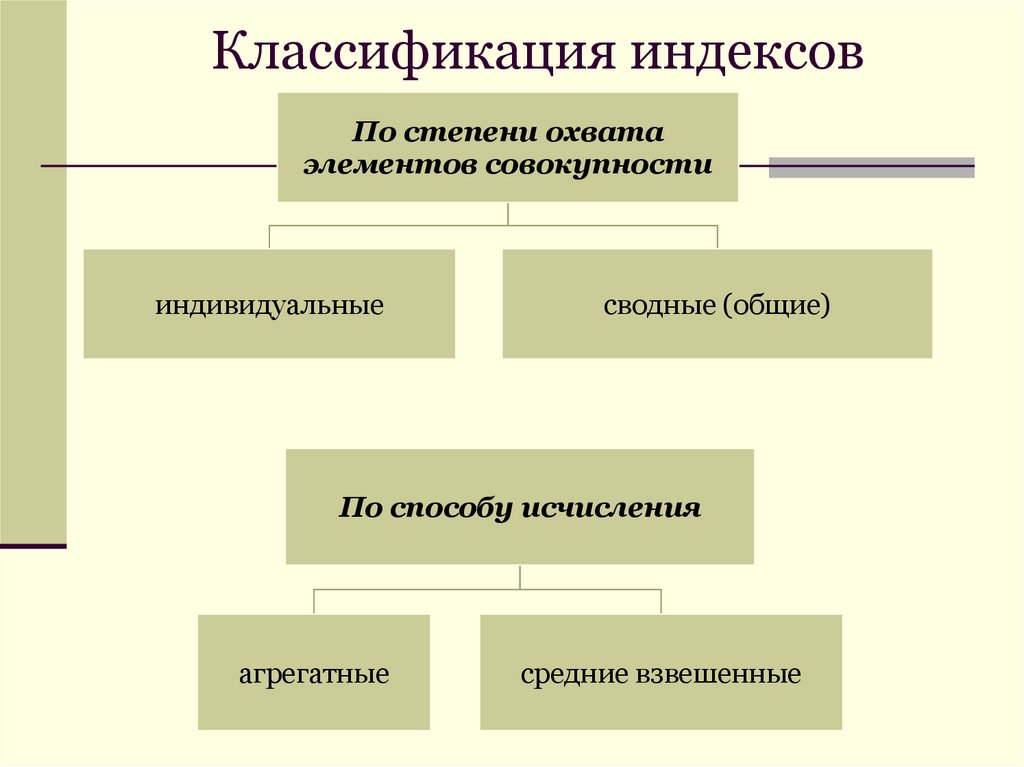
4. Классификация индексов

По степени охвата
элементов совокупности
индивидуальные
сводные (общие)
По способу исчисления
агрегатные
средние взвешенные

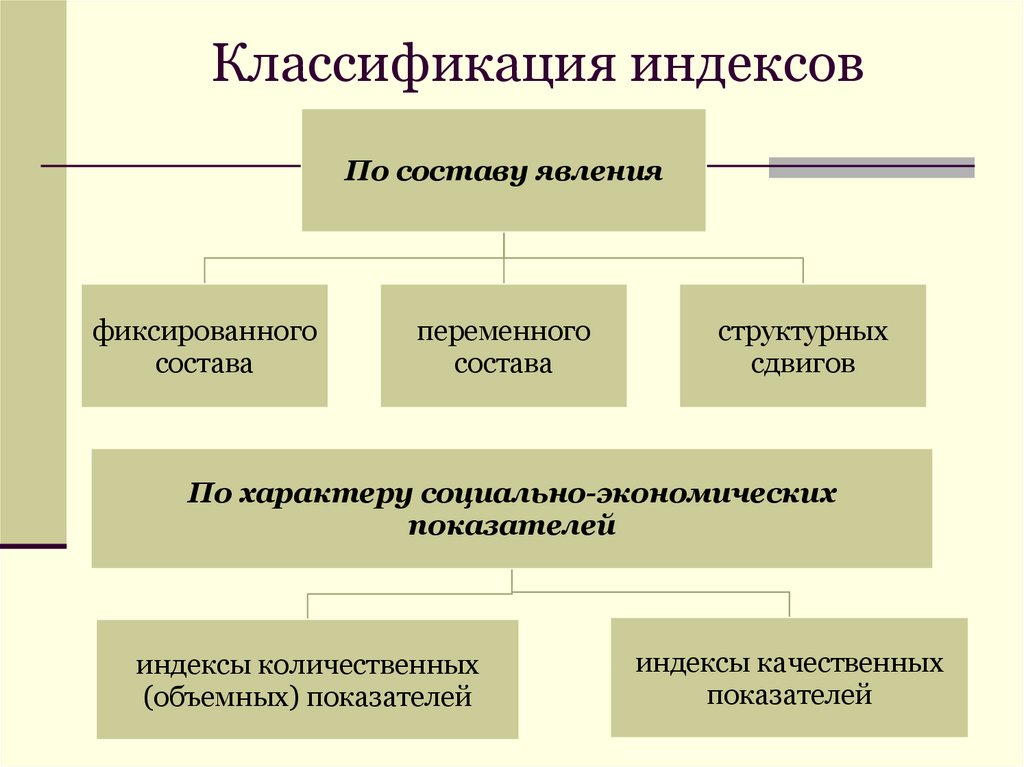
5. Классификация индексов

По составу явления
фиксированного
состава
переменного
состава
структурных
сдвигов
По характеру социально-экономических
показателей
индексы количественных
(объемных) показателей
индексы качественных
показателей

6. Классификация индексов

По базе сравнения
территориальные
динамики
цепные
базисные

7. ОБОЗНАЧЕНИЯ

i
I
q
индивидуальный индекс
t
затраты труда (рабочего времени) на единицу
продукции
р
z
pq
zq
цена за единицу продукции
сводный (общий) индекс
количество продукции одного вида в натуральном
выражении
себестоимость единицы продукции
товарооборот
затраты на производство продукции

8. 2. Индивидуальные и сводные индексы

Индивидуальные - характеризуют
изменение только одного элемента
совокупности
Сводные (общие) - характеризуют
изменение по всей совокупности
элементов сложного явления

9. Индивидуальные индексы 1. Динамические

цены
p1
ip ,
p0
q1
,
физического объема iq
q0
товарооборота
p1 q1
i pq
i p iq.
p0 q0

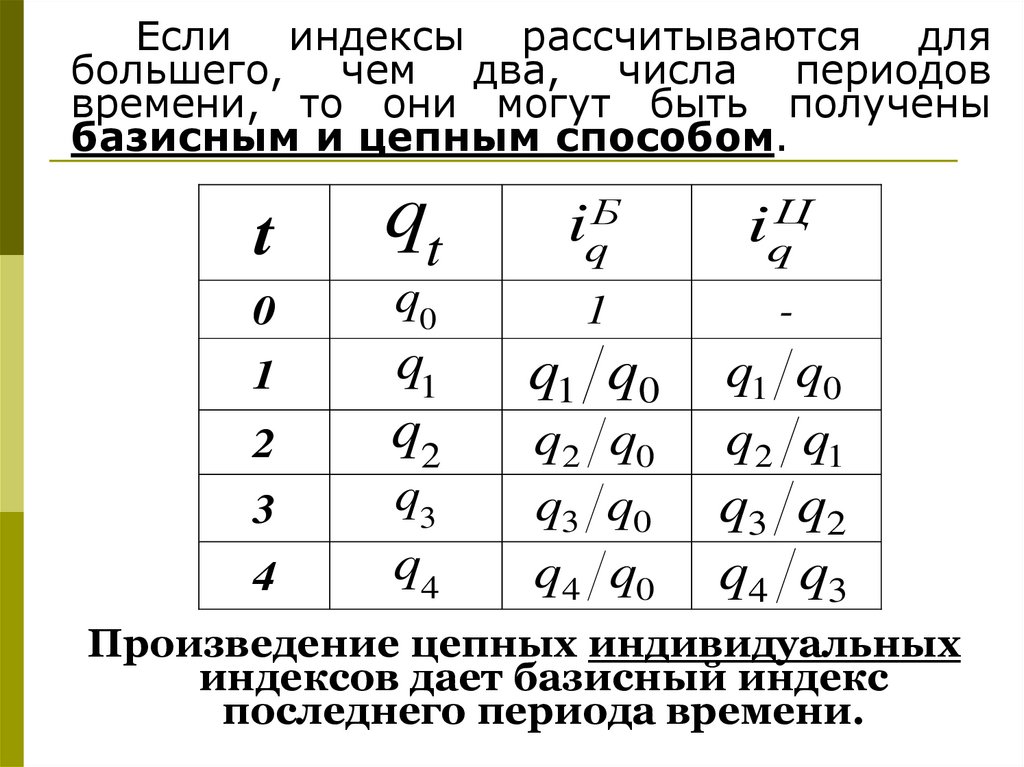
10.

Если индексы рассчитываются для
большего, чем два, числа периодов
времени, то они могут быть получены
базисным и цепным способом.
t
qt
iqБ
iqЦ
0
q0
1
-
1
q1
2
q2
q1 q0
q1 q0
q2 q1
3
q3
4
q4
q2 q0
q3 q0
q4 q0
q3 q2
q4 q3
Произведение цепных индивидуальных
индексов дает базисный индекс
последнего периода времени.

11. Индивидуальные индексы 2. Выполнения плана

себестоимости
z1
iz
,
zпл
q
физического объема i 1 ,
q
qпл
z
q
1
1 i i .
общих затрат i
zq
z q
zпл qпл

12. Сводные (общие) индексы

Сводный
индекс
—
это
сложный
относительный
показатель,
который
характеризует
среднее
изменение
социально-экономического
явления,
состоящего
из
непосредственно
несоизмеримых элементов.
Агрегатные
Средние взвешенные

13. Основные агрегатные индексы (относительное изменение)

Агрегатный индекс цены:
Ip
pq
p q
1
1
0
1
Агрегатный
объема:
q p
I
q p
1
0
0
0
индекс
физического
q
Агрегатный
индекс
стоимости (товарооборота):
I pq
pq
p q
1
1
0
0
I pq I p I q
общей

14. Основные агрегатные индексы (абсолютное изменение)

•Товарооборота
в том числе за счет:
pq p1 q1 p0 q0
•изменения цен
p
pq p1 q1 p0 q1
•изменения
количества
проданных товаров
q
pq p0 q1 p0 q0
p
q
pq pq pq

15. Расчет индекса цен в агрегатной форме возможен в двух вариантах:

1.
Количество
проданных
товаров
фиксируется на уровне отчетного периода:
p1 q1
П
Ip
, где
p0 q1
I pП - индекс Пааше.
2.
Количество
проданных
товаров
фиксируется на уровне базисного периода:
p1 q0
Л
Ip
, где
p0 q0
I pЛ - индекс Ласпейреса.

16. Для получения единого результата используется индекс Фишера

Ф
Ip
П Л
I p I p .

17.

Задачи по экономическим
индексам 1

18. Территориальные индексы

Позволяют сравнивать один и тот же
индексируемый показатель по двум
разным объектам или территориям
(объекты А и Б, например).
При их построении в качестве весов
могут использоваться показатели
как для региона А, так и для региона
Б, суммарные или средние
показатели.

19. Территориальные индексы цен

В качестве весов принимаются объемы проданных
товаров по двум регионам вместе взятым:
Q qa qb
Территориальный индекс цен в этом случае
рассчитывается по следующей формуле:
pbQ
I pb
pa Q
a

20.

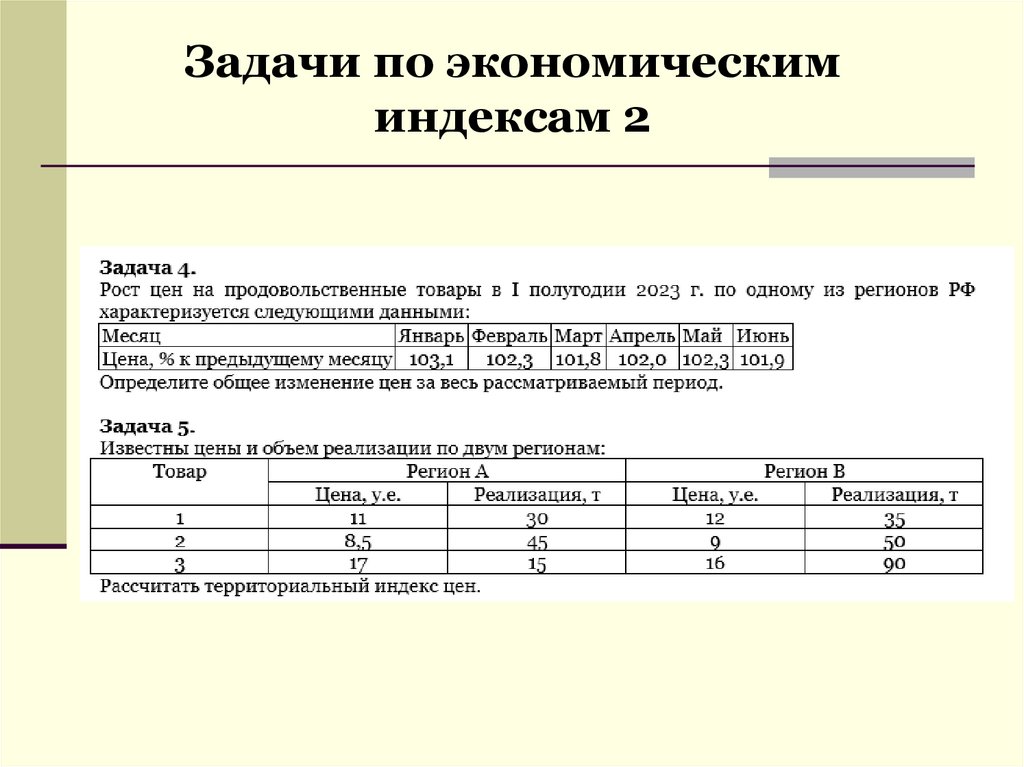
Задачи по экономическим
индексам 2