Свойства дисперсии. § 17

1.

§ 17. Свойства дисперсии
1) Дисперсия постоянной величины C равна нулю:
D C 0 .
2) Постоянный множитель можно выносить за знак дисперсии,
возведя его в квадрат:
D CX C 2 D X .
3) Дисперсия суммы двух независимых случайных величин X и Y
равна сумме дисперсий этих величин
D X Y D X D Y .
Следствие. Дисперсия суммы нескольких взаимно независимых
случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин X и Y
равна сумме дисперсий этих величин
D X Y D X D Y .

2.

§ 19. Среднее квадратическое отклонение суммы взаимно
независимых величин
Средним квадратическим отклонением X случайной величины
X называют квадратный корень из ее дисперсии
( X ) D ( X ) .
Среднее квадратическое отклонение имеет размерность случайной
величины.
Теорема. Среднее квадратическое отклонение суммы конечного
числа взаимно независимых случайных величин равно квадратному
корню из суммы квадратов средних квадратических отклонений этих
величин:
X 1 X 2 ... X n 2 X 1 2 X 2 ... 2 X n .

3.

§ 20. Одинаково распределенные взаимно независимые
случайные величины
Если несколько случайных величин имеют одинаковые законы
распределения, то их числовые характеристики одинаковы.
Пусть X 1 , X 2 ,..., X n – взаимно независимые случайные величины,
которые имеют одинаковые распределения и, следовательно,
X
одинаковые
характеристики.
Среднее
арифметическое
рассматриваемых случайных величин равно
X 1 X 2 ... X n
.
X
n
Теорема 1. Математическое ожидание среднего арифметического
одинаково распределенных взаимно независимых случайных величин
равно математическому ожиданию a каждой из величин:
M X a .
Доказательство. Так как постоянный множитель можно выносить за
знак математического ожидания и математическое ожидание суммы
равно сумме математических ожиданий слагаемых, получим
X 1 X 2 ... X n M X 1 M X 2 ... M X n na
M X M
a
n
n
n

4.

Теорема 2. Дисперсия среднего арифметического n одинаково
распределенных взаимно независимых случайных величин в n раз
меньше дисперсии D каждой из величин:
D
D X .
n
Доказательство. Так как постоянный множитель можно выносить
за знак дисперсии, возведя его в квадрат, и дисперсия суммы равна
сумме дисперсий слагаемых, получим
X X 2 ... X n D X 1 D X 2 ... D X n nD D
D X D 1
2 .
2
n
n
n
n
Теорема 3. Среднее квадратическое отклонение среднего
арифметического n одинаково распределенных взаимно независимых
случайных величин в
n раз меньше среднего квадратического
отклонения каждой из величин:
X
.
n
Доказательство. Так как D X D n , получим
X D X
D
.
n
n

5.

Следовательно, среднее арифметическое нескольких измерений
ближе к истинному значению измеряемой величины, чем результат
отдельного измерения.
Пример. Среднее квадратическое отклонение отдельного измерения
равно 4 атм , всего произведено n=16 измерений. Тогда среднее
квадратическое отклонение среднего арифметического измерений равно
4
X
1 атм.
n
16
§ 21. Понятие о моментах распределения
Начальным моментом k порядка k случайной величины X
называют математическое ожидание величины Xk:
k M X k .
Например:
1 M X , 2 M X 2 , 3 M X 3 , … .
Следовательно, можно написать:
D X M X 2 M 2 X 2 12 .

6.

§ 18. Дисперсия числа появлений события в независимых
испытаниях
Рассмотрим случайную величину X – число появлений события A в
n независимых испытаниях.
Теорема. Дисперсия случайной величины X – числа появлений
события A в n независимых испытаниях с одинаковой вероятностью p –
равна
D X npq .
Так как величина X распределена по биномиальному закону, то
можно сказать, что: дисперсия случайной величины X, распределенной по
биномиальному закону с параметрами n и p равна
D X npq .
Пример. Вероятность сдачи зачета равна p 0,4 . Найти
дисперсию числа сдач зачета, если будет сделано 5 попыток.
Решение. Сдача зачета при каждой попытке не зависит от исходов
других попыток. Поэтому сдачи зачета – события независимые и
D X npq 5 0,4 0,6 1,2 .

7.

Центральным моментом k порядка k случайной величины X
называют математическое ожидание величины X M X k :
k M X M X k .
Например:
1 M X M X 0 ,
2 M X M X ,
2
3 M X M X ,
….
3
Можно доказать, что:
2 2 12 D X ,
3 3 3 1 2 2 13 .
4 4 4 1 3 6 12 2 3 14 .

8.

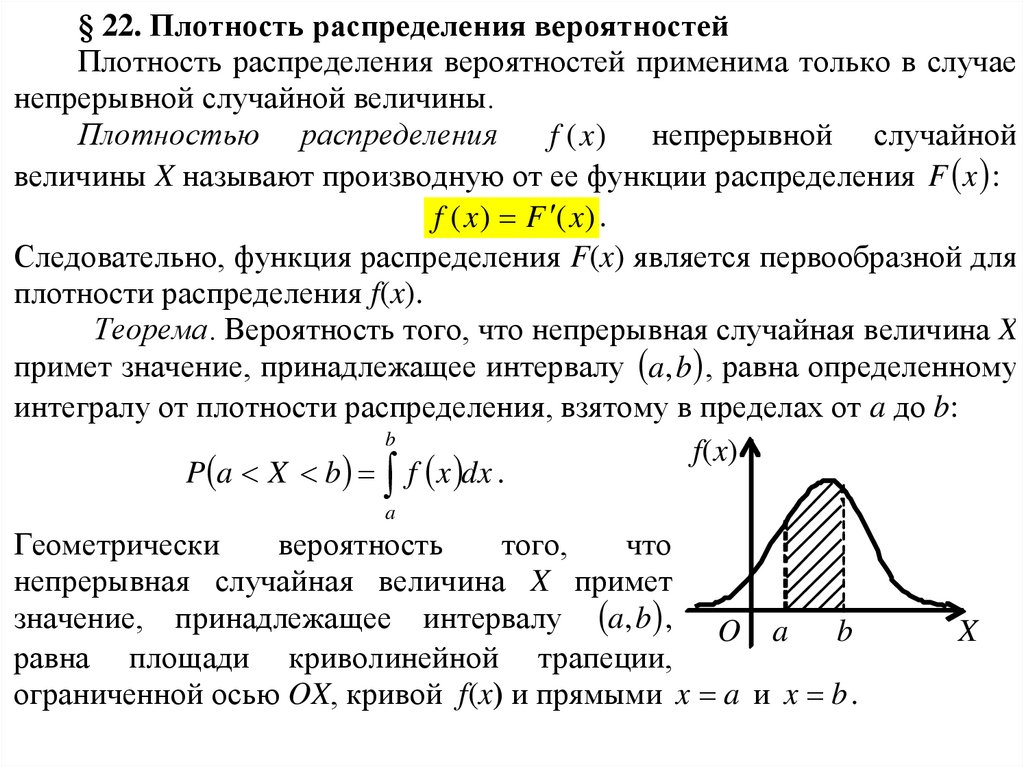
§ 22. Плотность распределения вероятностей
Плотность распределения вероятностей применима только в случае
непрерывной случайной величины.
Плотностью распределения
f (x ) непрерывной случайной
величины X называют производную от ее функции распределения F x :
f ( x ) F ( x ) .
Следовательно, функция распределения F(x) является первообразной для
плотности распределения f(x).
Теорема. Вероятность того, что непрерывная случайная величина X
примет значение, принадлежащее интервалу a, b , равна определенному
интегралу от плотности распределения, взятому в пределах от a до b:
b
f(x)
P a X b f x dx .
a
Геометрически
вероятность
того,
что
непрерывная случайная величина X примет
значение, принадлежащее интервалу a, b , O a
b
равна площади криволинейной трапеции,
ограниченной осью OX, кривой f(x) и прямыми x a и x b .
X

9.

Пример. Задана плотность распределения вероятностей случайной
0 при x 0
величины X: f ( x) 2 x при 0 x 1 . Найти вероятность того, что
0 при x 1
случайная величина X примет значение X 0,2; 0,4 .
0, 4
Решение. P 0,2 X 0,4 2 xdx x
0, 2
2 0, 4
0, 2
0,16 0,04 0,12 .
Теорема. Зная плотность распределения f(x) можно найти функцию
распределения F(x) по формуле
x
F x f x dx .
Пример. Найти функцию распределения по данной плотности
при x a
0
1
распределения f ( x )
при a x b .
b a
при x b
0

10.

x
Решение. F x f x dx . Следовательно:
при x a
a
a
F x f x dx 0 dx 0 ,
1
x a
,
F x f x dx f x dx 0
dx
b a
b a
a
a
a
при a x b
x
b a
F x f x dx f x dx f x dx 0
0 1.
b a
a
b
a
при x b
x
b
x
при x a
0
x a
Итак, имеем F ( x )
при a x b .
b a
при x b
1