Числовые характеристики случайных величин. Лекция 7

1. Числовые характеристики случайных величин

Лекция 7

2. Числовые характеристики случайных величин

Закон
распределения
и
плотность
распределения
характеризует случайную величину. Однако при решении многих
практических задач достаточно знать лишь некоторые числовые
параметры, характеризующие отдельные существенные свойства
закона распределения случайной величины. Такие числа принято
называть числовыми характеристиками случайной величины.
Важнейшими среди них являются характеристики положения:
математическое
ожидание
(центр
распределения
случайной
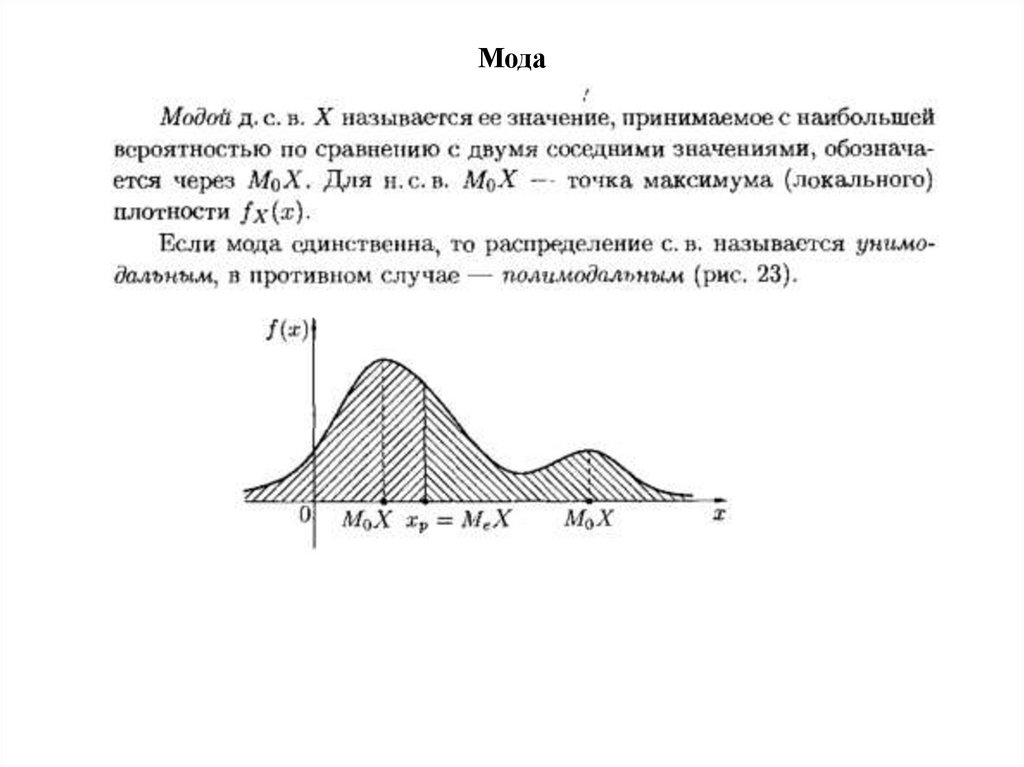
величины), мода, медиана; характеристики рассеяния: дисперсия
(отклонение случайной величины от ее центра),
квадратическое отклонение.
среднее

3. Математическое ожидание случайной величины

Математическим
ожиданием
(или
средним
значением)
дискретной случайной величины Х имеющей закон распределения
pi P{ X xi }, i 1,2,3,..., n называется число, равное сумме произведений
всех ее значений на соответствующие им вероятности.
Математическое ожидание обозначается через МХ (или М/Х,
М(Х), ЕХ, mX , a X ). Таким образом, по определению
n
MX xi pi .
i 1
(1)
Если число возможных значений случайной величины
бесконечно (счетно), то
MX xi pi ,
i 1
причем
(2)
ряд в правой части предполагается сходящимся ( в
противном случае случайная величина Х не имеет математического
ожидания).

4. Математическое ожидание случайной величины

Вероятностный смысл математического ожидания состоит в том,
что оно является средним значением случайной величины.
n
Действительно, так как pi 1 , то
i 1
n
n
MX xi pi
i 1
x p
i 1
n
p
i 1
Математическим
i
i
xсреднее .
i
ожиданием
непрерывной
случайной
величины с плотностью вероятности f (x) , называется число
MX x f ( x)dx .
(3)
Интеграл в правой части равенства (3) предполагается абсолютно
сходящимся, т.е.
x f ( x)dx
в противно случае непрерывная случайная величина Х не имеет
математического ожидания.

5. Свойства математического ожидания

1. Математическое ожидание постоянной равно самой этой
постоянной, т.е.
2. Постоянный
MC C .
множитель
выносится
за
знак
математического ожидания, т.е. M (CX ) CMX .
3. Математическое ожидание суммы случайных величин
равно
сумме
математических
ожиданий,
т.е.
M ( X Y ) MX MY .
4. Математическое
ожидание
отклонения
случайной
величины от ее математического ожидания равно нулю,
т.е. M ( X MX ) 0 .
5. Математическое ожидание произведения независимых
случайных величин равно произведению их математических
ожиданий, т.е. если X и Y независимы, то M ( X Y ) MX MY .

6. Доказательство свойств математического ожидания

7. Доказательство свойств математического ожидания

8. Доказательство свойств математического ожидания

9. Пример

В лотерее имеется 1000 билетов, из них выигрышных: 10 по
500 руб., 50 по 50 руб., 100 по 10 руб., 150 по 1 руб. Найти
математическое ожидание выигрыша на один билет.

10. Дисперсия

Дисперсией (рассеянием) случайной величины Х называется
математическое ожидание квадрата ее отклонения от своего
математического ожидания.
Обозначается дисперсия через
DX , D[ X ], DX , D( X ) .
Таким
образом, по определению DX M ( X MX ) 2 . Дисперсия характеризует
разброс значений случайной величины Х от ее математического
ожидания. Из определения дисперсии следуют формулы для ее
вычисления:
DX MX 2 (MX ) 2 .
(4)

11. Дисперсия

Это позволяет записать формулу для ее вычисления в другом
виде:
DX xi2 pi (MX ) 2 ,
i
DX x 2 f ( x)dx ( MX ) 2 .

12. Свойства дисперсии

1. Дисперсия постоянной величины равна нулю, т.е. DC 0 .
2. Постоянный
множитель
можно
выносить
за
знак
дисперсии, возведя его в квадрат, т.е. DCX C 2 DX .
3. Дисперсия суммы независимых случайных величин равна
сумме их дисперсий, т.е. если
и
X
Y независимы,
то
D( X Y ) DX DY .
4. Дисперсия не изменится, если к этой случайной величине
прибавить постоянную, т.е. D( X C ) DX .
5. Если
случайные
величины
D( XY ) MX 2 MY 2 ( MX ) 2 ( MY ) 2 .
X
и
Y независимы,
то

13. Доказательства свойств

1. DC M (C MC ) 2 M (C C ) 2 M 0 0 .
2. D(CX ) M (CX M (CX )) M (C( X MX )) M (C ( X MX ) ) C M ( X MX ) C DX .
2
2
2
2
2
2
3. Используя формулу (3), получаем
D( X Y ) M ( X Y ) 2 ( M ( X Y )) 2 MX 2 2M ( XY ) MY 2 ( MX ) 2
2MXMY ( MY ) 2 MX 2 ( MX ) 2 MY 2 ( MY ) 2 2( M ( XY ) MXMY )
DX DY 2( MXMY MXMY ) DX DY
4. D(C X ) M ((C X ) M (C X )) 2 M ( X MX ) 2 DX .
2

14. Среднее квадратическое отклонение

Дисперсия DX имеет размерность квадрата случайной величины,
что в сравнительных целях неудобно. Когда желательно, чтобы
оценка
разброса
используют еще
имела
размерность
одну числовую
случайной
величины,
характеристику- среднее
квадратическое отклонение.
Средним квадратическим отклонением случайной величины Х
называется квадратный корень из ее дисперсии, обозначают через
X , , [ X ] .
Таким образом, по определению
DX
.
Для изучения свойств случайного явления, независящих от
выбора масштаба измерения и положения центра группирования,
исходную случайную величину Х приводят к стандартному виду,
т.е записывают разность X MX . Геометрически это означает, что
начало координат переносится в точку с абсциссой, равной
математическому
ожиданию,
квадратическое отклонение X .
затем
делят
на
среднее

15. Среднее квадратическое отклонение

Случайную величину
Z
X MX
X
называют стандартной
случайной величиной. Ее математическое ожидание рано нулю, а
дисперсия равна единице. Действительно
X MX
1
MZ M
M ( X MX ) 0 ,
X X
X MX
1
DX
2 D( X MX )
DZ D
1.
DX
X X
То есть Z - центрированная ( MZ 0 ) и нормированная ( DZ 1 )
случайная величина.
Пример. Дискретная случайная величина задана рядом
распределения
Х
-1
0
1
2
р
0,2
0,1
0,3
0,4
Найти MX , DX , X .

16. Мода

17. Медиана

18. Начальные и центральные моменты

19. Начальные и центральные моменты

20. Коэффициенты асимметрии и эксцесса

21. Коэффициенты асимметрии и эксцесса

22. Квантили уровня