Ряды динамики и их анализ

1. РЯДЫ ДИНАМИКИ И ИХ АНАЛИЗ

.
1. Понятие о динамических рядах. Виды
рядов динамики
2. Показатели анализа ряда динамики
3. Аналитическое выравнивание
динамических рядов
4. Основные методы прогнозирования
рядов динамики

2. динамические ряды

Известно, что социально-экономические явления
находятся в постоянном развитии во времени. Изучение
процесса развития этих явлений - одна из основных задач
статистики, которая решается путем построения и
анализа рядов динамики.
Динамика означает изменение процессов во времени,
поэтому ряд статистических показателей,
характеризующий изменение общественных явлений во
времени называется динамическим рядом.
Показатели, из которых состоит динамический ряд
называются уровнями динамического ряда и
обозначаются - У, а период времени, за который они
представлены - t.

3. Составляющие ряда

Каждый динамический ряд содержит две
составляющие:
1) показатели периодов времени (годы,
кварталы, месяцы, дни или даты);
2) показатели, характеризующие
исследуемый объект за временные
периоды или на соответствующие даты,
которые называют уровнями ряда.

4. Виды

По времени различают моментные и интервальные ряды
динамики.
В моментных рядах уровни выражают состояние явления на
критический момент времени – начало месяца, квартала, года и
т.д. Например, численность населения, численность работающих и
т.д. В таких рядах каждый последующий уровень полностью или
частично содержит значение предыдущего уровня, поэтому
суммировать уровни нельзя, так как это приводит к повторному
счету.
В интервальных – уровни отражают состояние явления за
определенный период времени – сутки, месяц, год и т.д. Это
ряды показателей объема производства, объема продаж по месяцам
года, количества отработанных человеко-дней и т.д.

5. Форма

По форме представления
уровней различают ряды абсолютных,
относительных и средних величин

6. система показателей ряда

применяется система показателей ряда
динамики, которая может быть
представлена следующей группой
показателей:
1. Абсолютный прирост
2. Темп роста
3. Темп прироста
4. Значение 1% прироста.

7. базисный или цепной

В основе расчета показателей рядов динамики лежит
сравнение его уровней. В зависимости от применяемого
способа сопоставления (базисный или цепной)
показатели динамики могут вычисляться на постоянной и
переменной базах сравнения.
Для расчета показателей на постоянной базе
(базисный способ расчета) каждый уровень ряда
сравнивается с одним и тем же базисным уровнем.
Исчисляемые при этом показатели называются
базисными.
Для расчета показателей на переменной базе (цепной
способ расчета) каждый последующий уровень ряда
сравнивается с предыдущим. И показатели называются
цепными.

8. абсолютный прирост

который показывает абсолютную скорость роста
или снижения сравниваемых уровней, и
рассчитывается как разность между этими
уровнями (между последующим и предыдущим
уровнем, принятым за базу сравнения).
Измеряется в тех же единицах, что и исходная
информация.
А = Y1 – Y0,
где Y1 – значение отчетного уровня ряда
динамики;
Y0 – значение базисного уровня ряда
динамики.

9. пример

Пусть мы имеем следующий ряд динамики производства продукции в 1990-1993 г.г.
Год (t)
1990
1991
1992
1993
Уровень производства
12,3
14,1
12,6
17,8
продукции, тыс. руб. (Y)
На основании данного ряда динамики рассчитаем базисные (приняв за базу сравнения 1990 год)
и цепные абсолютные приросты:
Базисные: А91/90=Y91-Y90; А92/90= Y92-Y90; А93/90=Y93-Y90
Цепные:
А91/90=Y91-Y90; А92/91= Y92-Y91; А93/92=Y93-Y92
Между цепными и базисными абсолютными приростами имеется следующая взаимосвязь: сумма
цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда
динамики:
А93/90=Y93-Y90=A91/90+A92/91+A93/92.

10. Темп

Темп (коэффициент) роста показывает
относительную скорость роста уровня ряда
динамики и представляет собой отношение
каждого последующего уровня к предыдущему,
принятому за базу сравнения. Темп роста
измеряется в %, а коэффициент роста - в долях.
Между цепными и базисными темпами роста
имеется взаимосвязь:А93/90=Y93Y90=A91/90+A92/91+A93/92.
Произведение последовательных цепных темпов
роста равно базисному темпу роста последнего
периода:
Y93
93 / 90
91 / 90
92 / 91
93 / 92
Тр
Y90
* 100 Т р
* Тр
* Тр

11. Цепной

1. Частное от деления последующего базисного темпа роста на предыдущий равно
соответствующему цепному темпу роста:
Т р 93 / 90
Тр
93 / 92
Т
р
92 / 90
Y 93
Y
92
*100 .

12. Темп прироста

Темп (коэффициент) прироста показывает на сколько процентов изменился сравниваемый
уровень с уровнем, принятым за базу сравнения:
Y1 Y0
Т пр
*100 ,
Y0
Y1 Y0
К пр
.
Y0
Между темпом (коэффициентом) прироста и темпом (коэффициентом) роста существует
следующая взаимосвязь:
Тпр=Тр-100,
Кпр=Кр-1.

13. Значение 1 % прироста

Значение 1 % прироста определяется отношением абсолютного прироста к темпу прироста, и
показывает сколько единиц в абсолютном выражении приходится на 1% прироста для данного ряда
динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он не
имеет смысла (будет постоянной величиной).
Y1 Y0
Y0
А
1%
0,01* Y0 .
Т пр Y1 Y0
100
*100
Y0

14. Средний уровень ряда динамики

1. Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
В интервальных рядах динамики средний уровень определяется по формуле средней
арифметической:
Y
- простой Y
;
n
Y*t
- взвешенной Y
,
t
где Y - сумма уровней; n – число уровней.

15. Моментный ряд

Для моментного ряда средний уровень определяется с помощью средней хронологической:
1
1
* Y1 Y2 ... * Yn
2
Y 2
, где n – число уровней.
n 1

16. Средний абсолютный прирост

2. Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных
абсолютных приростов ряда динамики. При цепном способе для определения среднего абсолютного
прироста сумма цепных абсолютных приростов делится на их число:
ц
А
Ац
.
n
При базисном способе расчета чтобы определить средний абсолютный прирост, для этого
определяется разность между конечным Уn и базисным У0 уровнями изучаемого периода, которая
делится на m-1 субпериодов:
Yn Y0
А
.
m 1
б

17.

3. Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики.
Для определения среднего темпа роста цепным способом применяется следующая формула:
ц
Т р n Кр1 * Кр 2 * ... * Кр n *100,
где Кр1, Кр2, ..., Крn - индивидуальные (цепные) коэффициенты роста;
n - число индивидуальных темпов роста
Для базисного способа средний темп роста будет определяться по формуле:
б
Т р m 1
Yn
* 100 .
Y0
4. Средний темп прироста можно определить по формуле: Тпр Тр 100 .

18. Среднее значение 1% прироста

5. Среднее значение 1 % прироста определяется только для цепного способа по формуле:
1%
Ац
Т пр
ц
.
Эти показатели динамики находят практическое применение во всех расчетах, где требуется изучение
изменения социально-экономических явлений во времени.

19. изучение общей тенденции развития (тренда).

На практике наиболее распространенными
методами статистического изучения тренда
являются: способ укрупнение интервалов
(периодов), способ сглаживания скользящей
средней, выравнивание ряда по среднегодовому
абсолютному приросту, выравнивание ряда по
среднегодовому темпу роста, аналитическое
выравнивание при помощи способа наименьших
квадратов.

20. Способ укрупнения интервалов

применяется для выявления тренда в рядах
динамики колеблющихся уровней,
затушевывающих основную тенденцию развития.
Сущность этого приема состоит в том, что данные
или уровни за отдельные отрезки времени
суммируются в ряды более продолжительных
периодов (месячные в квартальные, квартальные
в годовые), определяется средний уровень для
полученного укрупненного периода. В результате
после укрупнения периодов очевидной
становится тенденция развития явления.

21. Укрупнение рядов

По данным об производстве продукции проведите выравнивание ряда динамики
способом укрупненных периодов, скользящей средней и аналитическим
выравниванием по прямой. Произведите прогнозирование производства продукции с
помощью уравнения основной тенденции.
Пример 1. Имеются следующие данные о динамики производства продукции
Год
2001 2002 2003 2004 2005 2006 2007 2008 2009
Производство
23
19
21
20
22
21
25
19
24
продукции, млн. руб.

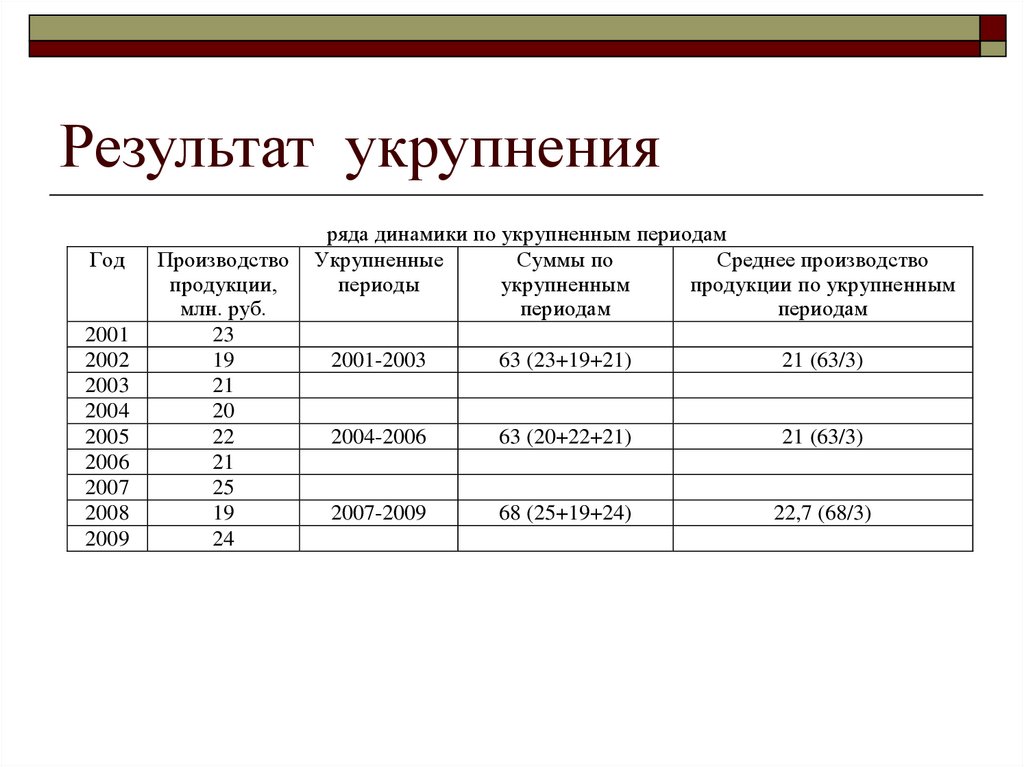
22. Результат укрупнения

Год
2001
2002
2003
2004
2005
2006
2007
2008
2009
Производство
продукции,
млн. руб.
23
19
21
20
22
21
25
19
24
ряда динамики по укрупненным периодам
Укрупненные
Суммы по
Среднее производство
периоды
укрупненным
продукции по укрупненным
периодам
периодам
2001-2003
63 (23+19+21)
21 (63/3)
2004-2006
63 (20+22+21)
21 (63/3)
2007-2009
68 (25+19+24)
22,7 (68/3)

23. Способ скользящей средней

. Скользящая средняя - это подвижная
динамическая средняя, которая подсчитывается
по динамическому ряду при последовательном
передвижении на 1 год или на 1 интервал.
Правильно исчисленная скользящая средняя
устраняет в ряду динамики случайные
колебания и дает возможность точнее выявить
тенденцию в развитии, чем укрупненные
интервалы.

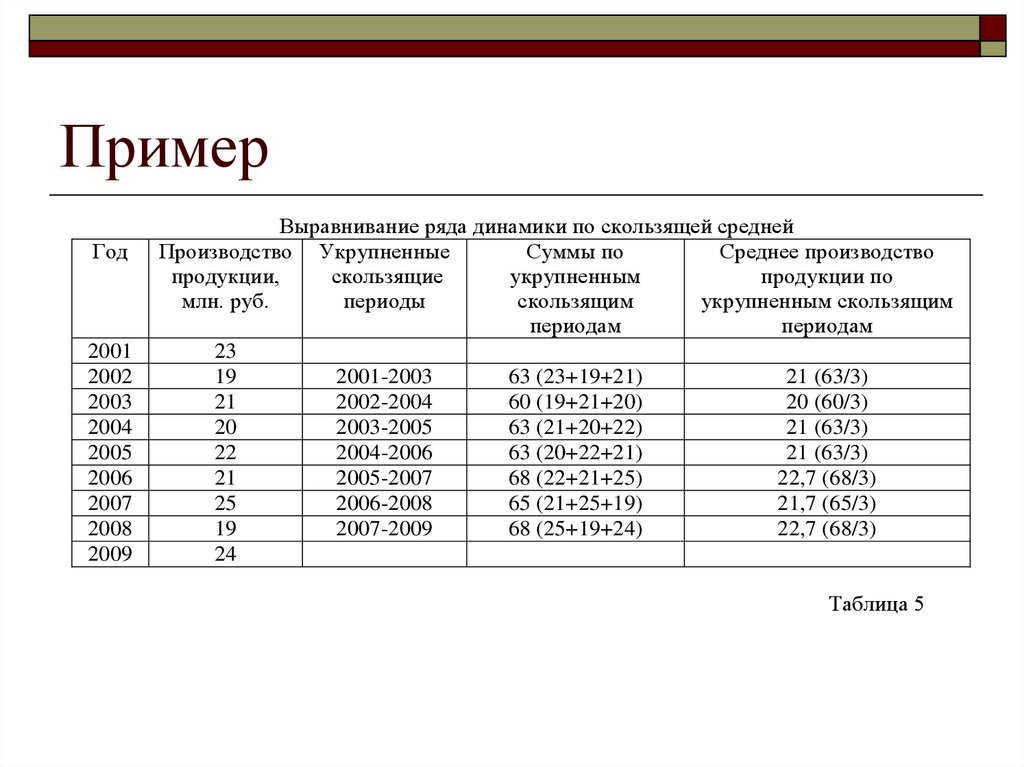
24. Пример

Год
2001
2002
2003
2004
2005
2006
2007
2008
2009
Выравнивание ряда динамики по скользящей средней
Производство Укрупненные
Суммы по
Среднее производство
продукции,
скользящие
укрупненным
продукции по
млн. руб.
периоды
скользящим
укрупненным скользящим
периодам
периодам
23
19
2001-2003
63 (23+19+21)
21 (63/3)
21
2002-2004
60 (19+21+20)
20 (60/3)
20
2003-2005
63 (21+20+22)
21 (63/3)
22
2004-2006
63 (20+22+21)
21 (63/3)
21
2005-2007
68 (22+21+25)
22,7 (68/3)
25
2006-2008
65 (21+25+19)
21,7 (65/3)
19
2007-2009
68 (25+19+24)
22,7 (68/3)
24
Таблица 5

25. Выравнивание

3. Еще более точным способом является выравнивание по среднегодовому абсолютному приросту,
которое рассчитывается по формуле:
~
~
Yt Y0 A t ,
где Yt - выровненное значение;
Y0 - начальный уровень ряда;
А - средний базисный абсолютный прирост, который вычисляется по формуле:
б Yn Y0
А
,
n 1
где n - число лет;
t - порядковый номер года, в котором были приросты.

26. Использование коэффициента роста

4. Выравнивание ряда по среднегодовому коэффициенту роста имеет следующий вид:
t
~
Yt Y0 Кр ,
~
где Yt - выровненное значение;
Y0 - начальный уровень ряда
Кр - среднегодовой базисный коэффициент роста, определяемый по формуле:
Кр
n – число лет;
t - порядковый номер года.
б
Yn
n 1 ,
Y0

27. Линейная зависимость

5. Способом аналитического выравнивания можно получить обобщенную статистическую оценку
тренда. Наиболее совершенным является способ наименьших квадратов, которому соответствует
условие, что сумма квадратов отклонений фактического и теоретического уровней будет
минимальной. Простейшим приемом является выравнивание ряда динамики по прямой:
~
Yt а b t ,
где а - свободный член;
b - коэффициент приращения;
t - период времени.

28. Зависимости

29. Уравнения для расчета

Способ наименьших квадратов дает систему двух нормальных уравнений для вычисления параметров
функции:
Y a *n b* t ,
где Y – исходные уровни ряда;
n – число членов ряда;
t – время.
2
Y
a
*
t
b
*
t
t
,

30. Оценка времени

Для упрощения вычислений показателям времени t придают такие значения, чтобы их сумма была
равна нулю ( t 0 ). При этом используют следующие формулы:
-
если ряд содержит четное число членов t ч 2 * k (n 1)
-
если ряд содержит нечетное число членов t н / ч k
где k – порядковый номер года;
n – число лет в периоде.
n 1
,
2

31. Расчет коэффициентов

При t 0 система уравнений будет иметь следующий вид:
Y a*n,
Yt b * t 2 .
Исходя из полученной системы уравнений найдем параметры уравнения прямой:
Y
а
,
b
n
Yt
t
2
.

32. Метод наименьших квадратов

В большинстве расчетов используют метод наименьших
квадратов, который обеспечивает наименьшую сумму
квадратов отклонений фактических уровней от выравненных:
Для линейной зависимости (f(t)=a0+a1(t) параметр а0 обычно
интерпретации не имеет, но иногда его рассматривают как
обобщенный начальный уровень ряда; а1 - сила связи, т.е.
параметр, показывающий, насколько изменится результат при
изменении времени на единицу. Таким образом, а можно
представить как постоянный теоретический абсолютный
прирост.

33. критерий Фишера

Построив уравнение регрессии, проводят
оценку его надежности. Это делается
посредством критерия Фишера (F).
Фактический уровень (Fфакт)
сравнивается с теоретическим (табличным)
значением:

34.

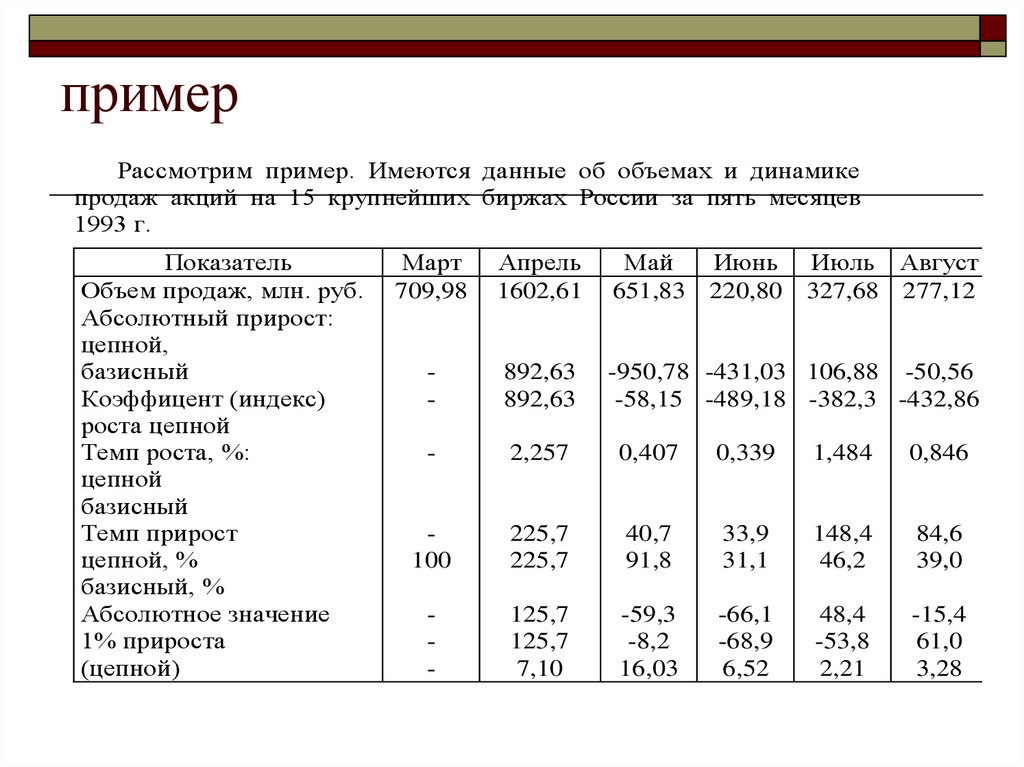
35. пример

Рассмотрим пример. Имеются данные об объемах и динамике
продаж акций на 15 крупнейших биржах России за пять месяцев
1993 г.
Показатель
Объем продаж, млн. руб.
Абсолютный прирост:
цепной,
базисный
Коэффицент (индекс)
роста цепной
Темп роста, %:
цепной
базисный
Темп прирост
цепной, %
базисный, %
Абсолютное значение
1% прироста
(цепной)
Март
709,98
Апрель
1602,61
Май
651,83
Июнь
220,80
Июль Август
327,68 277,12
-
892,63
892,63
-950,78 -431,03 106,88 -50,56
-58,15 -489,18 -382,3 -432,86
-
2,257
0,407
0,339
1,484
0,846
100
225,7
225,7
40,7
91,8
33,9
31,1
148,4
46,2
84,6
39,0
-
125,7
125,7
7,10
-59,3
-8,2
16,03
-66,1
-68,9
6,52
48,4
-53,8
2,21
-15,4
61,0
3,28

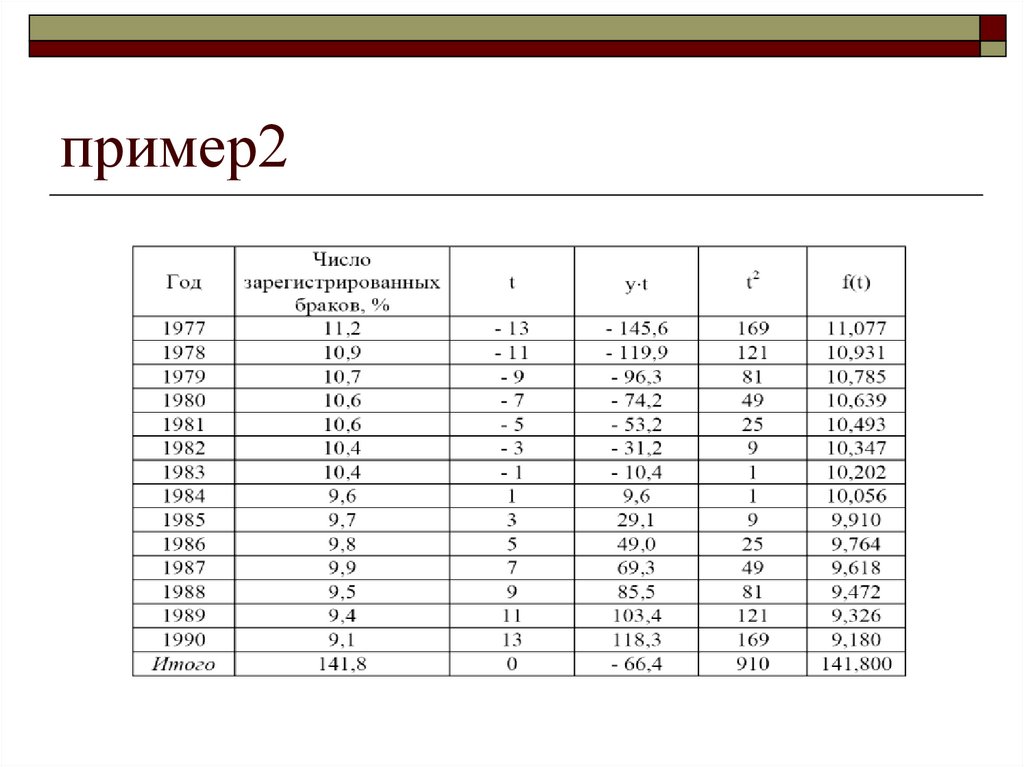
36. пример2

37. пример2

38. Оценка надежности

39. Тест

19. Как называется параметр линейного
уравнения регрессии, стоящей при
факторе?
19.1. Коэффициент вариации
19.2. Коэффициент регрессии
19.3. Коэффициент детерминации
19.4. Коэффициент эластичности

40. Тест

35. Какие показатели динамики
рассчитываются и как базисные и как
цепные?
35.1. Абсолютные приросты и темпы роста
35.2. Абсолютные и относительные
ускорения
35.3. Верно 1 и 2