Теория множеств (продолжение)

1. Теория множеств (продолжение)

1. Теория множеств
(продолжение)

2. 1.2. Операции над множествами

3.

Рассмотрим методы получения новых множеств из уже существующих.
Рассмотрим пространство или множество U и определим в нём 4 операции
над множествами А и В: объединение, пересечение, разность, дополнение.
Объединением А и В называется множество А В, все элементы
которого являются элементами хотя бы одного из множеств А или В:
А В = {x x А или x В}.
Из определения следует, что А А В и В А В.
Аналогично определяется объединение нескольких множеств.
Пример.
1) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А В = {2, 4, 5, 6}.
2) Пусть А – множество чисел, которые делятся на 2, а В – множество
чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А В
множество чисел, которые делятся на 2 или на 3:
А В = {2, 3, 4, 6, 8, 9, 10, …}.

4.

Пересечением множеств А и В называется множество А В, все
элементы которого являются элементами обоих множеств А и В:
А В = {x x А и x В}.
Из определения следует, что А В А, А В В и А В А В.
Аналогично определяется пересечение нескольких множеств.
Пример.
1) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда А В = {4, 6}.
2) Пусть А – множество чисел, которые делятся на 2, а В – множество
чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А В
множество чисел, которые делятся и на 2 и на 3: А В = {6, 12, 18, …}.
Может оказаться, что множества не имеют ни одного общего элемента.
Тогда говорят, что множества не пересекаются или что их пересечение –
пустое множество.
Пример. Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}. Тогда А В C = .

5.

Разностью (относительным дополнением) множества В до множества
А называется множество А \ В, все элементы которого являются элементами
множества А, но не являются элементами множества В:
А \ В = {x x А и x В}.
Пример.
1) А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А= {2}.
2) А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А \ В – множество чисел,
которые делятся на 2, но не делятся на 3, а В \ А – множество чисел,
которые делятся на 3, но не делятся на 2:
А \ В = {2, 4, 8, 10, 14, …}. В \ А= {3, 9, 15, 21, 27, …}.
Симметрической разностью множеств А и В называется множество
А + В: А + В = (А \ В) (В \ А).
Пример.1) А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {5}, В \ А= {2},
А + В = {2, 5}.
2) А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}.
В \ А= {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}.

6.

Дополнением A множества A является множество А={х│х А}.
Пример. Заданы множества А={1, 2, 5, 6} и В={2, 3, 4, 6} на
универсальном множестве U={1, 2, 3, 5, 6, 7}. Выполнить операции А, В.
Решение. В результате выполнения заданных операций получим
следующие множества: А={3, 7}; В={1, 5, 7}.
Также справедливы следующие формулы:
для любых множеств А и В А В = А + В – А В , то есть
учитываются общие для обоих множеств элементы.
Пример. А = {1, 2, 3}
А = 3;
В = {1, 2, 3, 4, 5}
В = 5, тогда
А В = {1, 2, 3, 4, 5} А В = 5; А В = {1, 2, 3} А В = 3,
то есть получим равенство: А В = А + В – А В 5 = 3 + 5 – 3.

7. 1.3. Применение диаграмм Эйлера-Венна при решении практических задач

8.

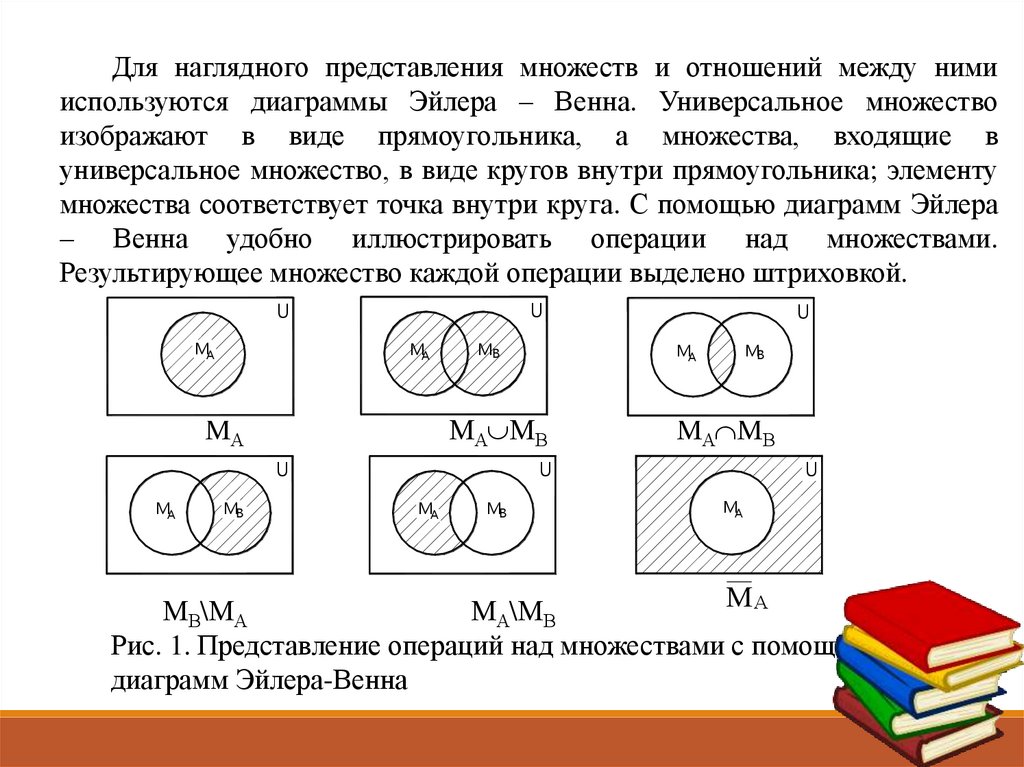
Для наглядного представления множеств и отношений между ними
используются диаграммы Эйлера – Венна. Универсальное множество
изображают в виде прямоугольника, а множества, входящие в
универсальное множество, в виде кругов внутри прямоугольника; элементу
множества соответствует точка внутри круга. С помощью диаграмм Эйлера
– Венна удобно иллюстрировать операции над множествами.
Результирующее множество каждой операции выделено штриховкой.
U
U
MA
MA
MB
MA
MB
MA
U
U
MB
U
U
MA
MB
MA
МА
\
\
Рис. 1. Представление операций над множествами с помощью
диаграмм Эйлера-Венна

9.

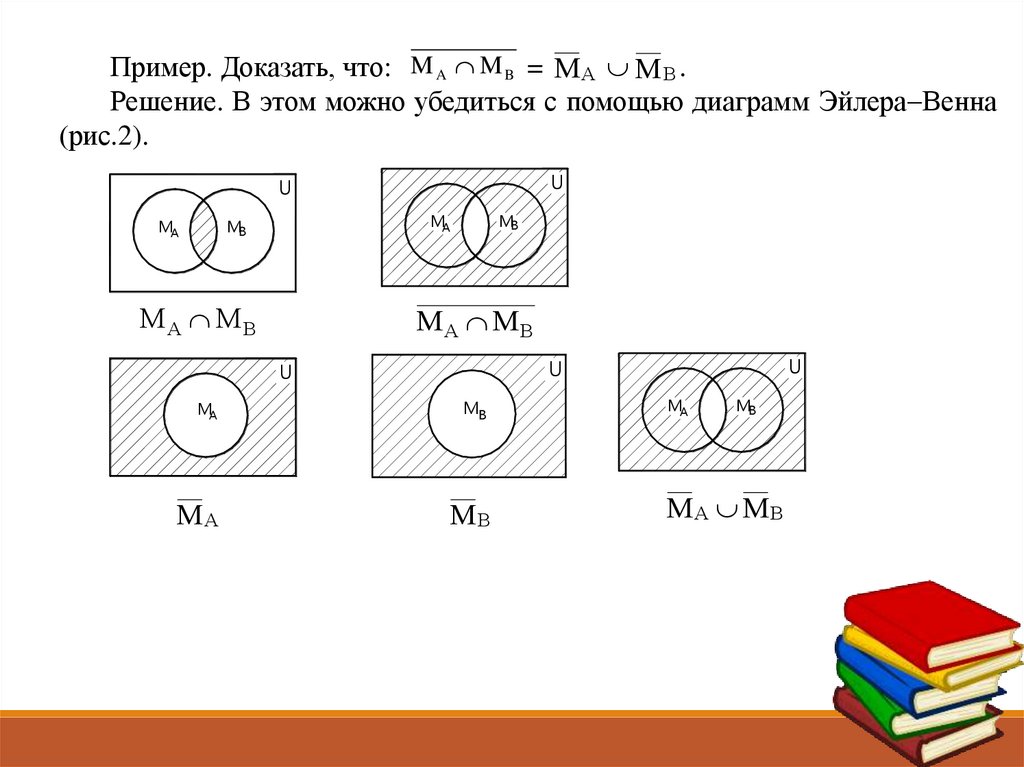
Пример. Доказать, что: M A M B = М А М В .
Решение. В этом можно убедиться с помощью диаграмм Эйлера Венна
рис.2).
U
U
MA
MA
MB
МА МВ
MB
МА МВ
U
U
U
MA
MB
МА
МВ
MA
MB
МА МВ

10.

Для любых подмножеств А, В и С универсального множества U
выполняются следующие тождества (основные тождества алгебры
множеств):
1. А В=В А (коммутативность )
2. А (В С)=(А В) С
(ассоциативность )
3. А (В С)=(А В) (А С)
(дистрибутивность относительно )
4. А =А (свойство нуля)
5. А А= U (свойство дополнения)
6. А А=А
7. А U=U (свойство единицы)
8. A B = А В (закон де Моргана)
9. А (А В)=А (закон поглощения)
10. A =А (инволюция)
11. А\В=А B
1 . А В=В А (коммутативность )
2 . А (В С)=(А В) С
(ассоциативность )
3 . А (В С)=(А В) (А С)
(дистрибутивность относительно )
4 . А =
5 . А А=
6 . А А=А
7 . А U=А
8 . A B = А В (закон де Моргана)
9 . А (А В)=А (закон поглощения)