Электрические цепи постоянного тока. Электротехнические устройства постоянного тока и области применения

1. Название дисциплины Электротехника, основы электроники и электрооборудование химических производств

Программа курса:
Лекции -54 часа;
Лабораторные – 36 часов;
Экзамен
1

2. МОДУЛЬ 1 Лекция №1 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА Электротехнические устройства постоянного тока и области применения

Электрическая энергия постоянного тока может быть получена:
путем преобразования различных видов энергии:
- химической (гальванические элементы и аккумуляторы),
- механической (электромашинные генераторы постоянного тока),
- тепловой (термоэлектрогенераторы),
- лучистой, например световой (фотодиоды, солнечные батареи).
Источниками постоянного тока могут также служить выпрямители –
преобразователи переменного напряжения в постоянное.
Электрическая энергия может быть преобразована в другие виды энергии:
механическую (электрические двигатели постоянного тока),
химическую (установки электролиза, зарядки аккумуляторов),
тепловую (электрические печи, нагреватели),
световую (лампа накаливания, газоразрядные светодиоды и др.).
2

3. Источниками электрической энергии (генерирующими устройствами) называют электротехнические устройства, производящие

электрическую
энергию
Приемниками (потребителями) электрической энергии называются
устройства, потребляющие электрическую энергию.
Применения постоянного тока:
на транспорте (электропоезда, трамваи, троллейбусы, рудничный
транспорт), в подъемно-транспортных машинах, приводе прокатных
станов, так как двигатели постоянного тока обладают хорошими
возможностями для плавного регулирования частоты вращения;
постоянный ток является основой электрохимических процессов, таких
как электролиз. Электролиз широко применяется в гальванотехнике и
гальванопластике;
источники постоянного напряжения широко применяются для питания
устройств автоматики, робототехники, промышленной электроники и
вычислительной техники
.
3

4. Электрическая цепь и ее элементы

Электрическая цепь- это совокупность электротехнических
устройств, состоящая из источников и приемников электрической
энергии, характеризуемых ЭДС Е, током I, напряжением U и
электрическим сопротивлением постоянному току r
(для электротехнических устройств постоянного тока).
Элементы электрической цепи - отдельные устройства, входящие в
электрическую цепь.
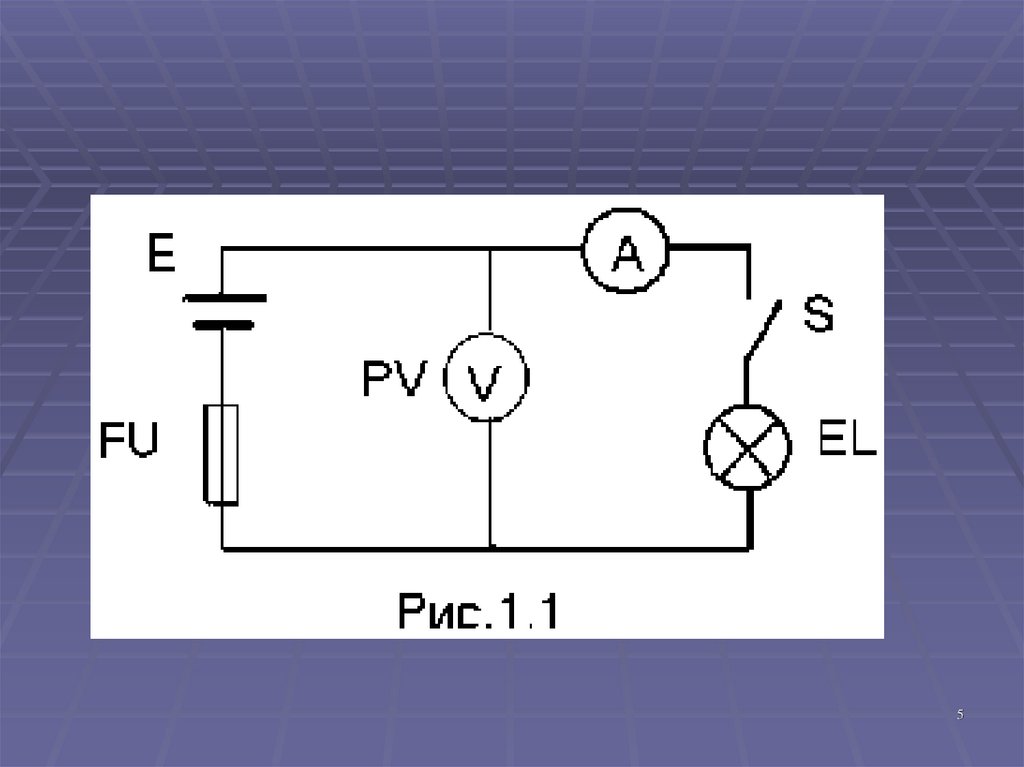
На рис 1.1 показана простейшая электрическая цепь постоянного тока,
состоящая из аккумуляторной батареи (источник), электрической
лампы (приемник), выключателя, контрольно-измерительной
аппаратуры (амперметр, вольтметр), элемента защиты
(предохранитель) и соединительных проводов
4

5.

5

6. Параметры элементов электрической цепи

Параметр сопротивления r характеризует свойство элемента
поглощать энергию из электрической цепи и преобразовывать ее в
другие виды энергий. Мощность (Р, р) преобразования электрической
энергии пропорциональна квадрату тока (I2, ί2), поэтому величина
этого параметра определяется отношением
r = P / I2 для постоянного тока и r = Р / i 2 для
переменного тока и измеряется в Омах (Ом).
Параметр индуктивности L характеризует свойство элемента цепи
создавать собственное магнитное поле (поле самоиндукции) при
протекании в нем тока. Он является коэффициентом
пропорциональности между током (I, i) и потокосцеплением ( , t )
данного устройства = L I или t = L i.
L является коэффициентом самоиндукции и измеряется в Генри (Г).
Емкостный параметр С характеризует свойство элемента
накапливать заряды или возбуждать ими электрическое поле. Этот
параметр является коэффициентом пропорциональности между
напряжением и зарядом элемента: q = C U,
q = C u.
В общем случае любое реальное устройство обладает всеми тремя
параметрами r, L, С. .
6

7. Схемы замещения электрических цепей

Графическое изображение цепи с помощью идеальных элементов,
параметрами которых являются параметры замещаемых элементов,
называют схемой замещения цепи
Для учета необратимого процесса поглощения энергии вводят
резистивный элемент. Индуктивные и емкостные элементы вводят в
схему замещения, когда хотят учесть влияние полей; катушку
индуктивности в цепи постоянного тока для учета ее нагрева
представляют только одним резистивным элементом. Но когда эту
катушку включают в цепь постоянного тока или отключают от нее и при
этом хотят установить законы изменения тока, ее уже представляют
двумя последовательно соединенными резистивным и индуктивным
элементами.
Все элементы цепи делятся на активные и пассивные.
Все источники электрической энергии являются активными элементами,
они характеризуются определенным значением э.д.с.
Приемники электрической энергии могут быть как пассивными, так и
активными. Пассивными называют приемники, в которых не возникает
э.д.с. Пассивный приемник, у которого сопротивление принимается
неизменным, называют пассивным линейным элементом электрической
цепи. Зависимость напряжения от тока в таком элементе U = r I.
7

8. Схемы замещения источников электрической энергии постоянного тока

Для источников электрической энергии известны значения Е и
внутреннего сопротивления rв. Однако у некоторых из них внутреннее
сопротивление настолько мало, что при определенных изменениях тока
напряжение остается практически неизменным, равным напряжению
холостого хода Uх, которое равно Е. Таким источником электрической
энергии соответствуют идеальные источники э.д.с. ВАХ (вольт –
амперная характеристика) идеального источника э.д.с. приведена на
рис.1.2.а, а его условное обозначение на рис.1.2.б. Поскольку
напряжение источника в этом является неизменным
(U = E), на схемах замещения часто показывают зажимы, к которым
приложено напряжение U.
8

9.

Идеальным источником тока называют источник, величина тока
которого не зависит от напряжения и равна току короткого замыкания
Iк источника питания. На рис.1.2.б,в приведены ВАХ источника тока
и его условное графическое обозначение.
Идеальные источники э.д.с. и тока являются источниками
бесконечной мощности, так как при увеличении в первом и
напряжения во втором источнике их мощности могут возрастать
теоретически до бесконечности.
9

10. Для реальных источников электрической энергии с э.д.с. Е, внутренним сопротивлением rв и током короткого замыкания Iк схемой

замещения с
источником э.д.с. называют схему, состоящую из последовательно
соединенных идеального источника э.д.с. и резистивного элемента,
сопротивление которого rв равно внутреннему сопротивлению источника
(рис.1.3.а).
Схемой замещения с источником тока называют схему, состоящую из
параллельно соединенных идеального источника тока и резистивного
элемента, сопротивление rв которого равно внутреннему сопротивлению
источника (рис1.3.б).
Внешняя характеристика реального источника ЭДС (рис1.4.а). может быть
записана уравнением
U = E - rв I
(1.1)
10

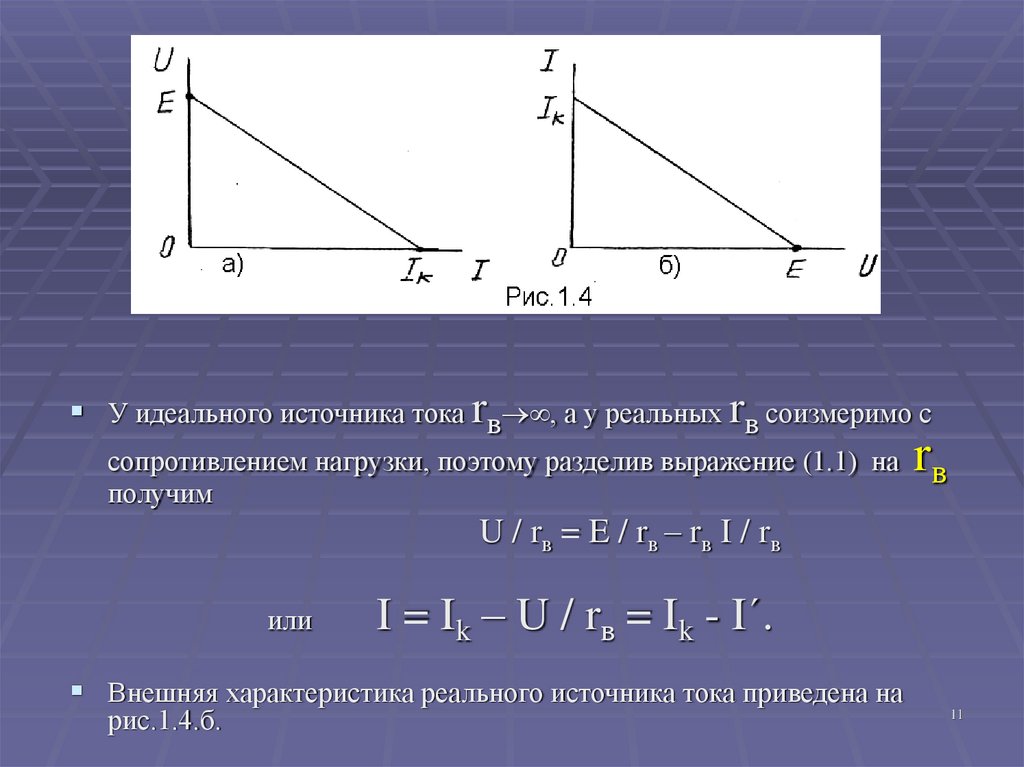
11.

У идеального источника тока rв , а у реальных rв соизмеримо с
сопротивлением нагрузки, поэтому разделив выражение (1.1) на
получим
rв
U / rв = E / rв – rв I / r в
или
I = Ik – U / rв = Ik - I´.
Внешняя характеристика реального источника тока приведена на
рис.1.4.б.
11

12. Топологические понятия теории электрических цепей

При расчете режима работы электрической цепи часто необходимо
определить токи, напряжения и мощности на всех ее участках при
заданных ЭДС источников и сопротивлениях участков цепи. Для
облегчения расчета составляется
схема замещения электрической цепи или просто электрическая схема.
На схеме изображают все элементы, влиянием которых на результат
расчета пренебречь нельзя.
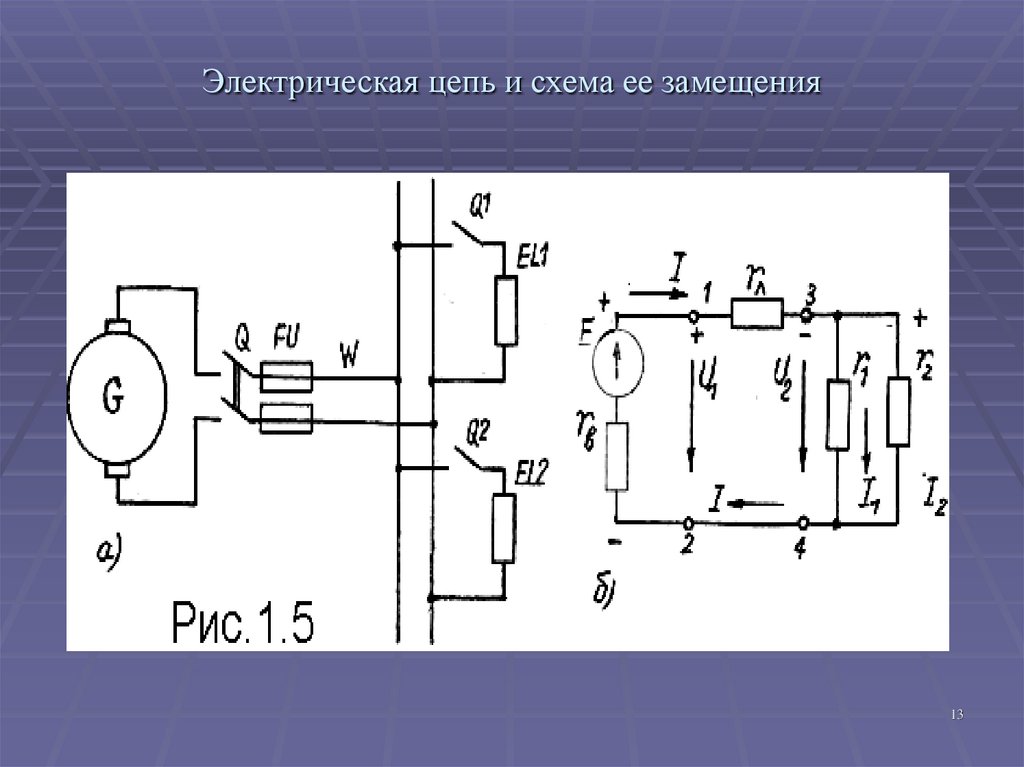
На рис.1.5. приведена электрическая цепь и схема ее замещения.
В этой схеме генератор G электрической энергии представлен ЭДС Е и
внутренним сопротивлением rВ, сопротивление проводов линии W
заменено сосредоточенным сопротивлением rл,
два приемника EL1 и EL2 заменены сопротивлениями r1 и r2.
12

13. Электрическая цепь и схема ее замещения

13

14.

Ветвью электрической цепи называется ее участок, состоящий из
одного или нескольких элементов, соединенных так, что по ним
проходит один и тот же ток. Например, ветвь, состоящая из источника
питания с ЭДС Е и внутренним сопротивлением rв и резистора с
сопротивлением rл показана на рис.1.5.б. На этом же рисунке ветвями
являются цепи с сопротивлением r1 и r2. Таким образом на схеме
рис.1.5.б. изображено три ветви.
Точка электрической цепи называется узлом (точкой
разветвления), если в ней соединены три или большее число ветвей
или проводов на схеме замещения (рис.1.5.б) согласно определению,
два узла в точках 3 и 4. В узле 3 соединены три ветви с токами I, I1,
I2 и в узле 4 с такими же токами.
Контур электрической цепи представляет собой замкнутый путь,
проходящий по нескольким ветвям. В схеме рис.1.5.б можно выделить
три контура.
14

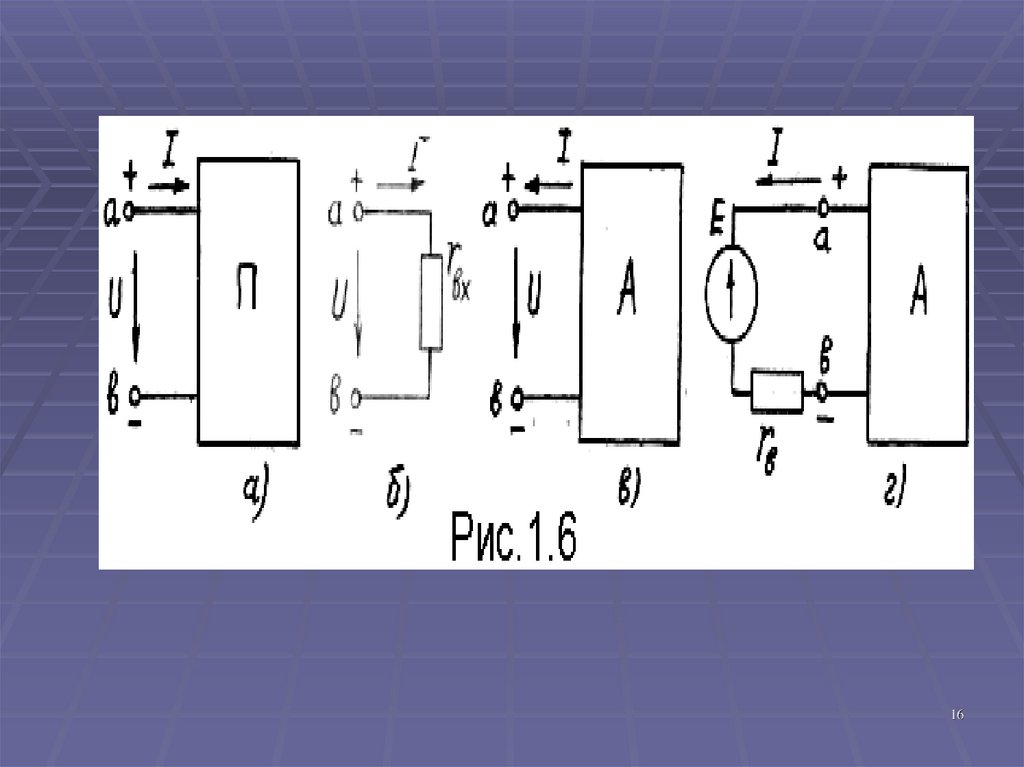
15. Часть электрической цепи с двумя внешними выводами (полюсами), которыми она может быть присоединена к другим ветвям или

участкам называется двухполюсником.
Двухполюсник, не содержащий источников питания,
называется пассивным, а содержащий источник питания –
активным.
У пассивного двухполюсника, обозначение которого
показано на рис.1.6.а одинаковое направление напряжения и
тока относительно выводов а и в.
Отношение U / I = rвх = rв называют входным или внутренним
сопротивлением пассивного двухполюсника. Если при
заданном напряжении U заменить двухполюсник его
входным сопротивлением (рис.1.6.б), то не изменится ток I.
И наоборот, при
заданном токе I не изменится напряжение U.
15

16.

16

17. Активным двухполюсником является любая часть электрической цепи с двумя выводами (а и в), к которым могут быть присоединены

другие участки цепи, если она
содержит источник питания (рис.1.6.в).
Активный двухполюсник можно заменить источником с ЭДС
равной напряжению холостого хода E = Uх и внутренним
сопротивлением rв = Uх / Ik (или источником тока рис.1.6.г.)
Электрические цепи по способу соединения элементов
подразделяются на неразветвленные и разветвленные.
В неразветвленной электрической цепи все элементы цепи
соединены между собой последовательно. Отличительной
особенностью такого соединения является то, что
электрический ток во всех участках один и тот же.
В разветвленной электрической цепи можно выделить
участки с последовательным и параллельным соединением
элементов.
17

18. Положительные направления токов, ЭДС и напряжений Для однозначности описания процессов необходимо знать не только величины его

тока, но направления в
рассматриваемый момент времени. Стрелки, поставленные
на схемах, указывают положительные направления.
За положительное направление тока принято направление
движения положительных зарядов.
За положительное движение ЭДС – направление действия
сторонних сил на положительный заряд, за положительное
направление напряжения – направление убывания
потенциала.
Так как положительные заряды внутри источника движутся в
направлении действия сторонних сил, а в приемнике – в
направлении убывания потенциала, то положительные
направления тока и ЭДС источника и напряжения приемника
совпадают (рис.1.5.б).
18

19. Режимы работы электрической цепи

Любую сложную электрическую цепь можно представить в виде активного
двухполюсника, соединенного с пассивным двухполюсником рис 1.7.
Работа активного двухполюсника, подключенного к пассивному двухполюснику,
характеризуется режимами: холостого хода, короткого замыкания,
согласованным и номинальным режимами
Режим холостого хода соответствует отсутствию тока в приемнике и
осуществляется отключением пассивного двухполюсника от активного.
Напряжение холостого хода активного двухполюсника Uх = Е. Так как ток
отсутствует, то потери напряжения и мощности в элементах цепи равны нулю.
В этом случае коэффициент полезного действия источника равен единице.
Режим короткого замыкания возникает тогда, когда сопротивление
приемника равно нулю. При этом напряжение на зажимах активного
двухполюсника также равно нулю, т.е. Uк = 0. Ток в этом случае достигает
максимального значения, он ограничен лишь внутренним сопротивлением
активного двухполюсника Iк = Е / rв. Такой режим является аварийным, так
как возникающие при этом токи во много раз превышают номинальные
значения, на которые рассчитаны элементы цепи. К.п.д. источника равно
нулю ( = 0).
19

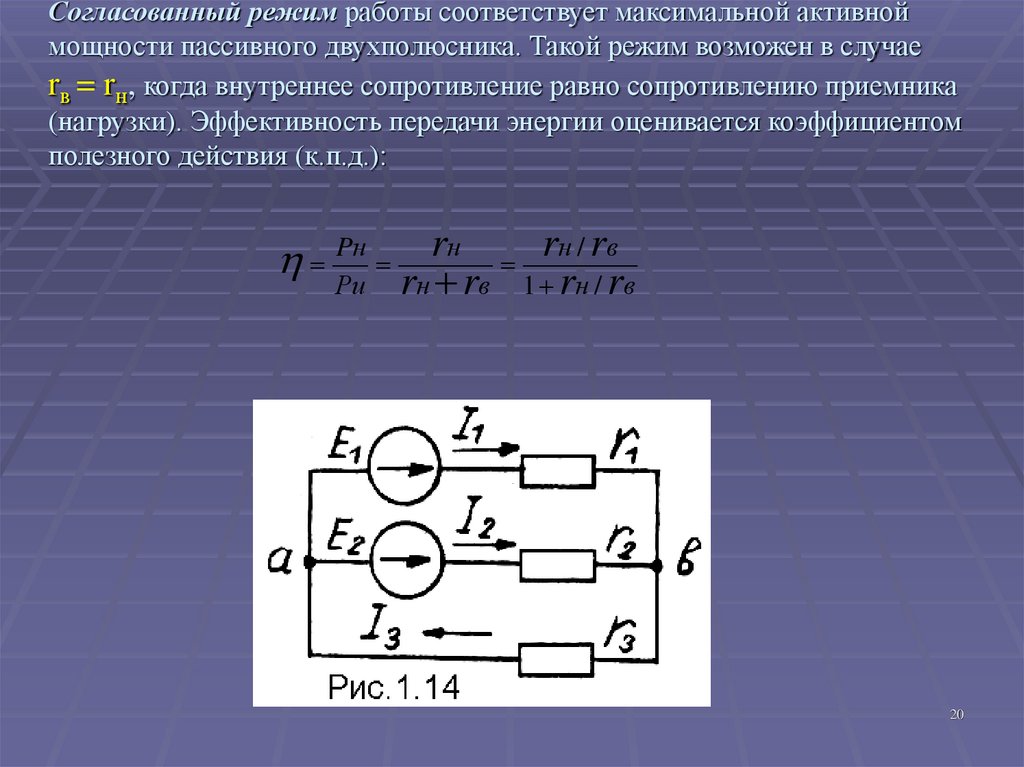
20. Согласованный режим работы соответствует максимальной активной мощности пассивного двухполюсника. Такой режим возможен в случае

rв = rн, когда внутреннее сопротивление равно сопротивлению приемника
(нагрузки). Эффективность передачи энергии оценивается коэффициентом
полезного действия (к.п.д.):
Pн
rн rн / rв
Ри
rн rв 1 rн / rв
20

21. Номинальный режим соответствует режиму источников и приемников электрической энергии при тех значениях токов и напряжений, на

которые они рассчитаны заводами – изготовителями. Номинальные
значения токов и напряжений и мощностей указываются в каталогах и
паспортах для всех источников и приемников электрической энергии.
Чаще всего номинальный режим работы соответствует случаю, когда
сопротивление приемника много больше внутреннего сопротивления
источника. При этом близок к единице, что очень важно для силовых
электротехнических устройств и установок.
21

22. Законы Кирхгофа

Первый закон Кирхгофа относится к узлам электрической цепи
Первый закон Кирхгофа отражает принцип непрерывности движения
электрических зарядов, т.е. все заряды,
притекающие в любой узел электрической
цепи, из него вытекают.
Поэтому исходя из баланса токов в узле: первый закон Кирхгофа в
общем виде:
k
I 0
i 1
K
где к - число ветвей сходящихся в узле.
В этой сумме токи берутся с различными знаками в зависимости
от направления их по отношению к узлу. Укажем на рис.1.14
направление токов в ветвях цепи. За положительное направление
токов принимается направление действия сторонних сил на
заряженные частицы. Поэтому на схеме токи I1 и I2 совпадают со
своими ЭДС. В соответствии с этим первый закон Кирхгофа может
быть записан таким образом:
I1 + I2 = I 3 .
22

23. Второй закон Кирхгофа

Применяется к контурам электрической цепи и является следствием
закона сохранения энергии. Согласно этому закону в любом
замкнутом электрическом контуре алгебраическая сумма ЭДС равна
алгебраической сумме падения напряжений на элементах схемы,
входящих в этот контур.
к m
k n
Е r I
i 1
K
i 1
k
K
Условимся, что положительные напряжения соответствуют направлению
обхода контура как и ЭДС источника.
Применение второго закона Кирхгофа необходимо при анализе
большинства электрических схем, содержащих два и более источника
электроэнергии
23

24. Лекция №2 Эквивалентные преобразования пассивных участков электрических цепей

Последовательное соединение элементов цепи
rэкв = r1 + r2 + r3
U / I = rэкв
K
r
i 1
K
24

25.

Параллельное соединение элементов цепи
rэкв = r / n
25

26.

Смешанное соединение
r12 = r1 + r2,
r34 = r3 r4 / (r3 +r4)
26

27. Анализ электрического состояния разветвленных электрических цепей с несколькими источниками электрической энергии

Сложная цепь – это цепь содержащая два и более активных элемента со
смешанным соединением пассивных элементов.
Метод узлового напряжения
Суть метода заключается в определении
узлового напряжения Uав
I1 + I2 + I3 = 0
Е1 – Uав = r1I1,
Е2 - Uав = = r2 I2,
- Uав = r3 I3.
I1 = (E1 - Uав) g1,
I2 = (E2 - Uав) g2 ,
I3 = -Uав*g3
27

28.

Метод контурных токов
Для расчета цепи методом непосредственного использования первого и второго
законов Кирхгофа необходимо решать систему уравнений, равную числу токов
при известных параметрах источников и элементов схемы.
I контур
II контур
E1 – E2 = II (r1 + r2) – III r2,
E2 = III (r2 + r3) – II r2.
28

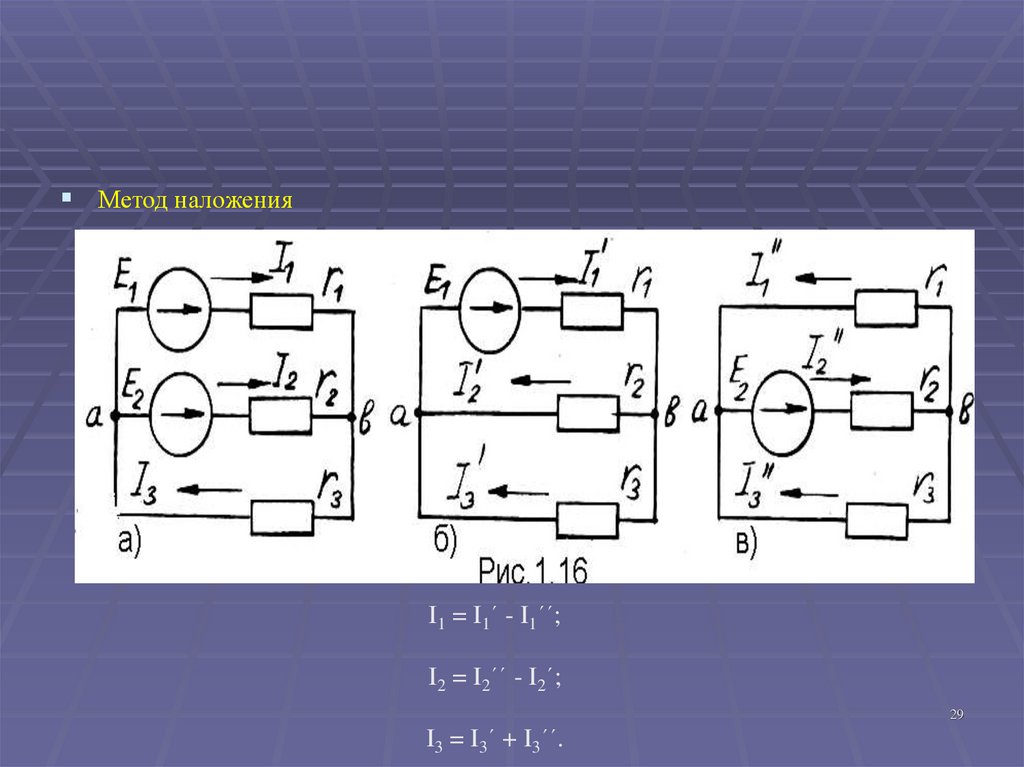
29.

Метод наложения
I1 = I1´ - I1´´;
I2 = I2´´ - I2´;
29
I3 = I3´ + I3´´.

30. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Нелинейной называется электрическая цепь, в которую входит хотя бы один
нелинейный элемент.
Нелинейный элемент – это такой элемент, сопротивление которого зависит от
тока в нем и от напряжения на его зажимах.
К линейным элементам относятся электротехнические устройства, у которых
токоведущие детали выполнены из манганина или константана.
30

31. Лекция №3 Линейные электрические цепи однофазного переменного тока

Получение синусоидальных значений ЭДС, напряжения и тока.
Переменным током (ЭДС) в электрических цепях называется такой ток (ЭДС),
которые изменяют свое значение и направление со временем.
В электротехнике в основном приходится иметь дело с
которого изменяется по синусоидальному закону.
е = B ℓ υ sin α
током, величина
Характеристики синусоидальных величин
Синусоидально изменяющиеся ЭДС, напряжения и ток характеризуются
следующими величинами:
- мгновенным значением,
- периодом,
- частотой,
- фазой (сдвигом фаз) рис.2.1.
31

32.

Мгновенное значение ЭДС, напряжения и тока - значение этих величин в любой
момент времени. Мгновенные значения обозначаются строчными буквами е, u,
ί.
Амплитуда - это наибольшие значения, которые принимают ЭДС, напряжение и
ток. Она является наибольшим значением этих величин. Амплитудные значения
обозначаются прописными буквами Еm, Um , Im .
Период Т - промежуток времени в течение которого ЭДС, напряжение и ток
совершают полное колебание и принимают прежнее по величине и знаку
значение.
Частота ƒ (число периодов в секунду) - величина обратная периоду
ƒ=1/Т
32

33.

Действующее и среднее значение переменного тока
Действующим значением переменного тока называется постоянный ток, который
за время одного периода оказывает такое тепловое (механическое и др.) действие,
как и данный переменный ток
Из этого уравнения получают действующее
значение тока:
33

34.

Если
следовательно,
Соотношения действующего значения переменного тока справедливы и для ЭДС,
напряжения и магнитного потока
34

35. Лекция №4 Идеальные элементы цепи переменного тока. Схемы замещения

По сравнению с цепями постоянного тока цепи переменного тока имеют ряд
особенностей.
Рассматривая процессы происходящие в лампе накаливания, включенной в цепь
переменного тока, отметим, что между отдельными витками спирали существует
емкость, а сама спираль обладает определенной индуктивностью. Однако на
промышленной частоте токи смещения, существующие в диэлектрике между
витками, значительно меньше тока проводимости, поэтому ими можно
пренебречь. ЭДС самоиндукции, возникающая в спирали, составляет доли
процента от напряжения, приложенного к лампе, поэтому ею тоже можно
пренебречь.
Если принять:
(С = 0,
L = 0)
то лампа характеризуется только необратимым процессом преобразования
электрической энергии в тепловую и лучистую. Поэтому электрическую лампу
называют идеальным резистивным элементом.
35

36.

К идеальным резистивным элементам относят: реостаты, большинство
электронагревательных устройств, резисторы.
Индуктивный элемент схемы замещения с изменяющимся то-ком характеризует
наличие изменяющегося магнитного поля, созданного этим током.
Идеальная катушка - это такая катушка, в которой токи смещения между
витками несоизмеримо малы по сравнению с токами проводимости (С = 0) и
катушка практически не нагревается (r = 0).
Под действием переменного тока в катушке возникает ЭДС самоиндукции. ЭДС
самоиндукции противодействует изменению тока, обуславливая индуктивное
сопротивление катушки. За счет ЭДС самоиндукции происходит возврат энергии
магнитного поля катушки в электрическую цепь. В результате источник и катушка
обмениваются энергией.
Индуктивное сопротивление является реактивным сопротивлением.
При постоянном токе индуктивное сопротивление равно нулю, так как ЭДС
самоиндукции не возникает.
Емкостный элемент вводится в схему замещения с изменяющимся током, когда
хотят учесть влияние изменяющегося электрического поля элементов цепи.
36

37.

В конденсаторе, подключенном к источнику переменного на-пряжения,
изменяется заряд q = Cu,
и в элементах цепи между источником и конденсатором проходит переменный
ток.
Когда конденсатор полностью заряжается
(u = Um)
энергия электрического поля конденсатора
Wс = C·U2/2
максимальна. Основываясь на законе электромагнитной индукции току в цепи
оказывает противодействие напряжение конденсатора, обуславливающее
емкостное сопротивление хс.
Ввиду обмена энергией между источником и конденсатором емкостное
сопротивление является реактивным.
37

38.

Изображение синусоидальных величин синусоидамии вращающимся
вектором
При расчете электрических цепей переменного тока пользуются
простым и наглядным способом графического изображения синусоидальных
величин при помощи вращающихся векторов.
Пусть напряжение задано уравнением
u = Um sin (ωt + ψ).
Проведем две перпендикулярные оси. Из точки пересечения осей проведем вектор
длиной Um в выбранном масштабе (рис. 2.4). Направление вектора выбирается таким,
чтобы с горизонтальной осью он составлял угол ψ, т.е. равным начальной фазе. Проекция
этого вектора на ось ординат определяет мгновенные значения напряжения
38
u(0) = Um sin ψ

39.

При построении векторов положительные углы отсчитываются от
горизонтальной оси против вращения часовой стрелки, а отрицательные по
часовой стрелке.
Совокупность векторов, изображающих на одном чертеже несколько
синусоидальных величин одинаковой частоты в начальный момент времени,
называется векторной диаграммой.
39

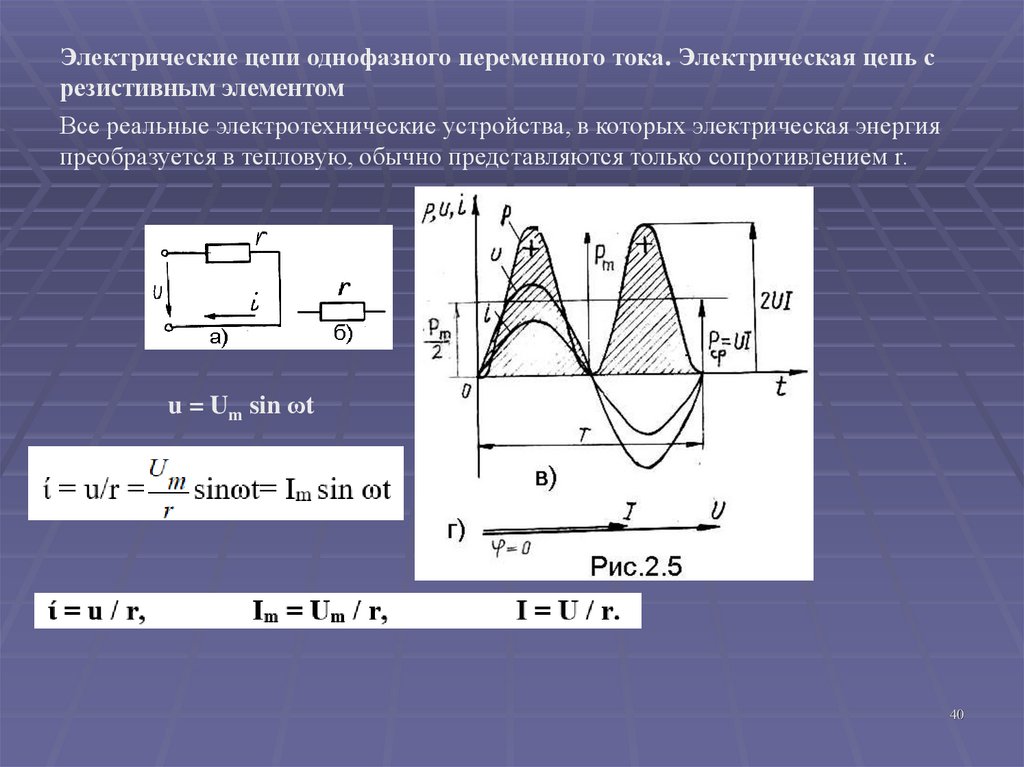
40.

Электрические цепи однофазного переменного тока. Электрическая цепь с
резистивным элементом
Все реальные электротехнические устройства, в которых электрическая энергия
преобразуется в тепловую, обычно представляются только сопротивлением r.
u = Um sin ωt
40

41.

Мгновенное значение мощности равно произведению мгновенных значений тока
и напряжения р = u ί.
Таким образом, мгновенная мощность в любой момент времени состоит из
постоянной мощности (U I) и переменной мощности
(U·I cos 2ωt).
Так как cos 2ωt может изменяться от +1 до -1, то мгновенная мощность изменяется от
0 до (2 UI), т.е. будет пульсировать.
Постоянство знака мощности указывает на то, что направление потока мощности за
период неизменно. Электрическая энергия в этом случае передается от источника к
приемнику.
За период вторая составляющая мгновенной мощности равна нулю и получим Р = U I,
которая от времени не зависит. Эта мощность равна средней мощности за период и
называется активной мощностью Р:
41

42.

Цепь с индуктивностью
Векторная диаграмма
На (рис.2.6, а) приведена
схема электрической цепи с
катушкой
индуктивности.
Условное
обозначение
индуктивности приведено на
(рис. 2.6, б).
При прохождении по катушке переменного тока
ί = Im sin ωt
в ней будет возбуждаться ЭДС самоиндукции
е = - L dί /dt,
значение которой пропорционально скорости изменения тока (dί /dt).
В момент времени t = 1/4 Т скорость изменения тока равна нулю (dί/dt = 0), равна
нулю и ЭДС самоиндукции.
42

43.

Из графиков синусоид тока ί и еL видно, что ЭДС самоиндукции отстает по
фазе от тока в катушке на угол π /2.
По закону Ленца ЭДС самоиндукции еL имеет противоположное направление
подведенному к катушке напряжению uL, которое уравновешивает ЭДС
самоиндукции еL , т.е. находится в противофазе с еL и на графике представлено
синусоидой uL .
закон Ома для участка цепи с индуктивностью.
L играет роль индуктивного сопротивления: хL = ωL.
При передаче электроэнергии от источника к приемнику принять считать мощность
положительной, а наоборот отрицательной
Мера обмена энергией за единицу времени между источником и индуктивной
катушкой, затрачиваемой на создание магнитного поля, называется реактивной
мощностью и обозначается QL
QL = UL I = хL I2
Единицу мощности называют вар - вольт-ампер реактивный.
43

44.

Цепь с емкостью
ёмкостное сопротивление
Для получения хc в омах нужно емкость выражать в фарадах. Емкостное
сопротивление обратно пропорционально частоте тока и емкости конденсатора
(цепи).
Напряжение отстает от тока по фазе на 90o
44

45. Лекция №5 Цепь с реальной катушкой индуктивности

Реальная катушка должна быть представлена активным и реактивным элементом.
Такое деление катушки на два элемента искусственно, однако представив реальную
катушку из двух не совмещенных элементов, один из которых характеризуется r, а
другой хL дает возможность объяснить довольно сложный процесс.
dI
e L
dt
i (U L dI )
dt
i Imsin t
U Im r sin t Im I cos t Im r sin t Im I sin( t 900 )
45

46.

Первое слагаемое ur это падение напряжения на резисторе, а второе - на
идеальной катушке uL, в которой напряжение опережает ток на 90о. Величины ur
и uL по фазе не совпадают.
Согласно второму закону Кирхгофа U U U
r L
где Ur = I·r,
UL = хL∙ I для действующих значений и Urm = Im r, ULm = хLI для амплитудных
значений.
Uа = Ur
Uа = U cos φ
Реактивная составляющая вектора
напряжения UL = U sin φ
46

47.

Таким образом, если ток имеет начальную фазу равную нулю, то напряжение на
реальной катушке опережает ток на угол φ, что следует из векторной
диаграммы u = Um sin (ωt + φ).
Разделим стороны прямоугольного треугольника на ток I и в результате получим
треугольник сопротивлений (рис. 2.9, б), катетами которого являются активное
сопротивление r U / I и индуктивное сопротивление
r
z U / I
X L U L / I
Гипотенузой является величина
, называемая полным
сопротивлением.
Из треугольника сопротивлений следует, что модуль сопротивления равен
z=
r 2 хL2
Закон Ома в таком случае:
47

48.

Пример 1. В цепи содержащей последовательно соединенные r = 30 Ом и L =
0,127 Гн, приложено синусоидальное напряжение u = 141 sin ωt, частота
которого 50 Гц. Найти ток, падение напряжения на участках цепи и угол сдвига
фазы между напряжением и током.
Решение. Находим индуктивное сопротивление
хL = ωL = 2 πƒ L = 2 π 50·0,127 = 40 Ом
Полное сопротивление цепи
Действующее напряжение в цепи
Ток в цепи I = U / z = 100 / 50 = 2 А.
Падение напряжения на элементах схемы Ur = r I = 30·2 = 60 В,
40·2 = 80 В
Угол сдвига фазы между напряжением и током
φ = arctg xL / r = arctg 40/30 = 53o .
UL = x L I =
48

49. Последовательное соединение активного, индуктивного и емкостного сопротивлений

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ
АКТИВНОГО, ИНДУКТИВНОГО И
ЕМКОСТНОГО СОПРОТИВЛЕНИЙ
В цепи (рис. 2.10) под действием разности потенциалов U течет ток I, создавая
падение напряжения на элементах схемы r, L, С.
В соответствии со вторым законом Кирхгофа
U U r U L U c
при последовательном соединении элементов по ним протекает одинаковый ток,
тогда
Ur Ir
UL X LI
Uc X c I
49

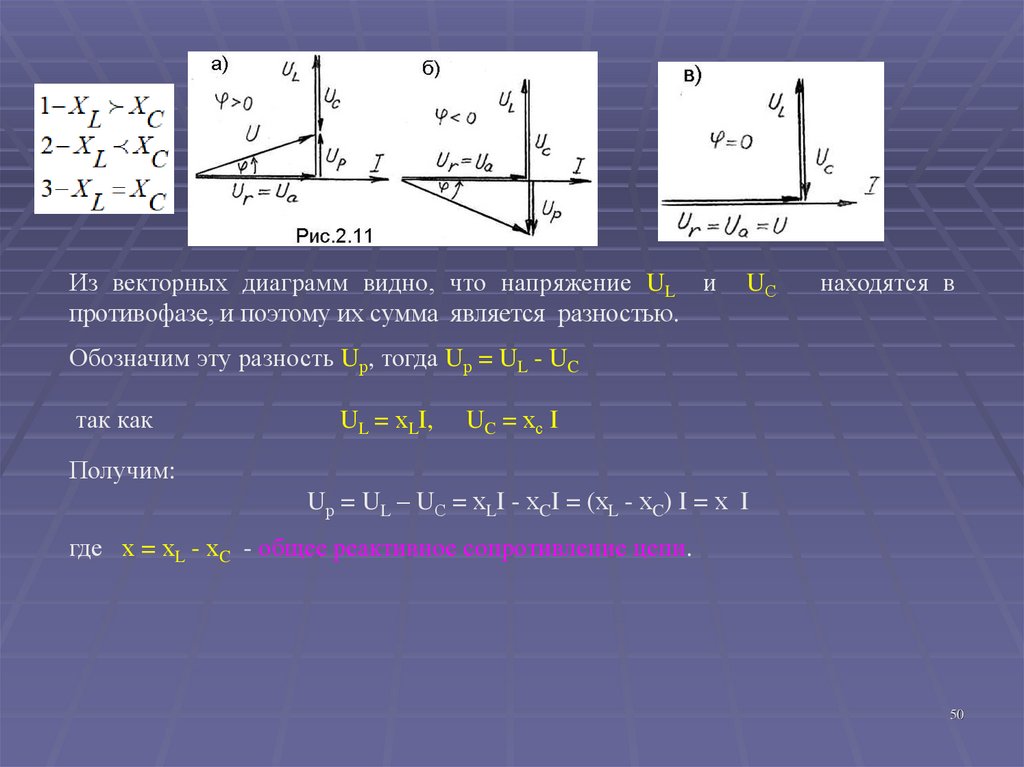
50.

Из векторных диаграмм видно, что напряжение UL и
противофазе, и поэтому их сумма является разностью.
UС
находятся в
Обозначим эту разность Uр, тогда Uр = UL - UC
так как
UL = хLI,
UC = хс I
Получим:
Uр = UL – UС = хLI - хCI = (хL - хC) I = х I
где х = хL - хC - общее реактивное сопротивление цепи.
50

51.

Полное сопротивление цепи
является коэффициентом пропорциональности между действующим значением тока
и общего напряжения цепи:
Из треугольников напряжений и сопротивлений определяются величины:
51

52.

В случае в (рис. 2.11) угол сдвига фаз между током и общим напряжением равен
нулю, так как
Ua U
тогда
U Ir
U U U 0
P
L C
в этом случае при равенстве
в цепи имеет место резонанс напряжений
Построенные в случаях а и б (рис. 2.11) векторные диаграммы дают основания
считать, что мы имеем треугольники напряжений, катеты составляют активную и
реактивную составляющие, а гипотенуза - полное напряжение. Разделив стороны
треугольника на общий ток, получим треугольник сопротивлений, в котором катеты
составят активное и реактивное сопротивления, а гипотенуза - полное.
Если стороны треугольника напряжений умножить на один и тот же ток, получим
треугольник мощностей (рис. 2.12).
52

53. РЕЗОНАНС НАПРЯЖЕНИЙ

Если подключить цепь с последовательным соединением резистора, катушки
индуктивности и конденсатора в сеть переменного тока, то в цепи могут
возникнуть электрические колебания. При малом активном сопротивлении и
равенстве угловых частот возникнет резкое увеличение амплитуды колебания
тока - электрический резонанс.
или
т.е.
или
53

54.

В режиме резонанса полное сопротивление цепи принимает минимальное
значение и является активным
Ток в цепи в режиме резонанса принимает максимальное значение
Напряжение на индуктивности и емкости во столько раз больше подведенного
напряжения, во сколько раз реактивное сопротивление больше активного
сопротивления цепи.
54

55.

Из соотношения ωL = 1/ωC, выражающего условие резонанса, видно, что резонанса
можно добиться двумя путями:
1)изменением частоты подведенного напряжения при постоянных значениях L и С;
2)изменением L или С при неизменной частоте питающего напряжения.
55

56. ПАРАЛЛЕЛЬНОЕ СОДИНЕНИЕ АКТИВНОГО, ИНДУКТИВНОГО И ЁМКОСТНОГО СОПРОТИВЛЕНИЙ

Рассмотрим аналитический метод расчета разветвленных цепей. Этот метод
заключается в следующем, вектора токов каждой ветви проецируют на направление
вектора напряжения и на направление перпендикулярное к нему и определяет
активную и реактивную составляющие токов каждой ветви. Тогда модуль общего
тока в неразветвленной части цепи равен:
56

57.

Проводимостью цепи называется величина, обратная сопротивлению.
Общая проводимость разветвленной цепи равна Y=1/Z,
активная проводимость g = 1/r.
57

58. АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТЬ

58

59. РЕЗОНАНС ТОКОВ

Резонанс токов возникает в электрических цепях при параллельном соединении
индуктивной и емкостной проводимости ветвей bL = bС .
Величина тока при резонансе в неразветвленной части цепи минимальная и
только активная. Сдвиг фаз между током и напряжением равен нулю,
При резонансе токов
отсюда резонансная частота
Резонанс токов можно получить изменением параметров L и C или изменением
частоты источника энергии.
59

60. Технико-экономическое значение реактивной мощности в электрических системах

В сети, имеющей активное сопротивление R, при передаче активной мощности Р
и реактивной Q через элемент сети потери активной мощности составят:
Дополнительные потери активной мощности ΔРр, вызванные протеканием
реактивной мощности Q, пропорциональны ее квадрату. Возросшая полная
передаваемая мощность обуславливает появление дополнительных потерь
напряжения в сетях с активным и реактивным напряжениями.
Где ΔUа, ΔUр - потери напряжения, обусловленные активной и
реактивной мощностью.
60

61.

Дополнительные потери напряжения ΔUр увеличивают отклонения напряжения на
зажимах приемника от номинального значения при изменениях нагрузок и режимов
электрической сети. Это требует увеличения мощности, а следовательно, и
стоимости средств регулирования напряжения. Учитывая, что коэффициент
мощности
Если R заменить через ℓ / γ S получим
откуда сечение провода
т.е. при той же допустимой потере мощности сечение проводов обратно
пропорционально квадрату коэффициента мощности.
61

62. ИСПОЛЬЗОВАНИЕ КОНДЕНСАТОРОВ ДЛЯ КОМПЕНСАЦИИ РЕАКТИВНОЙ МОЩНОСТИ

Уменьшение реактивной мощности, циркулирующей между источником тока и
приемником, а следовательно, и уменьшение реактивного тока в генераторах и
сетях называется компенсацией реактивной мощности.
Если необходима частичная компенсация сдвига фаз, то емкостной ток
откуда емкость компенсирующего устройства (конденсатора),
где Р - активная мощность нагрузки, Вт.
62

63. Лекция №6 ТРЁХФАЗНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ Принцип получения трёхфазной ЭДС. Соединение обмоток генератора

Каждую из однородных цепей, входящих в трехфазную цепь, называют фазой.
63

64.

В генераторах обмотка переменного тока неподвижна (расположена на статоре), а
магнитные полюса вращаются (расположены на роторе). При вращении ротора в
обмотках индуцируются ЭДС с одинаковыми амплитудами, сдвинутые по фазе, друг
относительно друга на 120°. Такая система ЭДС называется симметричной.
Согласно (рис. 1), при вращении ротора по часовой стрелке,
уравнения ЭДС в фазах можно записать в таком виде (тригонометрическая форма
представления трехфазных величин):
Этим уравнениям соответствуют графики ЭДС, изображенные на
рисунке 2 (графическая форма представления трехфазных величин).
64

65.

Кроме тригонометрической и графической формы изображения трехфазных величин
используется и векторная форма в виде трех векторов, равных по величине и
сдвинутых друг относительно друга на угол 1200, представляющих собой
трехлучевую звезду (рис. 3).
Геометрическая сумма действующих значений ЭДС трехфазного генератора равна
нулю, так как сумма векторов ЕА и ЕВ дает вектор, равный ЕС, сдвинутый по фазе
относительно его на 1800:
Алгебраическая сумма мгновенных значений ЭДС также равна нулю. Например, для
момента времени t = Т/4 получим:
65

66.

Следовательно,
Если поменять местами какие-либо два вектора, в реальных условиях это
равнозначно
изменению
направления
вращения
ротора
генератора,
последовательность фаз при этом изменится, и будет называться обратной. Обычно
на практике применяется прямая последовательность фаз.
Условное изображение обмотки генератора (источника) показано на рисунке 4.
За условное положительное направление ЭДС в
каждой фазе принимают направление от конца к
началу. Начала обмоток статора генератора
маркируются А, В, С, концы - X, Y, Z.
66

67. СПОСОБЫ СОЕДИНЕНИЯ ФАЗ ТРЕХФАЗНОГО ИСТОЧНИКА ПИТАНИЯ

К каждой фазе генератора подключается нагрузка. Если фазы обмотки
электрически не соединены между собой, то они образуют не связанную
трехфазную систему цепей. Значит, каждая из фаз соединяется со своим
приемником парой проводов. Такая система неэкономична, так как имеет большое
число проводов, соединяющих источник и приемник. Более экономичны связанные
цепи, в которых фазы обмотки соединены между собой.
Разработал и внедрил в практику связанные трехфазные цепи с соединением фаз в
звезду и треугольник в начале 90-х годов XIX века М.О.Доливо-Добровольский.
67

68.

При соединении фаз обмотки генератора звездой (рис. 5, а) их концы X, Y, Z
соединяют в общую точку N, называемую нейтральной точкой. Провод,
присоединяемый к этой точке, называют нейтральным проводом.
К началам фаз, обозначаемым А, В и С присоединяют провода,
соединяющие источник с приемником, и называют их линейными.
При соединении фаз источника звездой трехфазная цепь может быть
трехпроводной и четырехпроводной. В трехпроводной цепи нейтральные точки
источника и приемника не соединяются проводом, а в четырехпроходной
соединяются.
При соединении фаз источника треугольником соединяются начала и концы
фаз: конец первой фазы с началом второй, конец второй с началом третьей, конец
третьей с началом первой, X-В, Y-С,
Z-А (рис. 5, б), т.е. фазные обмотки
соединяются последовательно. Это вовсе не является опасным, если ЭДС изменяются
синусоидально, так как в симметричной системе сумма ЭДС фаз равна нулю,
Напряжение, измеренное между началом и концом фазы, или между
линейным и нейтральным проводом, называется фазным напряжением Uф.
Таким образом имеется три фазных напряжения: UА, UВ, UС.
Напряжение, измеренное между линейными проводами, или началами фаз
называется линейным Uл. Следовательно, имеем три линейных напряжения UАВ, UВС,
UСА.
68

69.

Положительное направления тока в фазах совпадает с положительным
направлением ЭДС, а положительное направление напряжения на фазе приемника
совпадает с направлением тока, т.е. от начала фазы к ее концу. Напряжение на фазе
генератора будет иметь такое же направление, как и на фазе приемника, т.е.
противоположное положительному направлению ЭДС.
При симметричной нагрузке фаз генератора векторная диаграмма
напряжений, как и векторная диаграмма ЭДС, также представляется трехлучевой
симметричной звездой и геометрическая сумма напряжений
Пренебрегая падением напряжения в обмотках генератора, можно считать фазные
напряжения равными ЭДС и при нагрузке генератора.
Тогда
При соединении фаз генератора звездой выполняется соотношение:
69

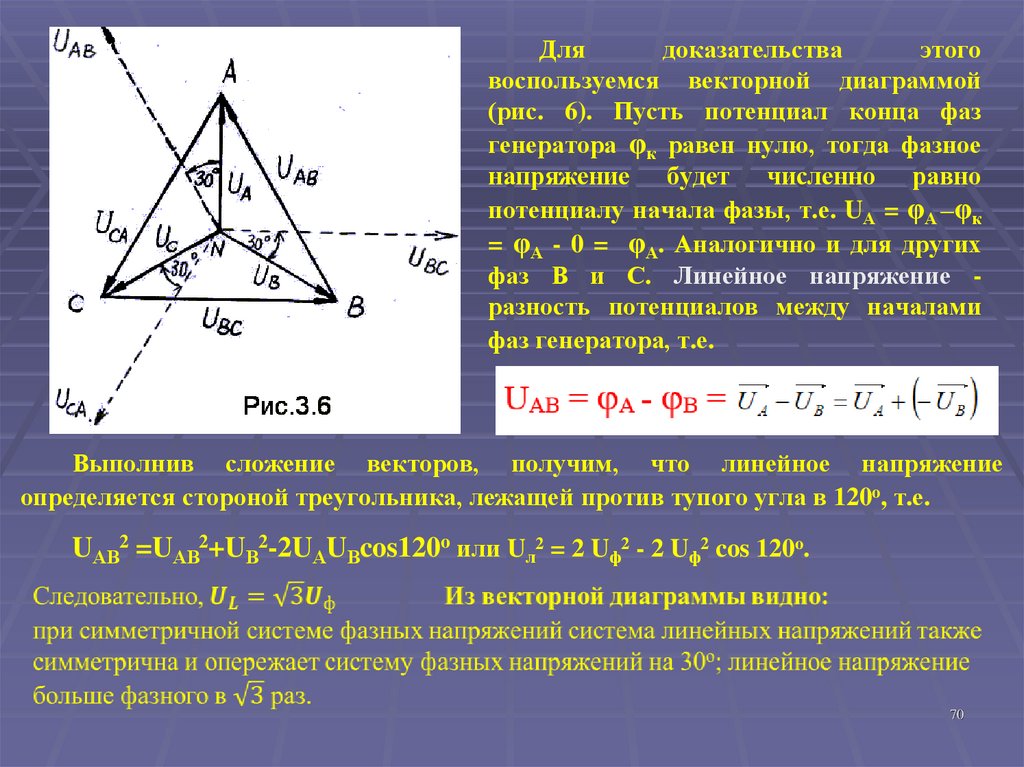
70.

Для
доказательства
этого
воспользуемся векторной диаграммой
(рис. 6). Пусть потенциал конца фаз
генератора φк равен нулю, тогда фазное
напряжение будет численно равно
потенциалу начала фазы, т.е. UА = φА –φк
= φА - 0 = φА. Аналогично и для других
фаз В и С. Линейное напряжение разность потенциалов между началами
фаз генератора, т.е.
Выполнив сложение векторов, получим, что линейное напряжение
определяется стороной треугольника, лежащей против тупого угла в 120o, т.е.
UАВ2 =UАВ2+UВ2-2UАUВcos120o или Uл2 = 2 Uф2 - 2 Uф2 cos 120o.
70

71. СОЕДИНЕНИЕ ЭЛЕКТРОПРИЕМНИКОВ ЗВЕЗДОЙ. СИММЕТРИЧНЫЙ РЕЖИМ

На (рис. 7) приведена схема
соединения фаз источника и
приемника звездой.
Если от генератора отводят только
три провода - А, В, С, то такую
систему называют трехфазной
трехпроводной. Если отводят
также четвертый, нейтральный,
провод N, то систему называют
трехфазной четырехпроводной.
Приемники
заданы
полным
сопротивлением zа, zв, zс.
При равенстве zа = zв = zс цепь
считается симметричной,
при неравенстве сопротивлений zа
≠ zв ≠ zс - несимметричной.
71

72.

При симметричной нагрузке можно использовать трехфазную трехпроводную схему
соединения звездой, т.е. в трехфазную трехпроводную цепь соединением звездой
включаются только симметричные приемники.
При активной нагрузке токи совпадают по фазе с напряжением. В большинстве
случаев нагрузка активно-индуктивная, и между напряжением и током имеется сдвиг
фаз на угол φ. Такому случаю соответствует векторная диаграмма изображенная на
рис. 8.
При симметричной нагрузке необходимость расчета всех трех фаз отпадает.
Достаточно произвести расчет одной фазы. При известном линейном
напряжении Uл фазное напряжение равно:
Фазный ток равен линейному:
72

73. Лекция №7 НЕСИММЕТРИЧНЫЙ РЕЖИМ

Нейтральный провод обеспечивает симметрию
приемника при несимметричной нагрузке.
фазных
напряжений
Ток в нейтральном проводе:
Если сопротивление нейтрального провода не равно нулю, zN ≠ 0, то между
нейтральными точками источника и приемника возникает напряжение:
называемое напряжением смещения нейтрали.
Из (рис. 7) видно, что при соединении
звездой трехфазная системе представляет
собой электрическую цепь с двумя узлами N
и n. Наиболее удобно определить
напряжение между этими точками методом
узлового напряжения.
73

74.

Чем больше сопротивление нейтрального провода, тем больше величина UnN и
эффективность нейтрального провода уменьшается, т.е. тем больше напряжение фаз
приемника отличается от напряжения фаз источника. Поэтому нейтральный
провод, или его еще называют нулевой, стремятся выполнить с малым
сопротивлением.
В случае обрыва нейтрального провода при несимметричной нагрузке величина
смещения нейтрали UnN будет максимальной. По этой причине в нейтральный
провод не вводят защитных средств, так как при отключении нейтрального
провода на фазах нагрузки могут возникнуть значительные перенапряжения.
74

75. СОЕДИНЕНИЕ ЭЛЕКТРОПРИЕМНИКОВ ТРЕУГОЛЬНИКОМ

Обмотки современных трехфазных генераторов, устанавливаемых на
электростанциях, соединяются всегда звездой.
Приемник соединяют как звездой, так и в треугольник (рис. 10). Условное
обозначение Δ.
СИММЕТРИЧНЫЙ РЕЖИМ
Если сопротивления фаз заданы выражением:
фазные токи определяют по формулам:
75

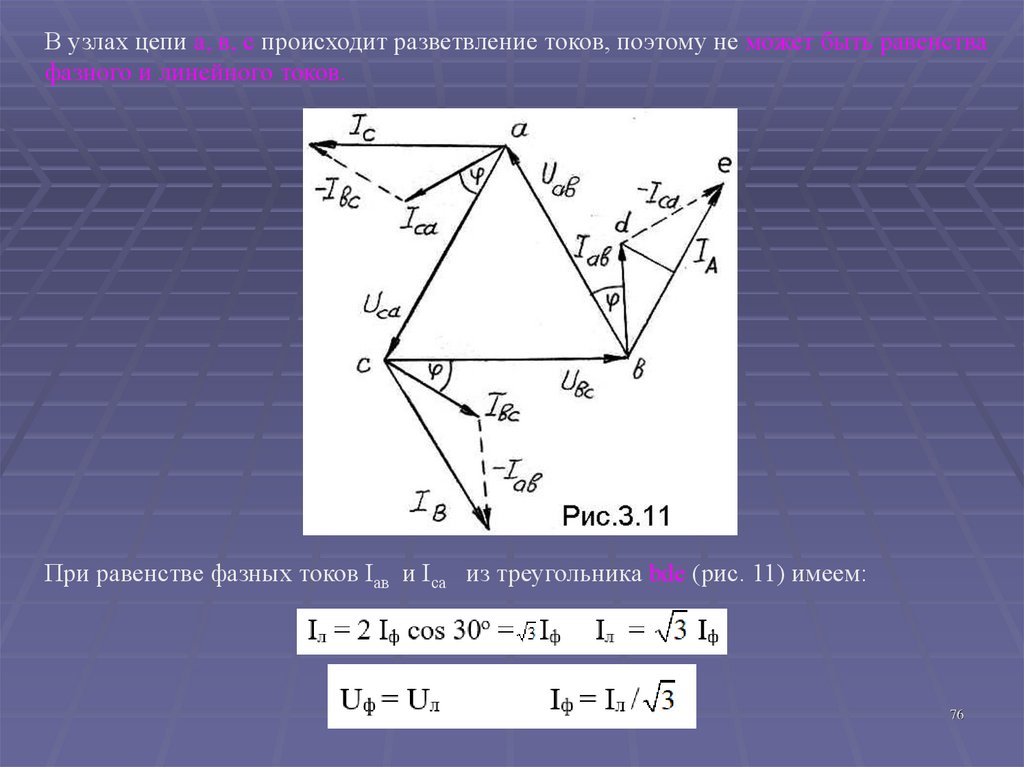
76.

В узлах цепи а, в, с происходит разветвление токов, поэтому не может быть равенства
фазного и линейного токов.
При равенстве фазных токов Iав и Iса из треугольника bdе (рис. 11) имеем:
76

77.

НЕСИММЕТРИЧНЫЙ РЕЖИМ
Зная фазные напряжения, можно найти фазные токи
Линейные токи определяют по фазным токам из уравнений, составленных
согласно первому закону Кирхгофа для узлов a, в, c.
Любой из линейных токов равен геометрической разности соответствующих
векторов токов тех двух фаз приемников, которые соединяются с данным
линейным проводом (рис. 11).
Важной особенностью соединения фаз приемника треугольником является
следующее: при изменении сопротивления одной из фаз режим работы других
фаз остается неизменным, так как линейные напряжения источника являются
постоянными (будет изменяться только ток данной фазы и линейные токи в
проводах линии).
Схема соединения треугольником может быть использована для
включения как симметричной, так и несимметричной нагрузки.
77

78. АВАРИЙНЫЕ РЕЖИМЫ В ТРЕХФАЗНЫХ ЦЕПЯХ

Соединение фаз приемника звездой с нейтральным проводом.
Обрыв фазы
Пусть произойдет обрыв фазы а, тогда ток в этой фазе равен
нулю, Iа = 0, в фазах в и с ток не изменится. Ток в
нейтральном проводе (рис. 12)
Нейтральный провод, по которому протекает ток IN, выравнивает напряжение
на фазах приемника.
78

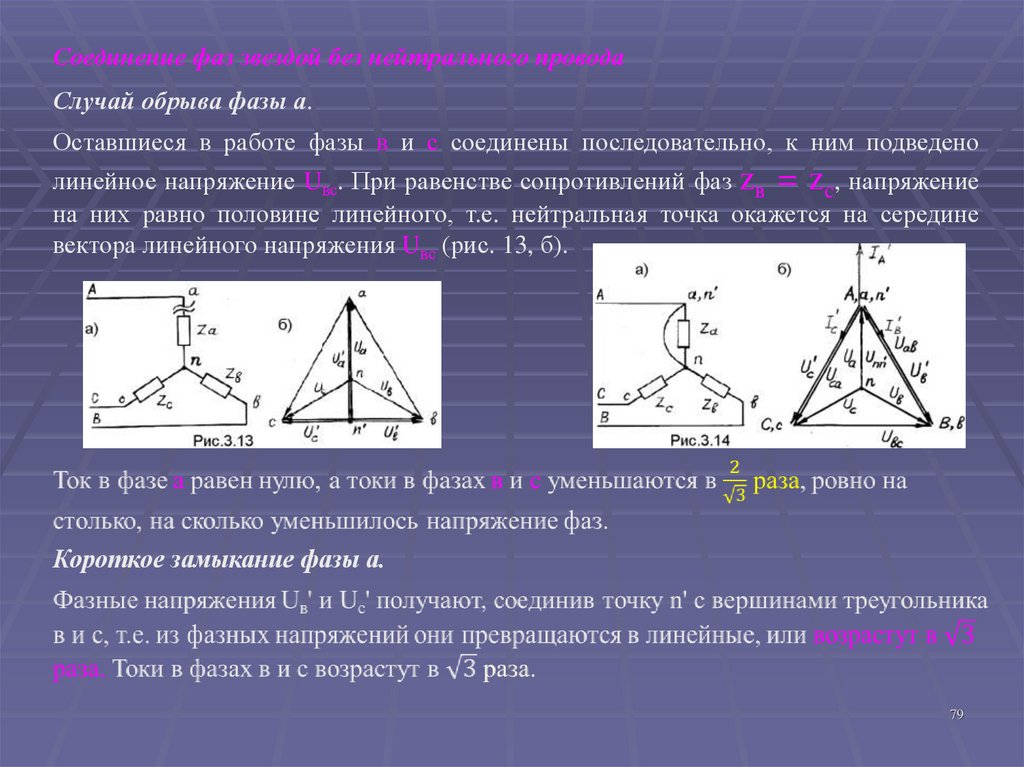
79.

Соединение фаз звездой без нейтрального провода
Случай обрыва фазы а.
Оставшиеся в работе фазы в и с соединены последовательно, к ним подведено
линейное напряжение Uвс. При равенстве сопротивлений фаз zв = zc, напряжение
на них равно половине линейного, т.е. нейтральная точка окажется на середине
вектора линейного напряжения Uвс (рис. 13, б).
Короткое замыкание фазы а.
79

80. Пример 3.

откуда
Из векторной диаграммы (рис.3.14, б) находим, что
80

81. Соединение фаз приемника треугольником

Рассмотрим симметричную активную нагрузку, фазы которой соединены
треугольником. При нормальной работе системы фазных и линейных токов
симметричны.
Обрыв фазы aв (рис. 3.15, а).
Поэтому линейные токи IА и IВ становятся равными фазным токам.
Линейный ток
т.е. определяется так, как это делается в
общем виде, поэтому остается неизменным
(рис.3.15, б).
81

82.

Обрыв линии А.
При обрыве линейного провода А трехфазная цепь преобразуется в однофазную с
фазным напряжением равным линейному, включенному на две параллельные ветви,
в которых в первой ветви сопротивление фазы вc, а во второй последовательно
включенные сопротивления фаз aв и ca (рис.3.16, а).
82

83. МОЩНОСТЬ ТРЕХФАЗНОЙ ЦЕПИ

При соединении фаз приемника звездой:
При соединении фаз приемника треугольником:
Рассмотрим, как изменяется мощность приемника при переключении его фаз со
звезды в треугольник. При соединении фаз приемника треугольником
а при соединении фаз звездой
83

84. Лекция №8 ПЕРЕХОДНЫЕ ПРОЦЕССЫ

Причины возникновения переходных процессов в электрических цепях
Электрические процессы, возникающие в электрической цепи при переходе от
одного установившегося режима к другому, называются переходными.
Переходные процессы могут происходить во
устройствах в следующих случаях:
1) когда включается и выключается источник питания;
2) при возникновении аварийных режимов.
многих
электрических
Физической причиной возникновения переходных процессов в цепях является
наличие в них индуктивных и емкостных элементов. Объясняется это тем, что
энергия магнитного
и электрического
полей этих элементов не может изменяться скачком при коммутации в цепи. Т.е.
они являются инерционными элементами.
В электрических цепях, содержащих только резистивные элементы,
переходные процессы не возникают. В них мгновенно устанавливаются
84
стационарные режимы.

85. Дифференциальные уравнения электрического состояния цепей

Расчет токов и напряжений на участках исследуемой электрической цепи во
время переходного процесса производят, пользуясь уравнениями, составленными в
соответствии с законами Кирхгофа для мгновенных значений токов и напряжений.
Для несложных цепей эту систему уравнений с постоянными параметрами r, L и
С можно представить линейными дифференциальными уравнениями с постоянными
коэффициентами.
При непосредственном интегрировании дифференциальных уравнений
(классический метод) общий интеграл линейных дифференциальных уравнений со
свободным членом (правой частью) получают в результате суммирования частного
решения данного уравнения и общего решения его при равенстве нулю правой части.
Частное решение дифференциального уравнения находят для установившегося
режима, когда переходный процесс закончен. При этом токи и напряжения на участках
цепи определяются параметрами источника энергии и элементов электрической цепи.
Токи и напряжения, которые получаются в результате частного решения для
установившегося режима, называют установившимися (ίу , uу).
Общее решение дифференциального уравнения без правой части соответствует
режиму цепи при отсутствии внешнего источника энергии, т.е. так называемому
свободному режиму. Токи и напряжения, получаемые в результате общего решения
однородного дифференциального уравнения, определяются лишь параметрами
элементов цепи и называются свободными (ίсв, uсв).
85

86.

Суммы установившихся и свободных токов и напряжений определяют
переходные токи и напряжения, т.е. их значения во время переходного процесса
Таким образом расчет переходного процесса классическим методом содержит
следующие этапы:
1. составление системы дифференциальных уравнений цепи и исключение
переменных с целью получения одного дифференциального уравнения для ί или u.
Для простых цепей в качестве искомой величины выбирают либо ток в индуктивном
элементе, либо напряжение на емкостном элементе;
2. составляется общее решение полученного дифференциального уравнения в виде
суммы частного и общего решения дифференциального уравнения;
3. в общем решении следует найти постоянные интегрирования.
Дифференциальные уравнения следует решать при заданных начальных условиях,
которые необходимы для получения однозначного решения
86

87. Законы коммутации

I закон: ток в ветви с индуктивным элементом не может измениться скачком.
В первый момент переходного процесса ток сохраняет то значение, которое он
имел до коммутации.
Докажем это. Пусть в интервале времени от t1 до t2 ток в индуктивном
элементе изменяется от значения ίL(t1) до ίL(t2).
Если интервал времени Δt = t2–t1 стремится к нулю и ίL(t2) ≠ ίL(t1), то средняя
мощность изменения энергии магнитного поля стремится к бесконечности.
II закон: напряжение на емкостном элементе не может измениться скачком.
Этот закон можно получить по аналогии с законом коммутации для индуктивного
элемента.
Действительно, сравнивая WM = Lί2/2
и WЭ = СUc2/2 видим,
что относительно тока (ί) и напряжения (u) они аналогичны. Таким образом,
изменение напряжения на емкостном элементе скачком невозможно, т.е.
87

88.

Ток в индуктивном элементе ίL(0-) и напряжение на емкостном элементе uc(0-)
непосредственно перед коммутацией называются начальными условиями.
Если токи в индуктивных элементах и напряжение на емкостных элементах цепи в
момент времени t- или t(0-) равны нулю, т.е. ίL(0-) = 0 и uc(0-) = 0, то эти условия
называются нулевыми начальными условиями.
88

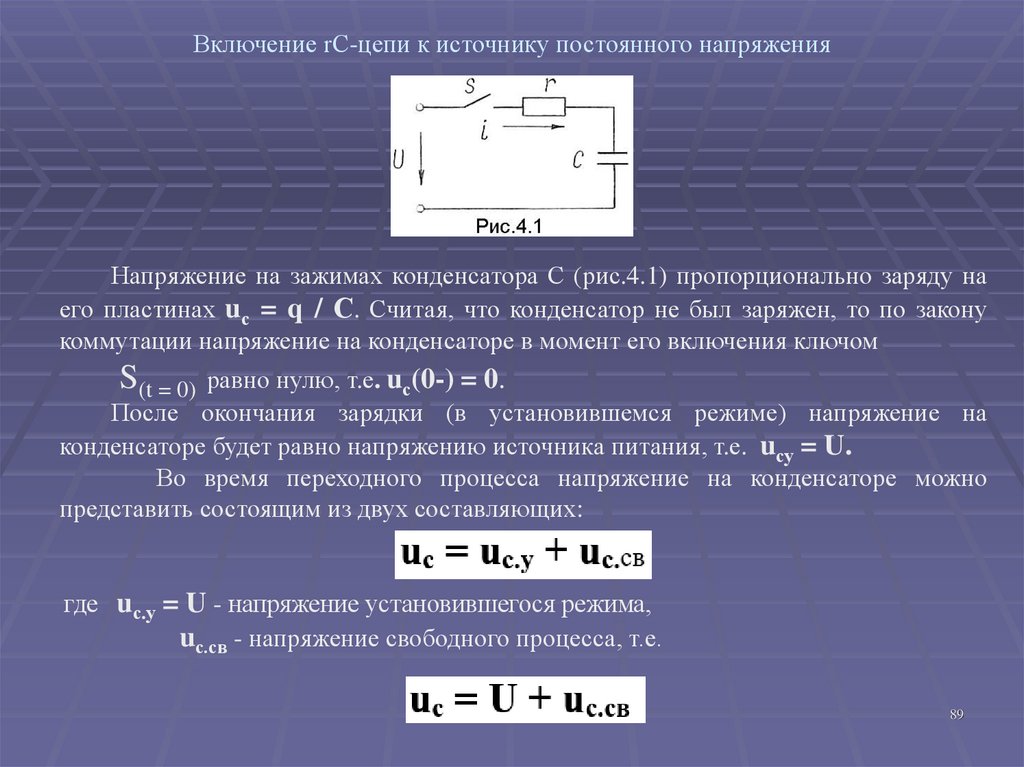
89. Включение rC-цепи к источнику постоянного напряжения

Напряжение на зажимах конденсатора С (рис.4.1) пропорционально заряду на
его пластинах uс = q / С. Считая, что конденсатор не был заряжен, то по закону
коммутации напряжение на конденсаторе в момент его включения ключом
S(t = 0) равно нулю, т.е. uс(0-) = 0.
После окончания зарядки (в установившемся режиме) напряжение на
конденсаторе будет равно напряжению источника питания, т.е. uсу = U.
Во время переходного процесса напряжение на конденсаторе можно
представить состоящим из двух составляющих:
где uс.у = U - напряжение установившегося режима,
uс.св - напряжение свободного процесса, т.е.
89

90.

По второму закону Кирхгофа для rC-цепи (рис.4.1)
Заменив в уравнении ток выражением
получим уравнение
где учтено, что напряжение U постоянное, т.е. dU/dt = 0, или
90

91.

Скорость протекания процесса характеризуют постоянной времени rC- цепи:
чем больше τ, тем медленнее процесс.
Постоянная времени имеет размерность времени, так как
Этому уравнению удовлетворяет решение:
где А - постоянная интегрирования.
Следовательно, в первый момент после замыкания выключателя S при t = 0
напряжение uc (0+), сохраняясь неизменным, будет также равно нулю
откуда U + A = 0 или A = - U.
Таким образом, напряжение на конденсаторе при зарядке
91

92.

т.е. оно равно разности постоянного напряжения U источника питания и свободного
напряжения, убывающего с течением времени по экспоненциальному закону от
значения U до нуля.
Изменение напряжения u показано на рис. 4.2. Ток переходного процесса, или
зарядный ток
Ток от начального значения I с
течением
времени
постепенно
уменьшается
по
экспоненциальному
закону
(рис.4.2). За время t = τ зарядный
ток (15) уменьшается в е = 2,72 раза
напряжение на конденсаторе за то же время
возрастает от 0 до 0,63 U,
92

93.

Падение напряжения на сопротивлении r пропорционально току
При разряде конденсатора емкостью С, заряженного до напряжения
uc = U, на резистор r (рис.4.3) ключ S замкнут.
Уравнение контура по второму закону Кирхгофа
После разрядки конденсатора или в установившемся режиме напряжение на
конденсаторе равно нулю, т.е. Uс.у = 0. Следовательно, Uс = Uс.св
или
Решение этого уравнения записывается в виде
где учтено, что Uс.у = 0.
93

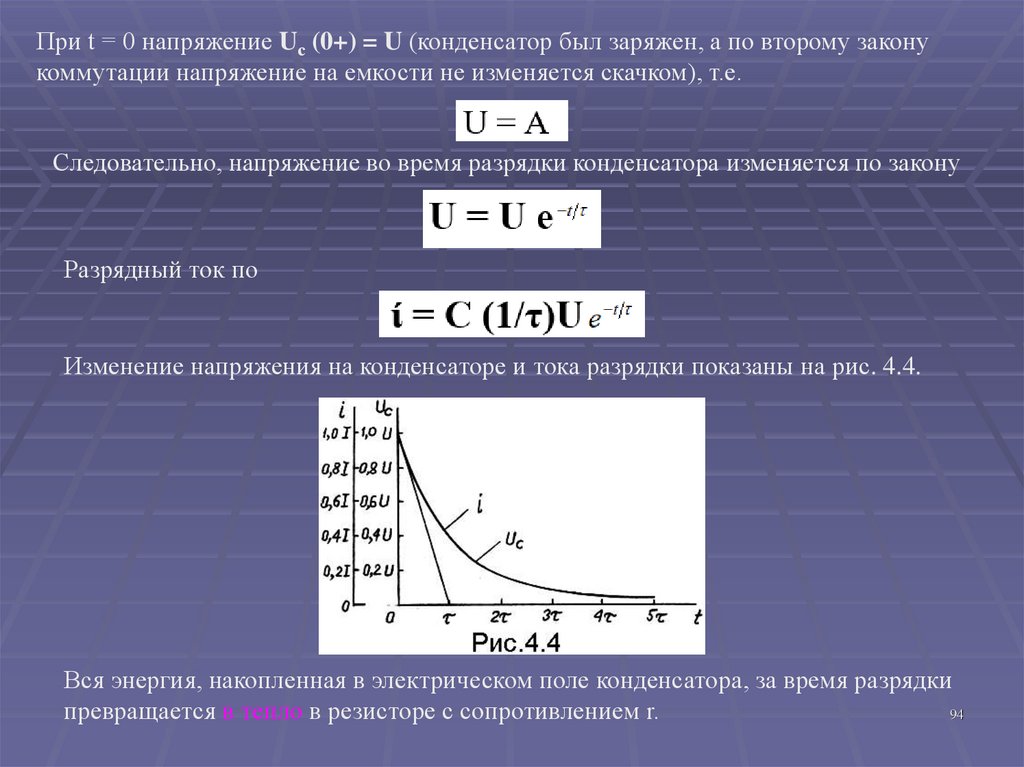
94.

При t = 0 напряжение Uс (0+) = U (конденсатор был заряжен, а по второму закону
коммутации напряжение на емкости не изменяется скачком), т.е.
Следовательно, напряжение во время разрядки конденсатора изменяется по закону
Разрядный ток по
Изменение напряжения на конденсаторе и тока разрядки показаны на рис. 4.4.
Вся энергия, накопленная в электрическом поле конденсатора, за время разрядки
94
превращается в тепло в резисторе с сопротивлением r.

95. Простейший генератор пилообразного напряжения (ГЛИН)

Схема простейшего ГЛИН приведена на рис.4.5, а. В качестве управляющего
элемента используется тиристор. Тиристор обладает тем свойством, что при малых
напряжениях его сопротивление велико, а при определенном напряжении,
называемом напряжением пробоя Uпр, оно скачком уменьшается до очень
незначительного значения. В качестве управляющего элемента могут
использоваться и другие электронные приборы (неоновые и электронные лампы,
транзисторы и т.д.).
95