Лекция 3 Арифметические основы ЭВМ

1.

Лекция 3
Арифметические основы ЭВМ
Халеева Елена Петровна
к.п.н., доцент
1

2.

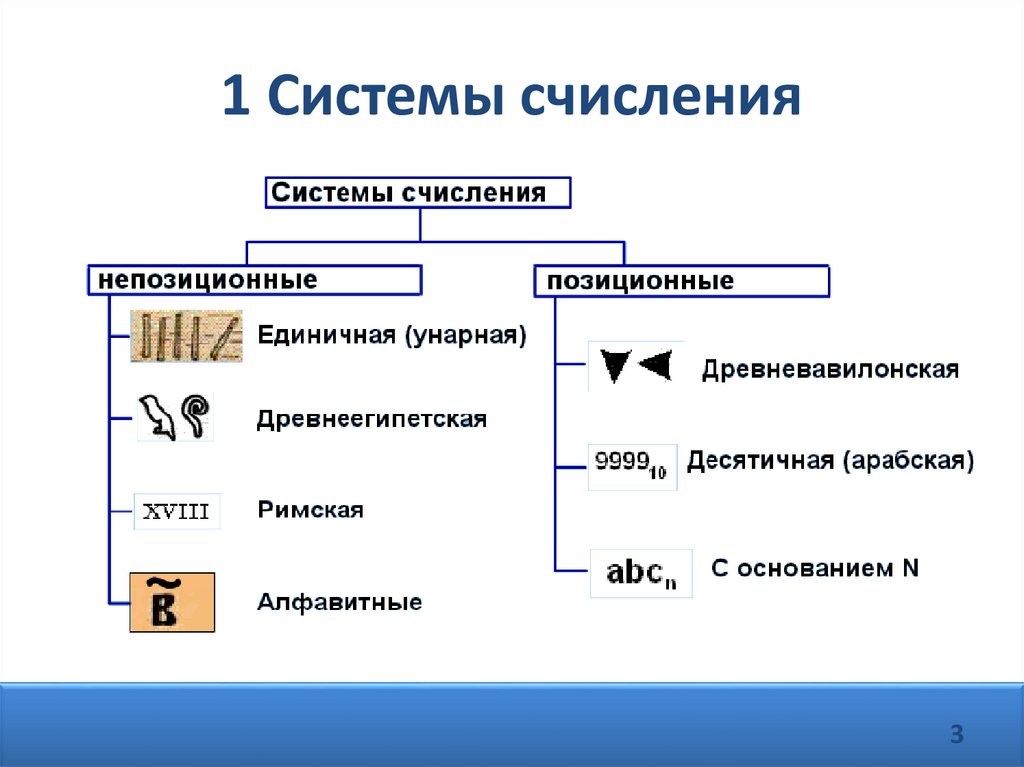
1 Системы счисления
Система счисления – это способ
представления чисел и соответствующие
ему правила действия над числами.
2

3.

1 Системы счисления
3

4.

1 Системы счисления
Примеры:
• Непозиционная
• Позиционная
III
111
4

5.

1 Системы счисления
Примеры:
• Непозиционная
• Позиционная
III
111
• Непозиционная
• Позиционная
IVиVI
15 и 51
5

6.

1 Системы счисления
Место, которое занимает цифра в записи
числа, называют разрядом.
Разряды нумеруются (нулевой, первый,
второй …..) или называются единицы,
десятки, сотни…
6

7.

1 Системы счисления
Цифры, используемые для записи чисел
называется алфавитом системы
счисления.
Объем алфавита определяет основание
системы счисления.
7

8.

1 Системы счисления
8

9.

1 Системы счисления
Для того чтобы перевести десятичное число
A в систему счисления с основанием q
необходимо выполнить последовательное
деление числа A и получаемых неполных
частных на q до тех пор пока не получим частое
меньше q.
Для записи числа в новой системе
счисления, выписываются последнее частное и
полученные остатки от последнего к первому.
9

10.

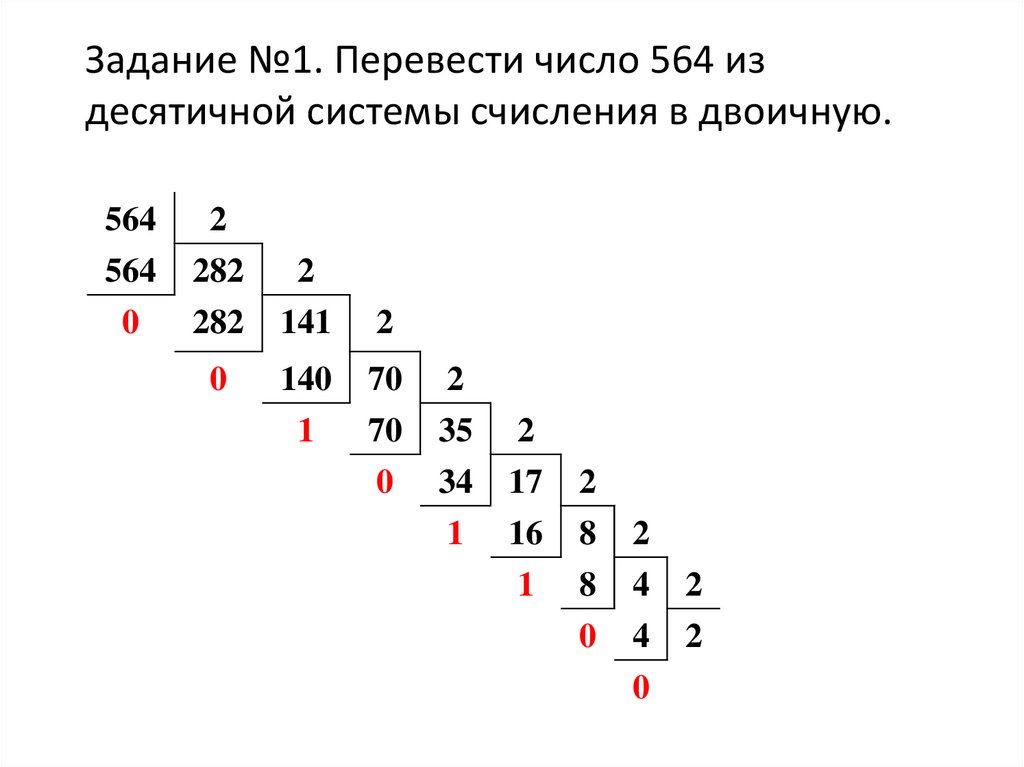
Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
0
2
282
10

11.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
0
2
282
282
2
141
0
11

12.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
0
2
282
282
0
2
141
140
2
70
1
12

13.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
13

14.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
34
1
2
17
14

15.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
34
1
2
17
16
2
8
1
15

16.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
34
1
2
17
16
1
2
8
8
0
2
4
16

17.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
34
1
2
17
16
1
2
8
8
0
2
4
4
0
2
2

18.

Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
564
564
2
282
0
282
0
2
141
140
1
2
70
70
0
2
35
34
1
2
17
16
1
2
8
8
0
2
4
4
0
2
2
2
0
2
1

19.

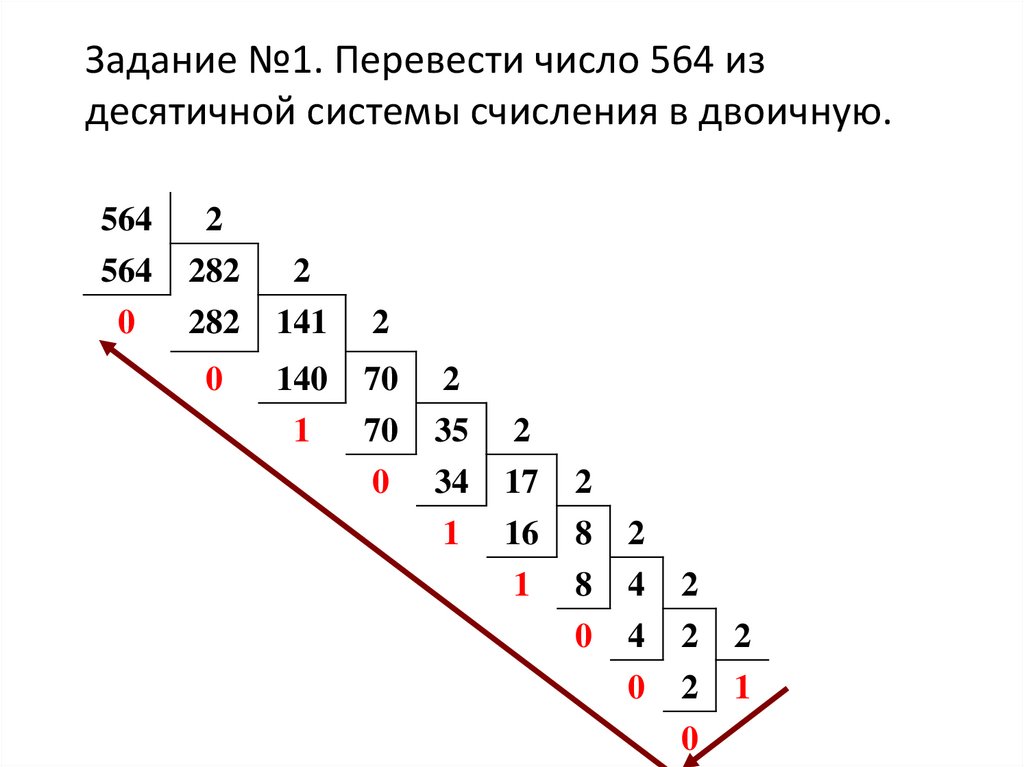
Задание №1. Перевести число 564 из
десятичной системы счисления в двоичную.
Таким образом, получаем равенство
564(10) = 1000110100(2)
Ответ: 1000110100(2)
19

20.

Задание №2. Перевести число 324 из
десятичной системы счисления в двоичную.
20

21.

1 Системы счисления
Развернутой формой записи числа
называется запись в виде
Aq= (an-1qn-1+an-2qn-2+…+a0q0+a-1q-1+a-2q-2+…+a-mq-m),
где Aq – число,
q – основание системы счисления,
ai – цифры данной системы счисления,
n – число разрядов целой части числа,
m – число разрядов дробной части числа
21

22.

Задание №3. Перевести число 10011101(2) из
двоичной системы счисления в десятичную.
Решение
10011101(2) = 1·27 + 0·26 + 0·25 + 1·24 + 1·23 + 1·22 +
+ 0·21 + 1·20 = 128 + 16 + 8 + 4 + 1 = 157(10).
Ответ: 157(10).
Ответ: 51830(10).
22

23.

Задание №4. Перевести число 11100101(2) из
двоичной системы счисления в десятичную.
Ответ: 51830(10).
23

24.

2 Двоичная арифметика
Таблица сложения в
двоичной системе
счисления
0+0=0
Таблица умножения в
двоичной системе
счисления
0·0=0
0+1=1
1+0=1
1+1=10
0·1=0
1·0=0
1·1=1
24

25.

2 Двоичная арифметика
Задание №5. Найти сумму двоичных чисел
10000000100(2) и 111000010(2).
Решение
Сложение проще всего выполнять в столбик,
записывая, как и в десятичной системе,
разряды второго числа под
соответствующими разрядами первого.
1 0 1 0 1 0 0 0 1 0 0
+
1 1 1 0 0 0 0 1 0
1 1 1 0 0 0 0 0 1 1 0
2525

26.

2 Двоичная арифметика
Задание №5. Найти сумму двоичных чисел
10000000100(2) и 111000010(2).
Решение
Сложение проще всего выполнять в столбик,
записывая, как и в десятичной системе,
разряды второго числа под соответствующими
разрядами первого.
1 0 0 0 0 0 0 0 1 0 0
+
1 1 1 0 0 0 0 1 0
1 0 1 1 1 0 0 0 1 1 0
2626

27.

2 Двоичная арифметика
Задание №6. Найти сумму двоичных чисел
11100100100(2) и 110001010(2).
2727

28.

2 Двоичная арифметика
Задание №7. Найти разность двоичных чисел
10010110(2) и 1101011(2).
Решение
0
–
1
1
0
1
10 0
0
1
1
0
1
0
10 0
0
1
1
0
1
0
10 10
1
0
1
1
1
1
2828

29.

2 Двоичная арифметика
Задание №7. Найти разность двоичных чисел
10010110(2) и 1101011(2).
Решение
0
–
1
1
0
1
0
0
1
1
1
0
0
0
0
1
1
1
0
0
0
1
1
1
0
1
1
2929

30.

2 Двоичная арифметика
Задание №8. Найти разность двоичных чисел
11100010(2) и 1001110(2).
3030

31.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
1
0
0
1
0
1
1
1
0
1
1
1
1
1
1
1
0
1
1
1
0
1
0
0
1
0
0
0
0
0
1
1
1
0
0
0
1
1
0
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
0
1
4=100
3=11
3131

32.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
1
0
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
3232

33.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
1
1
0
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
3333

34.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
1
1
0
1
0
1
0
0
0
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3434

35.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
0
0
1
1
1
1
1
0
1
1
0
1
0
0
0
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3535

36.

2 Двоичная арифметика
Задание №9. Найти произведение чисел
100111(2) и 1000111(2).
Решение
×
1
1
0
0
0
1
1
0
1
1
1
1
1
0
1
1
1
0
1
0
0
0
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
0
0
1
3636

37.

2 Двоичная арифметика
Задание №10. Найти произведение чисел
100001(2) и 10111(2).
3737

38.

3 Кодирование чисел
• Целое число
– Прямой
– Обратный
– Дополнительный
• Дробное число
– Нормализованный
3838

39.

3 Кодирование чисел
• Прямой код
Для получения прямого кода числа нужно
дополнить слева двоичную запись таким
количеством незначащих нулей, сколько
требует заданный тип.
Первая левая цифра кодирует знак числа:
0 – положительное, 1 – отрицательное.
3939

40.

3 Кодирование чисел
• Обратный код
Обратный и дополнительный код находят
для отрицательного числа.
Для получения обратного кода инвертируют
все цифры прямого кода, за исключением
знакового разряда.
4040

41.

3 Кодирование чисел
• Дополнительный код
Прибавив к обратному коду 1, получают
дополнительный код отрицательного
числа.
4141

42.

3 Кодирование чисел
Задание №11. Представить в прямом,
обратном и дополнительном кодах
формата Integer (16 бит) число (-45).
4242

43.

3 Кодирование чисел
Решение
1. Переведем данное число в двоичную
систему счисления.
45(10) = 101101(2).
2. Запишем прямой код числа (–45):
[–4510]пр = 1’000000000101101 – тип Integer.
4343

44.

3 Кодирование чисел
3. Для получения обратного кода
инвертируем все цифры прямого кода, за
исключением знакового разряда.
[–4510]обр = 1’111111111010010 – тип Integer.
4444

45.

3 Кодирование чисел
4. Прибавив к обратному коду 1, получим
дополнительный код отрицательного
числа.
[–4510]доп = 1’111111111010011 – тип Integer.
4545

46.

3 Кодирование чисел
Задание №12. Представить в прямом,
обратном и дополнительном кодах
формата Integer (16 бит) число (-113).
4646

47.

3 Кодирование чисел
Задание №13. Представить в прямом,
обратном и дополнительном кодах
формата Integer (16 бит) число 59.
4747

48.

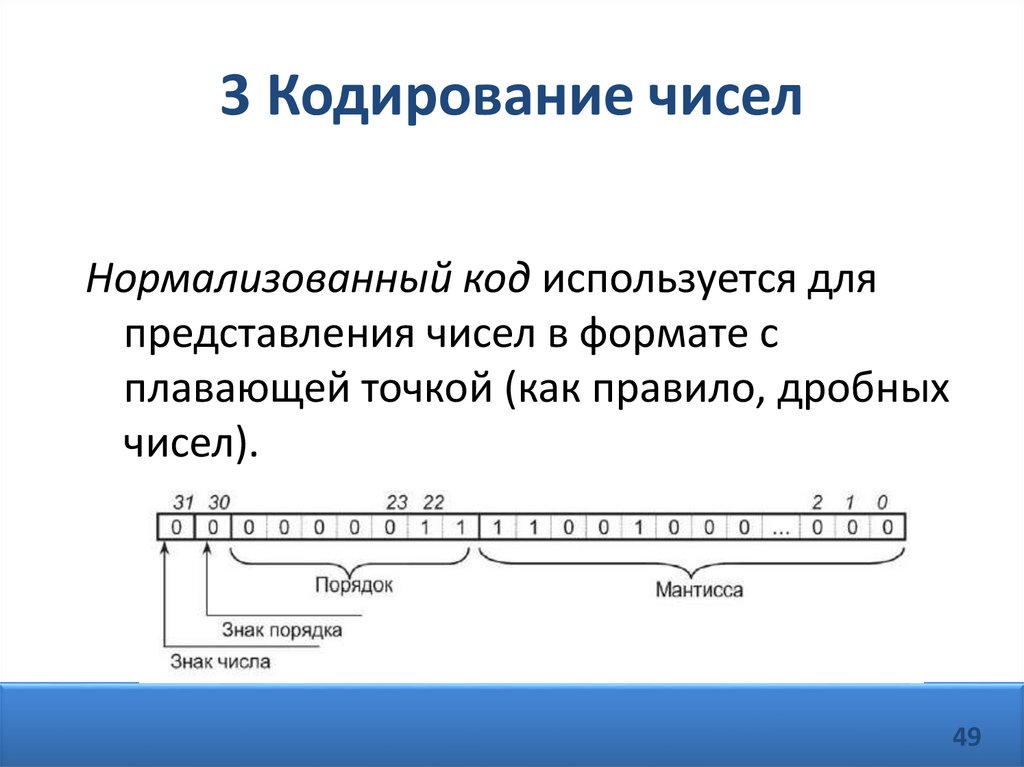
3 Кодирование чисел
Нормализованный код используется для
представления чисел в формате с
плавающей точкой (как правило, дробных
чисел).
4848

49.

3 Кодирование чисел
Нормализованный код используется для
представления чисел в формате с
плавающей точкой (как правило, дробных
чисел).
4949

50.

3 Кодирование чисел
5050

51.

3 Кодирование чисел
Задание №14. Представить в
нормализованном коде (32 бита)
число 15,25.
Решение
5151

52.

3 Кодирование чисел
Задание №14. Представить в
нормализованном коде (32 бита)
число -15,25.
Решение
1. Переводим число в двоичную систему
счисления:
15,25 (10) = 1111.01(2)
5252

53.

3 Кодирование чисел
Задание №14. Представить в
нормализованном коде (32 бита)
число -15,25.
Решение
2. Выполним нормализацию:
15,25 (10) = 1,11101(2) е3
Мантисса: 11101
5353

54.

3 Кодирование чисел
Задание №14. Представить в
нормализованном коде (32 бита)
число -15,25.
Решение
3. Вычислим машинный порядок:
3 + 127 = 130
130(10) = 10000010
5454

55.

3 Кодирование чисел
Задание №14. Представить в
нормализованном коде (32 бита)
число -15,25.
Решение
4. Запишем код числа:
31
30
23
22
0
1 1 0 0 0 0 0 1 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
порядок
мантисса
5555

56.

3 Кодирование чисел
Задание №15. Представить в
нормализованном коде (32 бита)
число 264,125.
5656

57.

3 Кодирование чисел
Задание №15. Представить в
нормализованном коде (32 бита)
число -45,1225
5757